C++数据结构笔记(10)递归实现二叉树的三序遍历
对于三种遍历方式来说,均为先左后右!区别在于根结点的位置顺序
先序遍历:根——左——右
中序遍历:左——根——右
后序遍历:左——右——根
(所谓先中后的顺序,是指根结点D先于子树还是后于子树出现)
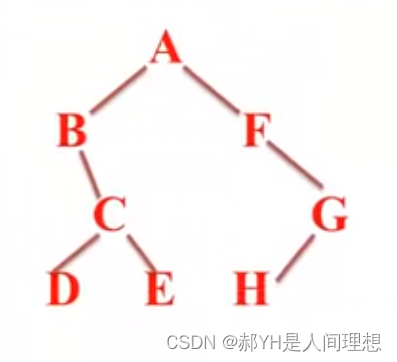
如上图:
先序遍历的结果为:A B C D E F G H
中序遍历的结果为:B D C E A F H G
后序遍历的结果为:D E C B H G F A
定义树的结点类型
typedef struct BinaryNode{char ch;struct BinaryNode* lchild;struct BinaryNode* rchild;
}BinaryNode;根据图例创建二叉树
void CreateBinaryTree()
{//创建结点 BinaryNode node1={'A',NULL,NULL};BinaryNode node2={'B',NULL,NULL};BinaryNode node3={'C',NULL,NULL};BinaryNode node4={'D',NULL,NULL};BinaryNode node5={'E',NULL,NULL};BinaryNode node6={'F',NULL,NULL};BinaryNode node7={'G',NULL,NULL};BinaryNode node8={'H',NULL,NULL};//创建结点关系node1.lchild=&node2;node1.rchild=&node6;node2.rchild=&node3;node3.lchild=&node4;node3.rchild=&node5;node6.rchild=&node7;node7.lchild=&node8;
}递归实现先序遍历
void RecursionFirst(BinaryNode* root)
{ if(root==NULL)//遍历到空结点return;cout<<(root->ch)<<" "; //输出根结点RecursionFirst(root->lchild);//要点:虽然一左一右看似连在一起,其实是将首个根结点的左子树全部遍历完毕,才会去遍历右子树 RecursionFirst(root->rchild);//先序遍历的顺序为:根-左-右
}
递归实现中序遍历
void RecursionMiddle(BinaryNode* root)
{if(root==NULL)return;RecursionMiddle(root->lchild);cout<<(root->ch)<<" "; RecursionMiddle(root->rchild);//中序遍历的顺序为:左-根-右
}递归实现后序遍历
void RecursionLast(BinaryNode* root)
{if(root==NULL)return;RecursionLast(root->lchild);RecursionLast(root->rchild);cout<<(root->ch)<<" "; //后序遍历的顺序为:左-右-根
}在CreateBinaryTree方法中添加函数调用
//遍历结点cout<<"先序遍历:"<<endl; RecursionFirst(&node1); cout<<endl; cout<<"中序遍历:"<<endl; RecursionMiddle(&node1);cout<<endl; cout<<"后序遍历:"<<endl; RecursionLast(&node1);cout<<endl; 头文件及主函数
int main(int argc, char** argv) {CreateBinaryTree();//主函数只负责调用即可 return 0;
}运行结果如下:与结果相一致
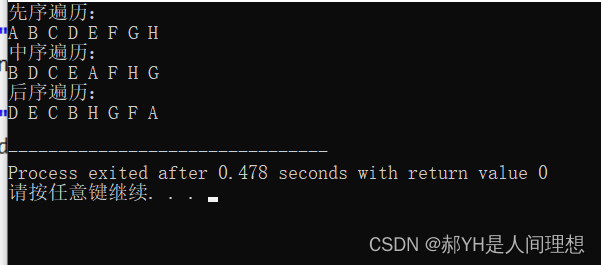
相关文章:

C++数据结构笔记(10)递归实现二叉树的三序遍历
对于三种遍历方式来说,均为先左后右!区别在于根结点的位置顺序 先序遍历:根——左——右 中序遍历:左——根——右 后序遍历:左——右——根 (所谓先中后的顺序,是指根结点D先于子树还是后于…...
hMailServer-5.3.3-B1879.exe
hMailServer-5.3.3-B1879.exe...

后端校验JSR303
目录 一、导入依赖 二、实现步骤 三、分组校验 四、自定义校验 一、导入依赖 <dependency><groupId>javax.validation</groupId><artifactId>validation-api</artifactId><version>2.0.1.Final</version></dependency> 二…...

vmware磁盘组使用率100%处理
今天在外办事时,有客户发过来一个截图,问vmware 磁盘组空间使用率100%咋办?如下图: 直接回复: 1、首先删除iso文件等 2、若不存在ISO文件等,找个最不重要的虚拟机直接删除,删除后稍等就会释放…...
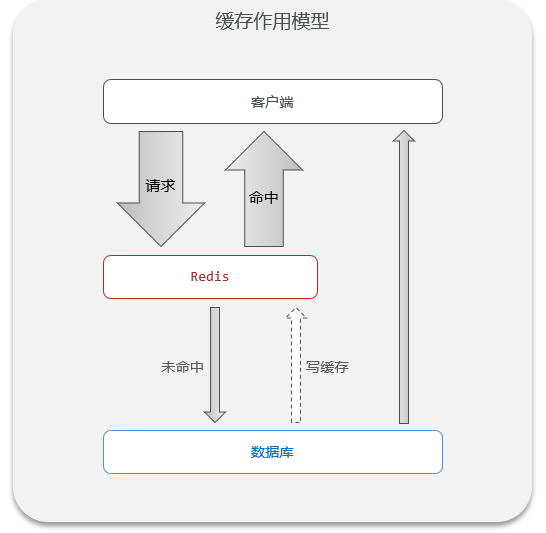
Redis实战(3)——缓存模型与缓存更新策略
1 什么是缓存? 缓存就是数据交换的缓冲区, 是存贮数据的临时区,一般读写性能较高 \textcolor{red}{是存贮数据的临时区,一般读写性能较高} 是存贮数据的临时区,一般读写性能较高。缓存可在多个场景下使用 以一次 w e b 请求为例…...

python与深度学习(十):CNN和cifar10二
目录 1. 说明2. cifar10的CNN模型测试2.1 导入相关库2.2 加载数据和模型2.3 设置保存图片的路径2.4 加载图片2.5 图片预处理2.6 对图片进行预测2.7 显示图片 3. 完整代码和显示结果4. 多张图片进行测试的完整代码以及结果 1. 说明 本篇文章是对上篇文章训练的模型进行测试。首…...
剑指offer12 矩阵中的路径 13 机器人的运动范围 34.二叉树中和为某一值得路径
class Solution { public:bool exist(vector<vector<char>>& board, string word) {int rowboard.size(),colboard[0].size();int index0,i0,j0;if(word.size()>row*col) return 0;//vector<vector<int>> visit[row][col];//标记当前位置有没有…...

Pushgateway+Prometheus监控Flink
思路方案 FlinkMtrics->pushgateway->prometheus->grafnana->altermanager 方案 : Flink任务先将数据推到pushgateway。然后pushgateway将值推送到prometheus,最后grafana展示prometheus中的值, 去这个 https://prometheus.io/download/ 下载最新的 Prometheu…...
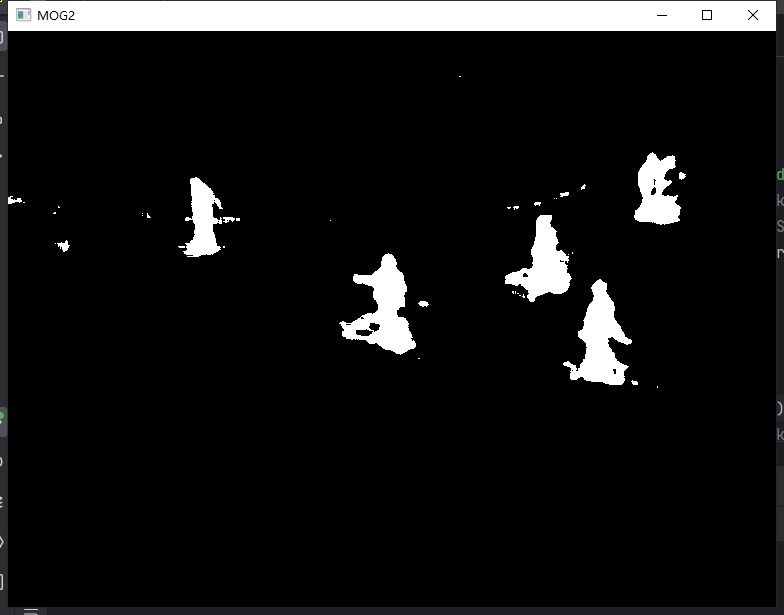
OpenCV图像处理-视频分割静态背景-MOG/MOG2/GMG
视频分割背景 1.概念介绍2. 函数介绍MOG算法MOG2算法GMG算法 原视频获取链接 1.概念介绍 视频背景扣除原理:视频是一组连续的帧(一幅幅图组成),帧与帧之间关系密切(GOP/group of picture),在GOP中,背景几乎…...

nginx 反向代理浅谈
前言 通常情况下,客户端向Web服务器发送请求,Web服务器响应请求并返回数据。而在反向代理中,客户端的请求不直接发送到Web服务器,而是发送到反向代理服务器。反向代理服务器会将请求转发给真实的Web服务器,Web服务器响…...
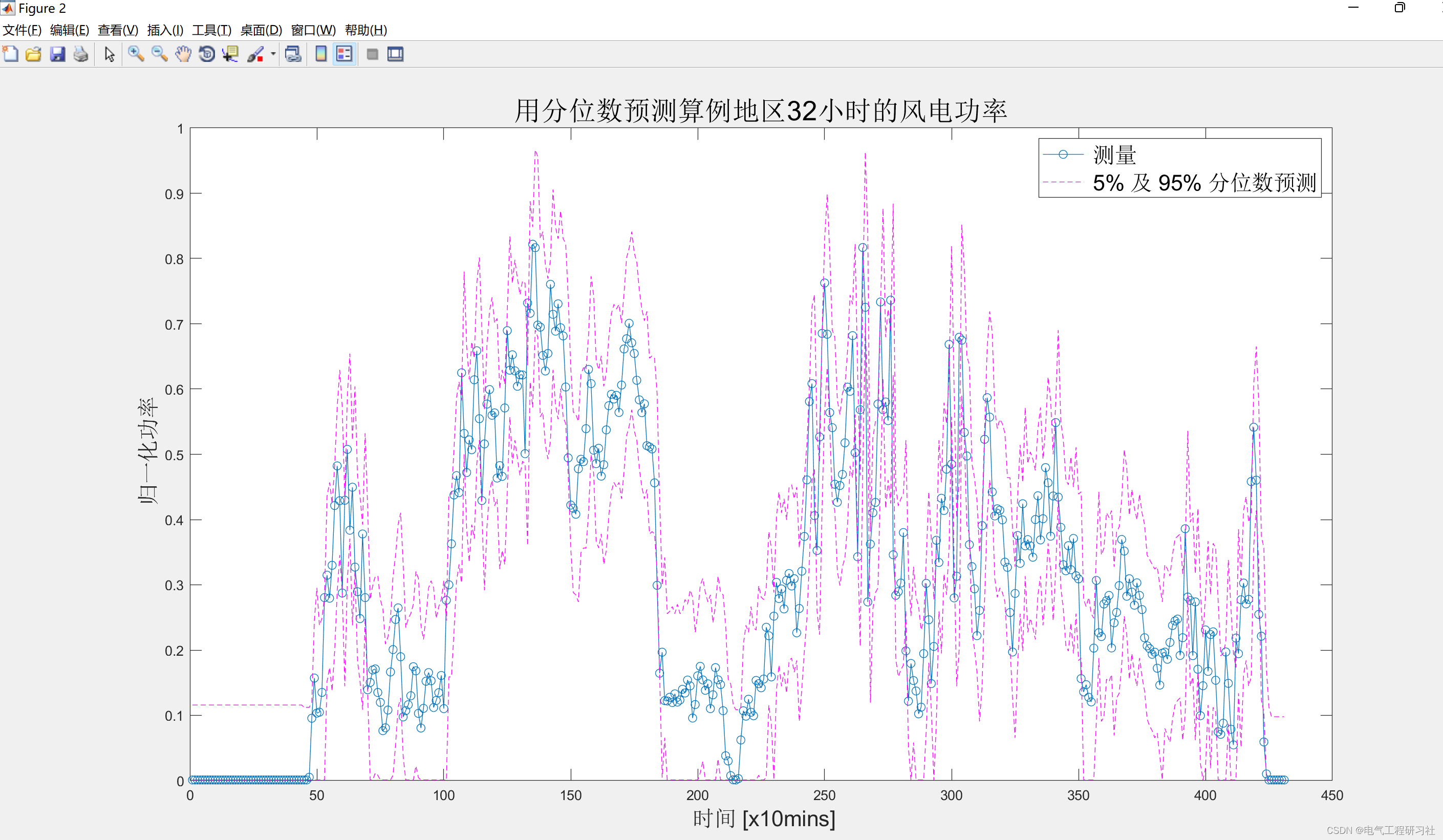
【概率预测】对风力发电进行短期概率预测的分析研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

原型设计模式go实现尝试
文章目录 前言代码结果总结 前言 本文章尝试使用go实现“原型”。 代码 package mainimport ("fmt" )// 不同原型标志枚举 type Type intconst (PROTOTYPE_1 Type iotaPROTOTYPE_2 )// 原型接口 type IPrototype interface {Clone() IPrototypeMethod(value int)P…...
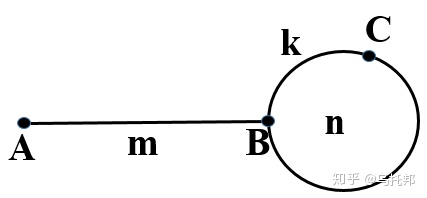
链表是否有环、环长度、环起点
问题引入 如何检测一个链表是否有环,如果有,那么如何确定环的长度及起点。 引自博客:上述问题是一个经典问题,经常会在面试中被问到。我之前在杭州一家网络公司的电话面试中就很不巧的问到,当时是第一次遇到那个问题&…...

有效文档管理离不开这几个特点
在我们日常生活中经常会遇到各式各样的文档类型,想要把它们都统一管理起来也不是一件容易的事情。后来looklook就去研究怎么样可以把这一堆文档整理起来呢?接下来,looklook就从有效的文档管理展开,和大家分享一下! 有效…...

爬虫-requests-cookie登录古诗文网
一、前言 1、requests简介 requests是一个很实用的Python HTTP客户端库,爬虫和测试服务器响应数据时经常会用到,它是python语言的第三方的库,专门用于发送HTTP请求,使用起来比urllib更简洁也更强大。 2、requests的安装 pip i…...
Spring Boot实践三 --数据库
一,使用JdbcTemplate访问MySQL数据库 1,确认本地已正确安装mysql 按【winr】快捷键打开运行;输入services.msc,点击【确定】;在打开的服务列表中查找mysql服务,如果没有mysql服务,说明本机没有…...
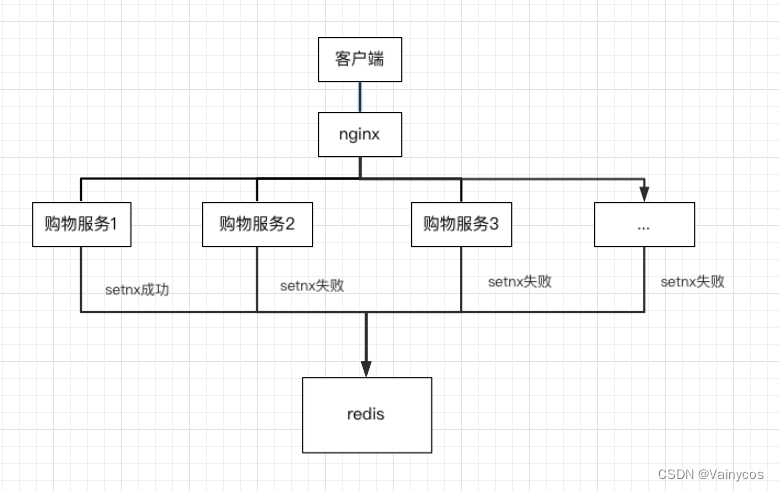
分布式锁漫谈
简单解释一下个人理解的分布式锁以及主要的实现手段。 文章目录 什么是分布式锁常用分布式锁实现 什么是分布式锁 以java应用举例,如果是单应用的情况下,我们通常使用synchronized或者lock进行线程锁,主要为了解决多线程或者高并发场景下的共…...
mac 安装 php 与 hyperf 框架依赖的扩展并启动 gptlink 项目
m系列 mac 安装 php 与 hyperf 框架依赖的扩展并启动 gptlink 项目 gptlink 项目是一个前后端一体化的 chatgpt 开源项目 gptlink 项目地址:https://github.com/gptlink/gptlink 安装 php 8.0 版本: brew install php8.0安装完成后提示如下ÿ…...

ansible中run_once的详细介绍和使用说明
在Ansible中,run_once是一个用于控制任务在主机组中只执行一次的关键字参数。当我们在编写Ansible任务时,有时候我们希望某个任务只在主机组中的某个主机上执行一次,而不是在每个主机上都执行。 以下是run_once参数的详细说明和用法…...
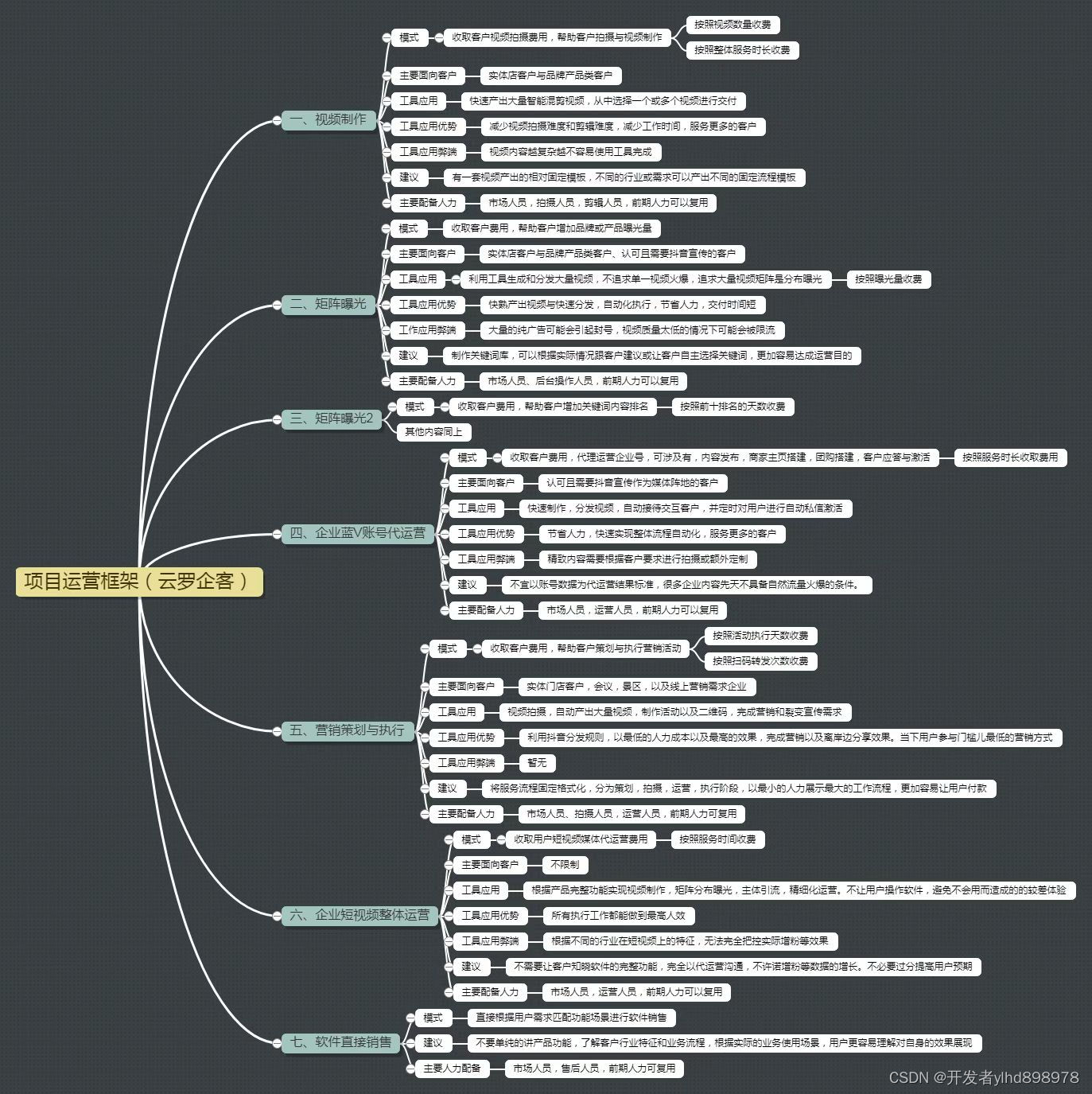
短视频矩阵系统源码开发流程
一、视频矩阵系统源码开发流程分为以下几个步骤: 四、技术开发说明: 产品原型PRD需求文档产品交互流程图部署方式说明完整源代码源码编译方式说明三方框架和SDK使用情况说明和代码位置平台操作文档程序架构文档 一、抖音SEO矩阵系统源码开发流程分为以…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...

【题解-洛谷】P10480 可达性统计
题目:P10480 可达性统计 题目描述 给定一张 N N N 个点 M M M 条边的有向无环图,分别统计从每个点出发能够到达的点的数量。 输入格式 第一行两个整数 N , M N,M N,M,接下来 M M M 行每行两个整数 x , y x,y x,y,表示从 …...

SFTrack:面向警务无人机的自适应多目标跟踪算法——突破小尺度高速运动目标的追踪瓶颈
【导读】 本文针对无人机(UAV)视频中目标尺寸小、运动快导致的多目标跟踪难题,提出一种更简单高效的方法。核心创新在于从低置信度检测启动跟踪(贴合无人机场景特性),并改进传统外观匹配算法以关联此类检测…...

链结构与工作量证明7️⃣:用 Go 实现比特币的核心机制
链结构与工作量证明:用 Go 实现比特币的核心机制 如果你用 Go 写过区块、算过哈希,也大致理解了非对称加密、数据序列化这些“硬核知识”,那么恭喜你,现在我们终于可以把这些拼成一条完整的“区块链”。 不过别急,这一节我们重点搞懂两件事: 区块之间是怎么连接成“链”…...
