LeetCode 436. Find Right Interval【排序,二分;双指针,莫队】中等
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库:https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
给你一个区间数组 intervals ,其中 intervals[i] = [starti, endi] ,且每个 starti 都 不同 。
区间 i 的 右侧区间 可以记作区间 j ,并满足 startj >= endi ,且 startj 最小化 。注意 i 可能等于 j 。
返回一个由每个区间 i 的 右侧区间 在 intervals 中对应下标组成的数组。如果某个区间 i 不存在对应的 右侧区间 ,则下标 i 处的值设为 -1 。
示例 1:
输入:intervals = [[1,2]]
输出:[-1]
解释:集合中只有一个区间,所以输出-1。
示例 2:
输入:intervals = [[3,4],[2,3],[1,2]]
输出:[-1,0,1]
解释:对于 [3,4] ,没有满足条件的“右侧”区间。
对于 [2,3] ,区间[3,4]具有最小的“右”起点;
对于 [1,2] ,区间[2,3]具有最小的“右”起点。
示例 3:
输入:intervals = [[1,4],[2,3],[3,4]]
输出:[-1,2,-1]
解释:对于区间 [1,4] 和 [3,4] ,没有满足条件的“右侧”区间。
对于 [2,3] ,区间 [3,4] 有最小的“右”起点。
提示:
1 <= intervals.length <= 2 * 10^4intervals[i].length == 2-10^6 <= starti <= endi <= 10^6- 每个间隔的起点都 不相同
解法1 排序+二分
最简单的解决方案是对于集合中的每个区间,我们扫描所有区间找到其起点大于当前区间的终点的区间(具有最小差值),时间复杂度为 O ( n 2 ) O(n^2) O(n2) ,在此不详细描述。
对于一个特定的 i t s [ i ] its[i] its[i] 而言,其右端点固定,并且我们只关心目标位置的左端点。
- 首先将每个 i t s [ i ] [ 0 ] its[i][0] its[i][0] 与其对应的索引 i i i 存储在数组 i t s S t a r t itsStart itsStart 中,并对其按 i t s [ i ] [ 0 ] its[i][0] its[i][0] 的大小进行排序;
- 然后枚举每个区间 i t s [ i ] its[i] its[i] 的右端点 i t s [ i ] [ 1 ] its[i][1] its[i][1],利用二分查找在 i t s S t a r t itsStart itsStart 中找到大于等于 i t s [ i ] [ 1 ] its[i][1] its[i][1] 的最小值 v a l val val ,此时区间 i t s [ i ] its[i] its[i] 对应的右侧区间即为 v a l val val 对应的索引。
class Solution {
public:vector<int> findRightInterval(vector<vector<int>>& intervals) {int n = intervals.size();vector<pair<int, int>> itsStart;for (int i = 0; i < n; ++i) itsStart.emplace_back(intervals[i][0], i);sort(itsStart.begin(), itsStart.end());vector<int> ans(n);for (int i = 0; i < n; ++i) {int l = 0, r = n;while (l < r) {int mid = (l + r) >> 1;if (itsStart[mid].first >= intervals[i][1]) r = mid;else l = mid + 1;}ans[i] = l == n ? -1 : itsStart[l].second;}return ans;}
};
复杂度分析:
- 时间复杂度: O ( n log n ) O(n \log n) O(nlogn),其中 n n n 为区间数组的长度。排序的时间为 O ( n log n ) O(n \log n) O(nlogn),每次进行二分查找花费的时间为 O ( log n ) O(\log n) O(logn),一共需要进行 n n n 次二分查找,因此总的时间复杂度为 O ( n log n ) O(n \log n) O(nlogn) 。
- 空间复杂度: O ( n ) O(n) O(n),其中 n n n 为区间数组的长度。 i t s S t a r t itsStart itsStart 一共存储了 n n n 个元素,因此空间复杂度为 O ( n ) O(n) O(n)。
解法2 排序+双指针(莫队思想)
更进一步,在解法一中我们并没有对求解询问的顺序进行调整,这导致了我们不得不每次都在整个左端点序列中进行二分。朴素处理询问的方式,需要每次对整个序列进行双重扫描,复杂度为 O ( n 2 ) O(n^2) O(n2) 。
但实际上,如果我们按照「右端点从小到大」的顺序处理询问,其每个询问对应的「最右区间的左端点」也具有单调特性。具体进行说明。
开辟两个新的数组:
- s t a r t I n t e r v a l s startIntervals startIntervals,基于所有区间的起始点和下标从小到大排序。
- e n d I n t e r v a l s endIntervals endIntervals,基于所有区间的结束点和下标从小到大排序。
我们从 e n d I n t e r v a l s endIntervals endIntervals 数组中取出第 i i i 个区间,从左到右扫描 s t a r t I n t e r v a l s startIntervals startIntervals 数组中的区间起点来找到满足右区间条件的区间。设 e n d I n t e r v a l s endIntervals endIntervals 数组中第 i i i 个元素的右区间为 s t a r t I n t e r v a l s startIntervals startIntervals 数组中的第 j j j 个元素,此时可以知道:
startIntervals [ j − 1 ] [ 0 ] < endIntervals [ i ] [ 0 ] , startIntervals [ j ] [ 0 ] ≥ endIntervals [ i ] [ 0 ] \begin{aligned} \textit{startIntervals}[j-1][0] < \textit{endIntervals}[i][0],\\ \textit{startIntervals}[j][0] \ge \textit{endIntervals}[i][0] \end{aligned} startIntervals[j−1][0]<endIntervals[i][0],startIntervals[j][0]≥endIntervals[i][0]
当我们遍历 e n d I n t e r v a l s endIntervals endIntervals 数组中第 i + 1 i+1 i+1 个元素时,不需要从第一个索引开始扫描 s t a r t I n t e r v a l s startIntervals startIntervals 数组,可以直接从第 j j j 个元素开始扫描 s t a r t I n t e r v a l s startIntervals startIntervals 数组。由于数组中所有的元素都是已排序,因此可以知道
startIntervals [ j − 1 ] [ 0 ] < endIntervals [ i ] [ 0 ] ≤ endIntervals [ i + 1 ] [ 1 ] \textit{startIntervals}[j-1][0] < \textit{endIntervals}[i][0] \le \textit{endIntervals}[i+1][1] startIntervals[j−1][0]<endIntervals[i][0]≤endIntervals[i+1][1]
所以数组 s t a r t I n t e r v a l s startIntervals startIntervals 的前 j − 1 j−1 j−1 的元素的起始点都小于 e n d I n t e r v a l s [ i + 1 ] [ 1 ] endIntervals[i+1][1] endIntervals[i+1][1] ,因此可以直接跳过前 j − 1 j-1 j−1 个元素,只需要从 j j j 开始搜索即可。
因此,我们可以运用莫队思想:通过调整询问的处理顺序,来减少扫描目标位置的指针移动次数。将其从「必然进行 n 2 n^2 n2 次移动」优化为「最多不超过 n n n 次移动」,从而将 构造答案 的复杂度从 O ( n 2 ) O(n^2) O(n2) 优化为 O ( n ) O(n) O(n) 。
最后,由于每个 i n t e r v a l s [ i ] intervals[i] intervals[i] 只关心目标位置的「左端点」,因此我们无须对某一端进行分块,而直接使用双指针实现即可。
class Solution {
public:vector<int> findRightInterval(vector<vector<int>>& intervals) {vector<pair<int, int>> startIntervals;vector<pair<int, int>> endIntervals;int n = intervals.size();for (int i = 0; i < n; i++) {startIntervals.emplace_back(intervals[i][0], i);endIntervals.emplace_back(intervals[i][1], i);}sort(startIntervals.begin(), startIntervals.end());sort(endIntervals.begin(), endIntervals.end());vector<int> ans(n, -1);for (int i = 0, j = 0; i < n && j < n; i++) {while (j < n && endIntervals[i].first > startIntervals[j].first)j++;if (j < n)ans[endIntervals[i].second] = startIntervals[j].second;}return ans;}
};
复杂度分析:
- 时间复杂度:排序复杂度为 O ( n log n ) O(n\log n) O(nlogn) ;双指针构造答案的复杂度为 O ( n ) O(n) O(n) 。整体复杂度为 O ( n log n ) O(n\log{n}) O(nlogn)
- 空间复杂度: O ( n ) O(n) O(n)
相关文章:

LeetCode 436. Find Right Interval【排序,二分;双指针,莫队】中等
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

正则表达式 —— Sed
Sed Sed 类似于vim就是一个文本编辑器,按行来进行编辑和排序 Sed的原理:读取,执行,显示 读取:读取文本内容之后,读取到的内容存放到临时的缓冲区—模式空间 执行:在模式空间,根据…...

TypeScript中数组,元组 和 枚举类型
数组 方式一 let arr: number[] [1, 2, 3, 4]方式二,使用泛型定义 let arr: Array<number> [1, 2, 3, 4]方式三,使用any let arr: any[] [12, string, true] console.log(arr[1]) // string元组 可以定义不同类型定义类型顺序需保持一直 …...

MyBatis-Plus-Join 多表查询的扩展
文章目录 网站使用方法安装使用Lambda形式用法(MPJLambdaWrapper)简单的连表查询一对多查询 网站 官方网站:https://mybatisplusjoin.com/Github地址:https://github.com/yulichang/mybatis-plus-joinGitee地址:https…...

认清现实重新理解游戏的本质
认清现实重新理解游戏的本质 OVERVIEW 认清现实重新理解游戏的本质现实两条小路的启发四个动机1.当前的学习任务或工作任务太艰巨2.完美主义3.对未来太过于自信/无知4.大脑小看未来的收益 四个方法1.让未来的收益足够巨大2.让未来的收益感觉就在眼前3.玩游戏有恶劣的结果4.玩游…...
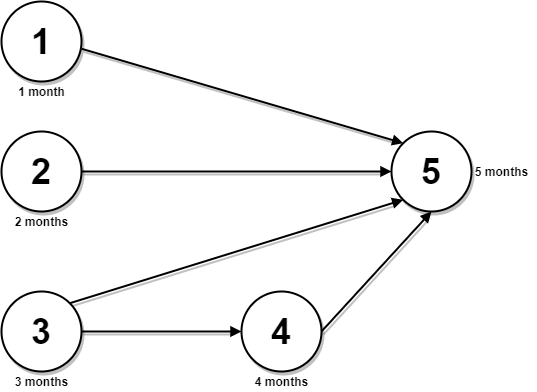
LeetCode 2050. Parallel Courses III【记忆化搜索,动态规划,拓扑排序】困难
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...
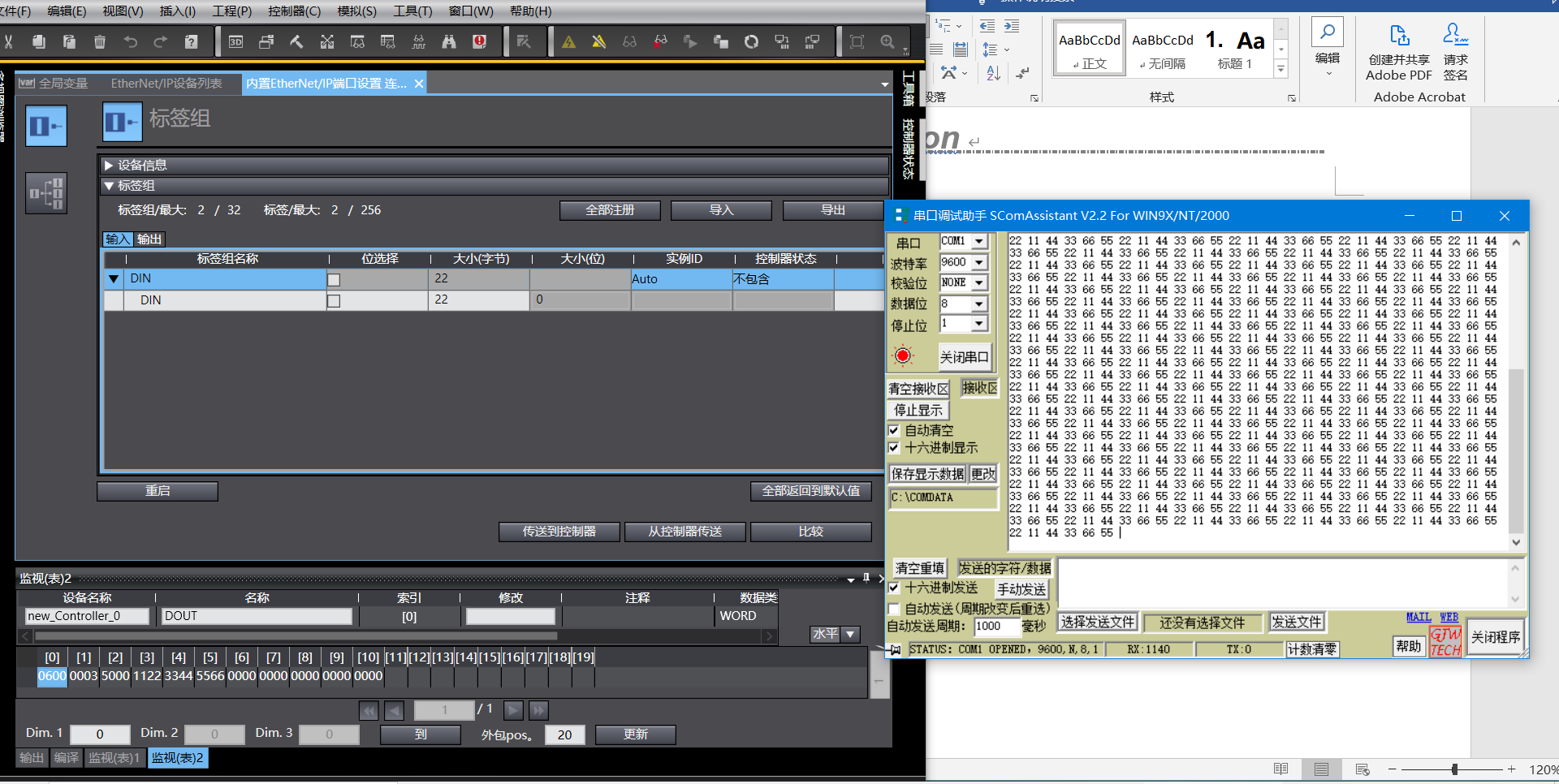
ETHERNET/IP转RS485/RS232网关什么是EtherNet/IP?
网络数据传输遇到的协议不同、数据互通麻烦等问题,一直困扰着大家。然而,现在有一种神器——捷米JM-EIP-RS485/232,它将ETHERNET/IP网络和RS485/RS232总线连接在一起,让数据传输更加便捷高效。 那么,它是如何实现这一功…...

使用node内置test runner,和 Jest say 拜拜
参考 https://nodejs.org/dist/latest-v20.x/docs/api/test.html#test-runner 在之前,我们写单元测试,必须安装第三方依赖包,而从node 20.0.0 版本之后,可以告别繁琐的第三方依赖包啦,可直接使用node的内置test runner…...

《面试1v1》Kafka的架构设计是什么样子
🍅 作者简介:王哥,CSDN2022博客总榜Top100🏆、博客专家💪 🍅 技术交流:定期更新Java硬核干货,不定期送书活动 🍅 王哥多年工作总结:Java学习路线总结…...

比较常见CPU的区别:Intel、ARM、AMD
一、开发公司不同 1、Intel:是英特尔公司开发的中央处理器,有移动、台式、服务器三个系列。 2、ARM:是英国Acorn有限公司设计的低功耗成本的第一款RISC微处理器。 3、AMD:由AMD公司生产的处理器。 二、技术不同 1、Intel&…...
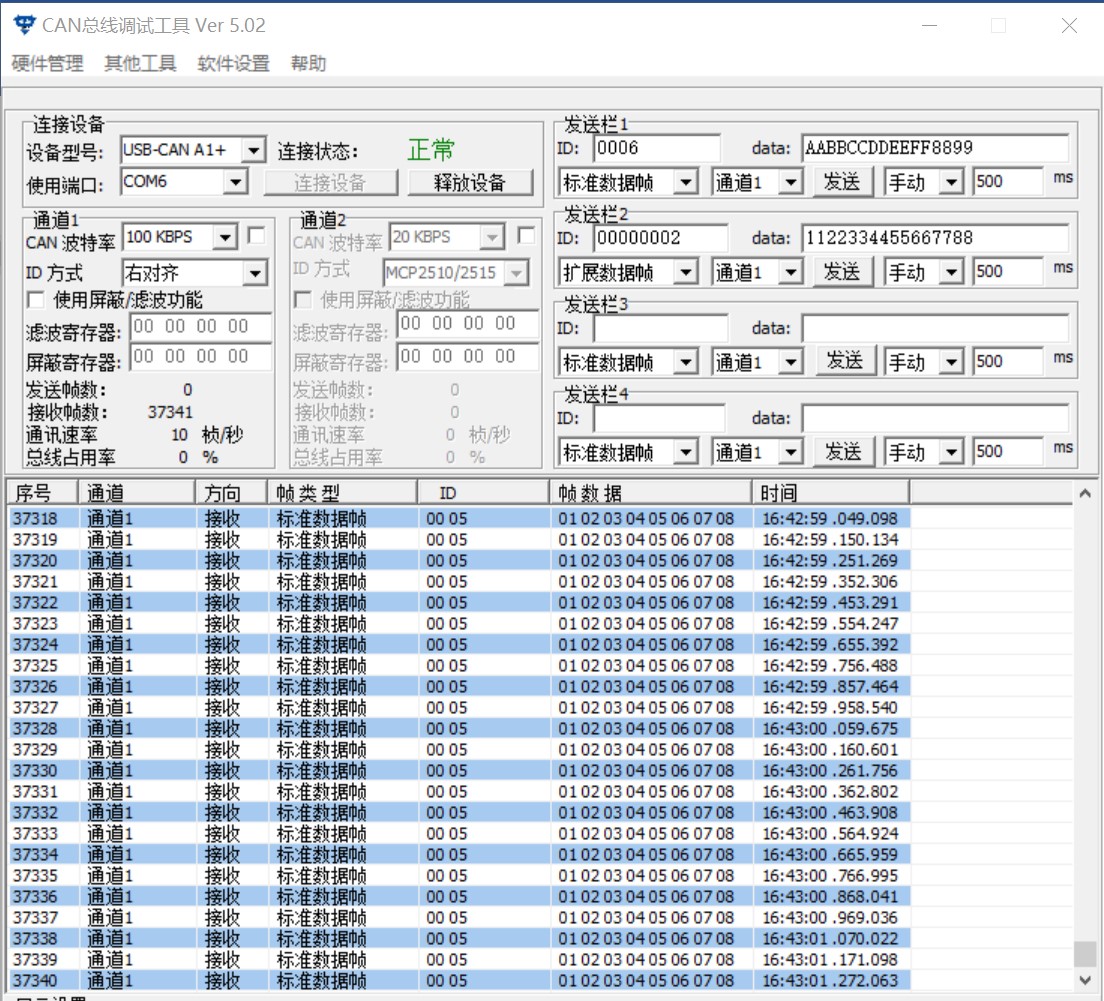
CAN转EtherNet/IP网关can协议是什么意思
你是否曾经遇到过不同的总线协议难以互相通信的问题?远创智控的YC-EIP-CAN网关为你解决了这个烦恼! 远创智控YC-EIP-CAN通讯网关是一款自主研发的设备,它能够将各种CAN总线和ETHERNET/IP网络连接起来,解决不同总线协议之间的通信…...
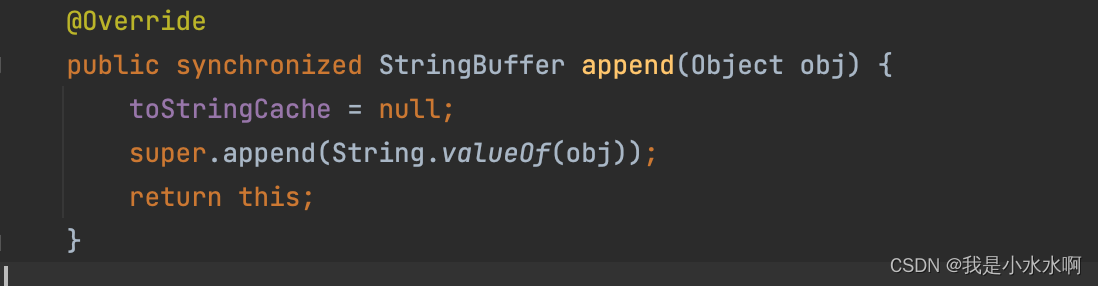
java可变字符序列:StringBuffer、StringBuilder
文章目录 StringBuffer与StringBuilder的理解StringBuilder、StringBuffer的API StringBuffer与StringBuilder的理解 因为String对象是不可变对象,虽然可以共享常量对象,但是对于频繁字符串的修改和拼接操作,效率极低,空间消耗也…...
Mac/win开发快捷键、vs插件、库源码、开发中的专业名词
目录 触控板手势(2/3指) 鼠标右键 快捷键 鼠标选择后shift⬅️→改变选择 mac command⬅️:删除←边的全部内容 commadtab显示下栏 commandshiftz向后撤回 commandc/v复制粘贴 command ⬅️→回到行首/末 commandshift3/4截图 飞…...

linux 系统编程
C标准函数与系统函数的区别 什么是系统调用 由操作系统实现并提供给外部应用程序的编程接口。(Application Programming Interface,API)。是应用程序同系统之间数据交互的桥梁。 一个helloworld如何打印到屏幕。 每一个FILE文件流(标准C库函数ÿ…...

Python策略模式介绍、使用方法
一、Python策略模式介绍 Python策略模式(Strategy Pattern)是一种软件设计模式,用于通过将算法封装为独立的对象,而使得它们可以在运行时动态地相互替换。该模式使得算法的变化独立于使用它们的客户端,从而达到代码的…...
城市气象数据可视化:洞察气候变化,构建智慧城市
随着城市化进程的加速,城市气象数据的采集和分析变得越来越重要。气象数据不仅影响着人们的生活和出行,还与城市的发展和规划息息相关。在数字化时代,如何将城市中各个气象数据进行可视化,让复杂的数据变得简单易懂,成…...

Rust-IO
use std::io::Write; fn main() {/*std::io::stdin() 返回标准输入流stdin的句柄。read_line() stdin的句柄的一个方法,从标准输入流中读取一行数据返回一个Result枚举。会自动删除行尾的换行符\n。unwrap() 是一个帮助的方法,简化恢复错误的处理。返回R…...

cp -r 源目录 目标目录
在Linux中,要复制目录可以使用cp命令。cp命令用于复制文件和目录。要复制整个目录及其内容,可以使用 -r 或 --recursive 参数来递归地复制目录。以下是示例命令:bash cp -r 源目录 目标目录其中: 源目录是要复制的目录的路径。目…...
redis之Bitmap
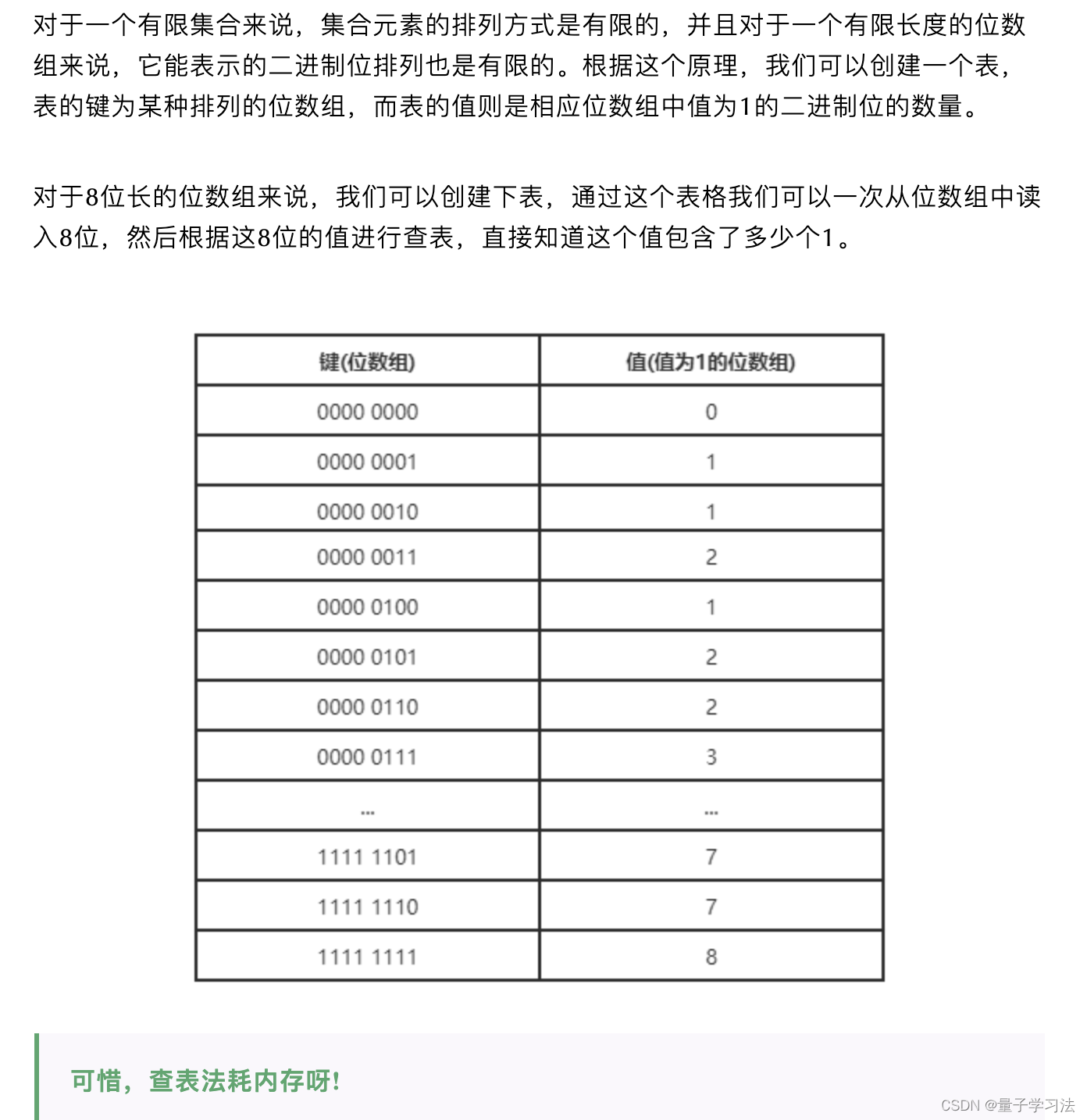
位图数据结构其实并不是一个全新的玩意,我们可以简单的认为就是个数组,只是里面的内容只能为0或1而已(二进制位数组)。 GETBIT用于返回位数组在偏移量上的二进制位的值。值得我们注意的是,GETBIT的时间复杂度是O(1)。 GETBIT命令的执行过程如…...
建设数据中台到底有啥用?
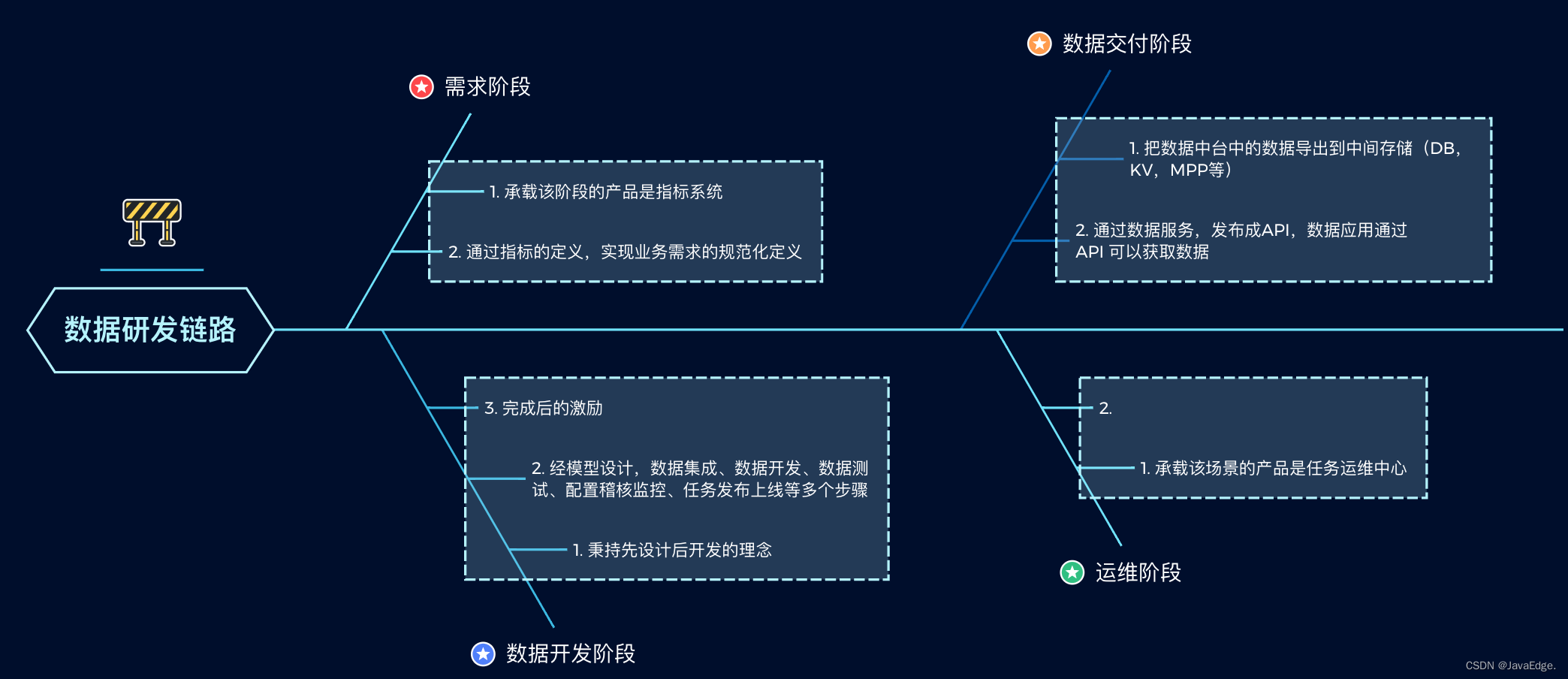
最近专注在数据和人工智能领域,从数据仓库、商业智能、主数据管理到大数据平台的建设,经过很多项目的沉淀和总结,最后我和团队一起总结了精益数据创新的体系。一直战斗在企业信息化一线。 企业为什么要建设数据中台,数据中台对于…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...
