最优化方法
一. 图论
1.最小生成树
图的生成树是它的一颗含有其所有顶点的无环连通子图,一 幅加权图的最小生成树(MST)是它的一颗权值(树中的所有边的权值之和) 最小的生成树
• 适用场景:道路规划、通讯网络规划、管道铺设、电线布设等
题目数据
kruskal算法
稀疏图,按边大小排序
#include<bits/stdc++.h>
using namespace std;
const int maxn=5e3+3,maxm=2e5+5;int n,m;
struct node{int fr,to,val;inline bool operator<(node b)const {return val<b.val;}
}e[maxm<<1];
int k,fa[maxn];
inline void add(int x,int y,int z){e[++k]=(node){x,y,z};}inline int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);
}
int main()
{scanf("%d %d",&n,&m);int x,y,z;for(int i=1;i<=m;i++) {scanf("%d %d %d",&x,&y,&z);add(x,y,z);add(x,y,z);//无向图 }sort(e+1,e+k+1); //边排序for(int i=1;i<=n;i++)fa[i]=i;//并查集初始化int cnt=0,ans=0;for(int i=1;i<=k;i++){int x=find(e[i].fr),y=find(e[i].to);if(x!=y){fa[x]=y;//连边ans+=e[i].val;++cnt;if(cnt==n-1)break;}}if(cnt==n-1)printf("%d",ans);else puts("orz");//图不连通return 0;
}
prim
稠密图
#include<bits/stdc++.h>
#define re return
#define inc(i,l,r) for(int i=l;i<=r;++i)
using namespace std;const int maxn=5e3+3,maxm=2e5+5;
int inf=5e8;
int n,m,d[maxn][maxn],dis[maxn],vis[maxn];
int main()
{// freopen("a.in","r",stdin);scanf("%d %d",&n,&m);int x,y,z;inc(i,1,n)inc(j,1,n)d[i][j]=inf;inc(i,1,m){scanf("%d %d %d",&x,&y,&z);d[x][y]=d[y][x]=min(d[x][y],z);}vis[1]=1;//将1号点加入图中 inc(i,2,n)dis[i]=d[1][i];//dis初始化为1到各个点之间的最短距离 int ans=0,cnt=n-1;while(cnt--)//需要进行n-1次循环 {int now,minn=inf;inc(i,1,n)if(!vis[i]&&dis[i]<minn)minn=dis[i],now=i;//找当前最短距离点 nowif(minn==inf){printf("orz");re 0;} vis[now]=1;ans+=dis[now];inc(i,1,n)dis[i]=min(dis[i],d[now][i]);}printf("%d",ans);re 0;
}
2.网络流
通常可以把这些边想象成道路,流量就是这条道 路的车流量,容量就是道路可承受的最大的车流量 • 适用场景:企业生产运输问题、交通拥堵优化问题等
最大流
题目数据
#include<bits/stdc++.h>
#define re return
#define inc(i,l,r) for(int i=l;i<=r;++i)
using namespace std;
template<typename T>inline void rd(T&x)
{char c;bool f=0;while((c=getchar())<'0'||c>'9')if(c=='-')f=1;x=c^48;while((c=getchar())>='0'&&c<='9')x=x*10+(c^48);if(f)x=-x;
}
const int maxn=1e4+4,maxm=1e5+5;
int n,m,hd[maxn],s,t;
struct node{int to,nt,w;
}e[maxm<<1];
int k=1;
inline void add(int x,int y,int z)
{e[++k]=(node){y,hd[x],z};hd[x]=k;e[++k]=(node){x,hd[y],0};hd[y]=k;
}int deep[maxn],cur[maxn];
inline bool bfs()
{inc(i,1,n)deep[i]=0;deep[s]=1;queue<int>q;q.push(s);while(!q.empty()){int x=q.front();q.pop();for(int i=hd[x];i;i=e[i].nt){int v=e[i].to;if(!deep[v]&&e[i].w){deep[v]=deep[x]+1;if(v==t)re 1;q.push(v);}}}re 0;
}inline int dfs(int x,int flow)
{if(x==t)re flow;int delta=flow;for(int &i=cur[x];i;i=e[i].nt){int v=e[i].to;if(deep[v]==deep[x]+1&&e[i].w){int d=dfs(v,min(e[i].w,delta));e[i].w-=d;e[i^1].w+=d;delta-=d;if(!delta)re flow;}}re flow-delta;
}
int main()
{rd(n),rd(m),rd(s),rd(t);int x,y,w;inc(i,1,m){rd(x),rd(y),rd(w);add(x,y,w);}int ans=0;while(bfs()){inc(i,1,n)cur[i]=hd[i];ans+=dfs(s,2147483647);}printf("%d",ans);re 0;
}
最小费用最大流
最大流量的基础上要求最小的费用,有边权值
题目数据
#include<bits/stdc++.h>
#define re return
#define inc(i,l,r) for(int i=l;i<=r;++i)
using namespace std;
template<typename T>inline void rd(T&x)
{char c;bool f=0;while((c=getchar())<'0'||c>'9')if(c=='-')f=1;x=c^48;while((c=getchar())>='0'&&c<='9')x=x*10+(c^48);if(f)x=-x;
}
const int maxn=5e3+3;int k=1,n,m,s,t;
int dis[maxn],ord[maxn],hd[maxn],flow[maxn],vis[maxn];
int smoney,sflow;struct node{int flow,to,nt,cost;
}e[100005];
inline void add(int u,int v,int w,int f)
{e[++k].to=v;e[k].nt=hd[u];e[k].flow=w;e[k].cost=f;hd[u]=k;
}inline bool spfa()
{queue<int>q;memset(dis,0x3f3f3f3f,sizeof dis);memset(vis,0,sizeof vis);q.push(s);dis[s]=0;flow[s]=0x3f3f3f3f;while(!q.empty()){int x=q.front();q.pop();vis[x]=0;for(int i=hd[x];i;i=e[i].nt){int v=e[i].to,w=e[i].flow,f=e[i].cost;if(w&&dis[v]>dis[x]+f){if(!vis[v]){vis[v]=1;q.push(v);}flow[v]=min(flow[x],w);dis[v]=dis[x]+f;ord[v]=i;}}}re dis[t]!=0x3f3f3f3f;
}inline void vivi()
{int x=t;while(x!=s){int i=ord[x];e[i].flow-=flow[t];e[i^1].flow+=flow[t];x=e[i^1].to;}sflow+=flow[t];smoney+=flow[t]*dis[t];
}
int main()
{
// freopen("a.in","r",stdin);rd(n),rd(m),rd(s),rd(t);int u,v,w,f;inc(i,1,m){rd(u),rd(v),rd(w),rd(f);add(u,v,w,f);add(v,u,0,-f);}while(spfa())vivi();printf("%d %d",sflow,smoney);re 0;
}
3.最短路
主要包括Dijkstra算法和Floyd算法两种,用于求解 两点间的最短距离 • 适用场景:路径规划问题,如修建道路、设定救援路线等
题目数据
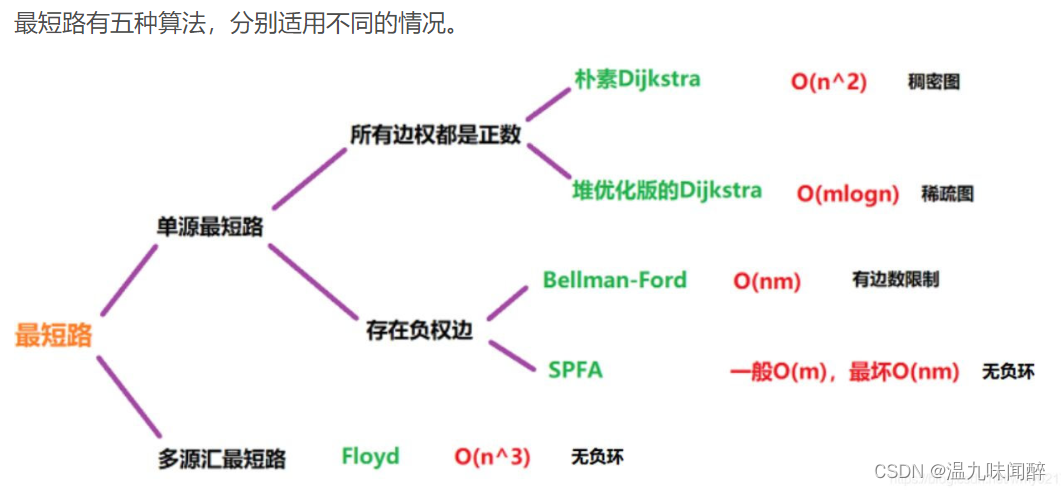
spfa
单源最短路
容易被卡
#include<bits/stdc++.h>
#define re return
#define inc(i,l,r) for(int i=l;i<=r;++i)
using namespace std;
template<typename T>inline void rd(T&x)
{char c;bool f=0;while((c=getchar())<'0'||c>'9')if(c=='-')f=1;x=c^48;while((c=getchar())>='0'&&c<='9')x=x*10+(c^48);if(f)x=-x;
}const int maxn=1e4+5,maxm=5e5+5;
int n,m,hd[maxn];
struct node{int to,nt,val;
}e[maxm<<1];
int k,s;
inline void add(int x,int y,int z){e[++k]=(node){y,hd[x],z};hd[x]=k;
}#define ll long long
ll inf=2147483647,dis[maxn],vis[maxn];
inline void spfa()
{inc(i,1,n)dis[i]=inf;dis[s]=0;queue<int>q;q.push(s);while(!q.empty()){int x=q.front();q.pop();vis[x]=0;for(int i=hd[x];i;i=e[i].nt){int v=e[i].to;if(dis[v]>dis[x]+e[i].val){dis[v]=dis[x]+e[i].val;if(!vis[v]){vis[v]=1;q.push(v); }}}}
}int main()
{// freopen("a.in","r",stdin);rd(n),rd(m),rd(s);int x,y,z;inc(i,1,m){rd(x),rd(y),rd(z);add(x,y,z);}spfa();inc(i,1,n)printf("%lld ",dis[i]);re 0;
}
dijsktra
单源最短路
无负边
#include<bits/stdc++.h>
#define re return
#define inc(i,l,r) for(int i=l;i<=r;++i)
using namespace std;
template<typename T>inline void rd(T&x)
{char c;bool f=0;while((c=getchar())<'0'||c>'9')if(c=='-')f=1;x=c^48;while((c=getchar())>='0'&&c<='9')x=x*10+(c^48);if(f)x=-x;
}const int maxn=1e4+5,maxm=5e5+5;
int n,m,hd[maxn];
struct node{int to,nt,val;
}e[maxm<<1];
int k,s;
inline void add(int x,int y,int z){e[++k]=(node){y,hd[x],z};hd[x]=k;
}#define ll long long
ll inf=2147483647,dis[maxn];
struct KKK{
int x,val;
inline bool operator<(KKK u)const
{re val>u.val;
}
};
inline void dij()
{inc(i,1,n)dis[i]=inf;dis[s]=0;priority_queue<KKK>q;q.push((KKK){s,0});while(!q.empty()){KKK u=q.top();q.pop();int x=u.x;if(dis[x]!=u.val)continue;for(int i=hd[x];i;i=e[i].nt){int v=e[i].to;if(dis[v]>dis[x]+e[i].val){dis[v]=dis[x]+e[i].val;q.push((KKK){v,dis[v]});}}}
}int main()
{//freopen("a.in","r",stdin);rd(n),rd(m),rd(s);int x,y,z;inc(i,1,m){rd(x),rd(y),rd(z);add(x,y,z);}dij();inc(i,1,n)printf("%lld ",dis[i]);re 0;
}
floyd
O(n^3)
多源最短路
#include<bits/stdc++.h>
using namespace std;
#define inf 1234567890
#define maxn 10005
inline int read()
{int x=0,k=1; char c=getchar();while(c<'0'||c>'9'){if(c=='-')k=-1;c=getchar();}while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+(c^48),c=getchar();return x*k;
}//快读
int a[maxn][maxn],n,m,s;
inline void floyd()
{for(int k=1;k<=n;k++)//这里要先枚举k(可以理解为中转点){for(int i=1;i<=n;i++){if(i==k||a[i][k]==inf){continue;}for(int j=1;j<=n;j++){a[i][j]=min(a[i][j],a[i][k]+a[k][j]);//松弛操作,即更新每两个点之间的距离//松弛操作有三角形的三边关系推出//即两边之和大于第三边}}}
}
int main()
{n=read(),m=read(),s=read();for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){a[i][j]=inf;}}//初始化,相当于memset(a,inf,sizeof(a))for(int i=1,u,v,w;i<=m;i++){u=read(),v=read(),w=read();a[u][v]=min(a[u][v],w);//取min可以对付重边}floyd();a[s][s]=0;for(int i=1;i<=n;i++){printf("%d ",a[s][i]);}return 0;
}
二、动态规划
dp数学建模的应用不多,感觉主要还是各种环境下的一个背包(多维dp),对于状压,数位都不怎么涉及
总的思想来说偏向背包较为单一,找递归方程时的问题主要在于结合其他信息,可能涉及到概率(马尔科夫链),图(偏向树形dp之类的)
- 背包
采药
一维
#include<bits/stdc++.h>
using namespace std;
int a[100001];
int o;
int main()
{int t,m;cin>>t>>m;
int w[m+1],v[m+1];
for(int i=1;i<=m;i++)
cin>>w[i]>>v[i];for(int j=1;j<=t;j++) for(int k=1;k<=m;k++){a[j]=o;if(j>=w[k]){a[j]=max(a[j],a[j-w[k]]+v[k]); o=max(o,a[j]);}}cout<<a[t];return 0;
}
二维
#include<bits/stdc++.h>
using namespace std;
int a[101][1001];
int main()
{
int n,m;
cin>>n>>m;
int w[m+1];
int v[m+1];
for(int i=1;i<=m;i++)
cin>>w[i]>>v[i];for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
{ a[i][j]=a[i-1][j];
if(j>=w[i])a[i][j]=max(a[i-1][j-w[i]]+v[i],a[i][j]); }
cout<<a[m][n];
return 0;
}
2.树形dp
在连通图上dp
没有上司的舞会
#include<bits/stdc++.h>
using namespace std;
int f[6005][3],head[6005],cc[6005],in[6005];
int n,a,b,c;void dfs(int x)
{ for(int i=head[x];i!=0;i=cc[i]){ dfs(i);f[x][1]=f[x][1]+f[i][0];f[x][0]+=max(f[i][0],f[i][1]);}
}int main()
{ scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&f[i][1]);for(int i=1;i<n;i++)
{scanf("%d%d",&a,&b);
cc[a]=head[b];
head[b]=a;in[a]=1;}for(int i=1;i<=n;i++)
if(in[i]==0){c=i;break;}
dfs(c);
printf("%d",max(f[c][1],f[c][0]));return 0;
}
三、启发式算法
模拟退火
模拟退火算法(Simulate Anneal,SA)是一种通用概率演算法,用来在一个大的搜寻空间内找寻命题的最优解。
https://www.cnblogs.com/flashhu/p/8884132.html
#include<bits/stdc++.h>
#define re return
#define st static
#define mem(a,b) memset((a),(b),sizeof(a))
#define inc(i,l,r) for(register int i=l;i<=r;++i)
#define dec(i,l,r) for(register int i=l;i>=r;--i)using namespace std;
int n,x[1005],y[1005],w[1005];
double EPS=10e-15,D=0.975;double calc(double x0,double y0)
{double res=0;inc(i,1,n)res+=sqrt((x[i]-x0)*(x[i]-x0)+(y[i]-y0)*(y[i]-y0))*w[i];re res;
}int main()
{
// freopen("in.txt","r",stdin);double x1=0,y1=0,x0,y0,bx,by,res,ans,best,time=2;scanf("%d",&n);inc(i,1,n){scanf("%d%d%d",&x[i],&y[i],&w[i]);bx+=x[i];by+=y[i];}best=calc(bx/=n,by/=n);//用平均值作为最初解srand(20130317);while(time--){x1=bx,y1=by,ans=best;for(double T=100000;T>EPS;T*=D){x0=x1+T*(2*rand()-RAND_MAX);y0=y1+T*(2*rand()-RAND_MAX);res=calc(x0,y0);if(res<best){best=res;bx=x0;by=y0;}if(res<ans||exp((ans-res)/T)>(double)(rand())/RAND_MAX){ans=res;x1=x0;y1=y0;}}}printf("%.3lf %.3lf",bx,by);re 0;
}
相关文章:

最优化方法
一. 图论 1.最小生成树 图的生成树是它的一颗含有其所有顶点的无环连通子图,一 幅加权图的最小生成树(MST)是它的一颗权值(树中的所有边的权值之和) 最小的生成树 • 适用场景:道路规划、通讯网络规划、管道铺设、电线布设等 题目数据 kruskal算法 稀疏图&#x…...
)
Mongodb 多文档聚合操作处理方法二(Map-reduce 函数)
聚合 聚合操作处理多个文档并返回计算结果。您可以使用聚合操作来: 将多个文档中的值分组在一起。 对分组数据执行操作以返回单个结果。 分析数据随时间的变化。 要执行聚合操作,您可以使用: 聚合管道 单一目的聚合方法 Map-reduce 函…...

ant design vue j-modal 修改高度
问题描述 今天在项目中遇到关于j-modal组件修改弹窗大小问题,我尝试使用直接使用:height"300",没用效果,弹窗大小依然和没改之前一样,后来找到了这种方式可以去修改j-modal弹窗大小,下面来看下代码实现&…...

spring学习笔记七
一、自动装配 1.1、BookDao接口和实现类 public interface BookDao {void save(); } public class BookDaoImpl implements BookDao {public void save(){System.out.println("book dao save......");} } 1.2、BookService接口和实现类 public interface BookSer…...

hw技战法整理参考
目录 IP溯源反制 账户安全策略及预警 蜜罐部署联动方案...

uniapp 全局数据(globalData)的设置,获取,更改
globalData,这是一种简单的全局变量机制。这套机制在uni-app里也可以使用,并且全端通用 因为uniapp基本上都是将页面,或者页面中相同的部分,进行组件化,所以会存在父,子,(子…...
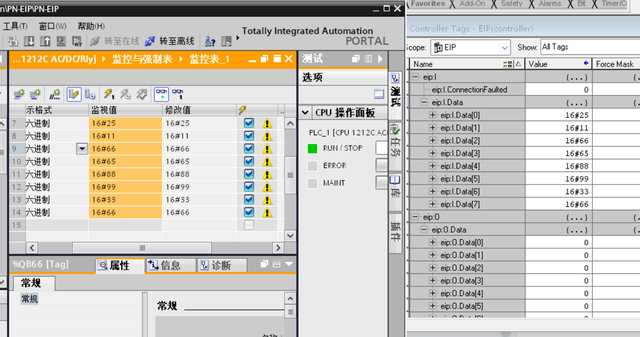
Profinet转EtherNet/IP网关连接AB PLC的应用案例
西门子S7-1500 PLC(profinet)与AB PLC以太网通讯(EtherNet/IP)。本文主要介绍捷米特JM-EIP-PN的Profinet转EtherNet/IP网关,连接西门子S7-1500 PLC与AB PLC 通讯的配置过程,供大家参考。 1, 新建工程&…...

Python组合模式介绍、使用方法
一、Python组合模式介绍 概念: 组合模式(Composite Pattern)是一种结构型设计模式,它通过将对象组合成树状结构来表示“整体/部分”层次结构,让客户端可以以相同的方式处理单个对象和组合对象。 功能: 统一对待组合对象和叶子对…...
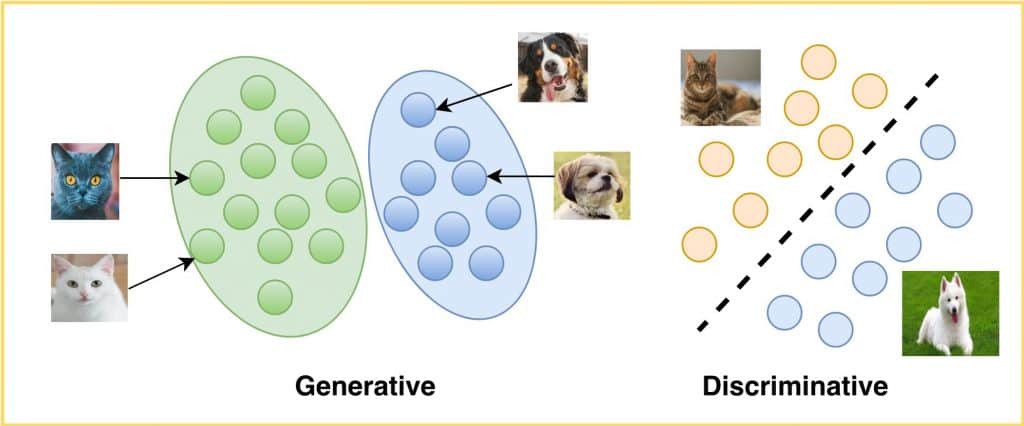
生成模型和判别模型工作原理介绍
您解决的大多数机器学习和深度学习问题都是从生成模型和判别模型中概念化的。在机器学习中,人们可以清楚地区分两种建模类型: 将图像分类为狗或猫属于判别性建模生成逼真的狗或猫图像是一个生成建模问题神经网络被采用得越多,生成域和判别域就增长得越多。要理解基于这些模型…...

shardingsphere读写分离配置
注: 如果是升级之前的单库单表,要将之前的 数据库接池 druid-spring-boot-starter 注释掉,换成 druid,否则无法连接数据库。 原因: 因为数据连接池的starter(比如druid)可能会先加载并且其创…...
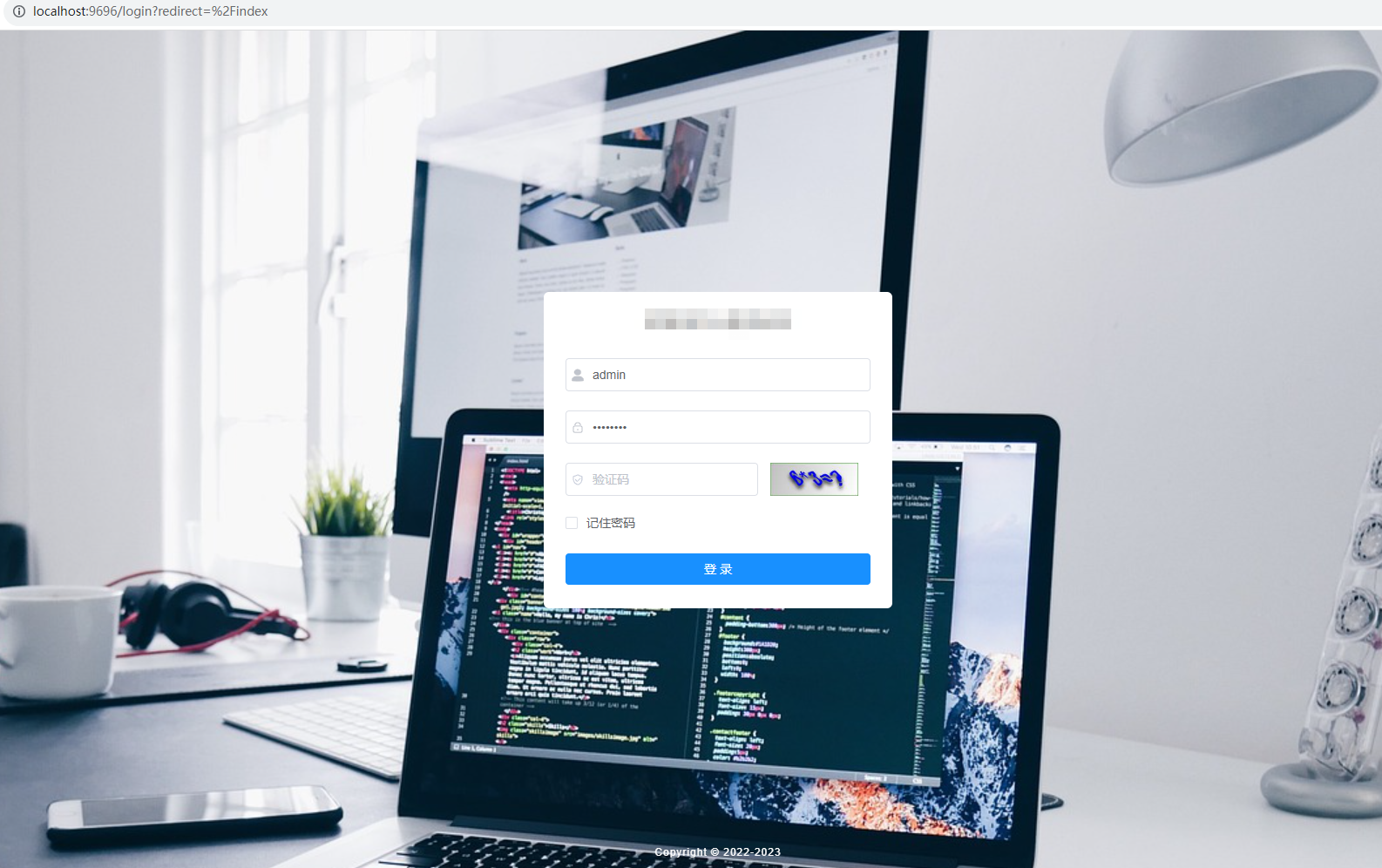
登录报错 “msg“:“Request method ‘GET‘ not supported“,“code“:500
1. 登录失败 2. 排查原因, 把 PostMapping请求注释掉, 或改成GetMapping请求就不会报错 3. 找到SecurityConfig.java , 新增 .antMatchers("/**/**").permitAll() //匹配允许所有路径 4. 登录成功...

Python 日期和时间
Python 日期和时间 Python 程序能用很多方式处理日期和时间,转换日期格式是一个常见的功能。 Python 提供了一个 time 和 calendar 模块可以用于格式化日期和时间。 时间间隔是以秒为单位的浮点小数。 每个时间戳都以自从1970年1月1日午夜(历元&…...
pytorch的发展历史,与其他框架的联系
我一直是这样以为的:pytorch的底层实现是c(这一点没有问题,见下边的pytorch结构图),然后这个部分顺理成章的被命名为torch,并提供c接口,我们在python中常用的是带有python接口的,所以被称为pytorch。昨天无意中看到Torch是由lua语言写的&…...

Kibana-elastic--Elastic Stack--ELK Stack
Kibana 是什么? | Elastic 将数据转变为结果、响应和解决方案 使用 Kibana 针对大规模数据快速运行数据分析,以实现可观测性、安全和搜索。对来自任何来源的任何数据进行全面透彻的分析,从威胁情报到搜索分析,从日志到应用程序监测…...

Docker复杂命令便捷操作
启动所有状态为Created的容器 要启动所有状态为"created"的Docker容器,可以使用以下命令: docker container start $(docker container ls -aq --filter "statuscreated")上述命令执行了以下步骤: docker container l…...
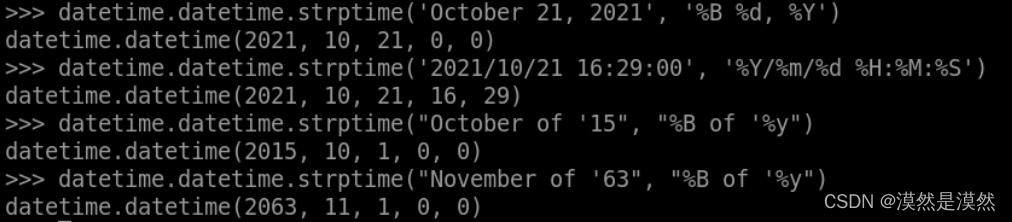
Python中的datetime模块
time模块用于取得UNIX纪元时间戳,并加以处理。但是,如果以方便的格式显示日期,或对日期进行算数运算,就应该使用datetime模块。 目录 1. datetime数据类型 1) datetime.datetime.now()表示特定时刻 2)da…...
Flutter - 微信朋友圈、十字滑动效果(微博/抖音个人中心效果)
demo 地址: https://github.com/iotjin/jh_flutter_demo 代码不定时更新,请前往github查看最新代码 前言 一般APP都有类似微博/抖音个人中心的效果,支持上下拉刷新,并且顶部有个图片可以下拉放大,图片底部是几个tab,可…...

MySQL检索数据和排序数据
目录 一、select语句 1.检索单个列(SELECT 列名 FROM 表名;) 2.检索多个列(SELECT 列名1,列名2,列名3 FROM 表名;) 3.检索所有的列(SELECT * FROM 表名;) 4.检索不同的行&#x…...
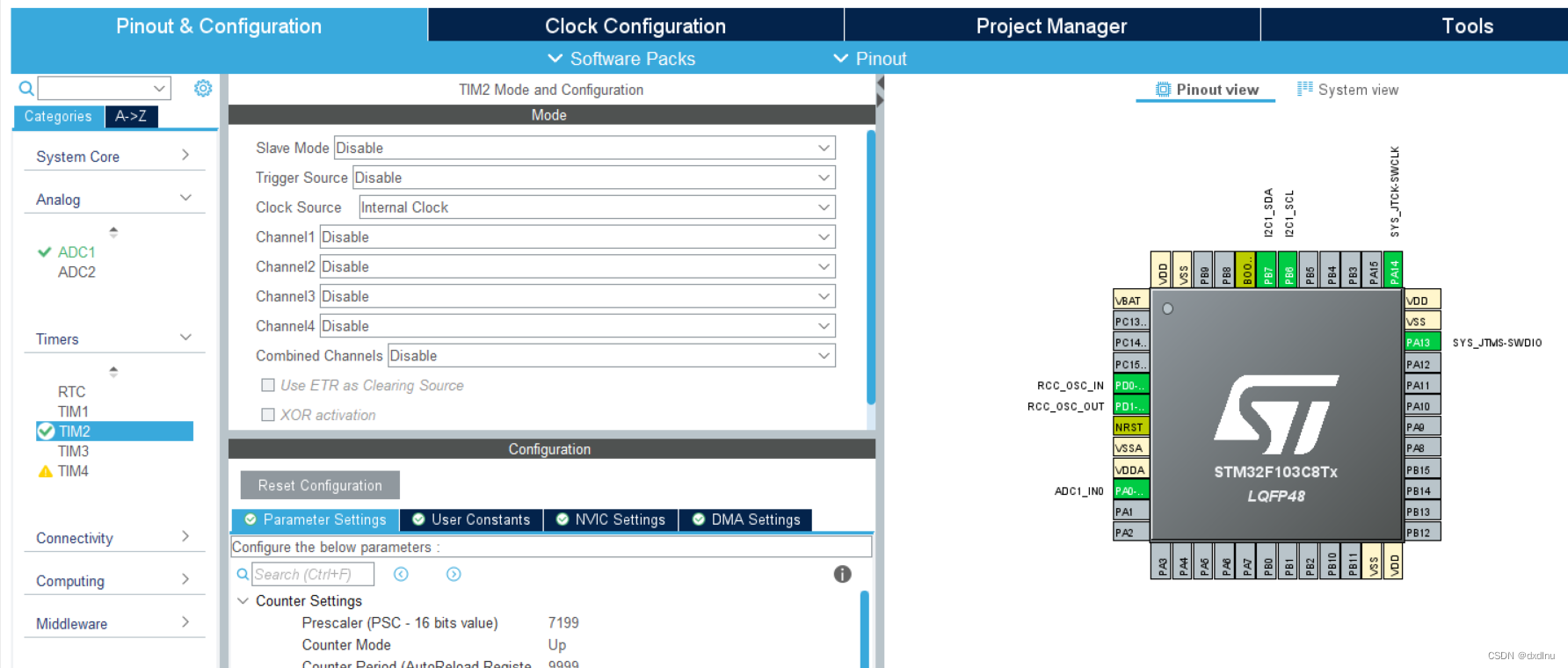
通过STM32内部ADC将烟雾传感器发送的信号值显示在OLED上
一.CubeMX配置 首先我们在CubeMX配置ADC1, 设置一个定时器TIM2定时1s采样一次以及刷新一次OLED, 打开IIC用于驱动OLED显示屏。 二.程序 在Keil5中添加好oled的显示库,以及用来显示的函数、初始化函数、清屏函数等。在主程序中初始化oled,并将其清屏。…...

ZEPHYR 快速开发指南
简介 国内小伙伴在学习zephyr的时候,有以下几个痛点: 学习门槛过高github访问不畅,下载起来比较费劲。 这篇文章将我自己踩的坑介绍一下,顺便给大家优化一些地方,避免掉所有的坑。 首先用virtualbox 来安装一个ubu…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

算法—栈系列
一:删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...
