医学图像重建—第一章笔记
序言
本书涵盖内容:
2D parallel beam imaging
2D fan beam imaging
3D parallel ray imaging
3D parallel plane imaging
3D cone beam imaging
算法包括:analytical method,iterative method
应用于:
X-ray CT
single photon emission CT(SPECT)
positron emission tomography(PET)
magnetic resonance imaging(MRI)
层析的基本原理
tomos:希腊语,意为截面,切片。
tomography:横截面成像的过程。
断层成像:得到物体内部的截面图像。
CT:computed tomography,计算机断层成像。
图像重建:由物体投影数据得到断层成像。
投影即射线和,线积分,radon变换。
下面举几个投影的例子:
1、二维 x-y 平面中的一个均匀圆盘,圆盘的圆心在坐标原点。圆盘投影值表示为:
p ( s ) = 2 ρ R 2 − s 2 , ∣ s ∣ < R p(s) = 2\rho \sqrt{R^2-s^2}, |s|<R p(s)=2ρR2−s2,∣s∣<R
p ( s ) = 0 , ∣ s ∣ ≥ R p(s) = 0, |s|\geq R p(s)=0,∣s∣≥R
由于圆盘是中心对称的几何体,因此对于所有角度来说,投影都一样: p ( s , θ ) = p ( s ) p(s,\theta)=p(s) p(s,θ)=p(s)
2、 y 轴上坐标为 ( 0 , r ) (0,r) (0,r)的点源投影:
p ( s , θ ) = 1 , s = r s i n θ p(s, \theta) = 1, s=rsin\theta p(s,θ)=1,s=rsinθ
p ( s , θ ) = 0 , s ≠ r s i n θ p(s, \theta) = 0, s\neq rsin\theta p(s,θ)=0,s=rsinθ
探测器旋转一圈,采集到的投影数据是一个正弦函数。
由此,人们将投影数据称为正弦图。
点源重建:解出点源的位置以及数值。
投影数据:沿着每条与探测器垂直的直线,对物体求线积分。
反投影:沿着每条与探测器垂直的直线,将投影数据均匀涂抹回去。
反投影导致边缘模糊不清,先在点源投影脉冲两边添加一对负值的翅膀(滤波)再进行反投影。(FBP,Filtered Backprojection)
点源重建只需要两个角度投影数据。
反投影的定义取决于投影是如何定义的。但反投影运算并不是投影运算的逆运算,反投影算子不是投影算子的逆算子。
一个2x2的矩阵: A = [ a i j ] 2 × 2 A=[a_{ij}]_{2\times 2} A=[aij]2×2,对其进行0度与90度的投影:
p 11 = a 11 + a 21 p_{11} = a_{11} + a_{21} p11=a11+a21
p 12 = a 12 + a 22 p_{12} = a_{12} + a_{22} p12=a12+a22
p 21 = a 11 + a 12 p_{21} = a_{11} + a_{12} p21=a11+a12
p 22 = a 21 + a 22 p_{22} = a_{21} + a_{22} p22=a21+a22
进行反投影:
B = [ p 11 + p 21 p 12 + p 21 p 11 + p 22 p 12 + p 22 ] B=\begin{bmatrix} p_{11} + p_{21} & p_{12} + p_{21}\\ p_{11} + p_{22} & p_{12} + p_{22} \end{bmatrix} B=[p11+p21p11+p22p12+p21p12+p22]
原矩阵,投影矩阵,反投影矩阵: A , P , B A,P,B A,P,B,三者存在以下关系:
P = C A P = CA P=CA
B = C T P B = C^TP B=CTP
B = C T C A B = C^T C A B=CTCA
反投影算子 C T C^T CT与投影算子 C C C的关系不是求逆而是共轭转置
f ( x , y ) f(x,y) f(x,y)为物体截面密度函数
投影函数(射线和,线积分,Radon变换)有下面下面几种表达方式:
p ( s , θ ) = ∫ ∫ f ( x , y ) δ ( x c o s θ + y s i n θ − s ) d x d y p(s,\theta)=\int \int f(x,y)\delta(xcos\theta + ysin\theta -s)dxdy p(s,θ)=∫∫f(x,y)δ(xcosθ+ysinθ−s)dxdy
p ( s , θ ) = ∫ ∫ f ( x , y ) δ ( x ⃗ ⋅ θ ⃗ − s ) d x d y p(s,\theta)=\int \int f(x,y)\delta(\vec{x}\cdot \vec{\theta} -s)dxdy p(s,θ)=∫∫f(x,y)δ(x⋅θ−s)dxdy
p ( s , θ ) = ∫ f ( s c o s θ − t s i n θ , s s i n θ + t c o s θ ) d t p(s,\theta)=\int f(scos\theta - tsin\theta, ssin\theta+tcos\theta)dt p(s,θ)=∫f(scosθ−tsinθ,ssinθ+tcosθ)dt
p ( s , θ ) = ∫ f ( θ ⃗ + t θ ′ ⃗ ) d t p(s,\theta)=\int f(\vec{\theta} + t\vec{\theta'})dt p(s,θ)=∫f(θ+tθ′)dt
p ( s , θ ) = ∫ f θ ( s , t ) d t p(s,\theta)=\int f_{\theta}(s,t)dt p(s,θ)=∫fθ(s,t)dt
以上表达式积分范围为 [ − ∞ , ∞ ] [-\infty, \infty] [−∞,∞]
θ ⃗ , θ ′ ⃗ \vec{\theta}, \vec{\theta'} θ,θ′为垂直与平行于平行束方向的单位向量。
θ \theta θ为探测器绕物体逆时针转,等价于物体绕旋转中心顺时针转。
反投影图像的几种表达方式:
b ( x , y ) = ∫ 0 π p ( s , θ ) ∣ s = x c o s θ + y s i n θ d θ b(x,y) = \int_0^\pi p(s,\theta)|_{s=xcos\theta + ysin\theta}d\theta b(x,y)=∫0πp(s,θ)∣s=xcosθ+ysinθdθ
b ( x , y ) = ∫ 0 π p ( s , θ ) ∣ s = x ⃗ ⋅ θ ⃗ d θ b(x,y) = \int_0^\pi p(s,\theta)|_{s=\vec{x} \cdot \vec{\theta}}d\theta b(x,y)=∫0πp(s,θ)∣s=x⋅θdθ
b ( x , y ) = ∫ 0 π p ( x ⃗ ⋅ θ ⃗ , θ ) d θ b(x,y) = \int_0^\pi p(\vec{x} \cdot \vec{\theta},\theta) d\theta b(x,y)=∫0πp(x⋅θ,θ)dθ
b ( x , y ) = 1 2 ∫ 0 2 π p ( s , θ ) ∣ s = x c o s θ + y s i n θ d θ b(x,y) = \frac{1}{2}\int_0^{2\pi} p(s,\theta)|_{s=xcos\theta + ysin\theta}d\theta b(x,y)=21∫02πp(s,θ)∣s=xcosθ+ysinθdθ
函数 f ( x ⃗ ) = δ ( x ⃗ − x ⃗ 0 ) = δ ( x − x 0 ) δ ( y − y 0 ) f(\vec{x}) = \delta(\vec{x} - \vec{x}_0) = \delta(x - x_0)\delta(y - y_0) f(x)=δ(x−x0)=δ(x−x0)δ(y−y0)的Radon变换:(逐步推导)
p ( s , θ ) = ∫ ∫ f ( x ⃗ ) δ ( x ⃗ ⋅ θ ⃗ − s ) d x d y p(s,\theta)=\int \int f(\vec{x})\delta(\vec{x}\cdot \vec{\theta} -s)dxdy p(s,θ)=∫∫f(x)δ(x⋅θ−s)dxdy
p ( s , θ ) = ∫ ∫ δ ( x − x 0 ) δ ( y − y 0 ) δ ( x c o s θ + y s i n θ − s ) d x d y p(s,\theta)=\int \int \delta(x - x_0)\delta(y - y_0) \delta(xcos\theta + ysin\theta -s)dxdy p(s,θ)=∫∫δ(x−x0)δ(y−y0)δ(xcosθ+ysinθ−s)dxdy
p ( s , θ ) = ∫ δ ( y − y 0 ) ∫ δ ( x − x 0 ) δ ( x c o s θ + y s i n θ − s ) d x d y p(s,\theta)=\int \delta(y - y_0) \int \delta(x - x_0) \delta(xcos\theta + ysin\theta -s)dxdy p(s,θ)=∫δ(y−y0)∫δ(x−x0)δ(xcosθ+ysinθ−s)dxdy
p ( s , θ ) = ∫ δ ( y − y 0 ) δ ( x 0 c o s θ + y s i n θ − s ) d y p(s,\theta)=\int \delta(y - y_0) \delta(x_0cos\theta + ysin\theta -s)dy p(s,θ)=∫δ(y−y0)δ(x0cosθ+ysinθ−s)dy
p ( s , θ ) = δ ( x 0 c o s θ + y 0 s i n θ − s ) p(s,\theta)=\delta(x_0cos\theta + y_0sin\theta -s) p(s,θ)=δ(x0cosθ+y0sinθ−s)
这里运用了 δ \delta δ函数的第一条性质。
补充
之前共轭转置和代数余子式转置都叫做adjoint
现在共轭转置叫adjugate,代数余子式转置叫classical adjoint
代数余子式转置: C ∗ = ∣ C ∣ C − 1 C^* = |C|C^{-1} C∗=∣C∣C−1
共轭转置: C ∗ = C H = c o n j ( C T ) C^* = C^H = conj(C^T) C∗=CH=conj(CT)
因此书上的这个伴随只得是共轭转置。
参考:[学习笔记]共轭转置矩阵与伴随矩阵都用A*表示合理吗? - 裴以鹏的文章 - 知乎. https://zhuanlan.zhihu.com/p/87330558.
狄拉克分布函数 δ ( x ) \delta(x) δ(x)可以通过高斯函数 G ( x , n ) G(x,n) G(x,n)来定义:
l i m n → ∞ ∫ − ∞ ∞ G ( x , n ) f ( x ) d x = ∫ − ∞ ∞ δ ( x ) f ( x ) d x = f ( 0 ) lim_{n\rightarrow \infty} \int_{-\infty}^{\infty} G(x,n)f(x)dx =\int_{-\infty}^{\infty} \delta(x) f(x)dx = f(0) limn→∞∫−∞∞G(x,n)f(x)dx=∫−∞∞δ(x)f(x)dx=f(0)
其中, f ( x ) f(x) f(x)为一个平滑函数,对于任意N有 l i m x → ∞ x N f ( x ) = 0 lim_{x\rightarrow \infty} x^N f(x) = 0 limx→∞xNf(x)=0, G ( x , n ) = ( n / π ) 1 / 2 e − n x 2 G(x,n) = (n/\pi)^{1/2} e^{-nx^2} G(x,n)=(n/π)1/2e−nx2
δ ( x ) \delta(x) δ(x)的性质:
∫ − ∞ ∞ δ ( x − a ) f ( x ) d x = ∫ − ∞ ∞ δ ( x ) f ( x + a ) d x = f ( a ) \int_{-\infty}^{\infty} \delta(x-a)f(x)dx = \int_{-\infty}^{\infty} \delta(x)f(x+a)dx = f(a) ∫−∞∞δ(x−a)f(x)dx=∫−∞∞δ(x)f(x+a)dx=f(a)
∫ − ∞ ∞ δ ( a x ) f ( x ) d x = f ( 0 ) / ∣ a ∣ \int_{-\infty}^{\infty} \delta(ax)f(x)dx = f(0)/|a| ∫−∞∞δ(ax)f(x)dx=f(0)/∣a∣
∫ − ∞ ∞ δ ( n ) ( x ) f ( x ) d x = ( − 1 ) n f ( n ) ( 0 ) \int_{-\infty}^{\infty} \delta^{(n)}(x)f(x)dx = (-1)^n f^{(n)}(0) ∫−∞∞δ(n)(x)f(x)dx=(−1)nf(n)(0)
δ ( g ( x ) ) f ( x ) = Σ n δ ( x − λ n ) / ∣ g ′ ( λ n ) ∣ \delta (g(x)) f(x) = \Sigma_n \delta(x-\lambda_n)/|g'(\lambda_n)| δ(g(x))f(x)=Σnδ(x−λn)/∣g′(λn)∣, λ n \lambda_n λn为 g g g的零点
二维狄拉克分布函数 δ ( x ⃗ ) = δ ( x ) δ ( y ) \delta (\vec{x}) = \delta(x)\delta(y) δ(x)=δ(x)δ(y)
三维狄拉克分布函数 δ ( x ⃗ ) = δ ( x ) δ ( y ) δ ( z ) \delta (\vec{x}) = \delta(x)\delta(y)\delta(z) δ(x)=δ(x)δ(y)δ(z)
相关文章:

医学图像重建—第一章笔记
序言 本书涵盖内容: 2D parallel beam imaging 2D fan beam imaging 3D parallel ray imaging 3D parallel plane imaging 3D cone beam imaging 算法包括:analytical method,iterative method 应用于: X-ray CT single photon…...

python-pytorch基础之神经网络分类
这里写目录标题 生成数据函数定义数据集定义loader加载数据定义神经网络模型测试输出是否为2个输入数据,输出结果 训练模型函数计算正确率 训练数据并保存模型测试模型准备数据加载模型预测对比结果 生成数据函数 import randomdef get_rectangle():widthrandom.ra…...
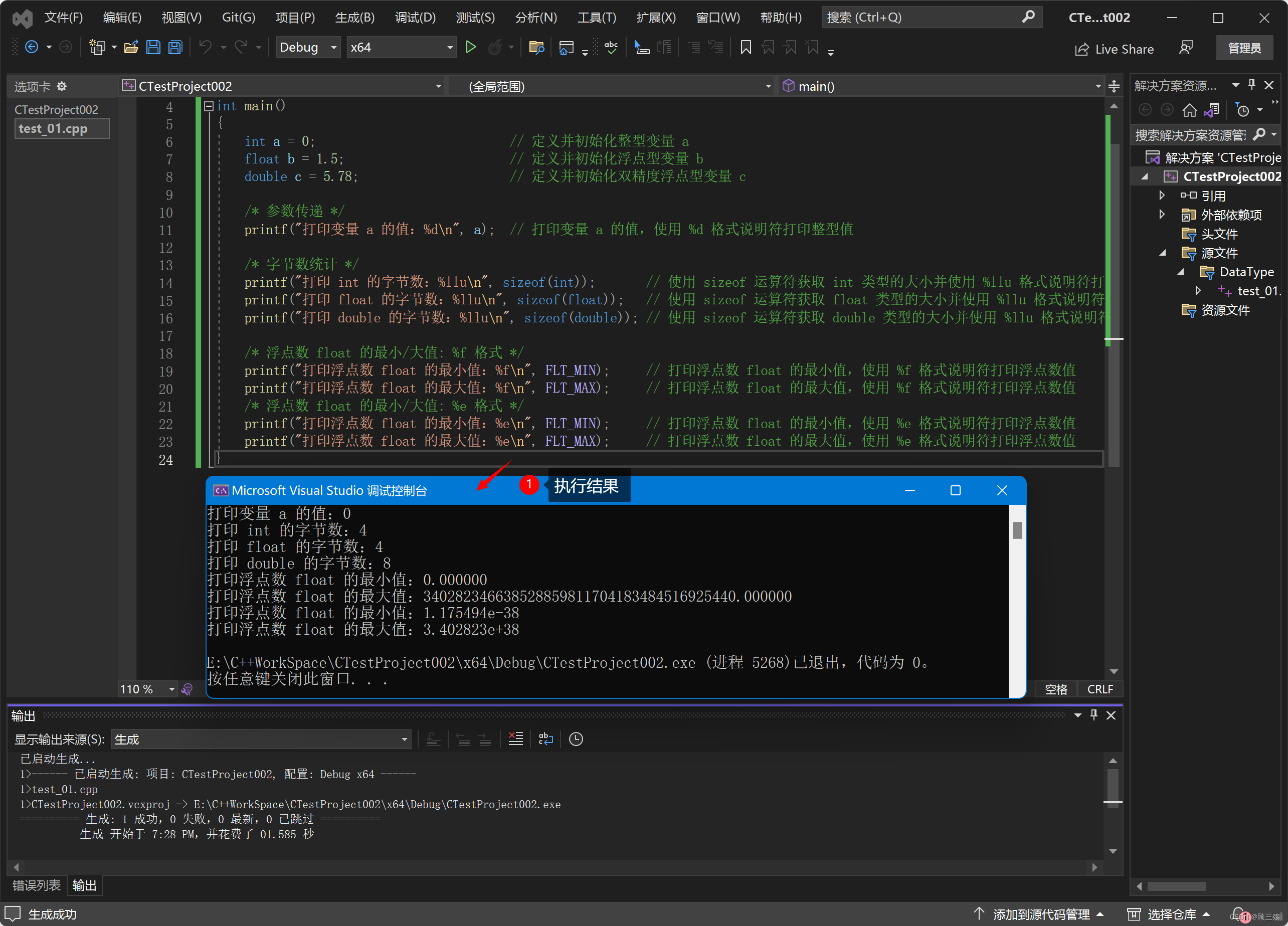
【C++ 程序设计】实战:C++ 变量实践练习题
目录 01. 变量:定义 02. 变量:初始化 03. 变量:参数传递 04. 变量:格式说明符 ① 占位符 “%d” 改为格式说明符 “%llu” ② 占位符 “%d” 改为格式说明符 “%f” 或 “%e” 05. 变量:字节数统计 06. 变量&a…...
微软对Visual Studio 17.7 Preview 4进行版本更新,新插件管理器亮相
近期微软发布了Visual Studio 17.7 Preview 4版本,而在这个版本当中,全新设计的扩展插件管理器将亮相,并且可以让用户可更简单地安装和管理扩展插件。 据了解,目前用户可以从 Visual Studio Marketplace 下载各式各样的 VS 扩展插…...
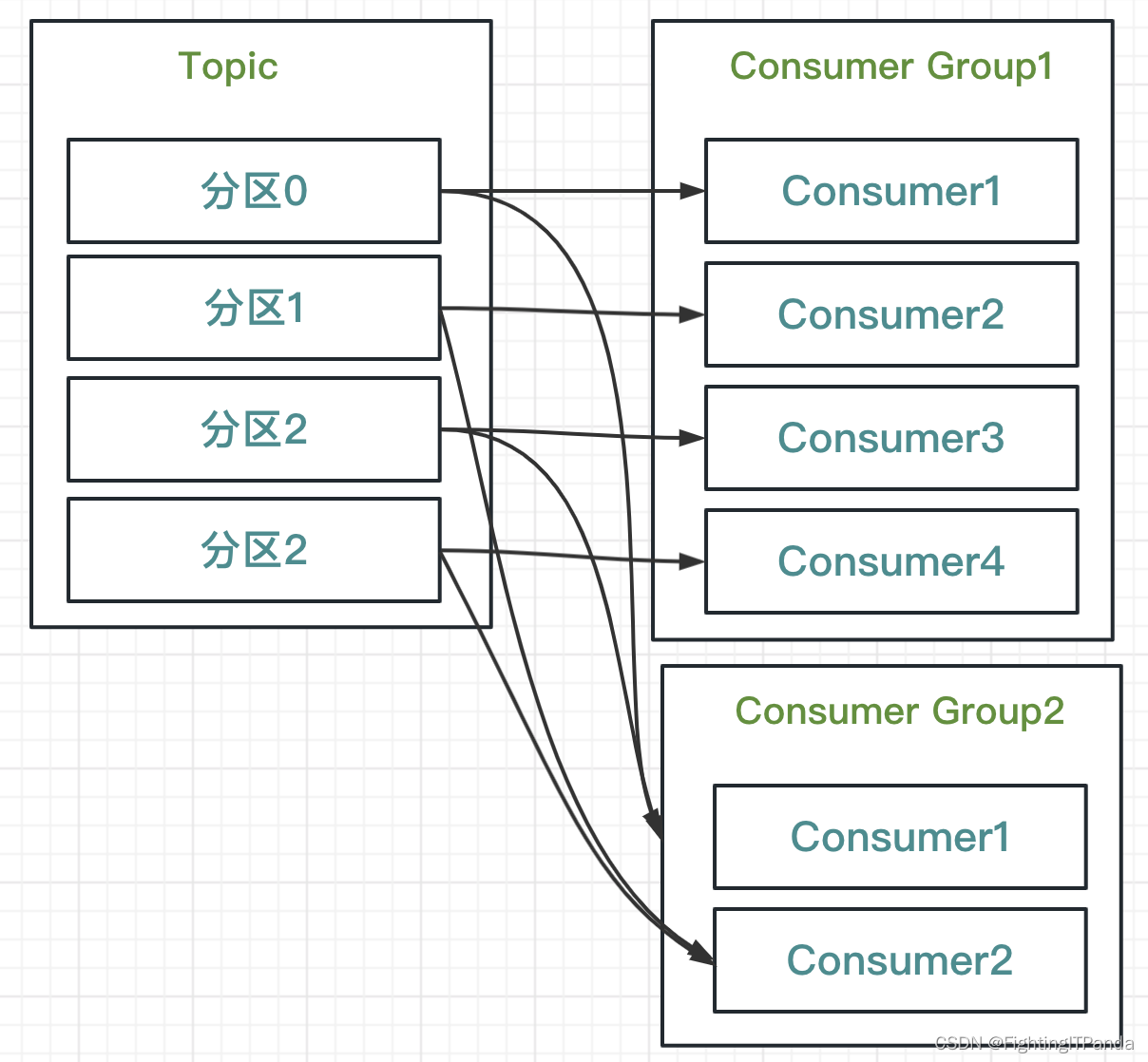
Kafka 入门到起飞 - Kafka怎么做到保障消息不会重复消费的? 消费者组是什么?
Kafka怎么做到避免消息重复消费的? 消费者组是什么? 消费者: 1、订阅Topic(主题) 2、从订阅的Topic消费(pull)消息, 3、将消费消息的offset(偏移量)保存在K…...

MongoDB 的增、查、改、删
Monogo使用 增 单条增加 db.member.insertOne({"name":"张三","age":18,"create":new Date()}) db.member.insert({"name":"李四1","age":18,"create":new Date()}) db.member.insertOne(…...

mysql常用操作命令
mysql常用操作命令 mysql:单进程多线程模型,一个SQL语句无法利用多个cpu core 一:基本命令 0.查看当前连接数 show global status like Thread$; show variables like "%timeout%"; show variables like "log_%";1.查看当前连接状态 show processlist…...

数学建模常见模型汇总
优化问题 线性规划、半定规划、几何规划、非线性规划、整数规划、多目标规划(分层序列法)、动态规划、存贮论、代理模型、响应面分析法、列生成算法 预测模型 微分方程、小波分析、回归分析、灰色预测、马尔可夫预测、时间序列分析(AR MAMA.RMA ARTMA LSTM神经网络)、混沌模…...
)
C#使用LINQ查询操作符实例代码(二)
目录 六、连表操作符 1、内连接2、左外连接(DefaultIfEmpty)3、组连接七、集合操作 八、分区操作符 1、Take():2、TakeWhile():3、Skip():4、SkipWhile():九、聚合操作符 1、Count: 返回集合项数。 2、LongCount&…...

jenkinsfile小试牛刀
序 本文主要演示一下如何用jenkinsfile来编译java服务 安装jenkins 这里使用docker来安装jenkins docker run --name jenkins-docker \ --volume $HOME/jenkins_home:/var/jenkins_home \ -p 8080:8080 jenkins/jenkins:2.416之后访问http://${yourip}:8080,然后…...

C++ xmake构建
文章目录 一、xmake.lua二、xmake常用语句 一、xmake.lua --xmake.luaset_project("XXX")add_rules("mode.debug", "mode.release") set_config("arch", "x64")if is_plat("windows") then -- the release modei…...
推荐带500创作模型的付费创作V2.1.0独立版系统源码
ChatGPT 付费创作系统 V2.1.0 提供最新的对应版本小程序端,上一版本增加了 PC 端绘画功能, 绘画功能采用其他绘画接口 – 意间 AI,本版新增了百度文心一言接口。 后台一些小细节的优化及一些小 BUG 的处理,前端进行了些小细节优…...
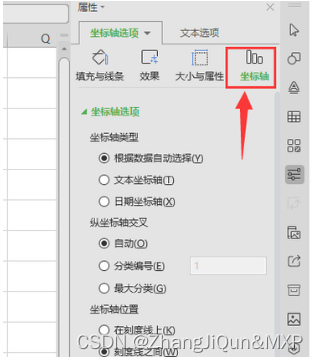
wps图表怎么改横纵坐标,MLP 多层感知器和CNN卷积神经网络区别
目录 wps表格横纵坐标轴怎么设置? MLP (Multilayer Perceptron) 多层感知器 CNN (Convolutional Neural Network) 卷积神经网络 多层感知器MLP,全连接网络,DNN三者的关系 wps表格横纵坐标轴怎么设置? 1、打开表格点击图的右侧…...

rdb和aof
RDB持久化:原理是将Redis在内存中的数据库记录定时dump到磁盘上的RDB持久化AOF持久化:原理是将Redis的操作日志以追加的方式写入文件 rdb: 开启方式:客户端可以通过向Redis服务器发送save或bgsave命令让服务器生成rdb文件&#…...
TCP网络通信编程之网络上传文件
【图片】 【思路解析】 【客户端代码】 import java.io.*; import java.net.InetAddress; import java.net.Socket; import java.net.UnknownHostException;/*** ProjectName: Study* FileName: TCPFileUploadClient* author:HWJ* Data: 2023/7/29 18:44*/ public class TCPFil…...

Java中对Redis的常用操作
目录 数据类型五种常用数据类型介绍各种数据类型特点 常用命令字符串操作命令哈希操作命令列表操作命令集合操作命令有序集合操作命令通用命令 在Java中操作RedisRedis的Java客户端Spring Data Redis使用方式介绍环境搭建配置Redis数据源编写配置类,创建RedisTempla…...

链路追踪设计
...

Golang之路---02 基础语法——常量 (包括特殊常量iota)
常量 //显式类型定义const a string "test" //隐式类型定义const b 20 //多个常量定义 const(c "test2"d 2.3e 27)iota iota是Golang语言的常量计数器,只能在常量表达式中使用 iota在const关键字出现时将被重置为0,const中每新…...

Pytest学习教程_装饰器(二)
前言 pytest装饰器是在使用 pytest 测试框架时用于扩展测试功能的特殊注解或修饰符。使用装饰器可以为测试函数提供额外的功能或行为。 以下是 pytest 装饰器的一些常见用法和用途: 装饰器作用pytest.fixture用于定义测试用例的前置条件和后置操作。可以创建可重…...
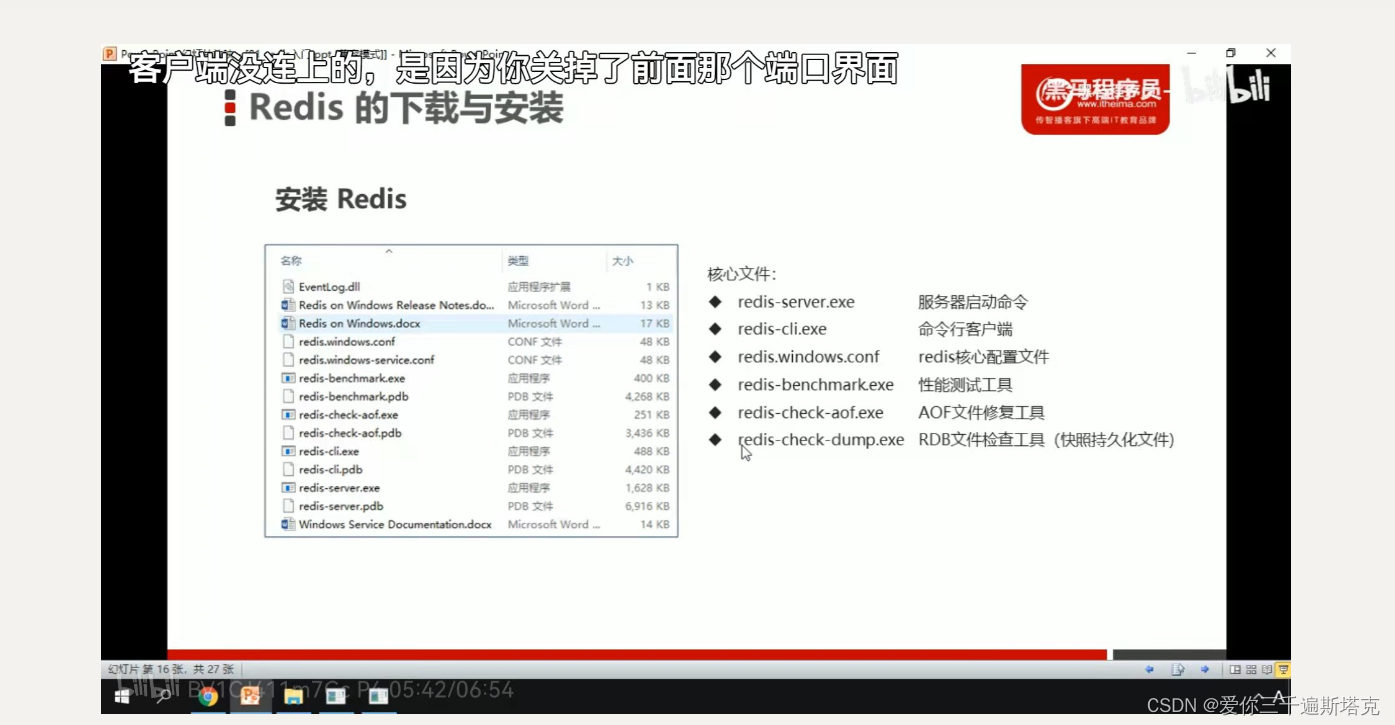
redis的如何使用
1、redis的使用 1.1windows安装 安装包下载地址:Releases dmajkic/redis GitHub 1.2 redis中常使用的几个文件 1.3 redis中运行 双击redis-server,既可以运行。 1.4使用redis客户单来连接redis 1.5redis的常用指标 redis-serve 服务端,端口号&am…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...
