排队理论简介
排队理论简介
- 1. 理论背景
- 2. 研究的数学方法
- 3. 拒绝型排队系统与等候型排队系统
- 4. 拒绝型排队系统
本文参考文献为Вентцель Е. С.的《Исследование операций》。
1. 理论背景
排队理论又称大众服务理论,顾名思义指的是在有限的服务条件下服务大量人员的一种理论情景。日常生活中常见的场景如,排队的电话亭、等待理发的顾客、售票窗口、商店结账处等等。
显然,这些排队情景中都有一些共性。如:
- 每个排队情景必然包括若干“服务人员”,称之为服务通道。一个排队情景中可以有一个或多个服务通道。
- 每个排队情景中必然也包括若干申请流(或称请求流),这些请求在某个随机时刻进入该排队系统。
- 当前正在处理的申请会占据一定的时间,在这段时间之后,处理该申请的通道会“放空”并等待处理下一个申请。
- 当有多余的申请等待处理时,该申请有2种情况:要么等待被处理,形成“队列”(即排队),要么离开该服务通道。
- 除4中的情况外,一个服务通道还可能处于非满载状态或停工状态。
一个服务通道能够成功处理的申请数,称为通过性。而排队理论研究的正是申请流、服务通道数量、服务通道的工作能力、排队系统的工作规则、工作效率等问题。
一般地,衡量一个排队系统的效率特征可以用以下的方式:
- 单位时间内可以处理的申请平均数量;
- 无法被满足、使排队系统无法服务的申请所占的百分比;
- 提交的申请能及时被处理的概率;
- 排队等候的平均用时;
- 等候用时的时长的分布律;
- 申请队列中的申请平均数量;
- 队列中申请数量的分布律;
- 单位时间内排队系统带来的平均收入。
2. 研究的数学方法
如果排队系统中的随机过程是马尔科夫过程,那么对排队系统的数学建模将会很简单。而如果排队系统中的过程确实是马尔科夫过程,那么逐个发生的事件流必须是泊松过程,即每个单独的事件都没有相应的后果或后续动作。对于排队过程来说,即需要申请流和服务流都满足泊松过程。然而业已证明,排队系统越复杂,服务通道越多,则越可以近似于马尔科夫过程。因此,采用马尔科夫过程研究排队理论并无大碍。
在研究排队过程之前,需要知道系统中的几个基本参数。
n n n – 服务通道数量;
λ \lambda λ – 申请流的强度;
μ \mu μ – 每个服务通道的处理能力(工作产能),即每个服务通道单位时间内可处理的申请的平均数量;
形成排队的条件(若存在)。
设排队系统中的申请流和服务流都是泊松过程,且为定常的,参数不随时间变化。而每2个事件之间的时间间隔 T T T是随机变量,其分布满足如下概率分布密度函数:
f ( t ) = λ e − λ t ( t > 0 ) f(t) = \lambda {\rm e}^{-\lambda t} \quad (t > 0) f(t)=λe−λt(t>0)
3. 拒绝型排队系统与等候型排队系统
排队系统分为2类:
- 拒绝型。当所有服务通道都被占用时,新的申请会被拒绝,离开排队系统并之后不再参与进来。
- 等候型。当所有服务通道都被占用时,新的申请加入等候队列。当某个通道处理完上一个申请变为空时,就从等候队列中转移一个申请至该通道并处理。
接下来将着重讲解拒绝型排队系统的数学模型。
4. 拒绝型排队系统
对于拒绝型排队系统来说,衡量其效率的指标称为绝对通过性,指的是单位时间内系统可以处理的申请的平均数量。与之对应的概念是相对通过性,指单位时间内被系统处理的申请的平均数,与该时间段内新增的申请数之比值。
设系统中有 n n n个服务通道。根据被占用的通道的个数,将系统的状态分为如下几类:
S 0 S_0 S0 – 所有服务通道都空;
S 1 S_1 S1 – 只有一个服务通道被占用,其他通道都空;
⋯ \cdots ⋯
S k S_k Sk – 有 k k k个通道被占用,其他通道都空;
⋯ \cdots ⋯
S n S_n Sn – 所有 n n n个通道都被占用。
如下图所示是拒绝型排队系统的示意图。

一开始系统中没有申请,所有服务通道为空,系统状态为 S 0 S_0 S0。当有一个申请加入时,占用一个服务通道,系统状态从 S 0 S_0 S0变为 S 1 S_1 S1,即 S 0 → S 1 S_0 \rightarrow S_1 S0→S1,此过程的强度(或密度)为 λ \lambda λ,可以理解为单位时间内新增了 λ \lambda λ个申请。以此类推,直到所有 n n n个通道均被占用。从低占用向高占用转化的过程中,每个状态转化的强度都是 λ \lambda λ。
当系统处于 S 1 S_1 S1状态,而该申请被完成时,系统将变成 S 0 S_0 S0状态,即 S 1 → S 0 S_1 \rightarrow S_0 S1→S0。此过程的强度(或密度)为 μ \mu μ,可以理解为一个被占用的服务通道单位时间内可以服务 μ \mu μ个申请。值得注意的是,从高占用向低占用转化的过程的强度并非全是 μ \mu μ,如图所示, S k + 1 → S k S_{k+1} \rightarrow S_k Sk+1→Sk过程的强度为 ( k + 1 ) μ \left( k+1 \right) \mu (k+1)μ。
利用柯尔莫哥洛夫方程,对图中每个状态的“入量”和“出量”进行描述,可以得到每个状态的柯尔莫哥洛夫方程。如,对于某个状态 S k S_k Sk来说,其“出量”(即图中从方块 S k S_k Sk发出的箭头)有两个,分别是方块 S k S_k Sk右上的 λ \lambda λ和左下的 k μ k \mu kμ;而“入量”(即图中进入方块 S k S_k Sk的箭头)也有2个,分别是方块 S k S_k Sk左上的 λ \lambda λ和右下的 ( k + 1 ) μ (k+1) \mu (k+1)μ。那么,状态 S k S_k Sk的概率可以描述为
d p k d t = − ( λ + k μ ) p k + λ p k − 1 + ( k + 1 ) μ p k + 1 \frac{ {\rm d} p_k }{ {\rm d} t } = -\left( \lambda + k \mu \right) p_k + \lambda p_{k-1} + (k+1) \mu p_{k+1} dtdpk=−(λ+kμ)pk+λpk−1+(k+1)μpk+1上式的含义是:
- 所有方块 S k S_k Sk的出量均为负项,而入量为正项;
- 出量有2个:1) 右上的 λ \lambda λ从 S k S_k Sk出发,其概率为 p k p_k pk,故该项是 − λ p k -\lambda p_k −λpk;2) 左下的 k μ k \mu kμ也从 S k S_k Sk出发,其概率也是 p k p_k pk,故该项是 − k μ p k -k \mu p_k −kμpk。
- 入量有2个:1) 右下的 ( k + 1 ) μ (k+1) \mu (k+1)μ从上一个状态 S k + 1 S_{k+1} Sk+1出发,其概率对应是 p k + 1 p_{k+1} pk+1,故该项是 ( k + 1 ) μ p k + 1 (k+1) \mu p_{k+1} (k+1)μpk+1;2) 左上的 λ \lambda λ从上一个状态 S k − 1 S_{k-1} Sk−1出发,其概率对应是 p k − 1 p_{k-1} pk−1,故该项是 λ p k − 1 \lambda p_{k-1} λpk−1。
- 注意:从哪个方块 S i S_i Si出发,概率 p i p_i pi的下标就要和方块的下标对应!概率 p i p_i pi取决于箭头的出发地而不是指向地!
由此可以写出图中的微分方程关系:
d p 0 d t = − λ p 0 + μ p 1 d p 1 d t = − ( λ + μ ) p 1 + λ p 0 + 2 μ p 1 ⋮ d p k d t = − ( λ + k μ ) p k + λ p k − 1 + ( k + 1 ) μ p k + 1 ⋮ d p n d t = − n μ p n + λ p n − 1 (1) \begin{aligned} \frac{ {\rm d} p_0 }{ {\rm d} t } &= - \lambda p_0 + \mu p_1 \\ \frac{ {\rm d} p_1 }{ {\rm d} t } &= - \left( \lambda + \mu \right) p_1 + \lambda p_0 + 2\mu p_1 \\ \vdots \\ \frac{ {\rm d} p_k }{ {\rm d} t } &= - \left( \lambda + k\mu \right) p_k + \lambda p_{k-1} + (k+1) \mu p_{k+1} \\ \vdots \\ \frac{ {\rm d} p_n }{ {\rm d} t } &= - n\mu p_n + \lambda p_{n-1} \\ \tag{1} \end{aligned} dtdp0dtdp1⋮dtdpk⋮dtdpn=−λp0+μp1=−(λ+μ)p1+λp0+2μp1=−(λ+kμ)pk+λpk−1+(k+1)μpk+1=−nμpn+λpn−1(1)上述方程称为艾拉姆咖方程。初始条件为
p 0 ( 0 ) = 1 , p 1 ( 0 ) = p 2 ( 0 ) = ⋯ = p n ( 0 ) = 0 p_0 (0) = 1, \qquad p_1(0) = p_2(0) = \cdots = p_n(0) = 0 p0(0)=1,p1(0)=p2(0)=⋯=pn(0)=0艾拉姆咖方程往往无法手解,需要通过计算机辅助求解,得到结果 p i ( t ) p_i(t) pi(t)为每种状态出现的概率。
另外,在实际运用中往往还感兴趣状态的边界概率,指系统的稳态模式下的概率。这里不加推导地给出公式:
p k = λ k μ ⋅ 2 μ ⋯ k μ p 0 = ( λ / μ ) k k ! p 0 p 0 = 1 1 + λ / μ 1 ! + ( λ / μ ) 2 2 ! + ⋯ + ( λ / μ ) n n ! p_k = \frac{\lambda^k}{\mu \cdot 2\mu \cdots k\mu} p_0 = \frac{ \left( \lambda / \mu \right)^k}{k!} p_0 \\ p_0 = \frac{1}{ 1 + \frac{\lambda / \mu}{1!} + \frac{ \left( \lambda / \mu \right)^2}{2!} + \cdots + \frac{ \left( \lambda / \mu \right)^n}{n!} } pk=μ⋅2μ⋯kμλkp0=k!(λ/μ)kp0p0=1+1!λ/μ+2!(λ/μ)2+⋯+n!(λ/μ)n1记 λ / μ = ρ \lambda / \mu = \rho λ/μ=ρ称为换算强度,其物理意义是:在处理一个请求的平均时长内,到来(新增)的请求的平均数量。
则上述边界概率公式可改写为
p k = ρ k k ! p 0 p_k = \frac{\rho^k}{k!} p_0 pk=k!ρkp0 p 0 = 1 1 + ρ 1 ! + ρ 2 2 ! + ⋯ + ρ n n ! (2) p_0 = \frac{1}{ 1 + \frac{\rho}{1!} + \frac{ \rho^2}{2!} + \cdots + \frac{ \rho^n}{n!} } \tag{2} p0=1+1!ρ+2!ρ2+⋯+n!ρn1(2)式(2)同样称为艾拉姆咖方程。
显然,所有通道都被占用的概率是 p n p_n pn,那么“新增申请能够被处理”的概率为
q = 1 − p n q = 1 - p_n q=1−pn进而绝对通过性为
A = λ q = λ ( 1 − p n ) A = \lambda q = \lambda \left(1 - p_n \right) A=λq=λ(1−pn)则繁忙通道的平均个数 k ˉ \bar k kˉ可以表示为加权和:
k ˉ = 0 ⋅ p 0 + 1 ⋅ p 1 + ⋯ + n ⋅ p n \bar k = 0 \cdot p_0 + 1 \cdot p_1 + \cdots + n \cdot p_n kˉ=0⋅p0+1⋅p1+⋯+n⋅pn即为数学期望。
另一方面,由于绝对通过性表示单位时间内处理的申请的平均数量,而一个被占用的服务通道在单位时间内可以处理 μ \mu μ个申请,故繁忙通道的平均个数亦可表示为
k ˉ = A μ = λ ( 1 − p n ) μ = ρ ( 1 − p n ) \bar k = \frac{A}{\mu} = \frac{ \lambda \left(1 - p_n \right) }{\mu} = \rho \left( 1 - p_n\right) kˉ=μA=μλ(1−pn)=ρ(1−pn)
相关文章:

排队理论简介
排队理论简介 1. 理论背景2. 研究的数学方法3. 拒绝型排队系统与等候型排队系统4. 拒绝型排队系统 本文参考文献为Вентцель Е. С.的《Исследование операций》。 1. 理论背景 排队理论又称大众服务理论,顾名思义指的是在有限的服务条…...
-算法分析)
极速查找(3)-算法分析
篇前小言 本篇文章是对查找(2)的续讲二叉排序树 二叉排序树(Binary Search Tree,BST),又称为二叉查找树,是一种特殊的二叉树。性质: 左子树的节点值小于根节点的值,右…...

http 常见的响应状态码 ?
100——客户必须继续发出请求101——客户要求服务器根据请求转换HTTP协议版本200——交易成功201——提示知道新文件的URL202——接受和处理、但处理未完成203——返回信息不确定或不完整204——请求收到,但返回信息为空205——服务器完成了请求,用户代理…...
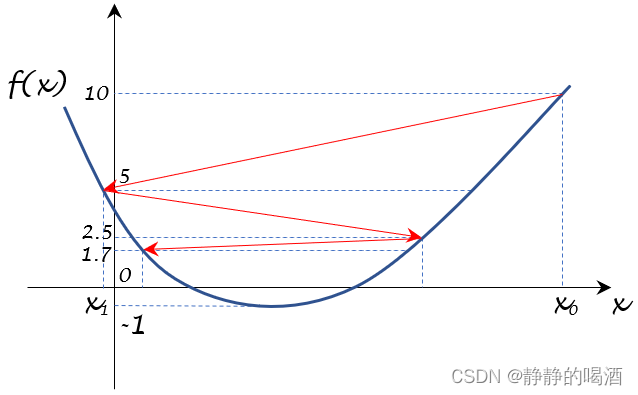
机器学习笔记之优化算法(四)线搜索方法(步长角度;非精确搜索)
机器学习笔记之优化算法——线搜索方法[步长角度,非精确搜索] 引言回顾:精确搜索步长及其弊端非精确搜索近似求解最优步长的条件反例论述 引言 上一节介绍了从精确搜索的步长角度观察了线搜索方法,本节将从非精确搜索的步长角度重新观察线搜…...
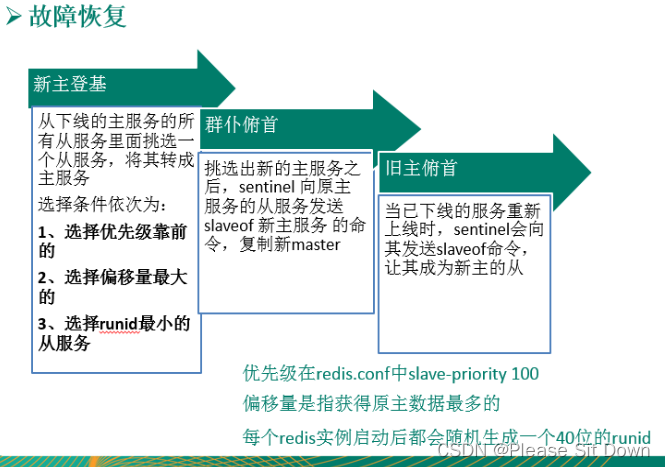
Redis 哨兵 (sentinel)
是什么 官网理论:https://redis.io/docs/management/sentinel/ 吹哨人巡查监控后台 master 主机是否故障,如果故障了根据投票数自动将某一个从库转换为新主库,继续对外服务。 作用:无人值守运维 哨兵的作用: 1…...

统计2021年10月每个退货率不大于0.5的商品各项指标
统计2021年10月每个退货率不大于0.5的商品各项指标_牛客题霸_牛客网s mysql(ifnull): select product_id, format(ifnull(sum(if_click)/nullif(count(*),0),0),3) as ctr, format(ifnull(sum(if_cart)/nullif(sum(if_click),0),0),3) as c…...
【小波尺度谱】从分段离散小波变换计算小波尺度谱研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
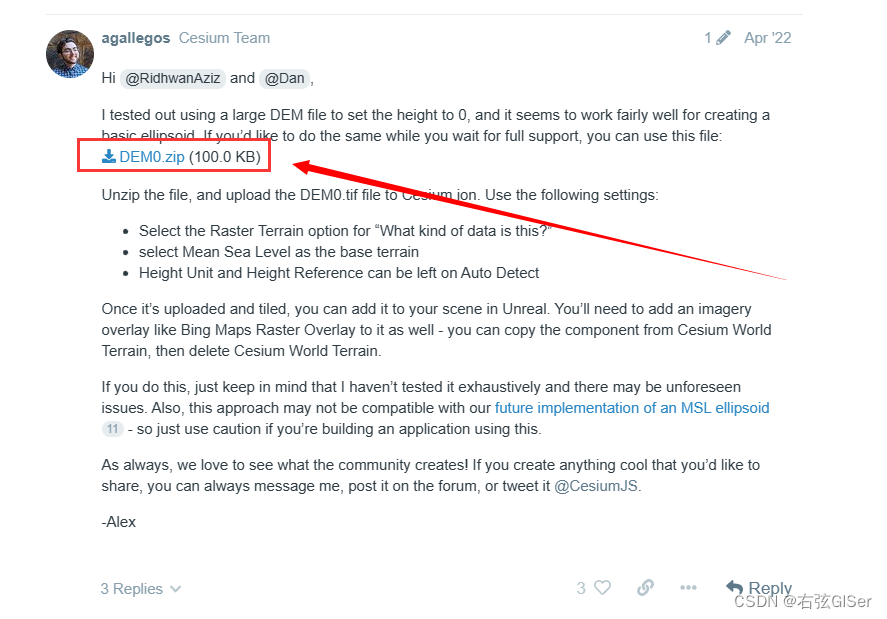
UE5、CesiumForUnreal加载无高度地形
文章目录 1.实现目标2.实现过程3.参考资料1.实现目标 在UE5中,CesiumForUnreal插件默认的地形都是带高度的,这里加载没有高度的地形,即大地高程为0,GIF动图如下: 2.实现过程 参考官方的教程,下载无高度的DEM,再切片加载到UE中。 (1)下载无高度地形DEM0。 在官方帖子…...

关于Spring中的@Configuration中的proxyBeanMethods属性
Configuration的proxyBeanMethods属性 在Configuration注解中,有两个属性: value配置Bean名称proxyBeanMethos,默认是true 这个proxyBeanMethods的默认属性是true。 直接说:当Configuration注解的proxyBeanMeathods属性是true…...

dp1,ACM暑期培训
D - 摆花 P1077 [NOIP2012 普及组] 摆花 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) Description 小明的花店新开张,为了吸引顾客,他想在花店的门口摆上一排花,共 m 盆。通过调查顾客的喜好,小明列出了顾客最喜欢的 n 种花&…...

大厂程序员的水平比非大厂高很多嘛?
最近一个月,筛选了一百多份简历,前前后后面试了二三十人,基本上都是有大厂经历的人。同时,也录用了几个有大厂经历的。但整体而言,打破了对大厂出来的都是优质人才的幻觉。看到的实际情况与想象中的落差还是比较大的。…...
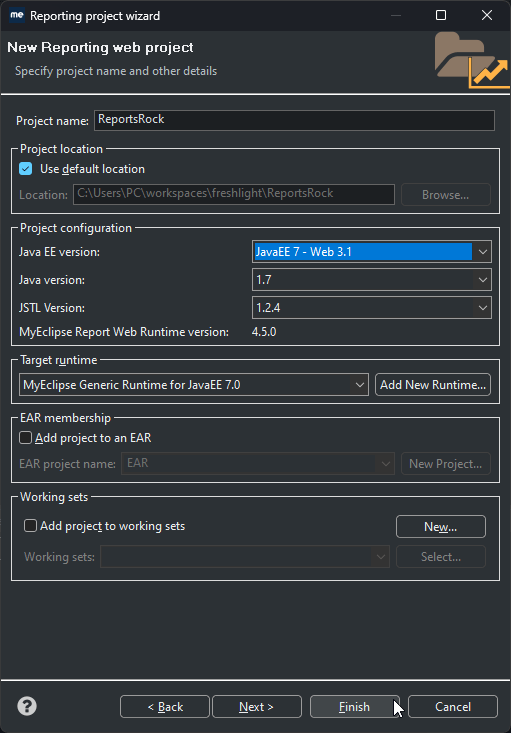
Java开发工具MyEclipse发布v2023.1.2,今年第二个修复版!
MyEclipse一次性提供了巨量的Eclipse插件库,无需学习任何新的开发语言和工具,便可在一体化的IDE下进行Java EE、Web和PhoneGap移动应用的开发;强大的智能代码补齐功能,让企业开发化繁为简。 MyEclipse v2023.1.2官方正式版下载 …...
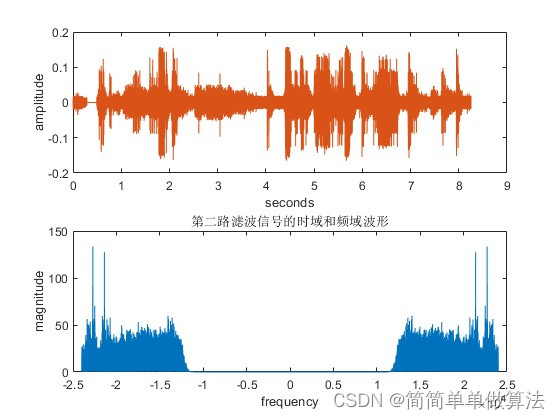
基于正交滤波器组的语音DPCM编解码算法matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 matlab2022a 3.部分核心程序 ...........................................................g0zeros(1,lenH); g1zeros(1,l…...
VS2022和QT混合编程打包发布程序
1.在开始菜单输入 CMD 找到 Qt5.15.2(MSVC 64-bit) 2.输入windeployqt exe所在路径 3.运行完毕后,双击打开exe文件,可能会报错,缺少相关的dll,找到缺少的dll拷贝到运行文件夹下即可。...

Filebeat学习笔记
Filebeat基本概念 简介 Filebeat是一种轻量级日志采集器,内置有多种模块(auditd、Apache、Nginx、System、MySQL等),针对常见格式的日志大大简化收集、解析和可视化过程,只需一条命令即可。之所以能实现这一点&#…...
 —— React17+React Hook+TS4 最佳实践,仿 Jira 企业级项目(十六))
【实战】 九、深入React 状态管理与Redux机制(一) —— React17+React Hook+TS4 最佳实践,仿 Jira 企业级项目(十六)
文章目录 一、项目起航:项目初始化与配置二、React 与 Hook 应用:实现项目列表三、TS 应用:JS神助攻 - 强类型四、JWT、用户认证与异步请求五、CSS 其实很简单 - 用 CSS-in-JS 添加样式六、用户体验优化 - 加载中和错误状态处理七、Hook&…...

第九十五回 如何使用dio的转换器
文章目录 概念介绍使用方法使用默认的转换器自定义转换器 示例代码经验分享 我们在上一章回中介绍了"如何打造一个网络框架"相关的内容,本章回中将介绍 如何使用dio的转换器.闲话休提,让我们一起Talk Flutter吧。 概念介绍 转换器主要用来转…...

Python深度学习“四大名著”之一【赠书活动|第二期《Python机器学习:基于PyTorch和Scikit-Learn》】
近年来,机器学习方法凭借其理解海量数据和自主决策的能力,已在医疗保健、 机器人、生物学、物理学、大众消费和互联网服务等行业得到了广泛的应用。自从AlexNet模型在2012年ImageNet大赛被提出以来,机器学习和深度学习迅猛发展,取…...
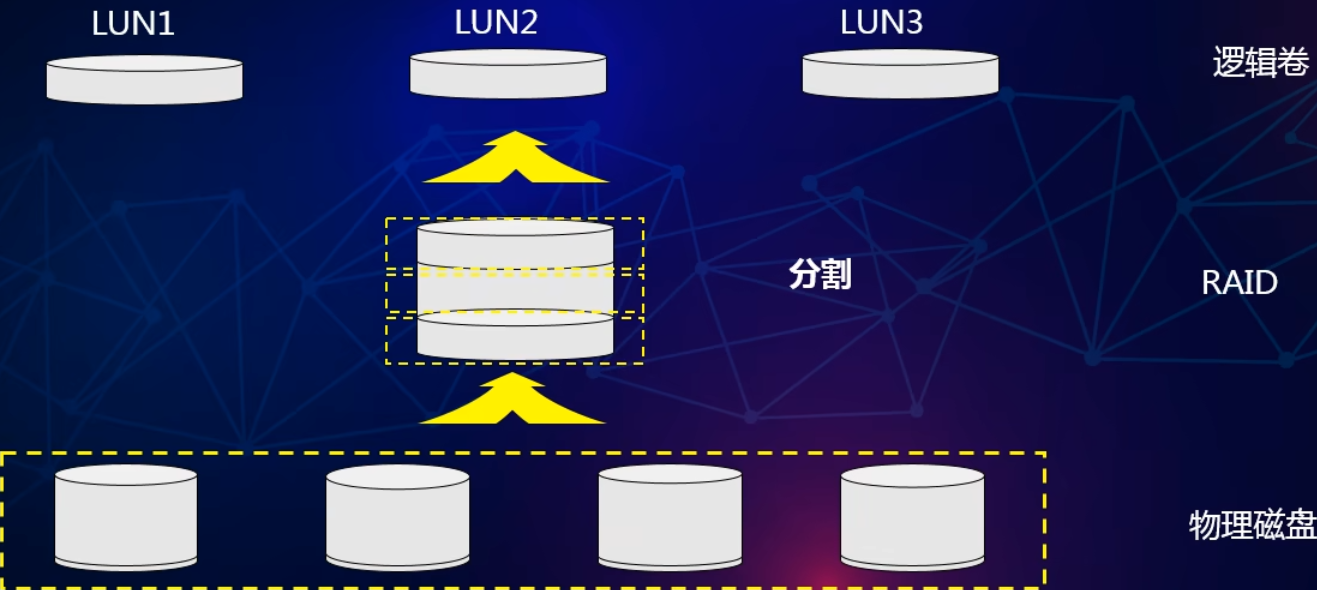
RAID相关知识
简介 RAID ( Redundant Array of Independent Disks )即独立磁盘冗余阵列,通常简称为磁盘阵列。RAID技术将多个单独的物理硬盘以不同的方式组合成一个逻辑磁盘,从而提高硬盘的读写性能和数据安全性。 数据组织形式 分块&#x…...
DataStructure--Basic
程序设计数据结构算法 只谈数据结构不谈算法就跟去话剧院看梁山伯与祝英台结果只有梁山伯在演,祝英台生病了没来一样。 本文的所有内容都出自《大话数据结构》这本书中的代码实现部分,建议看书,书中比我本文写的全。 数据结构,直…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...
