Informer 论文学习笔记
论文:《Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting》
代码:https://github.com/zhouhaoyi/Informer2020
地址:https://arxiv.org/abs/2012.07436v3
特点:
- 实现时间与空间复杂度为 O ( L ln L ) \mathcal{O}(L\ln L) O(LlnL) 的自注意力;
- 使用自注意力提纯(Distilling)的方法,降低了特征的冗余;
- 以生成式的风格一次性输出长序列预测结果,杜绝了 One-by-One 方式中存在的误差积累;
- 基于上面的内容,创建新的 LSTF 模型 Informer。
核心贡献:
- 用新的自注意力模块 ProbSparse Self-Attention 降低了原始 Self-Attention 的时间与空间复杂度;
- 提出 Self-Attention 净化(Distilling) 方法,进一步降低模型整体的复杂度;
Informer 模型的整体结构
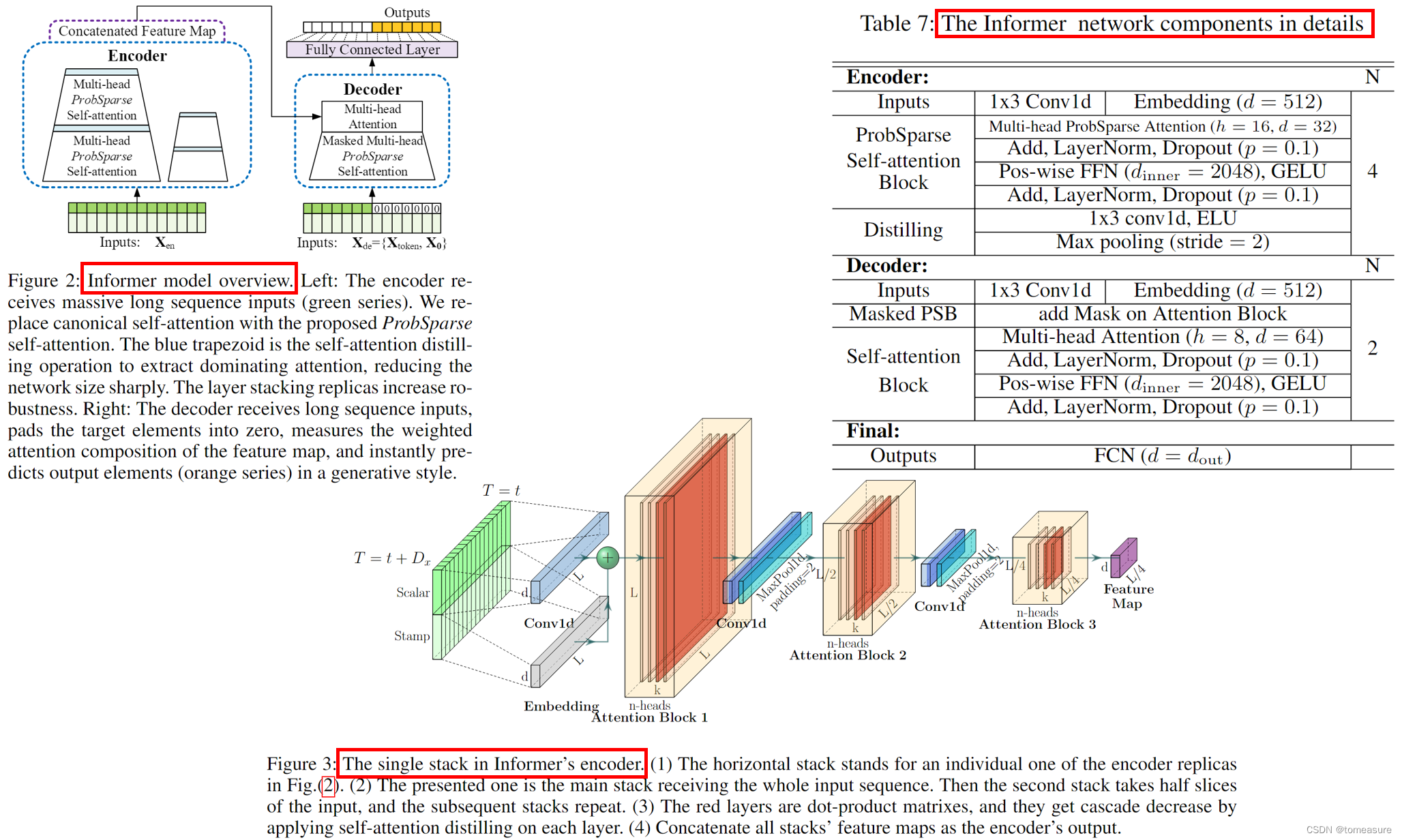
ProbSparse Self-Attention
先介绍一下算法的整体流程,后面再介绍具体含义和原因。
Require:Tensor Q ∈ R m × d , K ∈ R n × d , V ∈ R n × d \pmb{Q}\in\mathbb{R}^{m\times d},\pmb{K}\in\mathbb{R}^{n\times d},\pmb{V}\in\mathbb{R}^{n\times d} Q∈Rm×d,K∈Rn×d,V∈Rn×d
- print set hyperparameter c c c, u = c ln m u=c\ln m u=clnm and U = m ln n U=m\ln n U=mlnn
- randomly select U U U dot-product pairs from K \pmb{K} K to K ˉ \bar{\pmb{K}} Kˉ
- set the sample score S ˉ = Q K ˉ T \bar{\pmb{S}}=\pmb{Q}\bar{\pmb{K}}^T Sˉ=QKˉT
- compute the measurement M = max ( S ˉ ) − mean ( S ˉ ) M=\max(\bar{\pmb{S}})-\text{mean}(\bar{\pmb{S}}) M=max(Sˉ)−mean(Sˉ) by row
- set Top- u \text{Top-}u Top-u queries under M M M as Q ˉ \bar{\pmb{Q}} Qˉ
- set S 1 = softmax ( Q ˉ K T / d ) ⋅ V \pmb{S}_1=\text{softmax}(\bar{\pmb{Q}}\pmb{K}^T/\sqrt{d})\cdot \pmb{V} S1=softmax(QˉKT/d)⋅V
- set S 0 = mean ( V ) \pmb{S}_0=\text{mean}(\pmb{V}) S0=mean(V)
- set S = { S 1 , S 0 } \pmb{S}=\{\pmb{S}_1,\pmb{S}_0\} S={S1,S0} by their original rows accordingly
Ensure:self-attention feature map S \pmb{S} S
ProbSparse Self-Attention 的基本思想
利用原始 Self-Attention 中的稀疏性,降低算法的时间与空间复杂度。
核心方法:利用下式选出对 value 更有价值的 query
M ˉ ( q i , K ) = max j { q i k j T d } − 1 L K Σ j = 1 L K q i k j T d \bar{M}(\pmb{q}_i,\pmb{K})=\max_{j}\{\frac{\pmb{q}_i\pmb{k}_j^T}{\sqrt{d}}\}-\frac{1}{L_K}\Sigma^{L_K}_{j=1}\frac{\pmb{q}_i\pmb{k}_j^T}{\sqrt{d}} Mˉ(qi,K)=jmax{dqikjT}−LK1Σj=1LKdqikjT
即算法中的 3 与 4。
为什么用这种方法?:
原始 Self-Attention softmax ( Q K T / d ) ⋅ V \text{softmax}(\pmb{Q}\pmb{K}^T/\sqrt{d})\cdot \pmb{V} softmax(QKT/d)⋅V 可改写为下面的概率形式:
A ( q i , K , V ) = Σ j k ( q i , k j ) Σ l k ( q i , k l ) v j = E p ( k j ∣ q i ) [ v j ] \mathcal{A}(\pmb{q}_i,\pmb{K},\pmb{V})=\Sigma_j\frac{k(\pmb{q}_i,\pmb{k}_j)}{\Sigma_l k(\pmb{q}_i,\pmb{k}_l)}\pmb{v}_j=\mathbb{E}_{p(\pmb{k}_j|\pmb{q}_i)}[\pmb{v}_j] A(qi,K,V)=ΣjΣlk(qi,kl)k(qi,kj)vj=Ep(kj∣qi)[vj]
k ( ⋅ , ⋅ ) k(\cdot,\cdot) k(⋅,⋅) 的含义不再赘述。
为度量 query 的稀疏性,可以考虑 p ( k j ∣ q i ) p(\pmb{k}_j|\pmb{q}_i) p(kj∣qi) 与均匀分布 q ( k j ∣ q i ) = 1 / L K q(\pmb{k}_j|\pmb{q}_i)=1/L_K q(kj∣qi)=1/LK`之间的 KL 散度 K L ( q ∣ ∣ p ) = − Σ 1 L K ln ( k ( q i , k j ) Σ l k ( q i , k l ) L K ) KL(q||p)=-\Sigma\frac{1}{L_K}\ln(\frac{k(\pmb{q}_i,\pmb{k}_j)}{\Sigma_l k(\pmb{q}_i,\pmb{k}_l)}L_K) KL(q∣∣p)=−ΣLK1ln(Σlk(qi,kl)k(qi,kj)LK),展开并舍弃常数项之后可得第 i 个 query 的稀疏性度量为:
M ( q i , K ) = ln Σ j = 1 L K e q i k j T d − 1 L K Σ j = 1 L K q i k j T d M(\pmb{q}_i,\pmb{K})=\ln\Sigma^{L_K}_{j=1}e^{\frac{\pmb{q}_i\pmb{k}^T_j}{\sqrt{d}}}-\frac{1}{L_K}\Sigma^{L_K}_{j=1}\frac{\pmb{q}_i\pmb{k}^T_j}{\sqrt{d}} M(qi,K)=lnΣj=1LKedqikjT−LK1Σj=1LKdqikjT
基于 M,可以选用 Top-u 的 queries 构成的 Q ˉ \bar{\pmb{Q}} Qˉ 代替 Q 计算自注意力(文中设置 u = c ln L Q u=c\ln L_Q u=clnLQ,其中 c 是超参数)。
为什么要使用这两个分布的 KL 散度?为什么M可以度量注意力的稀疏性?:Self-Attention 涉及到了点积运算,该运算表明 p ( k j ∣ q i ) p(\pmb{k}_j|\pmb{q}_i) p(kj∣qi) 与均匀分布 q ( k j ∣ q i ) = 1 / L K q(\pmb{k}_j|\pmb{q}_i)=1/L_K q(kj∣qi)=1/LK 之间的差别越大越好,这启发我们使用 M 作为稀疏性的度量。
新问题:M 中的第一项实际计算时的复杂度仍旧是 O ( L 2 ) \mathcal{O}(L^2) O(L2) 的。
解决方式:基于 Lemma 1 与 Proposition 1,先随机采样 U = L K ln L Q U=L_K\ln L_Q U=LKlnLQ 个 k-q 对,然后在这 U 个 k-q 对上计算 M ˉ = max j { q i k j T d } − mean j { q i k j T d } \bar{M}=\max_{j}\{\frac{\pmb{q}_i\pmb{k}^T_j}{\sqrt{d}}\}-\text{mean}_{j}\{\frac{\pmb{q}_i\pmb{k}^T_j}{\sqrt{d}}\} Mˉ=maxj{dqikjT}−meanj{dqikjT} 作为 M 的近似值,最后选定 top-u 个 query 用作 Self-Attention 计算。(即算法中的 1、2、5 和 6,这里两次降低计算量)补充:
- Lemma 1:For each query q i ∈ R d \pmb{q}_i\in\mathbb{R}^d qi∈Rd and k j ∈ R d \pmb{k}_j\in\mathbb{R}^d kj∈Rd in the keys set K \pmb{K} K, we have the bound as ln L K ≤ M ( q i , K ) ≤ ln L K + M ˉ ( q i , K ) \ln L_K\leq M(\pmb{q}_i,\pmb{K})\leq\ln L_K +\bar{M}(\pmb{q}_i,\pmb{K}) lnLK≤M(qi,K)≤lnLK+Mˉ(qi,K). When q i ∈ K \pmb{q}_i\in\pmb{K} qi∈K, it also holds.(它说明可以用 M ˉ \bar{M} Mˉ 做近似计算。利用凸函数证明)
- Proposition 1: Assuming k j ∼ N ( μ , Σ ) \pmb{k}_j\sim\mathcal{N}(\mu,\Sigma) kj∼N(μ,Σ) and we let q k i \pmb{q}\pmb{k}_i qki denote set { ( q i k j T ) / d ∣ j = 1 , ⋯ , L K } \{(\pmb{q}_i\pmb{k}_j^T)/\sqrt{d}|j=1,\cdots,L_K\} {(qikjT)/d∣j=1,⋯,LK}, then ∀ M m = max i M ( q i , K ) \forall M_m=\max_i M(\pmb{q}_i,\pmb{K}) ∀Mm=maxiM(qi,K) there exist κ > 0 \kappa>0 κ>0 such that: in the interval ∀ q 1 , q 2 ∈ { q ∣ M ( q , K ) ∈ [ M m , M m − κ ) } \forall\pmb{q}_1,\pmb{q}_2\in\{\pmb{q}|M(\pmb{q},\pmb{K})\in[M_m,M_m-\kappa)\} ∀q1,q2∈{q∣M(q,K)∈[Mm,Mm−κ)}, if M ˉ ( q 1 , K ) > M ˉ ( q 2 , K ) \bar{M}(\pmb{q}_1,\pmb{K})>\bar{M}(\pmb{q}_2,\pmb{K}) Mˉ(q1,K)>Mˉ(q2,K) and Var ( q k 1 ) > Var ( q k 2 ) \text{Var}(\pmb{q}\pmb{k}_1)>\text{Var}(\pmb{q}\pmb{k}_2) Var(qk1)>Var(qk2), we have high probability that M ( q 1 , K ) > M ( q 2 , K ) M(\pmb{q}_1,\pmb{K})>M(\pmb{q}_2,\pmb{K}) M(q1,K)>M(q2,K).(采样后不影响排序,这说明采样之后仍旧可以保证 Top-u 的可靠性。利用对数正态分布及数值化样例定性式证明)
Self-Attention Distilling
目的:在自注意力模块之后,过滤掉 value 中的冗余信息。
方式:使用 CNN、MaxPooling 进行下采样:
\pmb{X}^t_{j+1}=\text{MaxPool}(\text{ELU}(\text{Conv1d}([\pmb{X}^t_j]_{AB})))
其中,CNN 的 kernel-size=3,pooling 的 stride=2,整体的空间复杂度为: O ( ( 2 − ϵ ) L log L ) \mathcal{O}((2-\epsilon)L\log L) O((2−ϵ)LlogL), ϵ \epsilon ϵ 是一个小量(原因是: 1 + 1 2 + 1 4 + 1 8 + ⋯ 1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdots 1+21+41+81+⋯)。
其他
- Decoder:与原始 Transformer 的一致;
- 生成式推断(Generative Inference):一次性输出长序列预测结果,而非迭代地逐个输出结果。
- Loss Function:MSE
- 位置嵌入(Position Embedding):局部时间戳的位置嵌入(PE,使用sin函数)、全局时间戳的位置嵌入(SE,用于日月周节日等特殊时间点) PE ( L x × ( t − 1 ) + i , ) + Σ [ SE ( L x × ( t − 1 ) + i ) ] p \text{PE}_{(L_x\times(t-1)+i,)}+\Sigma[\text{SE}_{(L_x\times(t-1)+i)}]_p PE(Lx×(t−1)+i,)+Σ[SE(Lx×(t−1)+i)]p
# PE pe[:, 0::2] = torch.sin(position * div_term) pe[:, 1::2] = torch.cos(position * div_term) # SE minute_x = nn.Embedding( 4, d_model)(x[:,:,4]) hour_x = nn.Embedding(24, d_model)(x[:,:,3]) weekday_x = nn.Embedding( 7, d_model)(x[:,:,2]) day_x = nn.Embedding(32, d_model)(x[:,:,1]) month_x = nn.Embedding(13, d_model)(x[:,:,0]) se = hour_x + weekday_x + day_x + month_x + minute_x
相关文章:

Informer 论文学习笔记
论文:《Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting》 代码:https://github.com/zhouhaoyi/Informer2020 地址:https://arxiv.org/abs/2012.07436v3 特点: 实现时间与空间复杂度为 O ( …...

c语言位段知识详解
本篇文章带来位段相关知识详细讲解! 如果您觉得文章不错,期待你的一键三连哦,你的鼓励是我创作的动力之源,让我们一起加油,一起奔跑,让我们顶峰相见!!! 目录 一.什么是…...
FFmpeg aresample_swr_opts的解析
ffmpeg option的解析 aresample_swr_opts是AVFilterGraph中的option。 static const AVOption filtergraph_options[] {{ "thread_type", "Allowed thread types", OFFSET(thread_type), AV_OPT_TYPE_FLAGS,{ .i64 AVFILTER_THREAD_SLICE }, 0, INT_MA…...

CAN学习笔记3:STM32 CAN控制器介绍
STM32 CAN控制器 1 概述 STM32 CAN控制器(bxCAN),支持CAN 2.0A 和 CAN 2.0B Active版本协议。CAN 2.0A 只能处理标准数据帧且扩展帧的内容会识别错误,而CAN 2.0B Active 可以处理标准数据帧和扩展数据帧。 2 bxCAN 特性 波特率…...

软工导论知识框架(二)结构化的需求分析
本章节涉及很多重要图表的制作,如ER图、数据流图、状态转换图、数据字典的书写等,对初学者来说比较生僻,本贴只介绍基础的轮廓,后面会有单独的帖子详解各图表如何绘制。 一.结构化的软件开发方法:结构化的分析、设计、…...

[SQL挖掘机] - 算术函数 - abs
介绍: 当谈到 SQL 中的 abs 函数时,它是一个用于计算数值的绝对值的函数。“abs” 代表 “absolute”(绝对),因此 abs 函数的作用是返回一个给定数值的非负值(即该数值的绝对值)。 abs 函数接受一个参数&a…...

vue拼接html点击事件不生效
vue使用ts,拼接html,点击事件不生效或者报 is not defined 点击事件要用onclick 不是click let data{name:测,id:123} let conHtml <div> "名称:" data.name "<br>" <p class"cursor blue&quo…...

【Spring】Spring之依赖注入源码解析
1 Spring注入方式 1.1 手动注入 xml中定义Bean,程序员手动给某个属性赋值。 set方式注入 <bean name"userService" class"com.firechou.service.UserService"><property name"orderService" ref"orderService"…...

【微软知识】微软相关技术知识分享
微软技术领域 一、微软操作系统: 微软的操作系统主要是 Windows 系列,包括 Windows 10、Windows Server 等。了解 Windows 操作系统的基本使用、配置和故障排除是非常重要的。微软操作系统(Microsoft System)是美国微软开发的Wi…...

12.python设计模式【观察者模式】
内容:定义对象间的一种一对多的依赖关系,当一个对象的状态发生改变的时候,所有依赖于它的对象得到通知并被自动更新。观者者模式又称为“发布-订阅”模式。比如天气预报,气象局分发气象数据。 角色: 抽象主题…...
重生之我要学C++第五天
这篇文章主要内容是构造函数的初始化列表以及运算符重载在顺序表中的简单应用,运算符重载实现自定义类型的流插入流提取。希望对大家有所帮助,点赞收藏评论,支持一下吧! 目录 构造函数进阶理解 1.内置类型成员在参数列表中的定义 …...

复习之linux高级存储管理
一、lvm----逻辑卷管理 1.lvm定义 LVM是 Logical Volume Manager(逻辑卷管理)的简写,它是Linux环境下对磁盘分区进行管理的一种机制。 逻辑卷管理器(LogicalVolumeManager)本质上是一个虚拟设备驱动,是在内核中块设备和物理设备…...
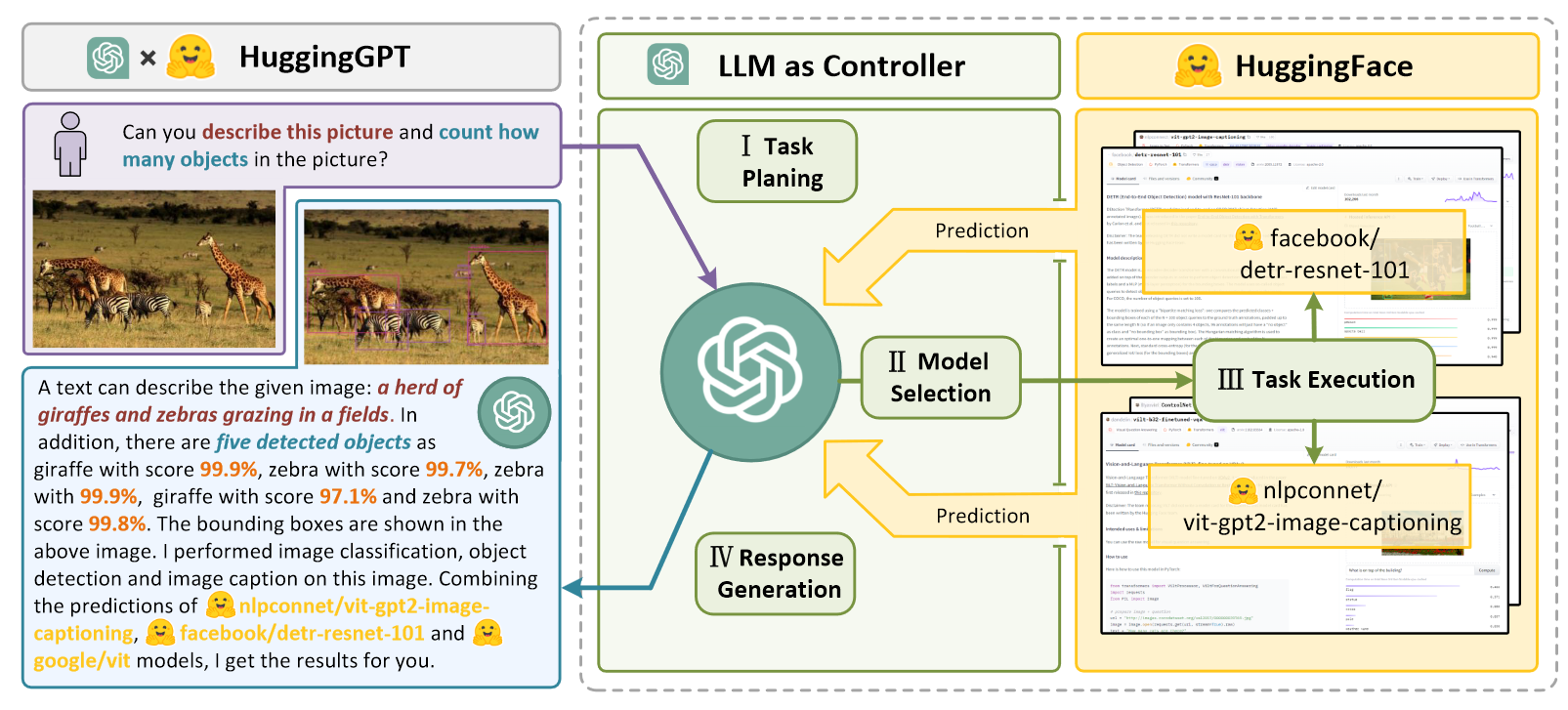
HuggingGPT Solving AI Tasks with ChatGPT and its Friends in Hugging Face
总述 HuggingGPT 让LLM发挥向路由器一样的作用,让LLM来选择调用那个专业的模型来执行任务。HuggingGPT搭建LLM和专业AI模型的桥梁。Language is a generic interface for LLMs to connect AI models 四个阶段 Task Planning: 将复杂的任务分解。但是这里…...

java工程重写jar包中class类覆盖问题
结论:直接在程序中复写jar中的类即可 原因:一般我java工程是运行在tomcat容器中,tomcat容易在加载我们工程类和jar包是的优先级为: 我们工程的class 先于 我们工程lib下的jar 重复的类只加载一次,加载我们复写后的类后…...

Mybatis基于注解与XML开发
文章目录 1 关于SpringBoot2 关于MyBatis2.1 MyBatis概述2.2 MyBatis核心思想2.3 MyBatis使用流程3 MyBatis配置SQL方式3.1 基于注解方式3.1.1 说明3.1.2 使用流程3.1.3 常用注解 3.2 基于XML方式3.2.1 相比注解优势3.2.2 使用流程3.2.3 常用标签 1 关于SpringBoot SpringBoot…...

数字化转型导师坚鹏:数字化时代扩大内需的8大具体建议
在日新月异的数字化时代、复杂多变的国际化环境下,扩大内需成为推动经济发展的国家战略,如何真正地扩大内需?结合本人15年的管理咨询经验及目前实际情况的深入研究,提出以下8大具体建议: 1、制定国民收入倍增计划。结…...
M1/M2 通过VM Fusion安装Win11 ARM,解决联网和文件传输
前言 最近新入了Macmini M2,但是以前的老电脑的虚拟机运行不起来了。😅,实际上用过K8S的时候,会发现部分镜像也跑不起来,X86的架构和ARM实际上还是有很多隐形兼容问题。所以只能重新安装ARM Win11,幸好微软…...

Linux中显示系统正在运行的进程的命令
2023年7月29日,周六上午 在Linux中,ps命令用于显示当前系统中正在运行的进程, ps应该是processes snapshot(进程快照)的缩写。 以下是ps命令的常见用法和示例: 显示当前用户的所有进程:ps 显示…...
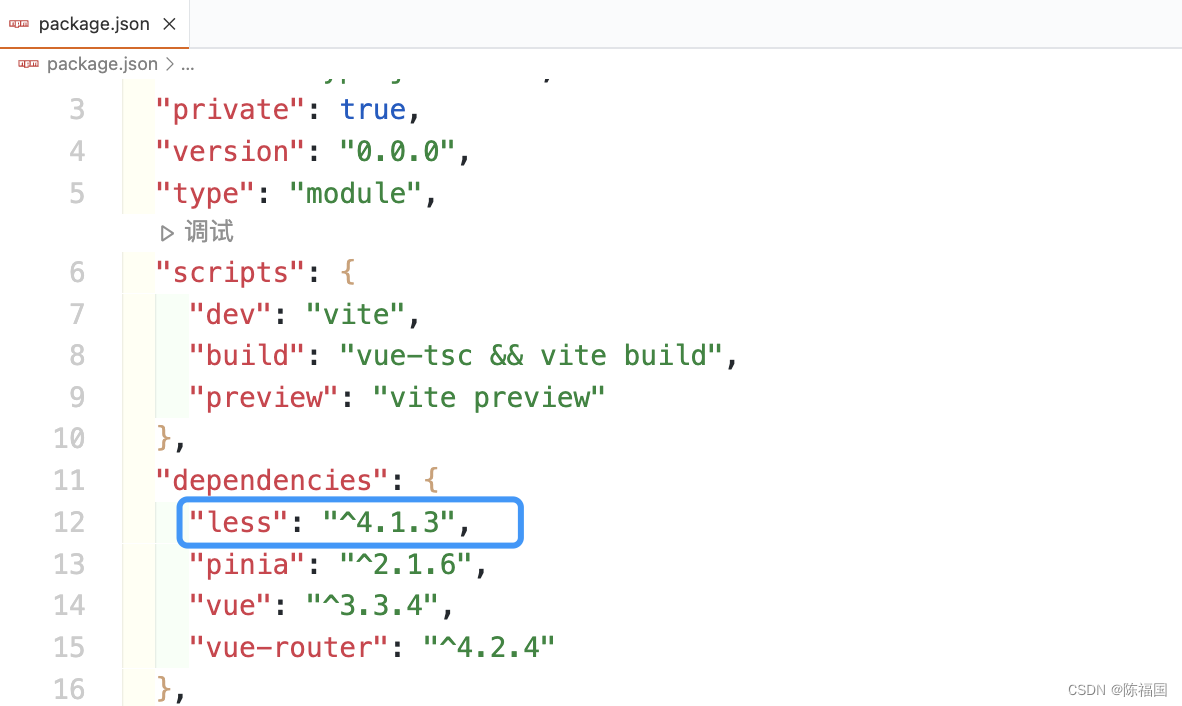
vite中安装less
使用vite创建的项目,默认是没有安装less的 如果直接在style中书写less 会报下图错误: 解决方案: npm install --save less 在package.json中查看是否安装成功 安装完成刷新页面,问题解决...
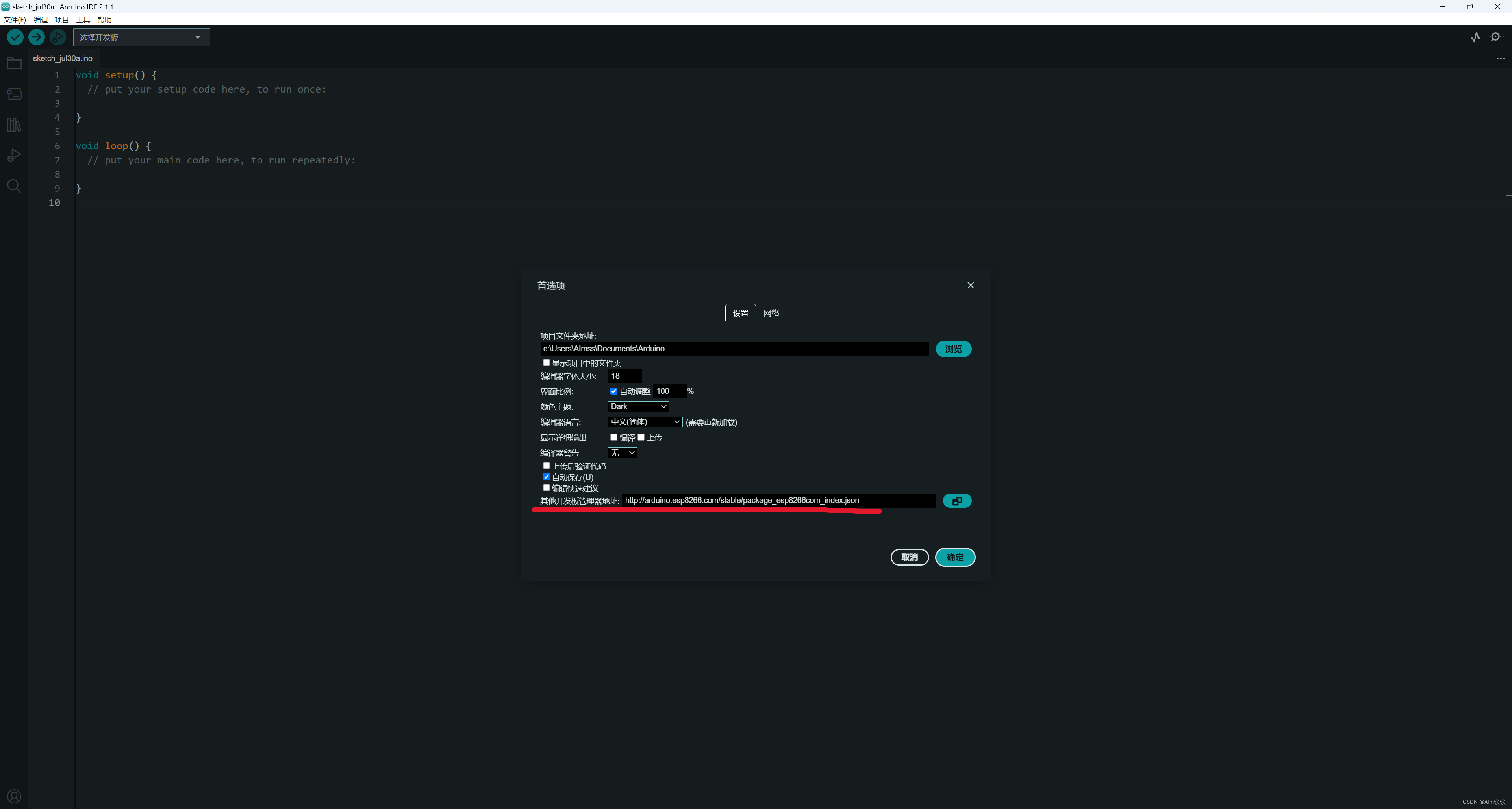
Aduino中eps环境搭建
这里只记录Arduino2.0以后版本:如果有外网环境,那么可以轻松搜到ESP32开发板环境并安装,如果没有,那就见下面操作: 进入首选项,将esp8266的国内镜像地址填入,然后保存,在开发板中查…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...
