现代C++中的从头开始深度学习:激活函数
一、说明
让我们通过在C++中实现激活函数来获得乐趣。人工神经网络是生物启发模型的一个例子。在人工神经网络中,称为神经元的处理单元被分组在计算层中,通常用于执行模式识别任务。
在这个模型中,我们通常更喜欢控制每一层的输出以服从一些约束。例如,我们可以将神经元的输出限制为 [0, 1]、[0, ∞] 或 [-1,+1] 的区间。另一个非常常见的场景是保证来自同一层的神经元总是相加 1。应用这些约束的方法是使用激活函数。
在这个故事中,我们将介绍 5 个重要的激活函数:sigmoid、tanh、ReLU、identity 和 Softmax。
二、关于本系列
在本系列中,我们将学习如何仅使用普通和现代C++对必须知道的深度学习算法进行编码,例如卷积、反向传播、激活函数、优化器、深度神经网络等。

这个故事是:C++中的激活函数
查看其他故事:
0 — 现代C++深度学习编程基础
1 — 在C++中编码 2D 卷积
2 — 使用 Lambda 的成本函数
3 — 实现梯度下降
...更多内容即将推出。
三、sigmoid激活
从历史上看,最著名的激活是Sigmoid函数:

Sigmoid 函数和一阶导数
此图表显示了 sigmoid 的三个重要属性:
- 其输出限制在 0 和 1 之间;
- 它是平滑的,或者用更好的数学术语来说,它是可微分的;
- 它是S形的。
你应该想知道为什么形状很重要?S 形模型意味着曲线类似于原点邻域中的线性曲线:

这有助于更快地收敛小输入。有两种方法可以定义 sigmoid 公式:

这两个公式是等效的,但在实现时,我们更愿意使用后者:
double sigmoid(double x)
{return 1. / (1. + exp(-x));
}我们更喜欢第二个公式的原因是第一个公式在数值上更不稳定。很多时候,我们在实现 sigmoid 时使用短路:
double sigmoid(double x)
{double result;if (x >= 45.) result = 1.;else if (x <= -45.) result = 0.;else result = 1. / (1. + exp(-x));return result;
}这节省了大量处理并避免了以下情况 |x|很大。
四、sigmoid导数
使用链式法则,我们可以找到 sigmoid 导数为:

为方便起见,我们将 sigmoid 及其一阶导数分组为一个函子:
class Sigmoid : public ActivationFunction
{public:virtual Matrix operator()(const Matrix &z) const{return z.unaryExpr(std::ref(Sigmoid::helper));}virtual Matrix jacobian(const Vector &z) const{Vector output = (*this)(z);Vector diagonal = output.unaryExpr([](double y) {return (1. - y) * y;});DiagonalMatrix result = diagonal.asDiagonal();return result;}private:static double helper(double z){double result;if (z >= 45.) result = 1.;else if (z <= -45.) result = 0.;else result = 1. / (1. + exp(-z));return result;}};我们将看到在介绍反向传播算法时如何使用激活函数导数。
Sigmoid 主要用于二元分类器或回归系统的输出层,其中结果始终为非负。如果输出可以是负值,请考虑使用下面描述的 Tanh 激活。
五、Tanh 激活
顾名思义,tanh 激活由双曲正切三角函数定义:
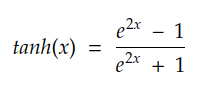
与 sigmoid 一样,tanh 也是 S 形且可微的。然而,tanh 的界限是 -1 和 1:

Tanh 函数和一阶导数
tanh 激活和 sigmoid 激活紧密相关:
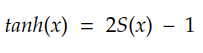
请注意,由于 tanh 可以输出负值,因此我们不能将其与 logcosh 等损失函数一起使用。
tanh 的一阶导数为:

我们可以将 tanh 及其导数打包到一个函子中:
class Tanh : public ActivationFunction
{public:virtual Matrix operator()(const Matrix &z) const{return z.unaryExpr(std::ref(tanh));}virtual Matrix jacobian(const Vector &z) const{Vector output = (*this)(z);Vector diagonal = output.unaryExpr([](double y) {return (1. - y * y);});DiagonalMatrix result = diagonal.asDiagonal();return result;}
};六、RELU
Sigmoid 和 Tanh 的一个问题是它们的计算成本非常高,使得训练时间更长。ReLU是一个简单的激活:

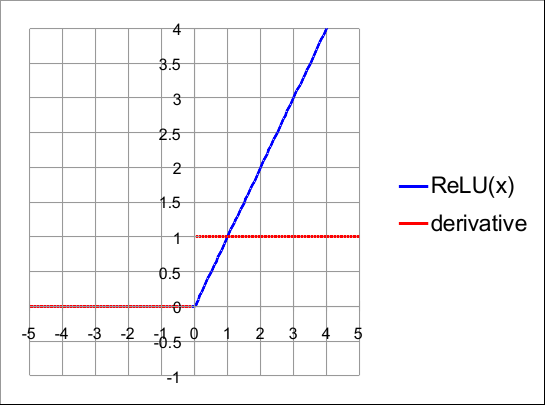
ReLU活化和一阶导数
由于ReLU是一个简单的比较,因此与其他函数相比,其计算成本非常低。
我们可以按如下方式实现 ReLU:
class ReLU : public ActivationFunction
{public:virtual Matrix operator()(const Matrix &z) const{return z.unaryExpr([](double v) {return std::max(0., v);});}virtual Matrix jacobian(const Vector &z) const{Vector output = (*this)(z);Vector diagonal = output.unaryExpr([](double y) {double result = 0.;if (y > 0) result = 1.; return result;});DiagonalMatrix result = diagonal.asDiagonal();return result;}};相关要点是:
- 它对负值有界,但对正 x 值未绑定:[0, ∞]
- 当 x = 0 时,它是不可微分的。在实践中,我们通过假设当 x = 0 时导数 dRelu(x)/dx 为 0 来放宽此条件。
由于 ReLU 基本上由单个比较组成,因此我们谈论的是一个非常快速的计算操作。它的第一阶导数也可以快速计算:
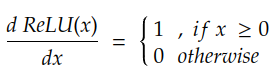
尽管有其优点,但ReLu有三个主要缺点:
- 由于它不是正有界的,我们不能使用它来控制输出到 [0, 1]。正因为如此,在实践中,ReLU通常只存在于内部(隐藏)层中。
- 由于 ReLu 对于任何 x < 0 都是 0,有时我们的模型在训练过程中只是“死亡”,因为部分或所有神经元都停留在仅输出 0 的状态。
- 由于 ReLU 的导数在 x = 0 时不连续,因此对于某些输入,模型的训练可能不稳定。
有一些替代方法可以解决这些问题(参见Softplus,leakyReLU,ELU和GeLU)。然而,由于相当大的好处,ReLU仍然广泛用于现实世界的模型。
七、身份激活
身份激活的定义很简单:

其导数为:

使用身份激活意味着神经元的输出不会以任何方式被修改。在这种情况下,实现非常简单:
class Identity : public ActivationFunction
{public:virtual Matrix operator()(const Matrix &z) const { return z; }virtual Matrix jacobian(const Vector &z) const{Vector diagonal = Vector::Ones(z.rows());DiagonalMatrix result = diagonal.asDiagonal();return result;}
};
恒等式和一阶导数
八、softmax
考虑到我们有一张宠物的照片,我们需要确定它是哪种动物:狗?一只猫?仓鼠?一只鸟?豚鼠?在机器学习中,我们通常将此类问题建模为分类问题,并将模型称为分类器。
Softmax非常适合作为分类器的输出,因为它实际上表示离散概率分布。例如,请考虑以下示例:

猫、狗和鸟的分类器
在前面的示例中,网络非常确定图像中的宠物是猫。在下一个示例中,模型将图像评分为狗:

在深度学习模型中,我们使用 Softmax 来表示这种类型的输出。
这张惊人的宠物照片是由Amber Janssens拍摄的
8.1 定义SoftMax
Softmax的原始公式是:

这个公式意味着,如果我们有 k 个神经元,第 i 个神经元的输出由 x i 的指数除以每个神经元 xj 的指数之和给出。
Softmax的第一个实现可以是:
const auto buggy_softmax(const Vector &z) {Vector expo = z.array().exp();Vector sums = expo.colwise().sum();Vector result = expo.array().rowwise() / sums.transpose().array();return result;};我们很快就会看到这种实现存在严重缺陷。但是这段代码的工作是说明softmax最重要的方面:每个神经元的结果取决于每个单独的输入。
我们可以运行以下代码:
Vector input1 = Vector::Zero(3);
input1 << 0.1, 1., -2.;std::cout << "Input 1:\n" << input1.transpose() << "\n\n";
std::cout << "results in:\n" << buggy_softmax(input1).transpose() << "\n\n";到输出:

Softmax最重要的两个方面是:
- 所有神经元的总和始终为 1
- 每个神经元值在区间 [0, 1] 内
8.2 实现SoftMax
我们之前的 softmax 实现的问题在于指数函数增长非常快。例如,e¹⁰ 大约是 22,026,但 e¹⁰⁰ 是 2.688117142×10 ⁴³,这是一个令人生畏的巨大数字。事实证明,即使我们使用适度的数字作为输入,我们的实现也会失败:
Vector input2 = Vector::Zero(4);
input2 << 100, 1000., -500., 200.;std::cout << "Input 2:\n" << input2.transpose() << "\n\n";
std::cout << "results in:\n" << buggy_softmax(input2).transpose() << "\n\n";
std::cout << "using the buggy implementation.\n";
发生这种情况是因为C++浮点具有固定的表示形式。使用常规 64 位处理器,任何通过 750 或更多字符的调用都会导致数字。cmath exp(x)inf
幸运的是,我们可以使用以下技巧来修复它:

其中 m 是最大输入:
![]()
现在,通过修复代码,我们得到:
const auto good_softmax(const Vector &z) {Vector maxs = z.colwise().maxCoeff();Vector reduc = z.rowwise() - maxs.transpose();Vector expo = reduc.array().exp();Vector sums = expo.colwise().sum();Vector result = expo.array().rowwise() / sums.transpose().array();return result;};
溢出是数值不稳定的一个来源。
当我们开发现实世界的深度学习系统时,数值稳定性是一个非常普遍的问题。
8.3 Softmax衍生产品
Softmax和其他激活之间存在非常明显的差异。通常,像sigmoid或ReLU这样的激活是系数操作,即一个系数的值不会影响其他系数。当然,在 Softmax 中,这不是真的,因为所有值都需要求和 1。这种依赖性使得softmax导数的计算有点棘手。尽管如此,经过一点点的计算并使用我们的老朋友链规则,我们可以弄清楚:

如果您想阅读此衍生品的发展,请告诉我。
例如,如果我们有 5 个神经元,则每个神经元相对于同一层中每个神经元的导数由下式给出:
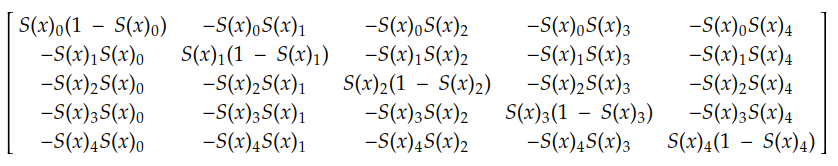
这个导数将在下一个故事中应用,当我们训练第一个分类器时。
九、包装SoftMax以供进一步使用
最后,我们可以按如下方式实现 Softmax 函子:
class Softmax : public ActivationFunction
{public:virtual Matrix operator()(const Matrix &z) const{if (z.rows() == 1){throw std::invalid_argument("Softmax is not suitable for single value outputs. Use sigmoid/tanh instead.");}Vector maxs = z.colwise().maxCoeff();Matrix reduc = z.rowwise() - maxs.transpose();Matrix expo = reduc.array().exp();Vector sums = expo.colwise().sum();Matrix result = expo.array().rowwise() / sums.transpose().array();return result;}virtual Matrix jacobian(const Vector &z) const{Matrix output = (*this)(z);Matrix outputAsDiagonal = output.asDiagonal();Matrix result = outputAsDiagonal - (output * output.transpose());return result;}};如今,几乎每个分类器都在输出层中使用 Softmax。我们将在接下来的故事中介绍softmax的一些真实示例。
十、其他激活函数
还有其他几个激活函数。除了这里描述的那些,我们还可以列出Softplus,Softsign,SeLU,Elu,GeLU,指数,swish等。一般来说,它们是sigmoid或ReLU的一些变体。
十一、结论和下一步
激活函数是机器学习模型最重要的构建块之一。在这个故事中,我们学习了一些最重要的:Sigmoid,Tanh,ReLU,Identity和Softmax。
在下一个故事中,我们将深入探讨最重要的深度学习算法的实现:反向传播。从零开始,在C++和本征。
相关文章:
现代C++中的从头开始深度学习:激活函数
一、说明 让我们通过在C中实现激活函数来获得乐趣。人工神经网络是生物启发模型的一个例子。在人工神经网络中,称为神经元的处理单元被分组在计算层中,通常用于执行模式识别任务。 在这个模型中,我们通常更喜欢控制每一层的输出以服从一些约束…...

python怎么实现tcp和udp连接
目录 什么是tcp连接 什么是udp连接 python怎么实现tcp和udp连接 什么是tcp连接 TCP(Transmission Control Protocol)连接是一种网络连接,它提供了可靠的、面向连接的数据传输服务。 在TCP连接中,通信的两端(客户端和…...
)
java设计模式-观察者模式(jdk内置)
上一篇我们学习了 观察者模式。 观察者和被观察者接口都是我们自己定义的,整个设计模式我们从无到有都是自己设计的,其实,java已经内置了这个设计模式,我们只需要定义实现类即可。 下面我们不多说明,直接示例代码&am…...

秒级体验本地调试远程 k8s 中的服务
点击上方蓝色字体,选择“设为星标” 回复”云原生“获取基础架构实践 背景 在这个以k8s为云os的时代,程序员在日常的开发过程中,肯定会遇到各种问题,比如:本地开发完,需要部署到远程k8s集群,本地…...

CV前沿方向:Visual Prompting 视觉提示工程下的范式
prompt在视觉领域,也越来越重要,在图像生成,作为一种可控条件,增进交互和可控性,在多模态理解方面,指令prompt也使得任务灵活通用。视觉提示工程,已然成为CV一个前沿方向! 下面来看看…...

Redis五大基础类型解析
1.String类型 特征:即存储字符串的类型,单个字符串存储量最大不超过512MB 常用业务场景:⽤来存储JSON序列化之后对象 底层编码: int编码 数据结构特点:ptr指针直接指向字符串常量池中对应字符串地址,而…...
)
在CSDN学Golang云原生(服务网格istio)
一,在Kubernetes上部署istio 在Kubernetes上部署istio,可以按照以下步骤进行: 安装Istio 使用以下命令从Istio官网下载最新版本的Istio: curl -L https://istio.io/downloadIstio | ISTIO_VERSION<VERSION> sh - 其中&…...

Golang 获取本地 IP 地址方法
在 Golang 中,使用 net 包可以很方便地获取到本机IP地址。 借助 net.InterfaceAddrs 方法 简单示例代码如下: package mainimport ("fmt""net" )func main() {addrList, err : net.InterfaceAddrs()if err ! nil {panic(err)}for…...

抖音seo短视频账号矩阵系统技术开发简述
说明:本开发文档适用于抖音seo源码开发,抖音矩阵系统开发,短视频seo源码开发,短视频矩阵系统源码开发 一、 抖音seo短视频矩阵系统开发包括 抖音seo短视频账号矩阵系统的技术开发主要包括以下几个方面: 1.前端界面设…...
运维高级--shell脚本完成分库分表
为什么要进行分库分表 随着系统的运行,存储的数据量会越来越大,系统的访问的压力也会随之增大,如果一个库中的表数据超过了一定的数量,比如说MySQL中的表数据达到千万级别,就需要考虑进行分库分表; 其…...
)
Mysql 忘记密码怎么重置密码(详细步骤)
每种方法都有其适用的情况,根据具体情况选择合适的方法。无论选择哪种方法,请务必在重置密码后及时删除临时用户并重新启动 MySQL 服务。 一、使用 mysqladmin 重置密码 停止服务 # systemctl 启动的使用这个停止 $ sudo systemctl stop mysql# mac 本机…...

机器学习深度学习——图像分类数据集
👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er 🌌上期文章:机器学习&&深度学习——softmax回归(下) 📚订阅专栏:机器学习&&深度学习…...

【PWN · 栈迁移】[BUUCTF]ciscn_2019_es_2
第一道栈迁移题目,跌跌撞撞理解了 前言 当前溢出可用空间比较少时(极端情况下仅能覆写ebp和ret),可以通过栈迁移的方式,扩大shellcode的容纳空间,其核心是将esp移动到一段shellocode开头。而esp总是由ebp赋…...
: 网络通信常用命令(后续待补充))
网络编程(13): 网络通信常用命令(后续待补充)
ifconfig 一般用于查看网卡信息 ping 一般用于侦测本机到目标网络主机的网络是否通常: ping ip/域名 telnet 可以用于指定ip地址和端口的侦听服务是否存在:telnet ip port, 也可以模拟客户端给服务器发数据 netstat 用于查看网络连接状态 -a: 显示所有选项 -t&#…...

flask创建数据库连接池
flask创建数据库连接池 在Python中,您可以使用 Flask-SQLAlchemy 这个扩展来创建一个数据库连接池。Flask-SQLAlchemy 是一个用于 Flask 框架的 SQLAlchemy 操作封装,实现了 ORM(Object Relational Mapper)。ORM 主要用于将类与数据库中的表建立映射关系…...
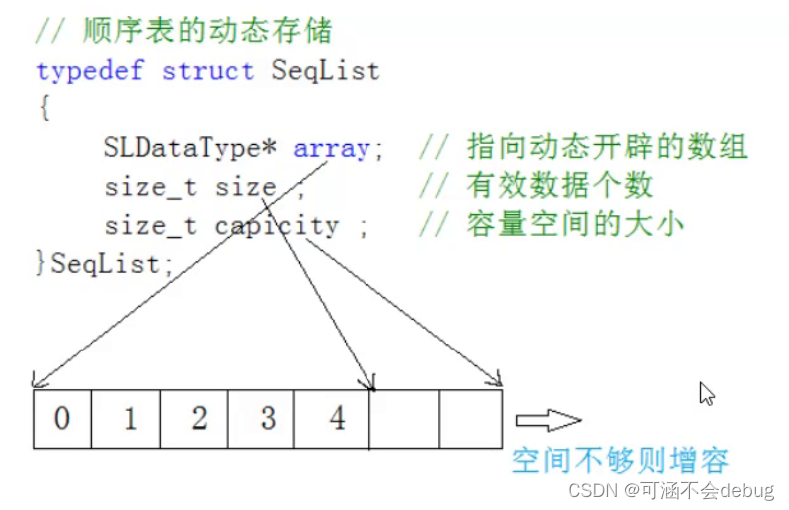
C语言手撕顺序表
目录 一、概念 1、静态顺序表:使用定长数组存储元素。 2、动态顺序表:使用动态开辟的数组存储 二、接口实现 1、对顺序表的初始化 2、对数据的销毁 3、对数据的打印 4、检查是否需要扩容 5、尾插 6、头插 7、尾删 8、头删 9、在pos位置插入x …...

常见的排序算法
常见的排序算法 常见的排序算法包括: 冒泡排序(Bubble Sort):依次比较相邻的元素,将较大的元素交换到右侧,逐步将最大元素移动到末尾。插入排序(Insertion Sort):将数组…...
C#如何使用SQLite数据库?
文章目录 0.引言1.SQLite工具准备2.创建窗体项目并添加SQLite的命名空间3.编写使用SQLite代码4.结果展示 0.引言 SQLite是一个轻量级的嵌入式数据库,它的库文件非常小巧,不需要独立的服务器进程或配置。这使得它非常适合在资源受限的环境中使用ÿ…...

如何将表格中的状态数据转换为Tag标签显示
考虑到系统前端页面的美观程度,通常通过Tag标签来代替某条数据中的状态信息。仅通过一点操作,便能够使得页面美观程度得到较大提升,前后对比如下所示。代码基于Vue以及Element-ui组件实现。 修改前: 修改后: 修改前…...
centos中修改防火墙端口开放配置
1、直接进入文件修改 vim /etc/sysconfig/iptables 2、添加需要开放的端口 (1)添加需要开放的单个端口 4001 -A INPUT -m state --state NEW -m tcp -p tcp --dport 4001 -j ACCEPT (2)添加需要开放的某个网段端口 4001:4020 …...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...
