Sort_Algorithm
排序算法
- 前言
- 插入排序
- 折半插入排序
- 希尔排序
- 冒泡排序
- 快速排序
- 选择排序
- 堆排序
- 归并排序
前言
排序算法:将一堆数据元素按关键字递增或者递减的顺序,进行排序。
排序算法的评价指标:时间复杂度,空间复杂度,算法稳定性。
算法稳定性: 关键字相同的元素在排序之后相对位置不变。
内部排序:数据都在内存中,数据量不大,能放在内存中(关注时、空复杂度)
外部排序:数据量太大,无法放入全部内存,数据放在在磁盘中(关注磁盘读写次数)
插入排序
算法思想:每次将一个待排序的元素按其关键字大小插入到前面已经排好的子序列中,知道其全部记录插入完成。
void Insert_sort1(int* a,int n)
{for (int i = 1; i < n; i++){if (a[i] < a[i - 1]){//后小于前int j = i - 1;//标记前int temp = a[i];//保存后while (j >= 0 && a[j]>temp)/*后移,腾位,不能写成a[j]<a[i],因为第一次移位(i=j+1)后,a[i]就被覆盖了,并不是原先的值,这也是为什么要保存a[i]的值的原因*/{a[j+1] = a[j];--j;}//当a[j]<temp时循环跳出,此时腾出了j+1这个位置a[j+1] = temp;}}
}
对于排序算法,要明确知道所定义的每一个变量的含义,以及在循环过程中的变化情况,死记硬背是万不可行,要掌握核心思想,仔细体会在细节的处理。
折半插入排序
在前面已有序序列中查找,待插入元素位置,因为前面已经是有序序列所以可用折半查找,折半查找效率O(logn)。
void Binary_insert_sort(int* a, int n)
{int i, j, low, high, mid;for (i = 1; i < n; i++){int temp = a[i];low = 0; high = i - 1;while (low<=high){mid = (low + high) / 2;if (a[mid]>temp)high = mid - 1;else low = mid + 1;}for (int j = i - 1; j >= high + 1; --j)a[j + 1] = a[j];a[high + 1] = temp;}
}
分析优化情况,实际上这样优化只是减少了之前在while循环中的比较次数,总体时间复杂度还是O(n^2),因为依然要移动大量元素。想到这里,能不能在链表中用折半插入排序呢?答案是:不可以!
原因在于折半查找,利用了数组能够通过小标随机访问的特性,而链表无法做到随机访问,只能从前往后遍历,所以无法应用折半查找,但可以利用插入排序。
希尔排序
对待排序表,按一定增量进行分割成子表,对每个子表进行直接插入排序,增量d=d/2。
不断缩小增量,最后d=1时为直接插入排序,因为前面的每次排序致使元素已经基本有序,而直接插入排序,当元素基本有序时,时间复杂度较低,这也就是希尔排序时间复杂度降低的原因。
/*
算法思想:缩小增量的直接插入排序,利用直接插入排序在元素基本有序时,时间复杂度接近O(n),来降低时间复杂度
每次对小规模的子表进行排序,最后一次的子表已经是表本身
理解希尔排序代码,首先要充分理解直接插入排序的思想
*/
int shell_sort(int* a, int n)
{int num = 0;for (int d = n / 2; d >= 1; d /= 2)//增量设置,每次÷2,终值为1,直接插入排序{for (int i = d; i < n; i++)//对i不可以进每次加d操作,对i的遍历,已经从0开始变为d开始{int j = i - d;//原先是减一,现在为减dint temp = a[i];if (a[i]<a[i - d]){num++;for (j = i - d; j >= 0 && a[j] > temp; j -= d)//循环每次减da[j + d] = a[j];a[j + d] = temp;//参照插入排序,1变d}}}return 1;
}
不稳定排序,只能用于线性表,不能用于链表。
冒泡排序
从后往前或从前往后两两比较相邻元素的值,若为逆序,则交换,直到序列比较完。
每一趟排序,是最小的元素冒到最前。每一趟确定一个元素的位置。
稳定排序,适用于链表
#include<stdbool.h>
void swap(int* a, int j)
{int temp = a[j];a[j] = a[j - 1];a[j - 1] = temp;
}int Bubble_sort(int* a, int n)
{for (int i = 0; i < n-1; i++){bool flag = false;for (int j = n -1; j >i; j--)//j>i,i前的元素已经有序,从后往前冒泡,前面元素有序{if (a[j - 1] > a[j])//左大于右才交换,稳定{swap(a,j);flag = true;//标记一趟循环是否进行过交换}}if (flag == false)//没有进行交换,说明表中元素已有序,提前退出return 1;}return 1;
}
注意两个for循环的n-1,对i的n-1是最后一个元素不判断
对j的n-1是从最后一个元素开始判断是否逆序,逆序则交换,直到j<=i
快速排序
分治思想,每次选一位置元素作为枢轴,进行数组划分,划分结果要让枢轴之前都<=,枢轴之后都>,这样也就确定了一个枢轴元素的位置,并接着以此枢轴划分为两个子数组,对子数组再进行划分,最终将所有元素排好序。
int Partition(int*, int, int);
void Quick_sort(int* a,int low,int high)
{if (low < high)//递归跳出{int pivotpos = Partition(a, low, high);//划分Quick_sort(a, low, pivotpos - 1);//枢轴以左Quick_sort(a, pivotpos + 1, high);//枢轴以右}
}
int Partition(int* a, int low, int high)//时间复杂度O(n),对表用low,high指针扫描一遍
{int pivot = a[low];while (low < high)//low,high指针相遇时跳出,共同所指位置即枢轴元素应放位置,此时前都比其小,后都比其大{while (low < high&&a[high] >= pivot) --high;//当出现小于枢轴时跳出while,此时high所指就是小于枢轴a[low] = a[high];//low最初的值已经保存在pivot中,可视为low此时空出,直接放入,每次while只能交换一个值while (low < high&&a[low] <= pivot) ++low;//low指针右移找到比枢轴大的跳出while,low此时所指为大于枢轴的元素,下步移动a[high] = a[low];//在上面high的值已经被存入,所以视high为空,放入low值}//跳出最外层while,此时low=high,所指相同,且其原值已经被保存到别处,可视为空,则放入pivota[high] = pivot;//a[high]=pivot;是一样的return high;//return high;是一样的
}
/*
快排时间复杂度O(n*递归层数)
如果每次选择的枢轴元素都刚好是顺序的中间元素的值,则递归层数为logn
最好时间复杂度O(nlogn)
最坏O(n^2)
*/
跑一亿随机数排序时会崩。
int Partition(int*, int, int);
void Quick_sort(int* a,int low,int high)
{if (low < high){int pivotpos = Partition(a, low, high);Quick_sort(a, low, pivotpos - 1);Quick_sort(a, pivotpos + 1, high);}
}
int Partition(int* a, int low, int high)
{int pivot = a[low];while (low < high){while (low < high&&a[high] >= pivot) --high;a[low] = a[high];while (low < high&&a[low] <= pivot) ++low;a[high] = a[low];}a[high] = pivot;return high;
}
选择排序
每次选取未排序列的最小值,与当前未排序的第一个位置交换,知道最后一个元素。
void Choice_sort(int* a, int n)
{for (int i = 0; i < n-1; i++){int min=i;for (int j = i+1; j < n; j++)//在二层for循环外无判断,所以内层for始终都要被执行{if (a[j] < a[min])min = j;//min保存最小值下标,用小标处理相对于用值处理要简单}//找到最小a[j],与a[i]交换if (min!=i)//若当前a[i]就是未排序中最小,则不用交换{int temp = a[i];a[i] = a[min];a[min] = temp;}}
}
/*
不稳定,也使用于链表
无论待排序列是否有序,时间复杂度都是 n(n-1)/2 -> O(n^2)
*/
堆排序
/*
大根堆,小根堆(完全二叉树)逻辑视角,因为是完全二叉树,可以用数组存(存储视角)
根>=左右孩子
根<=左右孩子
i的左孩子 2i
i的右孩子 2i+1
i的父节点 i/2(向下取整)
构建和维护大根堆
检查非终端节点 i<=(n/2),是否满足大根堆的要求
*/
void HeadAdjust(int*, int, int);
void BuildMaxHeap(int* a, int len)
{for (int i = len / 2; i > 0; i--)//从后往前遍历非终端结点HeadAdjust(a, i, len);
}
//将以k为根的子树调整为大根堆(局部微调)
void HeadAdjust(int* a, int k, int len)
{int root = a[k];//暂存子树的根节点,注意是子树for (int i = 2 * k; i <= len; i *= 2)//i=2*k,所以此时i表达k的左孩子{if (i < len&&a[i] < a[i + 1])//取左右孩子的较大值i++;if (root >= a[i])break;//根大于较大值,说明该子树满足大根堆,退出else //否则交换二者{a[k] = a[i];k = i;//进行交换,则改变了其他子树的大根堆,所以要更新k值,继续向下检查}}a[k] = root;
}
void Heap_Sort(int* a, int len)
{BuildMaxHeap(a, len);for (int i = len; i >= 0; i--){int temp = a[i];a[i] = a[0];a[0] = temp;//大根堆,所以和堆顶元素交换HeadAdjust(a, 0, i - 1);//交换后,堆顶元素到了叶子结点不必再考虑它,修正大根堆}
}
构建大根堆,每次选择堆顶元素,已选元素与叶子交换,就不再看,维护其他结点构成大根堆,大根堆逐渐缩小,最后只剩一个根结点时,其实已经变成小根堆。
不稳定排序
时间复杂度O(nlogn)
归并排序
把两个或多个已经有序的序列合并成一个
所以分为“2路”归并和多路归并
m路归并,每次选出一个关键字需对比m-1次。
内部排序中一般采用2路归并
//递归实现
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<stdbool.h>
int* b;
void meger(int* a, int l, int mid, int r)
{// int* b=(int*)malloc(sizeof(int)*n);//辅助数组b不能在这里申请,应定义为全局,首先定义全局指针,然后再main函数中申请空间 int k = l;int i, j;for (i = l, j = mid + 1; i <= mid&&j <= r;k++)//不能在for中进行i,j的增{if (a[i]>a[j])b[k] = a[j++];else b[k] = a[i++];}//循环结束条件就是i,j之一越界其子数组,只是其中一个下标越界while (i<=mid)b[k++] = a[i++];while (j<=r)b[k++] = a[j++];for (int i = l; i <= r; i++)//处理好的b赋给aa[i] = b[i];
}
void megersort(int* a, int l, int r)
{if (l >= r) return;int mid = (l + r) / 2;megersort(a, l, mid);megersort(a, mid + 1, r);meger(a, l, mid, r);
}
void pint(int* a, int n)
{for (int i = 0; i<n; i++)printf("%d ", a[i]);
}
int main()
{clock_t s, f;srand(time(0));int n;scanf("%d", &n);b = (int*)malloc(4 * n);int* a = (int*)malloc(4 * n);for (int i = 0; i<n; i++)a[i] = rand() % 100 + 1;//pint(a, n);s = clock();megersort(a, 0, n - 1);f = clock();printf("time=%f\n", (float)(f - s)/1000);printf("\n");//pint(a, n);return 0;
}
递归结束:当划分的数组只有一个元素时,开始合并,并且只有一个元素的子数组必然是有序的
归并的过程就像形成一颗二叉树,二叉树有logn层,归并排序要logn趟,每趟都要O(n)时间,就像当于遍历一遍,时间复杂度为O(nlogn)
空间复杂度O(n),主要是要用到一个和原数组大小相同辅助数组,还有递归栈但是栈只要logn,低阶舍去。
稳定排序。
相关文章:

Sort_Algorithm
排序算法前言插入排序折半插入排序希尔排序冒泡排序快速排序选择排序堆排序归并排序前言 排序算法:将一堆数据元素按关键字递增或者递减的顺序,进行排序。 排序算法的评价指标:时间复杂度,空间复杂度,算法稳定性。 算…...
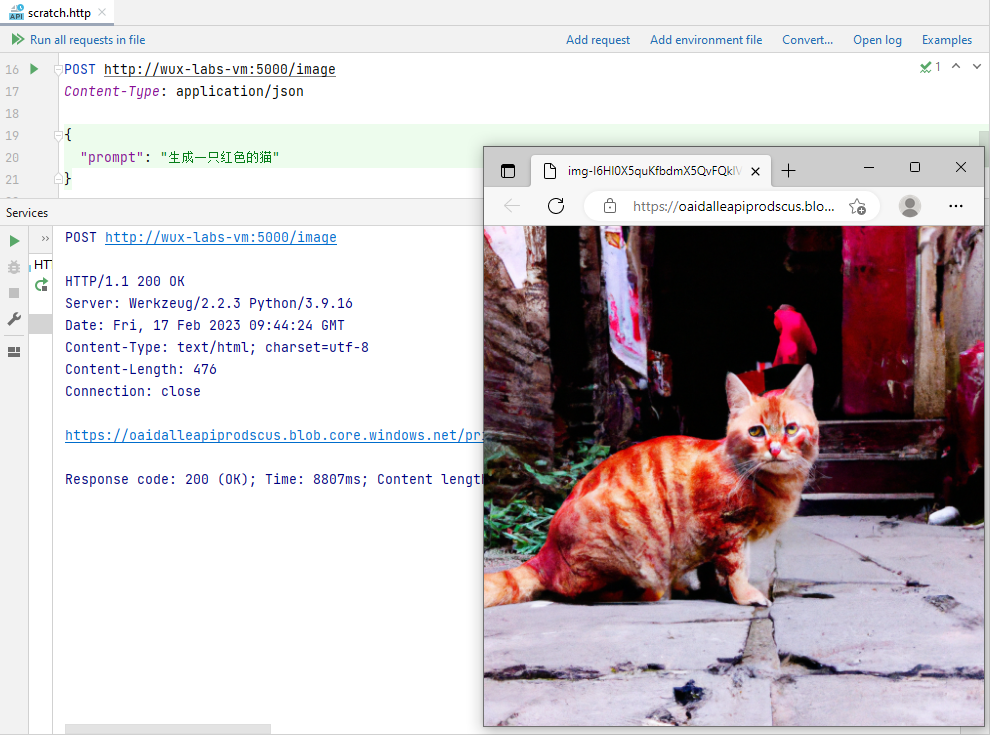
【初探人工智能】2、雏形开始长成
【初探人工智能】2、雏形开始长成【初探人工智能】2、雏形开始长成安装Flask封装Web接口雏形设置接收参数功能验证聊天写代码代码补全生成图片写在后面笔者初次接触人工智能领域,文章中错误的地方还望各位大佬指正! 【初探人工智能】2、雏形开始长成 在…...
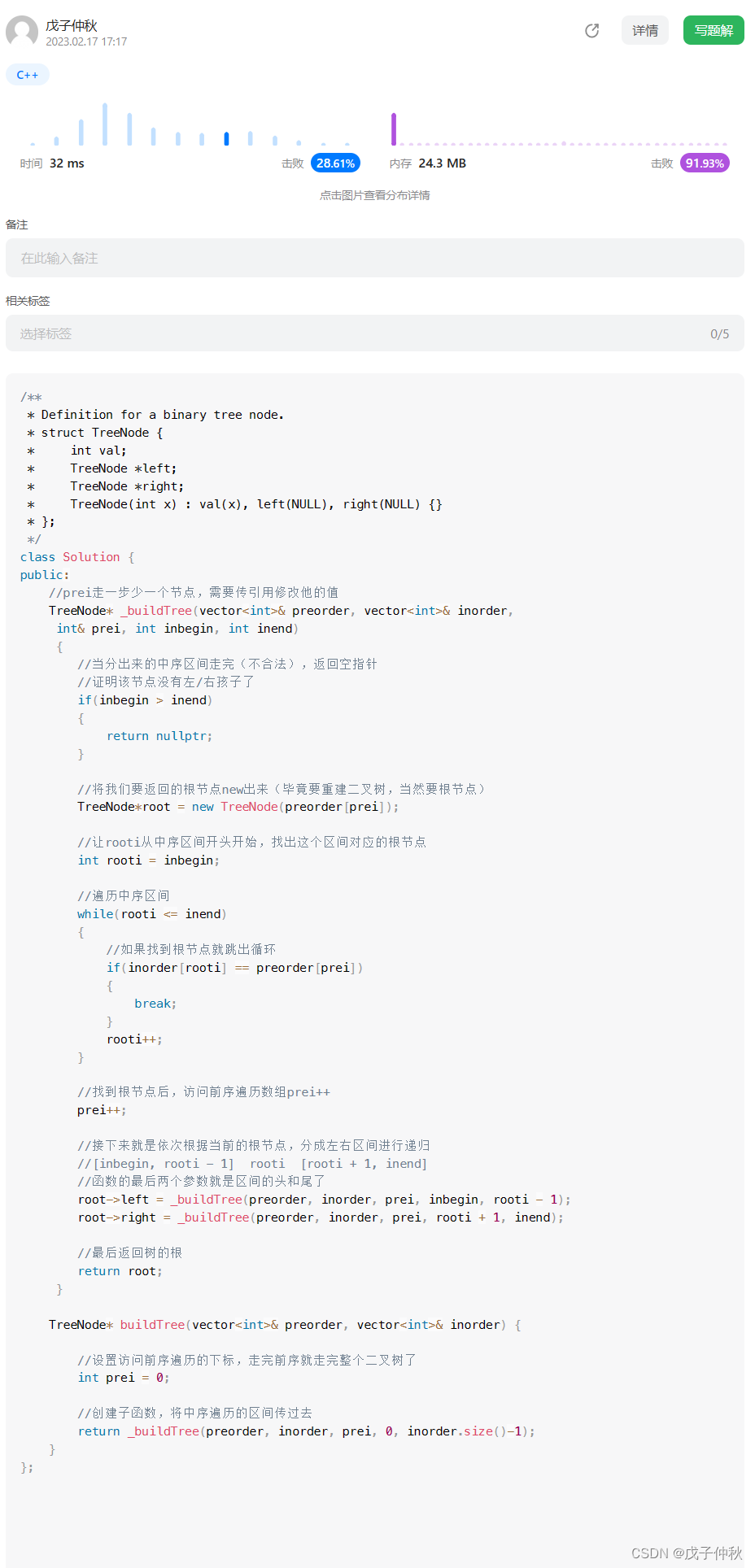
【LeetCode】剑指 Offer(2)
目录 写在前面: 题目: 题目的接口: 解题思路: 代码: 过啦!!! 写在最后: 写在前面: 今天的每日一题好难,我不会dp啊啊啊啊啊啊。 所以&am…...

【JavaSE】Lambda、Stream(659~686)
659.每天一考 1.写出获取Class实例的三种常见方式 Class clazz1 String.class; Class clazz2 person.getClass(); //sout(person); //xxx.yyy.zzz.Person... Class clazz3 Class.forName(String classPath);//体现反射的动态性2.谈谈你对Class类的理解 Class实例对应着加载…...
求梯度和Hessian Matrix(海森矩阵)的python实现)
有限差法(Finite Difference)求梯度和Hessian Matrix(海森矩阵)的python实现
数学参考 有限差方法求导,Finite Difference Approximations of Derivatives,是数值计算中常用的求导方法。数学上也比较简单易用。本文主要针对的是向量值函数,也就是f(x):Rn→Rf(x):\mathbb{R^n}\rightarrow \mathbb{R}f(x):Rn→R当然&…...

day33 贪心算法 | 1005、K次取反后最大化的数组和 134、加油站 135、分发糖果
题目 1005、K次取反后最大化的数组和 给定一个整数数组 A,我们只能用以下方法修改该数组:我们选择某个索引 i 并将 A[i] 替换为 -A[i],然后总共重复这个过程 K 次。(我们可以多次选择同一个索引 i。) 以这种方式修改…...

《蓝桥杯每日一题》递推·AcWing 3777. 砖块
1.题目描述n 个砖块排成一排,从左到右编号依次为 1∼n。每个砖块要么是黑色的,要么是白色的。现在你可以进行以下操作若干次(可以是 0 次):选择两个相邻的砖块,反转它们的颜色。(黑变白…...
)
mysql读写分离(maxscale)
1. 环境架构 需要三台服务器。192.168.2.10(master)192.168.2.20(slave)192.168.2.30(maxscale) 2. 部署mysql主从同步 mysql主从同步可以参考mysql主从同步 3. 部署maxscale服务 MaxScale中间件软件 …...
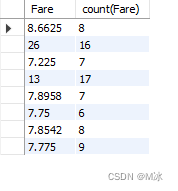
第八章 - 数据分组( group by , having , select语句顺序)
第八章 - 数据分组 group by数据分组过滤分组 having分组排序groub by语句的一些规定select语句顺序数据分组 在使用group by进行分组时,一般都会配合聚合函数一起使用,实现统计数据的功能。比如下面例子,需要按性别计算人数。按性别进行分组…...

Git(GitHub,Gitee 码云,GitLab)详细讲解
目录第一章 Git 概述1.1 何为版本控制1.2 为什么需要版本控制1.3 版本控制工具1.4 Git 简史1.5 Git 工作机制1.6 Git 和代码托管中心第二章 Git 安装第三章 Git 常用命令3.1 设置用户签名3.2 初始化本地库3.3 查看本地库状态3.3.1 首次查看(工作区没有任何文件&…...
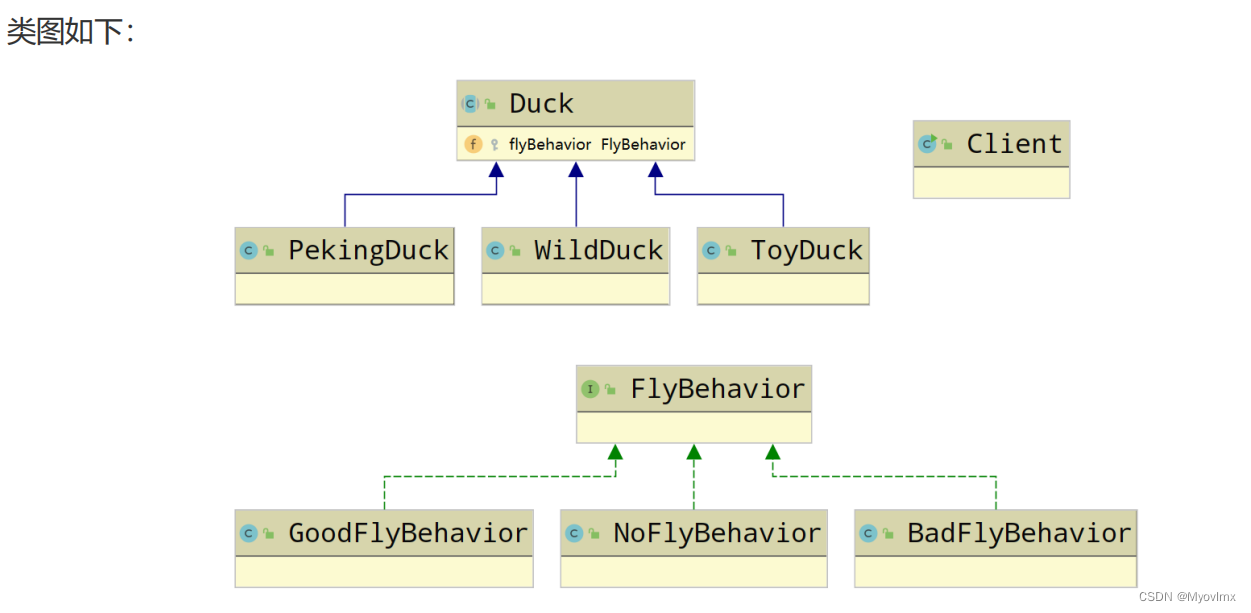
策略模式(Strategy Pattern)
编写鸭子项目,具体要求如下: 1) 有各种鸭子(比如 野鸭、北京鸭,水鸭等,鸭子有各种行为,比如 叫,飞行等) 2)显示鸭子的信息 传统方案解决鸭子问题 1࿰…...
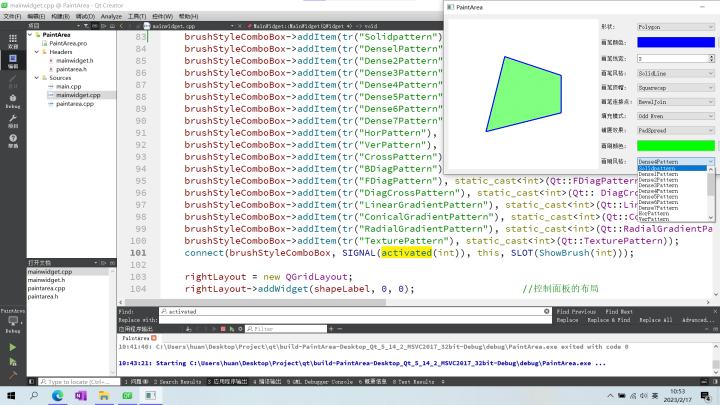
《Qt6开发及实例》6-2 Qt6基础图形的绘制
目录 一、绘图框架设计 二、绘图区的实现 2.1 PaintArea类 2.2 PaintArea类讲解 三、主窗口的实现 3.1 MainWidget类 3.2 MainWidget类讲解 3.3 槽函数编写 3.5 其他内容 一、绘图框架设计 界面 两个类 二、绘图区的实现 2.1 PaintArea类 paintarea.h #ifndef…...

LeetCode 382. 链表随机节点
原题链接 难度:middle\color{orange}{middle}middle 题目描述 给你一个单链表,随机选择链表的一个节点,并返回相应的节点值。每个节点 被选中的概率一样 。 实现 SolutionSolutionSolution 类: Solution(ListNodehead)Solution…...
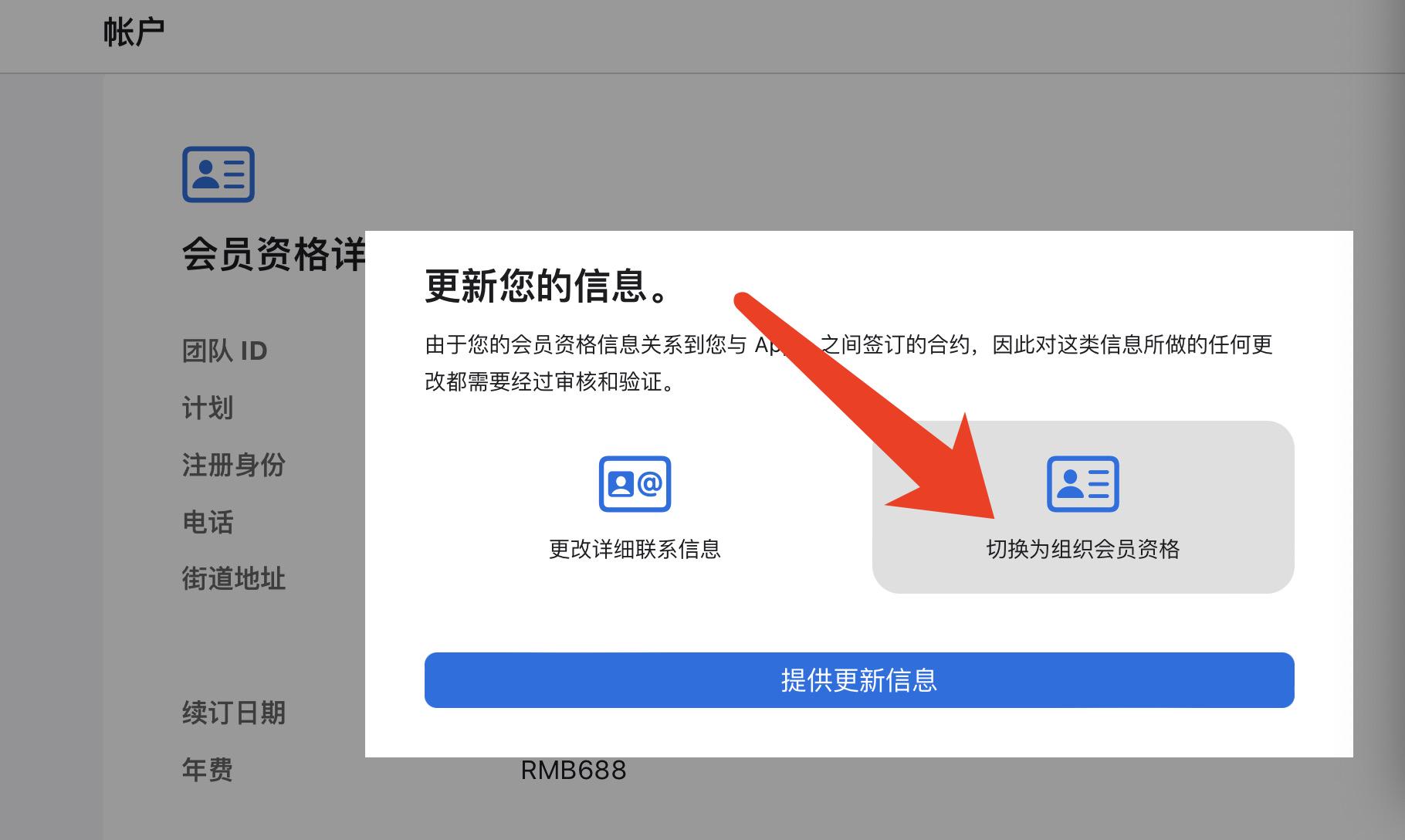
iOS开发AppleDeveloper中给别人授权开发者权限后,对方一直显示不了我的开发账号team
在iOS开发经常出现多人协作开发的情况。这时我们通常要发邮件邀请别的用户为开发者或者app管理就可以开发我们自己的项目了。但是这次我给别人授权开发者权限后,发现别人权限中没有证书相关权限如图:并且别人登录该账号后,在xcode中只有一个看…...

FreeRTOS数据类型和编程规范
目录 数据类型 变量名 函数名 宏的名 数据类型 每个移植的版本都含有自己的portmacro.h头文件,里面定义了2个数据类型 TickType_t FreeRTOS配置了一个周期性的时钟中断:Tick Interrupt每发生一次中断,中断次数累加,这被称为t…...
【python知识】win10下如何用python将网页转成pdf文件
一、说明 本篇记录一个自己享用的简单工具。在大量阅读网上文章中,常常遇到一个专题对应多篇文章,用浏览器的收藏根本不够。能否见到一篇文章具有搜藏价值,就转到线下,以备日后慢慢消化吸收。这里终于找到一个办法,将在…...
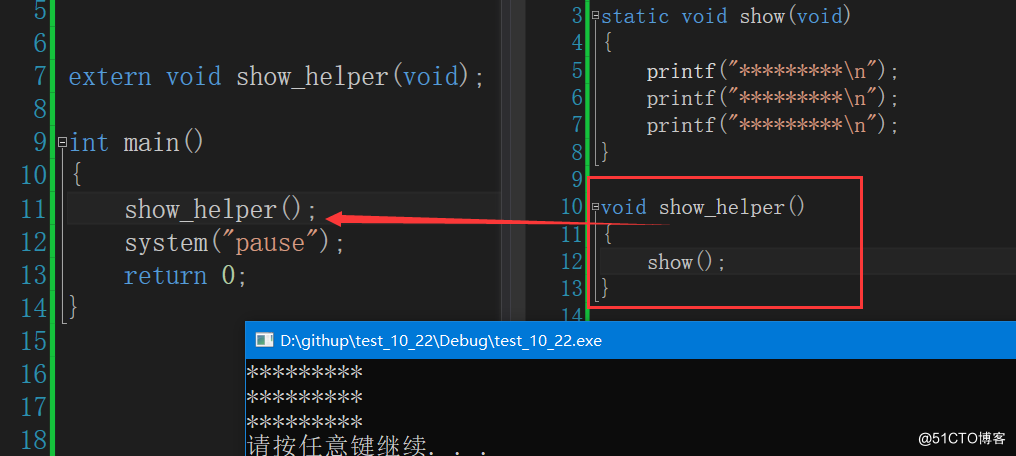
C语言常见关键字
写在前面 这个博客是结合C语言深度解剖这本书和我以前学的知识综合而成的,我希望可以更见详细的谈一下C语言的关键字,内容有点多,有错误还请斧正. 常见关键字 下面我们说下C语言的关键字,所谓的关键字是指具有特定功能的单词,我们可以使用关键字来帮助我们完成不同的事物.C语…...

【MT7628】固件开发-SDK4320添加MT7612E WiFi驱动操作说明
解压5G WiFi MT7612E驱动1.1解压指令 tar -xvf MT76x2E_MT7620_LinuxAP_V3.0.4.0_P2_DPA_20160308.tar.bz2 1.2解压之后会出现以下两个目录 rlt_wifi rlt_wifi_ap 1.3将解压后的文件拷贝到系统下 拷贝路径 RT288x_SDK/source/linux-2.6.36.x/drivers/net/wireless 内核中打开驱…...
如何从手工测试进阶自动化测试?阿里10年测开经验分享...
随着行业的竞争加剧,互联网产品迭代速度越来越快,QA 与测试工程师都需要在越来越短的测试周期内充分保证质量。可是,App 测试面临着很多挑战,比如多端发布、多版本发布、多机型发布等等,导致了手工测试很难完全胜任。因…...
C++复习笔记11
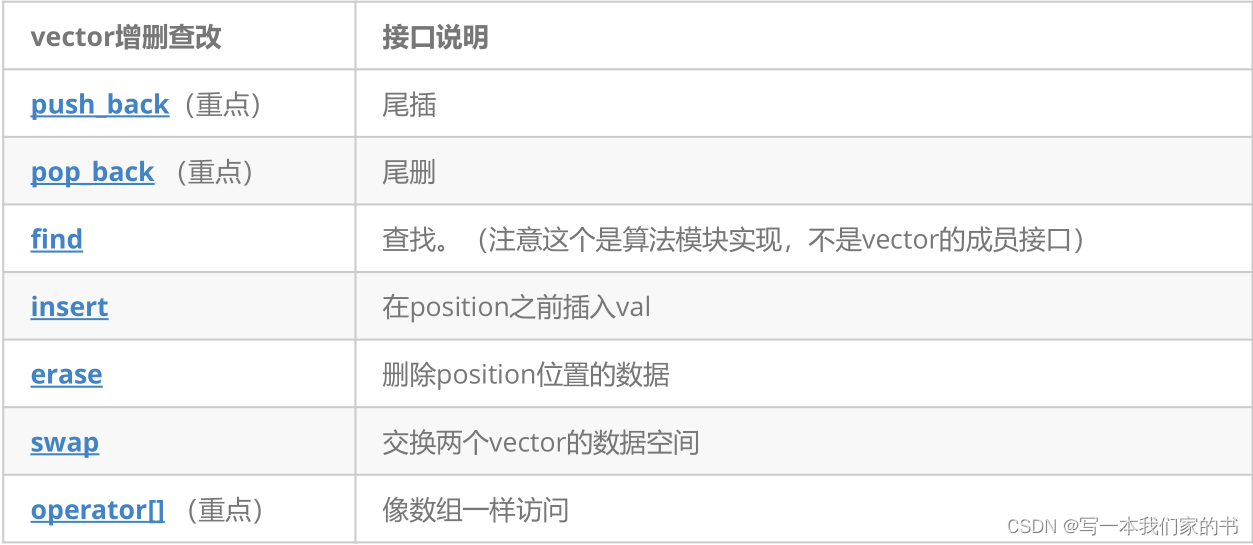
1. vector是表示可变大小数组的序列容器。 2. 就像数组一样,vector也采用的连续存储空间来存储元素。也就是意味着可以采用下标对vector的元素进行访问,和数组一样高效。但是又不像数组,它的大小是可以动态改变的,而且它的大小会被…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...
