【Java基础】泛型(二)-泛型的难点:通配符
本文将尝试将通配符和泛型中的继承,多态一并讲解
关于泛型中继承的注意事项
因为Integer、Double继承了Number,根据多态性,以下语句是合法的
Number n = new Integer(10); // OK, 父类引用变量可以指向子类对象
n = 2.9 // OK,n实际上会指向一个新的Double对象
但是注意,像ArrayList()、ArrayList()和ArrayList没有任何继承关系,考虑以下这个例子:
List<Integer> li = new ArrayList<Integer>();
List<Number> ln = li; // illegal,这一句不合法
ln.add(new Float(3.1415)); //这一句本来是合法,因为Float继承了Number。
对象ln是List类型,ln.add(new Float(3.1415))其实是合法的
但是如果你允许List类型的引用指向List,那么ln就是li的一个别名,这个List理论上就是个Integer列表,不能放Float类型对象了,这就产生了矛盾
而多态本身就是在运行时确定对象真正的类型,所以编译时发现不了ln.add(new Float(3.1415))其实已经不合法了
索性,编译时就不允许List ln = li
需要注意,以下这种泛型类是有继承关系的
//不替换
public class ArrayList<E> extends AbstractList<E>implements List<E> { //ArrayList后面必须添加<E>boolean add(E e);E get(int index);
}//替换
public class StringArrayList extends ArrayList<String> { boolean add(String e); //方法重写String get(int index);
}
这时,以下的继承关系都是正确的:
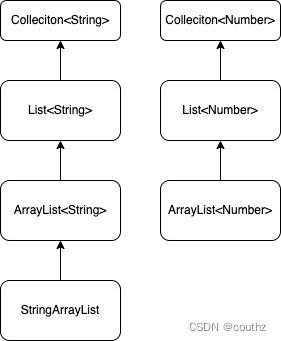
通配符类型
通配符介绍
上节说了半天,像ArrayList和ArrayList两者完全没有继承关系,其实就是为了引出通配符
因为这时泛型似乎不能利用多态的优点了,比如我就想在我的工具类里编写一个针对各种Number类型List的求和方法,我总不能对每种Number类型都写一个重载方法,这其实又违背了多态的理念
public Number sum(List<Number> list) {//求和
}
这种情况就可以用到通配符:?
例如这个求和方法就可以写成:
public Number sum(List<? extends Number> list) {//求和//get
}
这里的语义是:sum方法的入参可以是任何Number类型的List。(实际上,List<Integer>,List <Double>都属于List<? extends Number>的子类,因此多态性就可以体现出来了,这里的继承关系后面会进行总结)
(需要注意的是,这时的sum方法其实已经不属于泛型方法了,“?”和类型参数“T”相比,不属于一个类型的形参,它其实和Integer、Number一样都属于实际类型,只不过它是“不确定类型”)
深入理解通配符
各种类型的通配符及继承关系
这一小节尝试将通配符和继承关系一并讲解:
其实,理解通配符的一个要点就是:通配符就是在泛型中实现多态的一种方式
通配符的种类有三种:
- 限定上界的通配符 List<? extends Number>
- 限定下界的通配符 List<? super Integer>
- 无界通配符 List<?>
同时,这些带通配符的类型,有以下的继承关系:
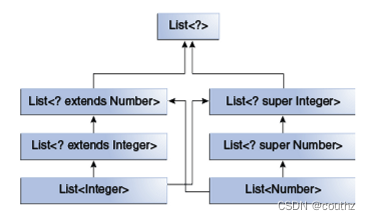
限定上界的通配符:上一节中我们已经编写了一个针对各种Number类型List的求和方法,利用的就是限定上界的通配符,因为List<Integer>,List<Double>等各种Number类型List都是List<? extends Number>的子类,所以我们将List<? extends Number>作为形参,很好地利用了多态性
限定下界的通配符:而限定下界的通配符,是希望未知类型“?”是某种特定类型的超类,比如说工具类中有一个方法是向list中添加Integer类型变量,那么这个list的类型可以是List, List, 或List,因为它们都可以存Integer类型,这时就可以用到限定下界的通配符
public static void addNumbers(List<? super Integer> list) {for (int i = 1; i <= 10; i++) {list.add(i);}
}
从继承关系上看,这时的参数可以是List,当然也可以是List
无界通配符:其实List<?>就是List<? extends Object>,对比之前限定上界的例子,我们使用List<? extends Number>来声明求和方法,也是因为Number变量可以直接用+进行相加,但一般的Object变量没有相加的能力。换句话说,如果我们用List<?>来编写方法,我们仅会用到内部对象作为Object时的能力。
比如,编写一个方法让任何对象的list都能够逐一输出:
public static void printList(List<?> list) {for (Object elem: list)System.out.print(elem + " ");
}
另一种场景是,我们编写的方法用到了泛型类,但是调用的都是该泛型类中不依赖于类型参数的方法。
例如Collections中的shuffle方法,用于打乱list的顺序,其实它的逻辑就是将list中元素逐一和任意元素进行交换,因此需要遍历,调用list.size(), 而这个方法并不关心list<E>中的类型参数到底是啥
public static void shuffle(List<?> list, Random rnd)
各种类型通配符的使用指导
这里主要翻译官方教程的使用指导:
- 如果你使用的泛型类对象,是一个“in”变量,即为代码提供数据,就应该使用extends关键字
- 如果你使用的泛型类对象,是一个“Out”变量,即保存代码中的数据,就应该使用super关键字
- 如果仅会用到Object类定义的方法来访问“in”变量,就使用无界通配符
- 如果对象既是in或者out变量,就不要使用通配符
- 以上这些使用指导不适用于通配符出现在返回值的情况
Collections的copy方法其实就证实了前两点
public static <T> void copy(List<? super T> dest, List<? extends T> src)
这里个人的理解是:限定输入类型的上界,输出类型的下界,这样数据从输入到输出会是向上转型,会是安全的。
另外,官方教程中也提到,一旦参数的类型是List<? extends …>,最好就让它只读,因为根据继承关系可能有以下问题
//自然数类
class NaturalNumber {private int i;public NaturalNumber(int i) { this.i = i; }// ...
}//偶数类
class EvenNumber extends NaturalNumber {public EvenNumber(int i) { super(i); }// ...
}List<EvenNumber> le = new ArrayList<>();
List<? extends NaturalNumber> ln = le;
ln.add(new NaturalNumber(35)); // 异常
相关文章:

【Java基础】泛型(二)-泛型的难点:通配符
本文将尝试将通配符和泛型中的继承,多态一并讲解 关于泛型中继承的注意事项 因为Integer、Double继承了Number,根据多态性,以下语句是合法的 Number n new Integer(10); // OK, 父类引用变量可以指向子类对象 n 2.9 // OK,n实…...

黑马】后台管理-两个括号的坑
记录一下这两天的坑没想到后台管理系统上线这两天都没有搞明白1.首先第一个坑是使用node.js的express中间件框架创建一个微型服务器,然后将vue脚手架生成的dist文件夹的文件放入里面了 ,把项目加载到web服务器之后运行node .\app.js,页面显示…...

05:进阶篇 - 使用 CTKWidgets
作者: 一去、二三里 个人微信号: iwaleon 微信公众号: 高效程序员 CTKWidgets 包含了一组 Qt 部件,用于生物医学成像应用程序。当然,即使你的程序与医学无关,很多部件也是很有参考意义的。 在 CTK 源码中,有很多选项开关,可以控制你想要编译的内容(详见:04:进阶篇 …...
【YOLO V5】代码复现过程
接上篇,讲到如何从mask转成YOLOv5训练需要的txt数据集格式,这篇就在此基础上进行模型训练预测和部署转换吧! 目录 1.环境准备 2.YOLO训练 2.1 数据集准备 2.2 data.yaml准备 2.3 yolov5.yaml准备 2.4 训练命令 3.YOLO预测 3.1OLOv5 P…...
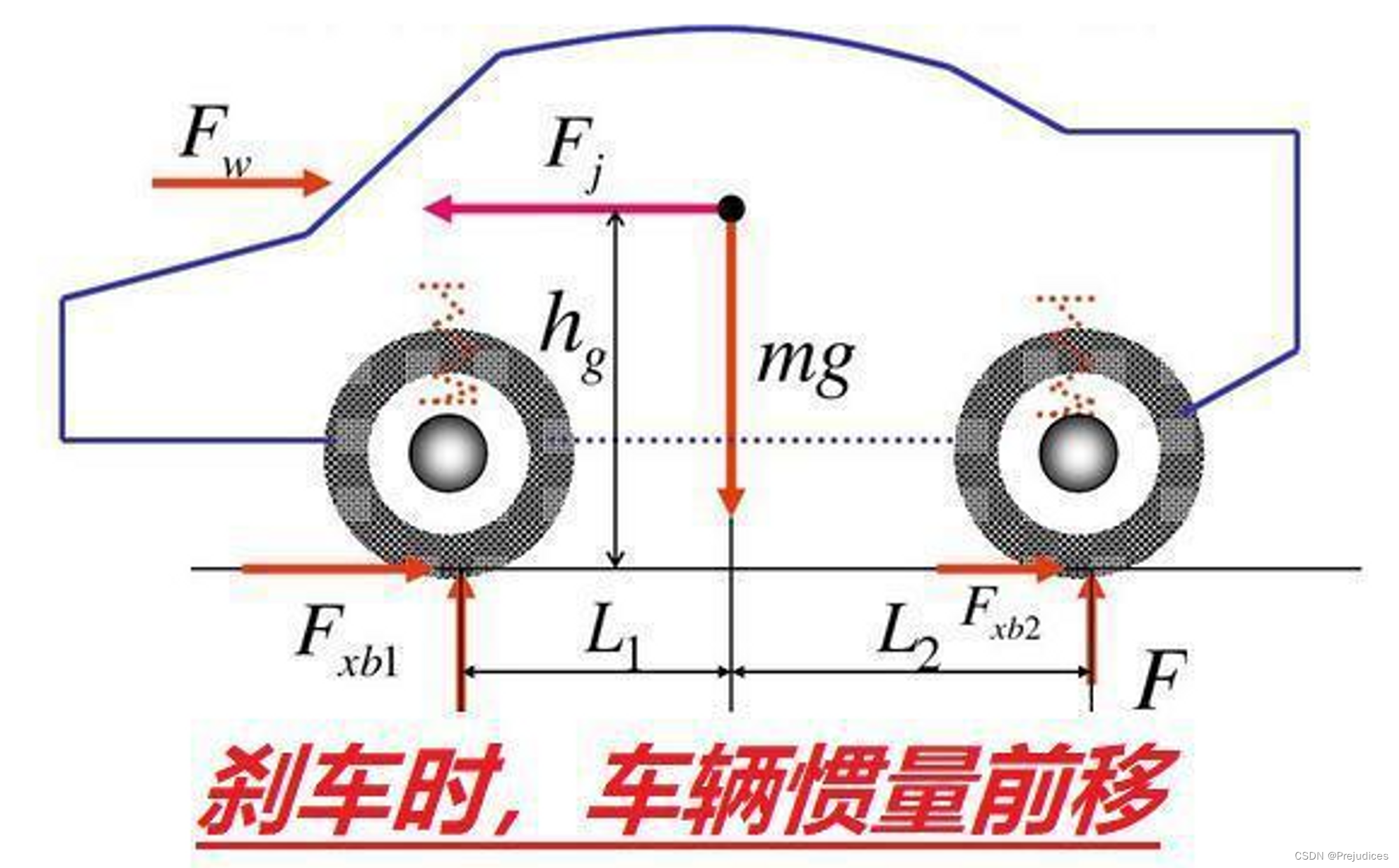
汽车如何实现制动
汽车如何实现制动 汽车如何实现制动 难点答疑:汽车刹车时,四个车轮是如何制动的?制动机理是什么? 第一步:驾驶员踩下制动踏板,推动制动主缸 第二步:制动主缸将制动液的压力通过制动管道传递到四…...

cmake 引入第三方库(头文件目录、库目录、库文件)
程序的编写需要用到头文件,程序的编译需要lib文件,程序的运行需要dll文件,因此cmake引入第三方库其实就是将include目录、lib目录、bin目录引入工程。 目录 1、find_package(批量引入库文件和头文件) 2、include_dir…...
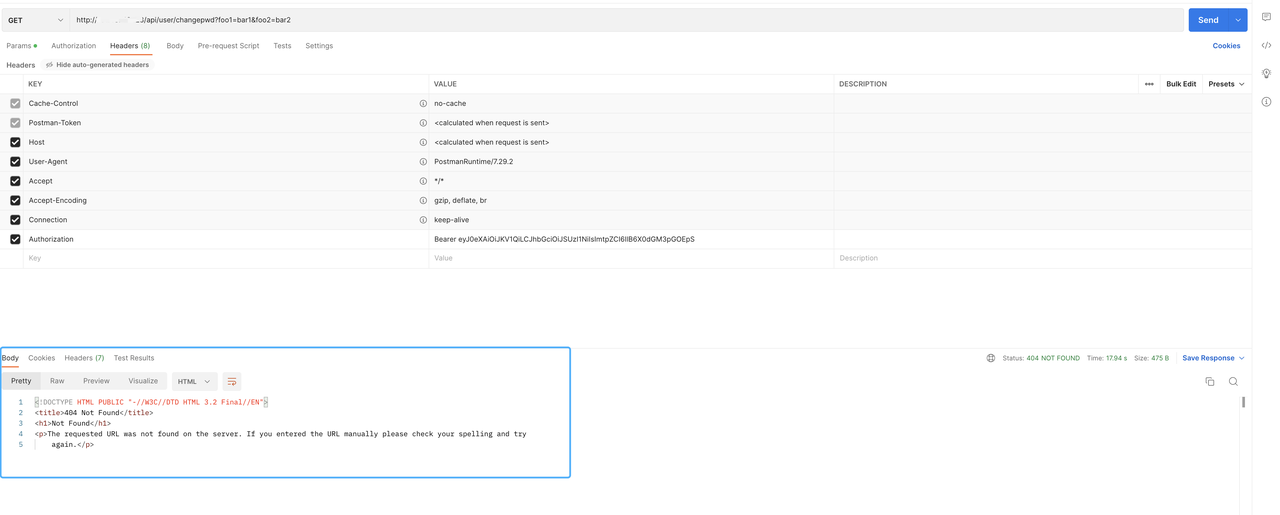
插件开发版|Authing 结合 APISIX 实现统一可配置 API 权限网关
当开发者在构建网站、移动设备或物联网应用程序时,API 网关作为微服务架构中不可或缺的控制组件,是流量的核心进出口。通过有效的权限管控,可以实现认证授权、监控分析等功能,提高 API 的安全性、可用性、拓展性以及优化 API 性能…...

deepinlinux v20安装rust和tauri并配置vscode开发工具过程
rust 很快进入linux内核开发,作为高效后台语言值得学习 tauri是代替electron的跨平台框架,不打包浏览器内核,所以打包出来体积小 安装rust 命令 curl --proto https --tlsv1.2 -sSf https://sh.rustup.rs | sh 安装后看版本 rustc -V 看构…...

通俗易懂的机器学习——sklearn鸢尾花分类(KNN)
前言 KNN算法是机器学习中较为简单的入门算法,其主要思想是选取k个与待预测点相近的数据,观察他们的类别,本着离谁近就更像谁的思路对于待预测点进行预测,本文将针对使用sklearn进行KNN算法的使用进行详解 数据预处理 在正式开…...
操作系统引论
操作系统是管理硬件和软件的一种应用程序。操作系统是运行在计算机上最重要的一种软件,它管理计算机的资源和进程以及所有的硬件和软件。它为计算机硬件和软件提供了一种中间层,使应用软件和硬件进行分离,让我们无需关注硬件的实现࿰…...
 经验贴汇总)
优质 CS 读博 (PhD) 经验贴汇总
前言 如果你对这篇文章可感兴趣,可以点击「【访客必读 - 指引页】一文囊括主页内所有高质量博客」,查看完整博客分类与对应链接。 Advice for early-stage Ph.D. students 读博的核心是在研究上取得进展,只有在研究上取得一些进展ÿ…...

SpringCloud学习笔记 - @SentinelResource的fallbackblockHandler配置详解 - sentinel
1. sentinel服务负载均衡测试 sentinel默认开启了负载均衡的轮询模式,为了测试sentinel服务负载均衡的效果,需要先创建两个服务提供者和一个服务消费者。 1.1. 分别创建两个服务提供者-支付服务9003、9004 1. 添加pom依赖: 提供者只需要将…...
)
华为OD机试题 - 静态扫描最优成本(JavaScript)
最近更新的博客 2023新华为OD机试题 - 斗地主(JavaScript)2023新华为OD机试题 - 箱子之形摆放(JavaScript)2023新华为OD机试题 - 考古学家(JavaScript)2023新华为OD机试题 - 相同数字的积木游戏 1(JavaScript)2023新华为OD机试题 - 最多等和不相交连续子序列(JavaScri…...

mysql大数据量批量提交
DROP PROCEDURE IF EXISTS test.insert_bacth_commit_test1;CREATE PROCEDURE test.insert_bacth_commit_test1()begindeclare start_num int default 0; -- 初始设置起始行数declare end_num int default 5;-- 初始设施结束行数declare cnt_srouce int default 0; -- 定义源表…...

IP SAN组网配置
目录一、确认网络连接畅通二、服务器端ISCSI启动器配置1.以root身份登录2.验证是否已安装iSCSI启动器3.安装iSCSI启动器4.启动iSCSI服务5.给iSCSI启动器命名6.扫描目标器7.登录目标器8.将登录目标器行为设置为自启动三、主机多路径配置四、存储配置五、主机挂载背景:…...

面试7分看能力,3分靠嘴皮,剩下90分就靠这份Java面试八股文
有句话说的好,面试中7分靠能力,3分靠嘴皮刚开始面试的时候,介绍项目一般都是凸显我们技能的重中之重,它对一次面试的成败可以说具有决定性作用,这就涉及到我们的表达能力了,有人说我其实水平都在线…...

api接口如何对接?
对于很多产品小白或求职者而言,API接口是一个产品和研发领域的专业术语,大家可能在文章或者PRD中都已经有接触过API接口的概念。 实际上,接口的应用已经非常广泛和成熟,这个概念主要活跃在公司内部的各系统之间的衔接和对接以及公…...

毕业2年不到选择跳槽,居然拿到25K的薪资,简直了···
本人本科就读于某普通院校,毕业后通过同学的原因加入软件测试这个行业,角色也从测试小白到了目前的资深工程师,从功能测试转变为测试开发,并顺利拿下了某二线城市互联网企业的Offer,年薪 30W 。 选择和努力哪个重要&am…...
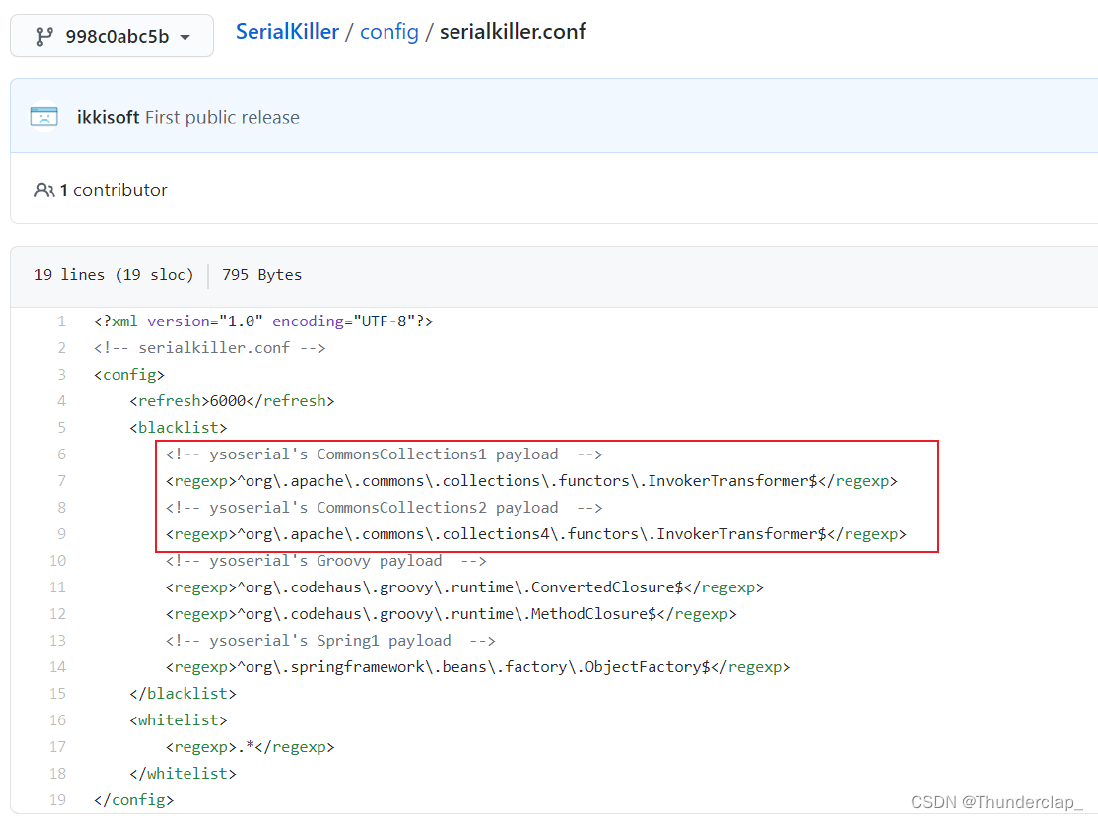
Java反序列化漏洞——CommonsCollections3链分析
一、原理CC1链中我们是通过调用Runtime.getRuntime.exec()来执行系统命令,而另一个方向我们可以通过TemplatesImpl加载字节码的类,通过调⽤其newTransformer() 方法,即可执⾏这段字节码的类构造器,我们在类构造器中加入恶意代码&a…...
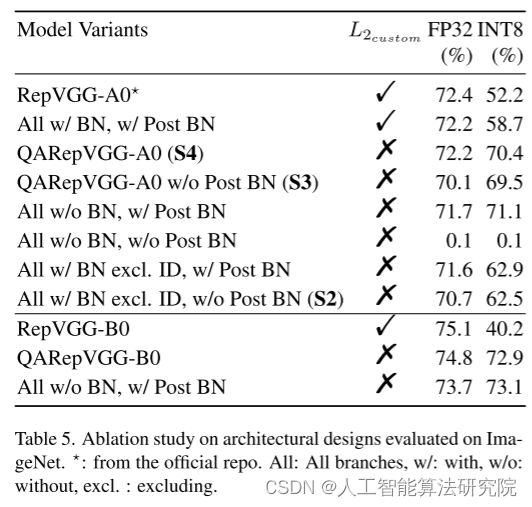
英文论文(sci)解读复现【NO.5】让RepVGG再次变得更强大:一种量化感知方法
此前出了目标检测算法改进专栏,但是对于应用于什么场景,需要什么改进方法对应与自己的应用场景有效果,并且多少改进点能发什么水平的文章,为解决大家的困惑,此系列文章旨在给大家解读发表高水平学术期刊中的SCI论文&am…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

门静脉高压——表现
一、门静脉高压表现 00:01 1. 门静脉构成 00:13 组成结构:由肠系膜上静脉和脾静脉汇合构成,是肝脏血液供应的主要来源。淤血后果:门静脉淤血会同时导致脾静脉和肠系膜上静脉淤血,引发后续系列症状。 2. 脾大和脾功能亢进 00:46 …...

GB/T 43887-2024 核级柔性石墨板材检测
核级柔性石墨板材是指以可膨胀石墨为原料、未经改性和增强、用于核工业的核级柔性石墨板材。 GB/T 43887-2024核级柔性石墨板材检测检测指标: 测试项目 测试标准 外观 GB/T 43887 尺寸偏差 GB/T 43887 化学成分 GB/T 43887 密度偏差 GB/T 43887 拉伸强度…...

【Redis】Redis从入门到实战:全面指南
Redis从入门到实战:全面指南 一、Redis简介 Redis(Remote Dictionary Server)是一个开源的、基于内存的键值存储系统,它可以用作数据库、缓存和消息代理。由Salvatore Sanfilippo于2009年开发,因其高性能、丰富的数据结构和广泛的语言支持而广受欢迎。 Redis核心特点:…...

React与原生事件:核心差异与性能对比解析
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...
