【数据结构】排序算法

目录
1.理解排序
1.1 排序的概念
1.2 排序的运用场景
1.3 常见的排序算法
2.插入排序算法
2.1 直接插入排序
2.2 希尔排序
3.选择排序算法
3.1 直接选择排序
3.2 堆排序
4.交换排序算法
4.1 冒泡排序
4.2 快速排序
4.2.1 hoare 法
4.2.2 挖坑法
4.2.3 前后指针法
4.2.4 三数取中法
5.归并排序算法
6. 排序算法复杂度及稳定性分析
1.理解排序
1.1 排序的概念
排序的概念:排序无非就是将一组数据,按照其中某个或者某些关键字的大小,进行从大到小或者从小到大的顺序排列
升序:也称递增,也就是从小到大排序
降序:也称递减,也就是从大到小排序
排序按照稳定性可以分为:稳定性排序和不稳定性排序
- 稳定性排序:假设我们现在有一组数据,数据中有两个相同的元素。排序完后,这两个相同元素的顺序依旧保持原来的顺序(在前面的那个元素,排序完后依旧在另一个的前面),这就是稳定性排序
- 不稳定性排序:假设我们现在有一组数据,数据中有两个相同的元素。排序完后,这两个相同元素的顺序可能会发生变化(在前面的那个元素,排序完后可能在另一个元素的后面),这就是不稳定性排序
排序按照排序所在的地方可以分为:内部排序和外部排序
- 内部排序:数据元素全部放在内存中的排序
- 外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序
1.2 排序的运用场景
例1:我们应该每个人都会用QQ和微信这种通信软件,当我们未设置置顶的时候,它会默认按照别人所发消息的时间进行排序
例2:我们通常都会用淘宝进行购物,当我们点击销量时,它会按照销量进行排序
1.3 常见的排序算法
我们常见的排序算法有七个,分别为:直接插入排序、希尔排序、选择排序、堆排序、冒泡排序、快速排序、归并排序
这七个常见的排序,又可以分为四类,分别为: 插入排序、选择排序、交换排序、归并排序
2.插入排序算法
2.1 直接插入排序
直接插入排序:大家应该都玩过扑克牌,玩扑克牌的时候,大家都会一张一张的拿牌,每拿到一张牌我们都会将其插入到合适的位置,这就是直接插入排序
假设我们现在有一个数组为 {5,2,4,6,1,3} ,现在需要采用直接插入排序算法进行排序
直接插入排序思路:通过循环遍历数组让 end 存放数组第一个元素的下标,tmp 存放的是 end 后面一个元素的值。然后内循环判断 end 是否大于等于 0,如果大于等于 0 则进入内循环,若为升序排序,则判断 tmp 中存放的值是否小于 end 下标对应的值,如果时则将 end 下标对应的值放在 end+1 下标位置上(往后移),然后让 end--,若 end<0 就跳出循环, 如果 tmp 中存放的值不小于 end 下标对应的值。跳出内循环后让 end+1 下标对应数组元素等于 tmp。然后使 end 指向第二个元素的下标,同样的方法依次比较。
//直接插入排序
public void insertSortDirectly(int[] arr) {for (int i = 0; i < arr.length - 1; i++) {int end = i;int tmp = arr[end + 1];while (end >= 0) {if (tmp < arr[end]) {arr[end + 1] = arr[end];end--;} else {break;}}arr[end + 1] = tmp;}
}直接插入排序的特性总结:
- 当元素集合越接近有序,直接插入排序算法的时间效率越高
- 时间复杂度:O(N^2)
- 空间复杂度:O(1),它是一种稳定的排序算法
- 稳定性:稳定
2.2 希尔排序
希尔排序法又称缩小增量法其实相当于直接插入排序的进阶版,它比直接插入排序多了预排序
希尔排序分为两步:预排序(让数据接近有序),直接插入排序(让数据有序)
希尔排序思想:先选定一个整数存放在 gap 变量中,把待排序数据按照 gap 大小分成组,所有距离为 gap 的分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工作。当到达 gap=1 时,所有数据在统一组内排好序。
假设我们现在有一个数组为 {5,2,4,6,1,3} ,现在需要采用希尔排序算法进行排序
//希尔排序
public void shellSort(int[] arr) {int gap = arr.length;//预排序while (gap > 1) {gap = gap / 2;for (int i = 0; i < arr.length - gap; i++) {int end = i;int tmp = end + gap;while (end >= 0) {if (tmp < arr[end]) {arr[end + gap] = arr[end];end = end - gap;} else {break;}}arr[end + gap] = tmp;}}
}gap值应该如何设定?
gap值通常设为数据长度的一半,然后依次除 2。当 gap 不为 1 时都为预排序,当 gap 为 1 时就是直接插入排序
希尔排序的特性总结:
- 希尔排序是对直接插入排序的优化
- 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,就是直接插入排序。它与直接插入排序的区别就是多了一个预排序,这样使时间效率更好
- 希尔排序的时间复杂度不好计算,需要进行推导,推导出来平均时间复杂度: O(N^1.3— N^2)
- 稳定性:不稳定
3.选择排序算法
选择排序:每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在未排序序列的起始位置,直到全部待排序的数据元素排完即可
3.1 直接选择排序
直接选择排序: 每一次从待排序的数据元素中选出最小(或最大)的一个元素,与未排序序列的起始位置交换,直到全部待排序的数据元素排完即可
//直接选择排序
public void directSelectSort(int[] arr) {for (int i = 0; i < arr.length; i++) {int min = i;for (int j = i + 1; j < arr.length; j++) {if (arr[j] < arr[min]) {min = j;}}int tmp = arr[i];arr[i] = arr[min];arr[min] = tmp;}
}除了上面的每次使一个元素归位以外,还可以每次使两个元素归位,每次遍历找到最小的和未排序的第一个元素交换,找到最大的和未排序的最后一个元素交换
public void directSelectSort(int[] arr) {for (int i = 0; i < arr.length; i++) {int min = i;int max = i;for (int j = i + 1; j < arr.length; j++) {if (arr[j] < arr[min]) {min = j;}if (arr[j] > arr[max]) {max = j;}}int tmp = arr[i];arr[i] = arr[min];arr[min] = tmp;if (max == i) {max = min;}}
}但是需要注意一个问题就是当待排序的数据元素中第一个是最大值时,应该怎么办?
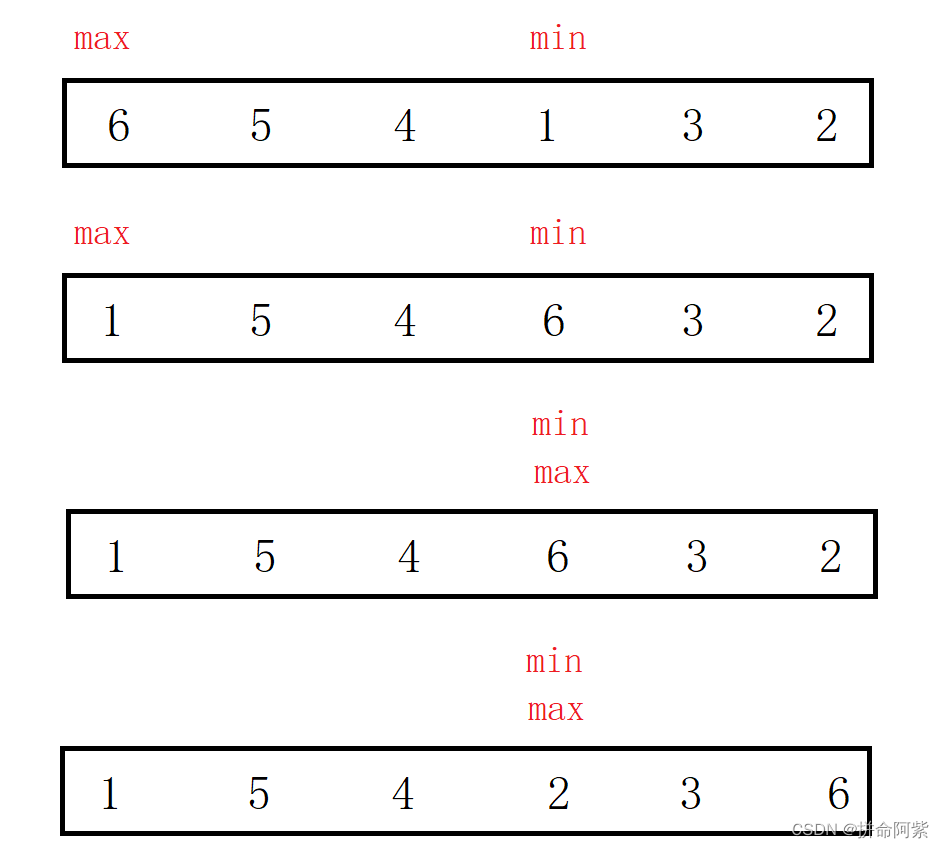
当待排序的数据元素中第一个是最大值时,在将待排序中最小的值与待排序第一个值交换后,还需要将 max 等于 min
直接选择排序的特性总结:
- 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:不稳定
3.2 堆排序
在上一篇文章中我们已经学习了堆,大家也了解了什么是堆,也模拟实现了堆,那接下来我们就来看看如何采用堆来进行排序
如果想要进行堆排序首先需要构造一个堆,如果是升序就构大堆,降序就构小堆
然后构造好堆后,让堆顶元素与最后一个有效元素交换位置,那么最后一个有效元素也就排好序了,将有效元素减一,在向下调整创建堆。然后依次这样交换向下调整知道所有位置的元素都排好序
假设我们现在有一组数据,需要将其排升序
//堆排序
public void heapSort(int[] arr) {buildHeap(arr);//建堆int size = arr.length - 1;int first = 0;while (first < size) {int tmp = arr[first];arr[first] = arr[size];arr[size] = tmp;size--;shiftDown(arr,first ,size+1);}
}
//建堆
public void buildHeap(int[] arr) {if (arr == null) {return;}int lastNoLeafNode = (arr.length - 1 - 1) / 2;while (lastNoLeafNode >= 0) {shiftDown(arr,lastNoLeafNode,arr.length);lastNoLeafNode--;}
}//向下调整,建大顶堆
public void shiftDown(int[] arr, int parent, int size) {int child = parent * 2 + 1;while (child < size) {if (child + 1 < size && arr[child + 1] > arr[child]) {child += 1;}if (arr[parent] >= arr[child] ) {break;} else {int tmp = arr[parent];arr[parent] = arr[child];arr[child] = tmp;parent = child;child = parent * 2 + 1;}}
}堆排序的特性总结:
- 堆排序使用堆来选数,效率就高了很多。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(1)
- 稳定性:不稳定
4.交换排序算法
交换排序基本思想:所谓交换排序,也就是将数据序列中的两个数据值进行比较,满足条件则进行交换,主要思想就是要进行交换
升序排序:就把数据值大的向后移动,数据值小的向前移动
降序排序:就把数据值小的向后移动,数据值大的向前移动
4.1 冒泡排序
冒泡排序的思想:每比较一趟就会使一个值进行归位,所以一共要比较 n-1 趟,才能使全部数据归位
假设现在有这样一组数据序列 {2,5,4,6,3,1},要通过冒泡排序算法来进行排序
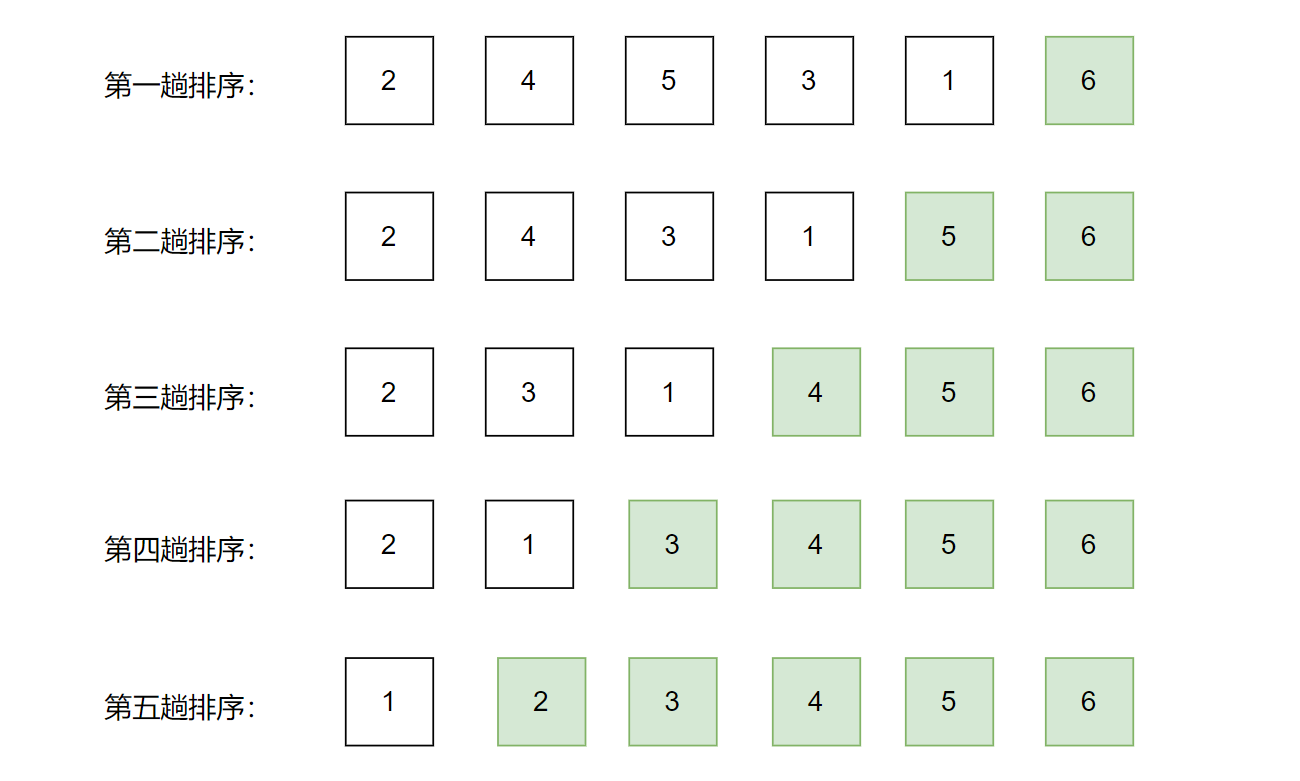
//冒泡排序
public void bubbleSort(int[] arr) {for (int i = 0; i < arr.length - 1; i++) {for (int j = 1; j < arr.length - i; j++) {if (arr[j - 1] > arr[j]) {int tmp = arr[j - 1];arr[j - 1] = arr[j];arr[j] = tmp;}}}
}如果我们数据序列本来就是有序的,难道我们还需要比较 n-1 趟嘛?
答:不需要,我们直接用一个变量来记录是否交换了数据,如果比较完一趟后并没有发生交换直接跳出即可
冒泡排序的特性总结:
- 冒泡排序是一种非常容易理解的排序
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
4.2 快速排序
快速排序基本思想:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止
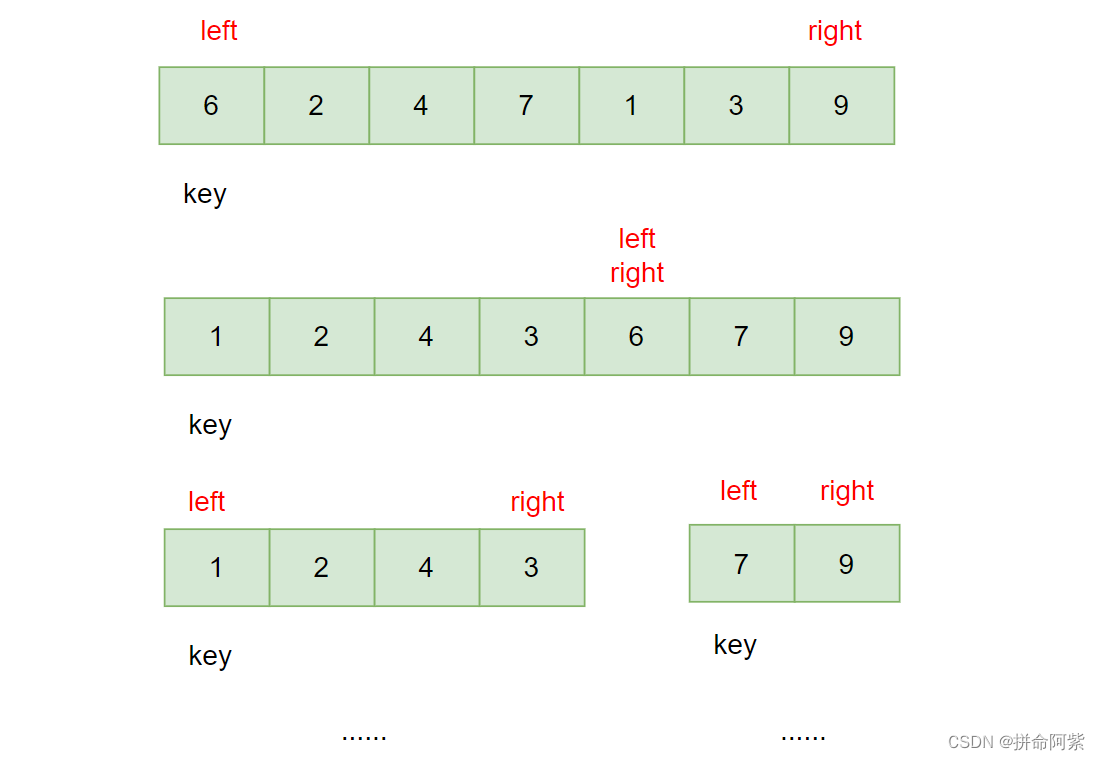
public void quickSort(int[] arr,int left,int right) {if (left >= right) {return;}//调用快速排序int mid = hoareSort(arr,left,right);quickSort(arr,left,mid-1);quickSort(arr,mid + 1,right);}上述是采用递归的方法来调用快速排序算法,首先将一个大排序通过递归分成一些小排序来进行排序
那接下来我们就学习三种快速排序算法,分别是hoare法、挖坑法、左右指针法
4.2.1 hoare 法

基准值key通常指向第一个位置,然后从右边找比基准值小的值,左边找比基准值大的值,找到之后进行交换,当 left 和 right 指向同一个地方说明基准值的最终位置找到
public int hoareSort(int[] arr,int left,int right) {int key = left;while (left < right) {while (left < right && arr[right] >= arr[key]) {right--;}while (left < right && arr[left] <= arr[key]) {left++;}swap(arr,left,right);}swap(arr,key,left);return left;
}public void swap(int[] arr,int left,int right) {int tmp = arr[left];arr[left] = arr[right];arr[right] = tmp;
}4.2.2 挖坑法

首先将第一个值当作基准值放入 key 中,那么第一个位置就形成了一个坑,从右边找比基准值小的放入左边的坑中,那么右边的这个位置也就形成了一个坑,再从左边找比基准值大的放入右边的坑中,最后 left 和 right 同时指向的地方就是基准值最终的位置
public int digPitSort(int[] arr,int left,int right) {int key = arr[left];while (left < right) {while (left < right && arr[right] >= key) {right--;}arr[left] = arr[right];while (left < right && arr[left] <= key) {left++;}arr[right] = arr[left];}arr[left] = key;return left;
}4.2.3 前后指针法
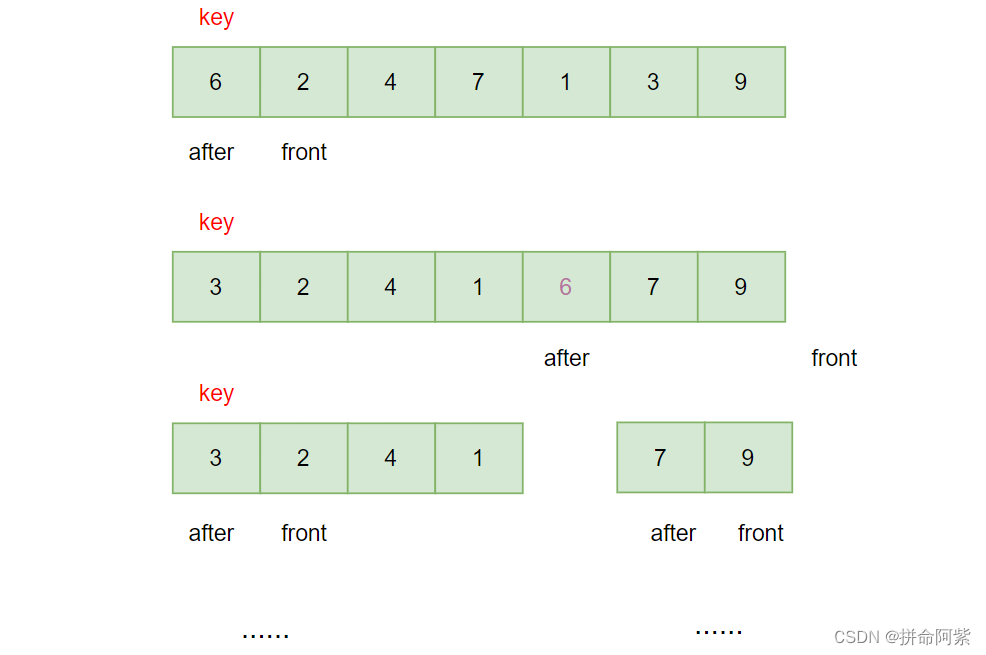
首先将第一个值当作基准值将其下标放入 key 中,然后让 after 存放第一个元素的下标,front 存放第二个元素的下标,front < right 就进入循环,然后判断 front 下标里面的元素是否小于基准值,如果小于再判断 ++after 是否不等于基准值,如果满足就进行交换,然后再 front++ 。直到 front 不小于 right 不进入循环,然后将基准值与 after 的位置交换,基准值归位。
//前后指针法
public int frontBack(int[] arr,int left,int right) {int key = left;int after = left;int front = left + 1;while (front <= right) {if (arr[front] < arr[key] && arr[++after] != arr[key]) {swap(arr,after,front);}front++;}swap(arr,key,after);return after;
}public void swap(int[] arr,int after,int front) {int tmp = arr[after];arr[after] = arr[front];arr[front] = tmp;
}4.2.4 三数取中法
当序列为有序的时候,快速排序的时间复杂度为 O(N^2)
为了避免这种情况也就可以采用三数取中法
三数取中法思路:对比第一个下标的数和中间下标的数与最后下标的数,返回中间数(不是最大也不是最小)
//三数取中法
public int getMidIndex(int[] arr,int left,int right) {int mid = (left + right) >> 1;if (arr[left] < arr[mid]){if (arr[mid] < arr[right]) {return mid;} else if (arr[left] > arr[right]) {return left;} else {return right;}} else {if (arr[mid] > arr[right]) {return mid;} else if (arr[left] < arr[right]) {return left;} else {return right;}}
}快速排序的特性总结:
- 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
- 时间复杂度:O(N*logN)
- 空间复杂度:O(logN)
- 稳定性:不稳定
5.归并排序算法
归并排序基本思想: 归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
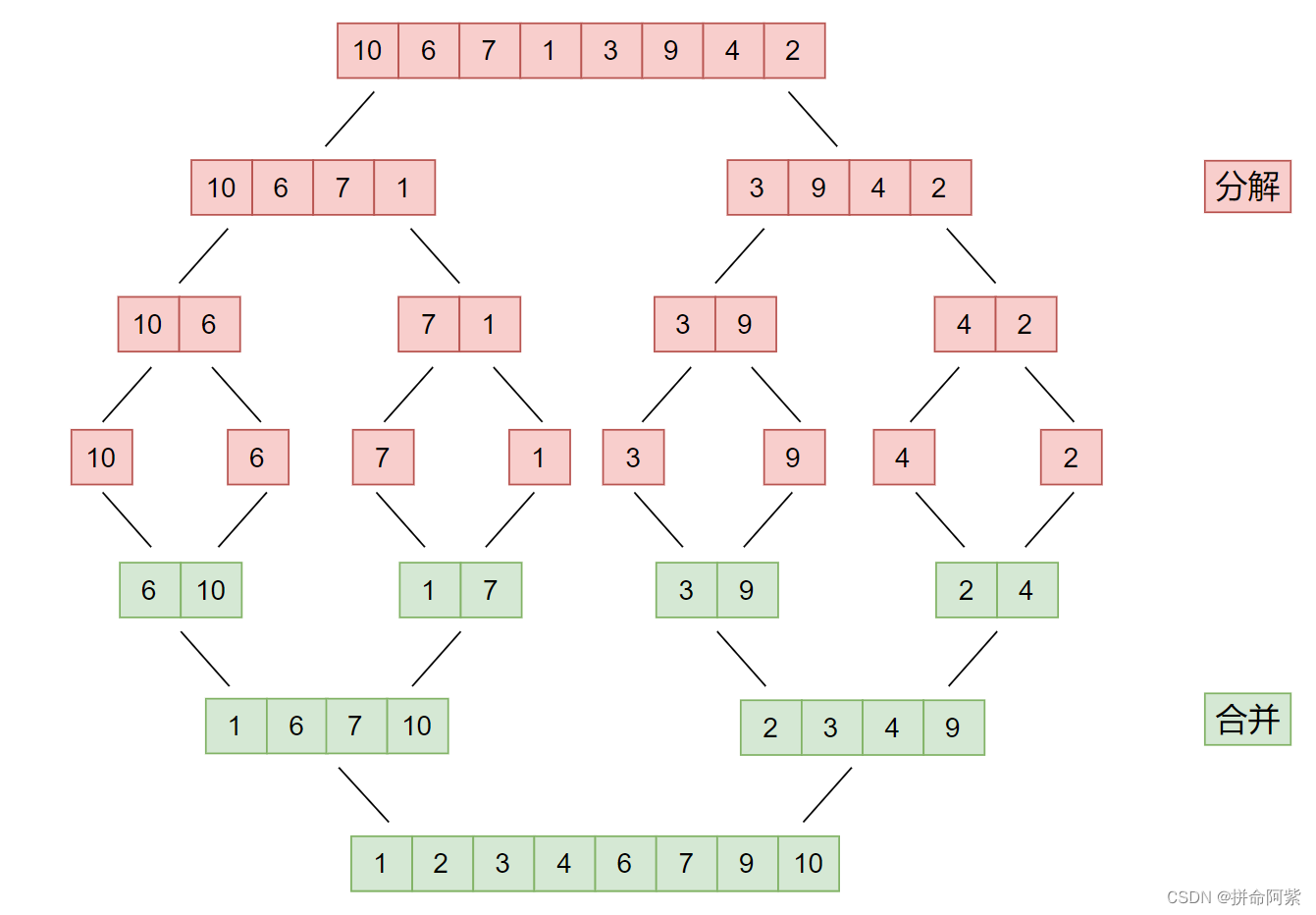
//归并排序
public void mergeSort(int[] arr,int left,int right) {//分解if (left >= right) {return;}int mid = (left + right) / 2;mergeSort(arr,left,mid);mergeSort(arr,mid+1,right);//合并merge(arr,left,mid,right);
}
public void merge(int[] arr,int left,int mid,int right) {int s1 = left;int s2 = mid + 1;int[] ret = new int[(right - left) + 1];int i = 0;while (s1 <= mid && s2 <= right) {if (arr[s1] <= arr[s2]) {ret[i++] = arr[s1++];} else {ret[i++] = arr[s2++];}}while (s1 <= mid) {ret[i++] = arr[s1++];}while (s2 <= right) {ret[i++] = arr[s2++];}for (int j = 0; j < ret.length; j++) {arr[j+left] = ret[j];}
}归并排序的特性总结:
- 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
6. 排序算法复杂度及稳定性分析
| 排序方法 | 最好情况 | 平均情况 | 最坏情况 | 空间复杂度 | 稳定性 |
| 冒泡排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 插入排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 |
| 希尔排序 | O(n) | O(n^1.3) | O(n^2) | O(1) | 不稳定 |
| 堆排序 | O(n * log(n)) | O(n * log(n)) | O(n * log(n)) | O(1) | 不稳定 |
| 快速排序 | O(n * log(n)) | O(n * log(n)) | O(n^2) | O(log(n)) ~ O(n) | 不稳定 |
| 归并排序 | O(n * log(n)) | O(n * log(n)) | O(n * log(n)) | O(n) | 稳定 |
相关文章:

【数据结构】排序算法
目录 1.理解排序 1.1 排序的概念 1.2 排序的运用场景 1.3 常见的排序算法 2.插入排序算法 2.1 直接插入排序 2.2 希尔排序 3.选择排序算法 3.1 直接选择排序 3.2 堆排序 4.交换排序算法 4.1 冒泡排序 4.2 快速排序 4.2.1 hoare 法 4.2.2 挖坑法 4.2.3 前…...

[MySQL]初识数据库
哈喽,大家好!我是保护小周ღ,本期为大家带来的是 MySQL 数据库,也是新的知识,首先我们会初步认识什么是数据库,什么是Mysql 数据库,以及我们 mysql 主要学什么,SQL 语句简单使用&…...
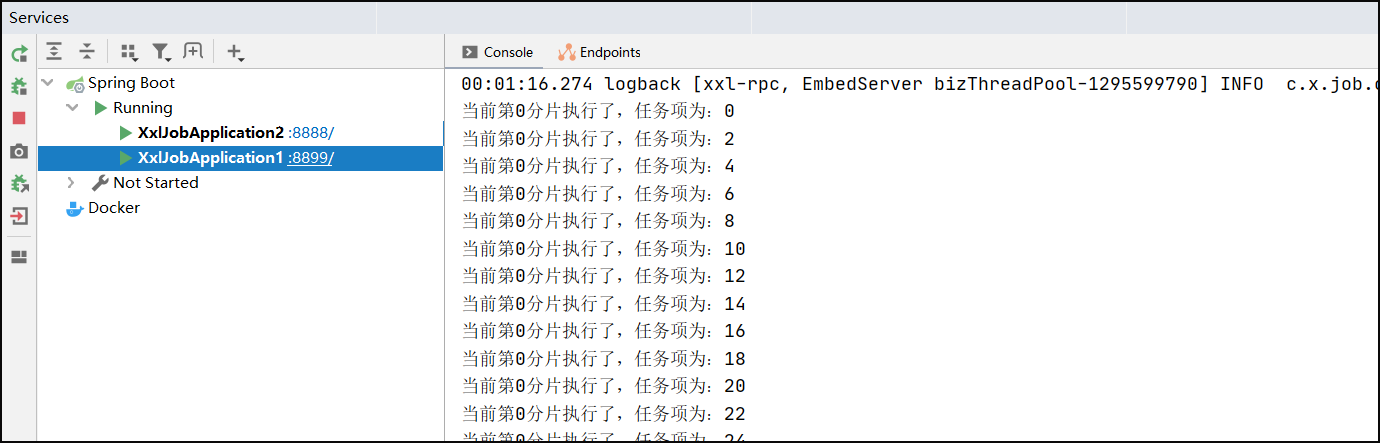
XXL-JOB分布式任务调度框架(二)-路由策略
文章目录1.引言2.任务详解2.1.执行器2.2.基础配置3.路由策略(第一个)-案例4.路由策略(最后一个)-案例5.轮询策略-案例7.分片广播任务1.引言 本篇文章承接上文《XXL-JOB分布式任务调度框架(一)-基础入门》,上一次和大家简单介绍了下 xxl-job 的由来以及使用方法&…...
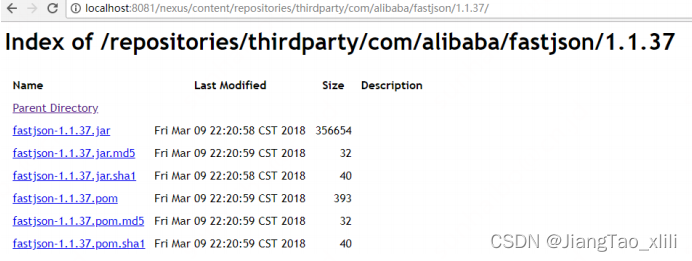
Java_Maven:5. 把第三方 jar 包放入本地仓库或私服
目录 1 导入本地库 2 导入私服 3 参数说明 1 导入本地库 随便找一个 jar 包测试,可以先 CMD进入到 jar 包所在位置,运行 mvn install:install-file -DgroupIdcom.alibaba -DartifactIdfastjson -Dversion1.1.37-Dfile fastjson-1.1.37.jar -Dpackaging…...
)
【剑指offer】03~05. 数组中的数字(C# 实现)
文章目录前言03. 数组中重复的数字04. 二维数组中的查找05. 替换空格结语前言 😃 大家好,我是writer桑,这是自己整理的 C# 做题记录,方便自己学习的同时分享出来,感谢支持。 03. 数组中重复的数字 题目描述࿱…...
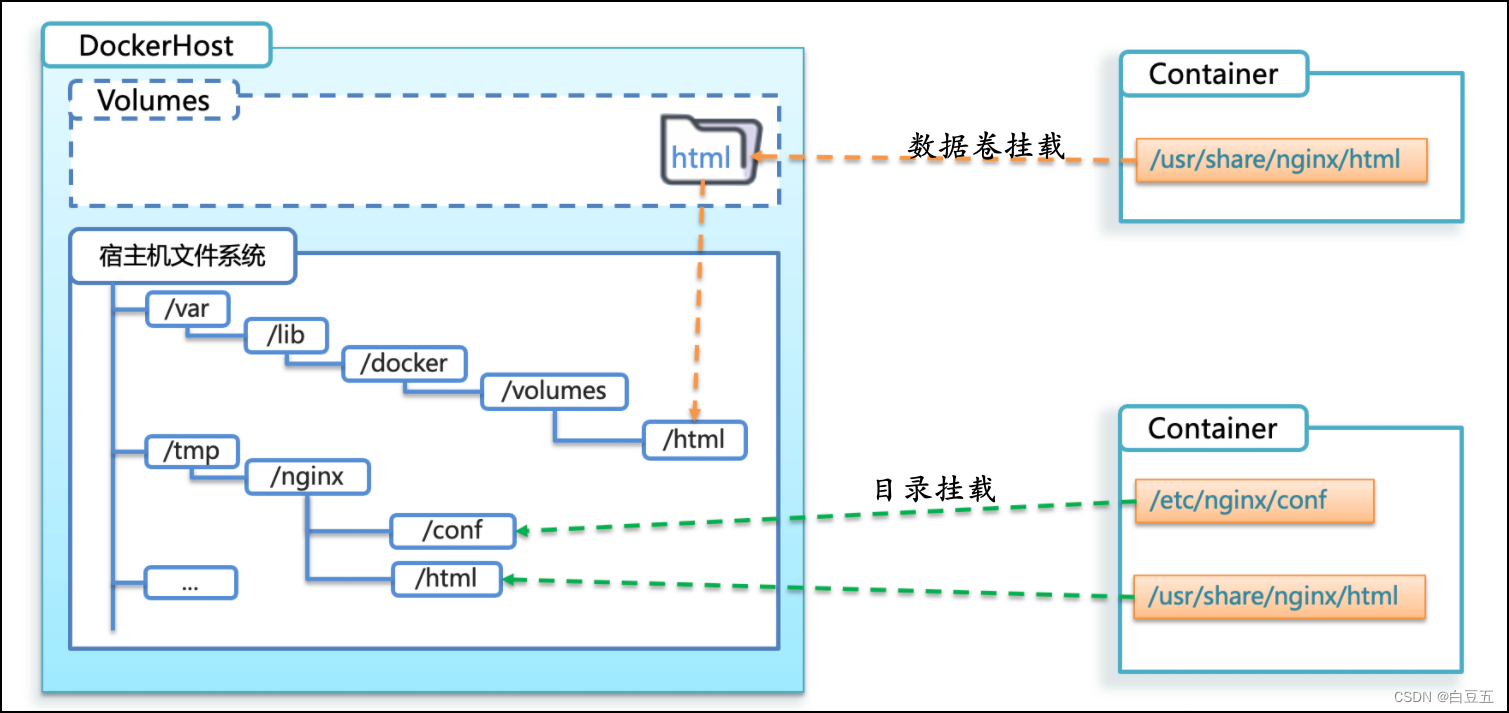
Docker入门教程
文章目录一、Docker概述1. 什么是容器技术?2. 什么是Docker3. 为什么要使用Docker4. Docker和虚拟机的对比5. Docker相关概念6. DockerHub7. Docker架构二、安装Docker1. 安装Docker2. 配置阿里云镜像加速三、Docker常用命令1. 帮助命令2. 镜像操作命令3. 容器操作命…...
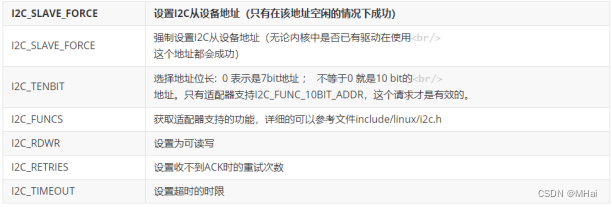
I2C总线应用测试程序
参考链接:I2c协议 Linux I2C应用编程开发 问题背景 在工作中需要测试I2C总线的传输稳定性,需写一个测试程序通过读写从设备寄存器的值来验证数据传输稳定性。 站在cpu的角度来看,操作I2C外设实际上就是通过控制cpu中挂载该I2C外设的I2C控制…...

主从表的建立
//表查--病害id--主从表public static DataSet QueryGetQlgjDispdbdisidTABbyqidZC(string qid, string bwname){string SQLStringZ "select * from tl_qlsoft_cql_qlcheck_qlstye_bw a, tl_qlsoft_cql_qlcheck_qlstye_bw_gj b where a.chbwidb.chbwid and a.qli…...
)
Exporter介绍与指标数据,规范说明(更新中)
1.exporter是什么广义上讲所有可以向Prometheus提供监控样本数据的程序都可以被称为一个Exporter。而Exporter的一个实例称为target,如下所示,Prometheus通过轮询的方式定期从这些target中获取样本数据:2.exporter的来源与分类从Exporter的来源上来讲&am…...

[Android Studio] Android Studio Virtual Device虚拟机的功能试用
🟧🟨🟩🟦🟪 Android Debug🟧🟨🟩🟦🟪 Topic 发布安卓学习过程中遇到问题解决过程,希望我的解决方案可以对小伙伴们有帮助。 🚀write…...
)
华为OD机试 - 检查数组中是否存在满足规则的数组组合1(Python)
检查数组中是否存在满足规则的数组组合1 题目 给定一个正整数数组 检查数组中是否存在满足规则的数组组合 规则: A = B + 2C 输入 第一行输出数组的元素个数 接下来一行输出所有数组元素,用空格隔开 输出 如果存在满足要求的数 在同一行里依次输出规则里A B C的取值,用…...

深圳“托育”放大招!政府出钱帮你带娃啦!
工作忙得不可开交 难以照料孩子的起居 这个带娃难题常常让双职工家庭 感觉到头疼不已 一边是工作,一边是孩子 父母都上班,宝宝谁来带? 未来这个问题将迎刃而解! 因为政府要出钱帮你带娃啦! 近日,深圳市总工…...

服务间调用方式 OpenFeign 的介绍和使用
文章目录前言1、 RestTemplate1.1、通用方法 exchange1.2、RestTemplate 和 OpenFeign 的区别2、RPC 和 HTTP2.1、RPC 是什么2.2、RPC 调用过程示意图2.3、HTTP 是什么2.4、HTTP 调用过程示意图2.5、对比3 、OpenFeign3.1 、OpenFeign 常用注解3.2 、案例前言 Feign 停更了&am…...
从开始测试到年薪40W,我的自动化测试艰辛历程
我希望我的故事能够激励现在的软件测试人,尤其是还坚持在做“点点点”的测试人。 你可能会有疑问:“我也能做到这一点的可能性有多大?”因此,我会尽量把自己做决定和思考的过程讲得更具体一些,并尽量体现更多细节。 …...
)
《C++ Primer Plus》第17章:输入、输出和文件(1)
对C输入和输出(简称I/O)的讨论提出了一个问题。一方面,几乎每个程序都要使用输入和输出,因此了解如何使用它们是每个学习计算机语言的人面临的首要任务;另一方面,C使用了很多较为高级的语言特性来实现输入和…...
静态代码审计插件 snyk 使用教程
目录 1、vscode 插件安装 2、手动生成 token 3、自动分析 1、vscode 插件安装 2、手动生成 token 点击登录链接:...

从“服务”,到“赋能”,日日顺再次定义供应链生态建设
在众多不确定因素的交织下,当下的供应链企业变革呈现出前所未有的紧迫感。一体化、全链路的趋势,为企业的发展指明方向,与此同时数字化与科技化开始承托供应链管理能力的升级与变革。 2月15日,由日日顺供应链、运联智库联合举办的…...
MySQL(一):B+ Tree,索引以及其优点, 索引实战, 聚簇索引和非聚簇索引, 最左匹配,索引失效
文章目录一、B TreeB Tree相比于红黑树的优点1. B树有更低的树高2. B树更符合磁盘访问原理二、MySQL索引2.1 B Tree索引2.2 哈希索引2.3 全文索引2.4 空间数据索引三、索引的优点以及什么时候需要使用索引什么时候需要使用索引四、索引实战建立普通索引建立唯一索引建立主键索引…...

06:进阶篇 - Hello,CTK!
作者: 一去、二三里 个人微信号: iwaleon 微信公众号: 高效程序员 在接触任何语言时,我们总能看到“Hello,World!",它的中文意思是“你好,世界!”。由于简洁、实用,所以非常著名。 为了延续这个优良传统并迎接 CTK,在演示第一个插件时,我们使用“Hello,CTK!&qu…...

SpringCloud(一)注册中心
注册中心eureka服务端客户端负载均衡nacos服务端客户端nacos分级存储模型配置集群属性nacos环境隔离-namespace临时实例和非临时实例Eureka和Nacos的异同负载均衡策略饥饿加载eureka 服务端 依赖 <!-- eureka注册中心服务端依赖--><dependencies><depe…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...

从实验室到产业:IndexTTS 在六大核心场景的落地实践
一、内容创作:重构数字内容生产范式 在短视频创作领域,IndexTTS 的语音克隆技术彻底改变了配音流程。B 站 UP 主通过 5 秒参考音频即可克隆出郭老师音色,生成的 “各位吴彦祖们大家好” 语音相似度达 97%,单条视频播放量突破百万…...
