【数据结构】平衡二叉树

目录
一、平衡二叉树的介绍
二、平衡二叉树的插入
1、平衡二叉树的插入步骤
2、平衡二叉树的旋转
2.1左单旋
2.2右单旋
2.3左右双旋
2.4右左双旋
三、平衡二叉树的删除(略)
四、个人对平衡二叉树见解
五、平衡二叉树整体代码
一、平衡二叉树的介绍
二叉搜索树的目的是为了提高查找效率,但如果数据有序或者接近有序,那么二叉搜索树将会变成单支树,查找元素的效率等效为顺序表,树形结构的优势荡然无存。
为了解决这一问题,苏联数学家G.M.Adelson-Velskii和E.M.Landis便发明了平衡二叉树(AVL树)。
平衡二叉树:在一棵搜索二叉树中每个节点的左右子树的高度差的绝对值不超过1。左右子树的高度差被称为平衡因子(平衡因子=右子树高度-左子树高度)。若一颗平衡二叉树的节点个数为n,那么其高度为logN。
二、平衡二叉树的插入
1、平衡二叉树的插入步骤
平衡二叉树的插入第一步和二叉搜索树一样,根据二叉搜索树的特性,找到新插入节点位于整棵树的位置。
随后使用逻辑语句判断新节点是插入在父节点的左还是右,并维护其与父节点的指针关系。
新增在右,平衡因子++;新增在左,平衡因子--。那新插入了一个节点,原先的平衡二叉树的结构可能会遭到破坏,所以需要观察平衡因子的三种情况,进行分类讨论:如图
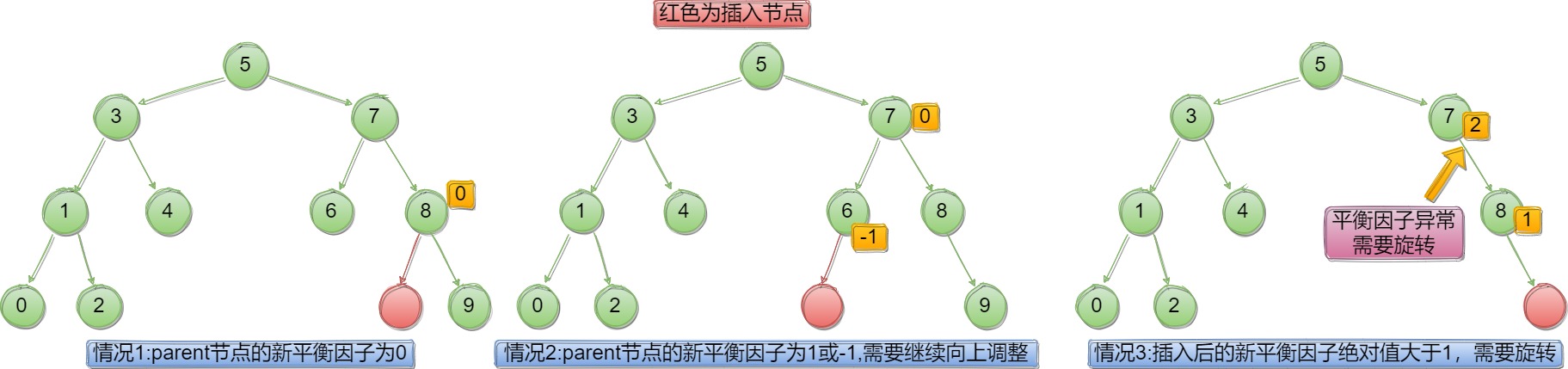
情况三如何旋转?无非是四种情况:
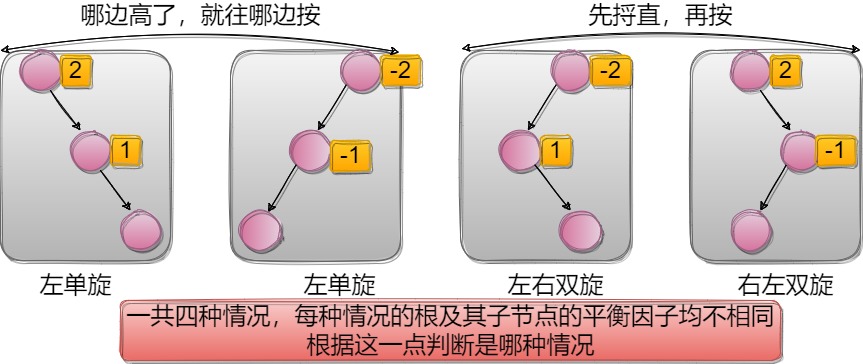
2、平衡二叉树的旋转
当出现上图情况三时,就需要对平衡二叉树的节点进行旋转,旋转的目的是要让这颗树继续维持平衡二叉树的形态,同时调节子树的高度,让其和插入前的高度保持一致,旋转后不要忘记更新那些被旋转的节点的平衡因子。
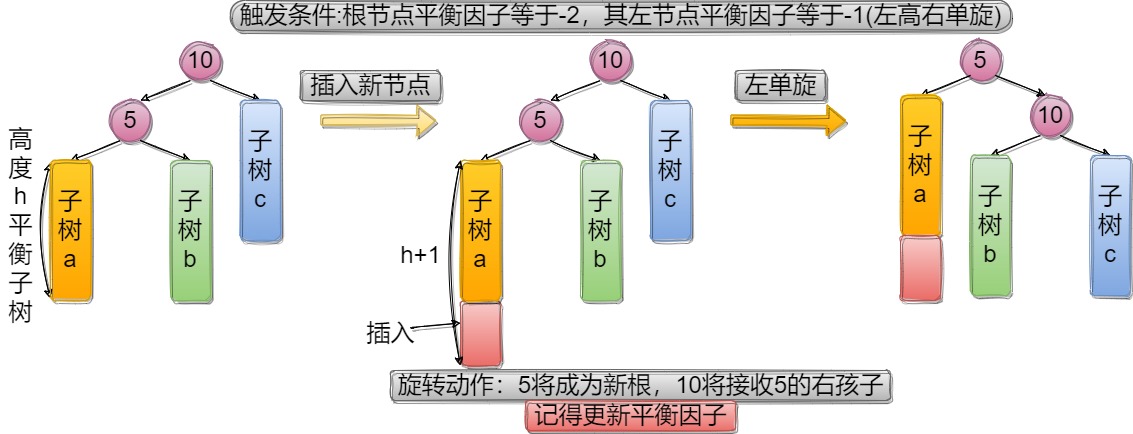
2.1左单旋

5可能是根,也可能是某颗子树的根,分类讨论:
void RotateLeft(Node* parent)//左单旋
{Node* grandfather = parent->_parent;Node* cur = parent->_right;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (grandfather->_left == parent)//需要判定parent原来属于grandfather的哪一边grandfather->_left = cur;elsegrandfather->_right = cur;cur->_parent = grandfather;}parent->_right = cur->_left;if (cur->_left != nullptr)cur->_left->_parent = parent;cur->_left = parent;parent->_parent = cur;//更新平衡因子cur->_bf = parent->_bf = 0;
}2.2右单旋
void RotateRight(Node* parent)//右单旋
{Node* grandfather = parent->_parent;Node* cur = parent->_left;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (grandfather->_left == parent){grandfather->_left = cur;cur->_parent = grandfather;}else{grandfather->_right = cur;cur->_parent = grandfather;}}parent->_parent = cur;parent->_left = cur->_right;if (cur->_right != nullptr)cur->_right->_parent = parent;cur->_right = parent;//更新平衡因子cur->_bf = parent->_bf = 0;
}2.3左右双旋

void RotateLR(Node* parent)//左右双旋
{Node* cur = parent->_left;Node* curR = cur->_right;int bf = curR->_bf;RotateLeft(parent->_left);RotateRight(parent);if (bf == -1)//curR的左树插入新节点{cur->_bf = 0;parent->_bf = 1;curR->_bf = 0;}else if (bf == 1)//curR的右树插入新节点{cur->_bf = -1;parent->_bf = 0;curR->_bf = 0;}else if (bf == 0)//curR自身为新增节点{cur->_bf = 0;parent->_bf = 0;curR->_bf = 0;}elseassert(false);//不可能出现这种情况
}2.4右左双旋
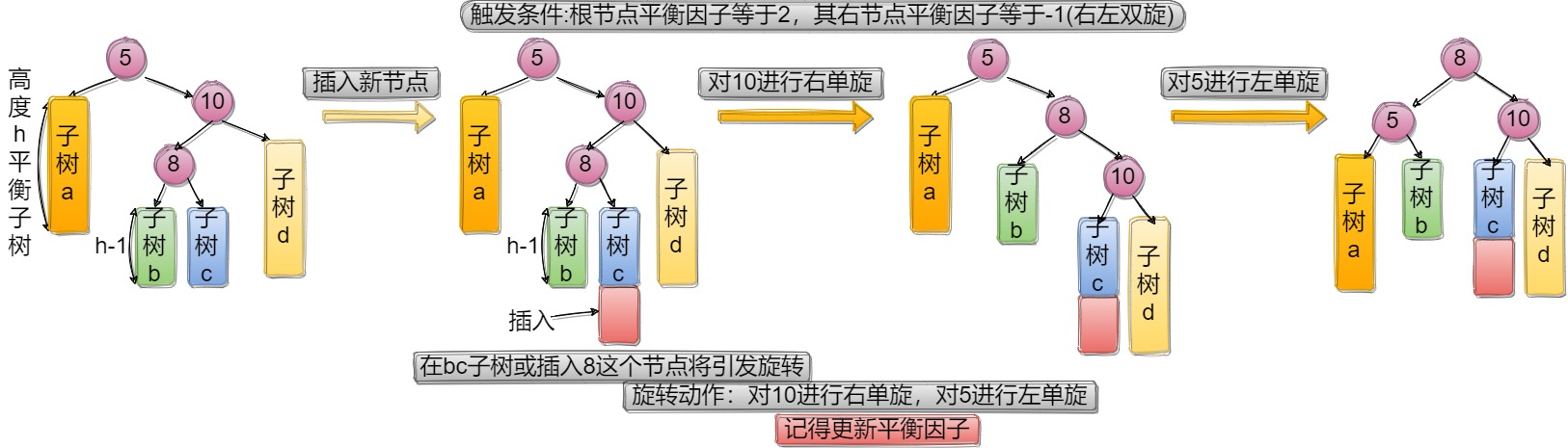
void RotateRL(Node* parent)//右左双旋
{Node* cur = parent->_right;Node* curL = cur->_left;int bf = curL->_bf;RotateRight(parent->_right);RotateLeft(parent);if (bf == -1)//curL的左树插入新节点{cur->_bf = 1;parent->_bf = 0;curR->_bf = 0;}else if (bf == 1)//curL的右树插入新节点{cur->_bf = 0;parent->_bf = -1;curR->_bf = 0;}else if (bf == 0)//curL自身为新增节点{cur->_bf = 0;parent->_bf = 0;curR->_bf = 0;}elseassert(false);//不可能出现这种情况
}三、平衡二叉树的删除(略)
按照二叉搜索树的方式对平衡二叉树节点进行删除。更新平衡因子时,平衡因子为1或-1便可以停止向上更新。当平衡因子绝对值大于1时,同样需要进行旋转解决。
四、个人对平衡二叉树见解
平衡二叉树强就强在通过大量的旋转控制整颗树任意一个节点的左右子树高度差不大于1,使树的结构近似完全二叉树,搜索效率为logN。
但偏偏是频繁的旋转,导致其插入删除的效率并不及红黑树,这也是红黑树成为树形容器的原因。
但是一颗树仅用来查找而不进行删除的话,用平衡二叉树还是很棒的。
五、平衡二叉树整体代码
#pragma once
#include <iostream>
#include <cassert>
#include <map>
#include <set>
#include <time.h>
using namespace std;template <class K, class V>
struct AVLTreeNode
{pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf;//Balance factor平衡因子AVLTreeNode(const pair<K, V>& kv): _kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _bf(0){}
};template <class K, class V>
struct AVLTree
{typedef AVLTreeNode<K, V> Node;//记住不要把这个<K,V>漏了!!!
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}//_root不为空Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else//相等说明元素相同,插入失败return false;}//开始插入cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;//维护cur的父指针}else{parent->_left = cur;cur->_parent = parent;}//更新平衡因子while (parent)//最坏情况更新到根{if (cur == parent->_left){--parent->_bf;}else if (cur == parent->_right){++parent->_bf;}//平衡因子更新完毕后,分析三种情况if (parent->_bf == 0)//父节点的平衡因子为零说明已经平衡break;else if (parent->_bf == 1 || parent->_bf == -1)//一边高一边低{//需要继续向上对平衡因子进行调整cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2)//父节点的平衡因子为2或-2,不满足平衡二叉树规则{//需要旋转调整if (parent->_bf == 2 && cur->_bf == 1)//触发左单旋条件{RotateLeft(parent);//左单旋}else if (parent->_bf == -2 && cur->_bf == -1)//触发右单旋条件{RotateRight(parent);//右单旋}else if (parent->_bf == -2 && cur->_bf == 1)//触发左右双旋{RotateLR(parent);//左右双旋}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);//右左双旋}else{assert(false);}break;//必定平衡,跳出循环}else//防止出现代码错误导致平衡因子绝对值出现大于3的情况(正常情况不会发生这种现象){assert(false);}}return true;}void RotateLeft(Node* parent)//左单旋{Node* grandfather = parent->_parent;Node* cur = parent->_right;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (grandfather->_left == parent)//需要判定parent原来属于grandfather的哪一边grandfather->_left = cur;elsegrandfather->_right = cur;cur->_parent = grandfather;}parent->_right = cur->_left;if (cur->_left != nullptr)cur->_left->_parent = parent;cur->_left = parent;parent->_parent = cur;//处理平衡因子cur->_bf = parent->_bf = 0;}void RotateRight(Node* parent)//右单旋{Node* grandfather = parent->_parent;Node* cur = parent->_left;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (grandfather->_left == parent){grandfather->_left = cur;cur->_parent = grandfather;}else{grandfather->_right = cur;cur->_parent = grandfather;}}parent->_parent = cur;parent->_left = cur->_right;if (cur->_right != nullptr)cur->_right->_parent = parent;cur->_right = parent;//更新平衡因子cur->_bf = parent->_bf = 0;}void RotateLR(Node* parent)//左右双旋{Node* cur = parent->_left;Node* curR = cur->_right;int bf = curR->_bf;RotateLeft(parent->_left);RotateRight(parent);if (bf == -1)//curR的左树插入新节点{cur->_bf = 0;parent->_bf = 1;curR->_bf = 0;}else if (bf == 1)//curR的右树插入新节点{cur->_bf = -1;parent->_bf = 0;curR->_bf = 0;}else if (bf == 0)//curR自身为新增节点{cur->_bf = 0;parent->_bf = 0;curR->_bf = 0;}elseassert(false);//不可能出现这种情况}void RotateRL(Node* parent)//右左双旋{Node* cur = parent->_right;Node* curL = cur->_left;int bf = curL->_bf;RotateRight(parent->_right);RotateLeft(parent);if (bf == -1)//curL的左树插入新节点{cur->_bf = 1;parent->_bf = 0;curL->_bf = 0;}else if (bf == 1)//curL的右树插入新节点{cur->_bf = 0;parent->_bf = -1;curL->_bf = 0;}else if (bf == 0)//curL自身为新增节点{cur->_bf = 0;parent->_bf = 0;curL->_bf = 0;}elseassert(false);//不可能出现这种情况}int TreeHight(Node* root){if (root == nullptr)return 0;int leftHight = TreeHight(root->_left);int rightHight = TreeHight(root->_right);return leftHight > rightHight ? leftHight + 1 : rightHight + 1;}void Inorder(){_Inorder(_root);}bool IsBalance(){return _IsBalance(_root);}
private:void _Inorder(Node* root){if (root == nullptr)return;_Inorder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_Inorder(root->_right);}bool _IsBalance(Node* root){if (root == nullptr)return true;int leftHight = TreeHight(root->_left);int rightHight = TreeHight(root->_right);//检查平衡因子对不对if (rightHight - leftHight != root->_bf){cout << "平衡因子出现异常" << endl;return false;}//需要递归检查是否平衡return (leftHight - rightHight <= 1 && leftHight - rightHight >= -1)&& _IsBalance(root->_left) && _IsBalance(root->_right);}
private:Node* _root = nullptr;
};
//void TestAVLTree()
//{
// //int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
// //int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
// int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
// //int a[] = { 9,8,7,6,5,4,3,2,1};
// AVLTree<int, int> t;
// for (auto e : a)
// {
// t.Insert(make_pair(e, e));
// }
//
// t.Inorder();
//
// cout << t.IsBalance() << endl;
//}
void TestAVLTree()
{srand((unsigned int)time(0));const size_t N = 1000000;AVLTree<int, int> t;for (size_t i = 0; i < N; ++i){size_t x = rand();t.Insert(make_pair(x, x));//cout << t.IsBalance() << endl;}t.Inorder();cout << t.IsBalance() << endl;
}相关文章:

【数据结构】平衡二叉树
目录 一、平衡二叉树的介绍 二、平衡二叉树的插入 1、平衡二叉树的插入步骤 2、平衡二叉树的旋转 2.1左单旋 2.2右单旋 2.3左右双旋 2.4右左双旋 三、平衡二叉树的删除(略) 四、个人对平衡二叉树见解 五、平衡二叉树整体代码 一、平衡二叉树的…...
Minecraft服务端配置
✨✨前言 ✨✨ 我的世界大家肯定都不陌生,在网易拿下中国区的代理后,很多小伙伴也是都转向了网易版我的世界,网易版我的世界可以说已经做是的十分全面了,使用起来也十分方便,一部分小伙伴也是看重了网易庞大的玩家数量…...

yunUI组件库解析:图片上传与排序组件yImgPro
yunUI是笔者开源的微信小程序功能库。目前其中包含了一些复杂的功能组件。方便使用。未来它将分为组件、样式、js三者合为一体,但分别提供。 本文所用代码皆来源于组件库中的yImgPro组件。详细代码可至github查看。地址: yunUI 。 npm地址:yu…...
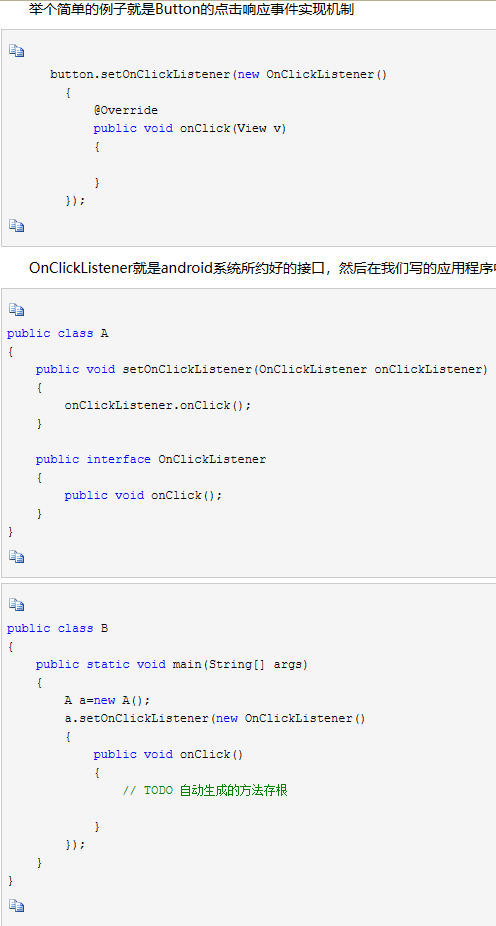
Java基础:回调函数
因为在看Android代码的时候发现了许多关于回调函数的知识, 所以去了解了一下. 对于我来说不太好懂, 因为我觉得看的那些博文的讲法对我来说很绕, 所以我在理解了之后想写一篇关于回调函数的博文来给和我一样理解能力稍差的人一点帮助. 回调函数的作用其实就是将需要这个功能的调…...
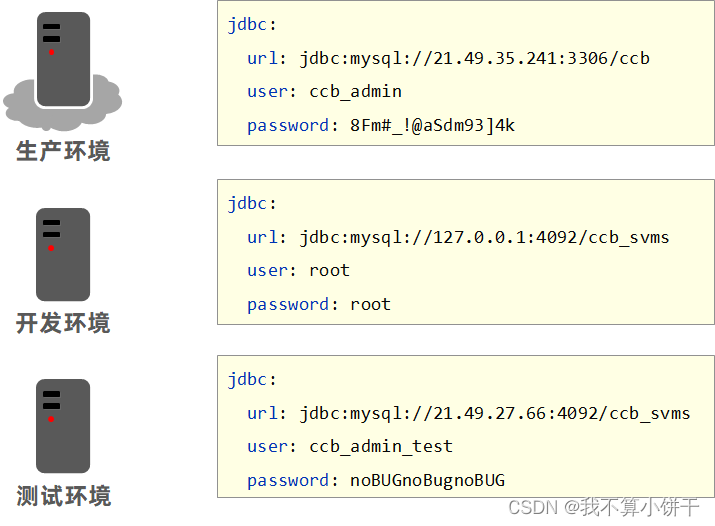
Springboot多环境配置
此文章是根据黑马程序员课程所做的笔记课程视频 多环境开发 什么是多环境?其实就是说你的电脑上写的程序最终要放到别人的服务器上去运行。每个计算机环境不一样,这就是多环境。常见的多环境开发主要兼顾3种环境设置,开发环境——自己用的…...
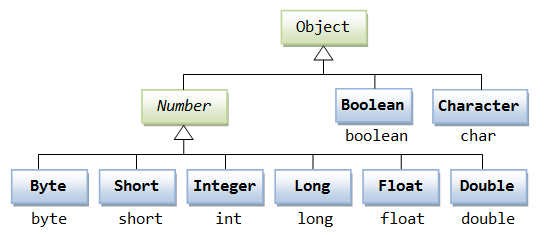
Java Number Math 类,超详细整理,适合新手入门
目录 一、什么是Java Number类? 二、Java Number类提供了哪些基本的数字操作? 三、什么是包装类? 所有的包装类都是抽象类 Number 的子类。 四、什么是Java Math 类 Test类案例:(Math.PI 表示一个圆的周长与直径…...

俯瞰·明统系列·落霞与孤鹜齐飞、南征与北伐并举
尽江南百万兵,腰间宝剑血尤腥。 引言 元至正二十七年(1367年)四月,吴王朱元璋命中书右丞相徐达为征虏大将军、平章常遇春为副将军,率军25万由淮入河、北进中原(第一次北伐)。北伐中发布告北方官…...

Nodejs环境搭建和配置
Nodejs环境的搭建和配置 1、下载 官网:http://nodejs.cn/download/,选择windows64位 msi文件 2、安装和配置环境 双击安装之后,配置环境变量: ①系统变量那边创建NODE_PATH变量,值为nodejs文件夹的node_modules文…...
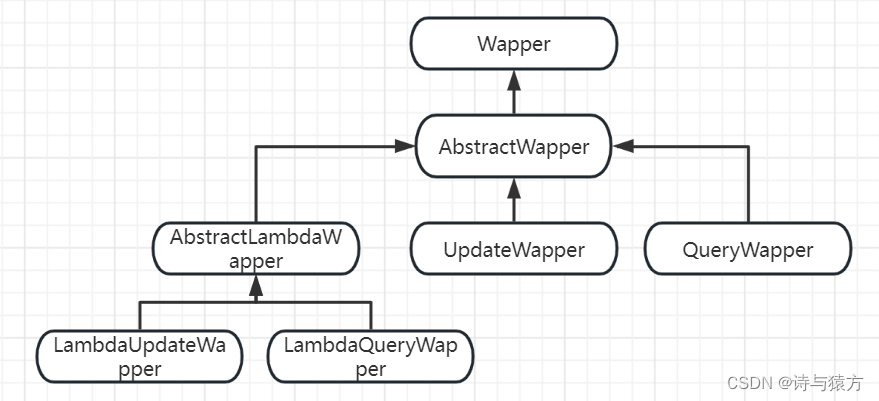
MybatisPlus------条件构造器Wrapper以及QueryWrapper用法(七)
MybatisPlus------条件构造器Wapper(七) Wrapper:条件构造器抽象类,最顶端父类 AbstarctWrapper:用于查询条件封装,生成sql的where条件。 QueryWrapper:查询条件封装(可以用于查询、删除&#x…...
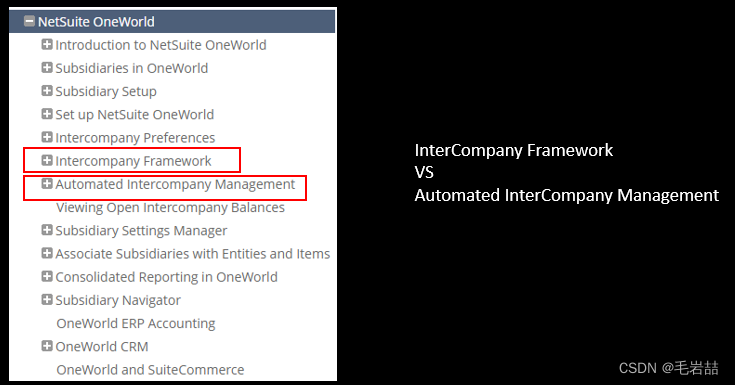
NetSuite Intercompany Framework 101
今朝,谈一谈Intercompany Framework,这是一个彰显NetSuite市场野心的基础功能框架。从20.2开始逐渐浮出水面,虽然经过过往的几个版本,不断推出组成功能,但目前仍然未见其全貌。 作为顾问,你必须关注它&…...

限时活动|凭徽章领披萨大奖,玩转Moonbeam治理论坛
动动手指,无需每天打卡,用刷手机的零碎时间领一份Web3惊喜! 本次挑战的目标是鼓励大家参与社区治理、熟悉论坛操作。有关参与方式和原因的信息在Twitter上共享:有兴趣可以和ThinkWildCrypto一起探索论坛以解锁其功能、了解最近和正…...

Golang中struct{}和struct{}{}的区别你知道吗?
首先说下Golang中的结构体,结构体是由一系列具有相同类型或不同类型的数据构成的数据集合,Golang中使用关键字struct来创建一个结构体,语法如下:typeStudentstruct { Name string }下面定义一个Student结构体,例如&am…...
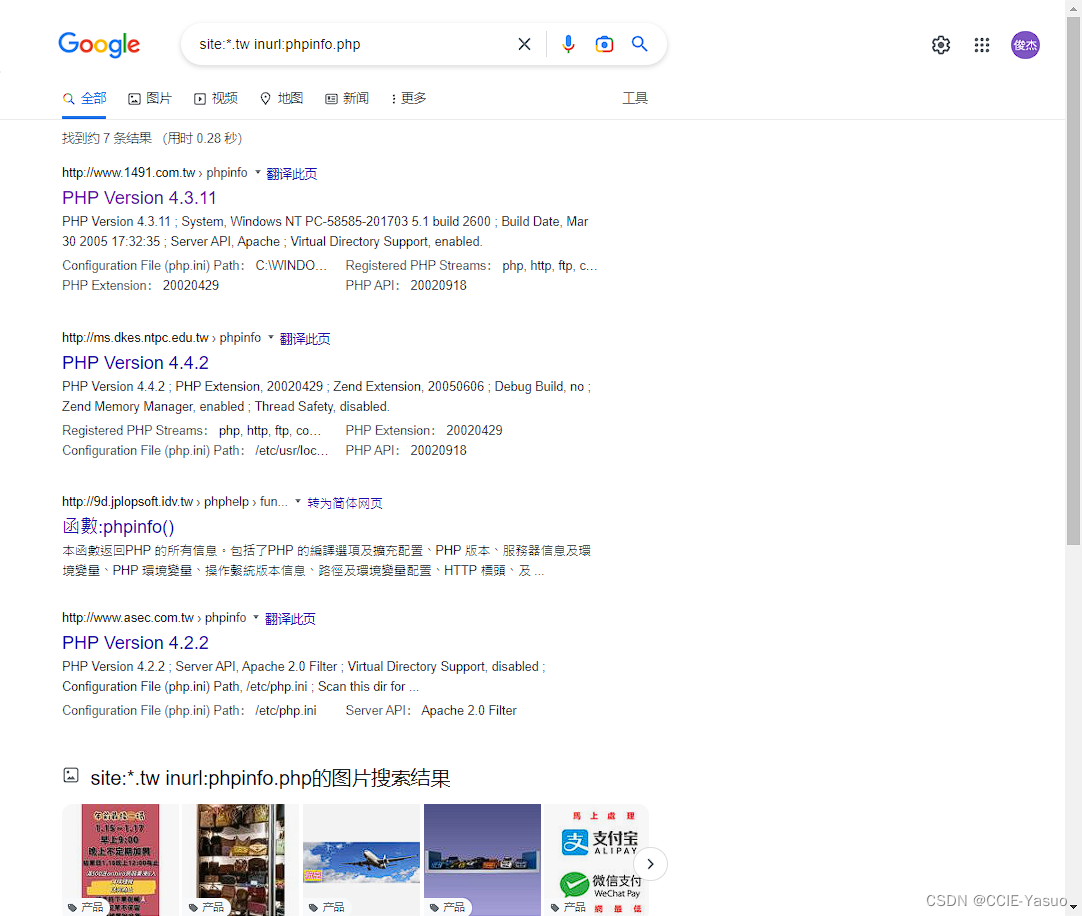
网络安全-信息收集- 谷歌浏览器插件收集信息,谷歌hacking搜索语法-带你玩不一样的搜索引擎
网络安全-信息收集- 谷歌浏览器插件收集信息,谷歌hacking搜索语法-带你玩不一样的搜索引擎 前言 一,我也是初学者记录的笔记 二,可能有错误的地方,请谨慎 三,欢迎各路大神指教 四,任何文章仅作为学习使用 …...

基础篇—一文掌握css的边框属性
CSS 边框属性 CSS边框属性允许你指定一个元素边框的样式和颜色。 1、边框样式 边框样式属性指定要显示什么样的边界。 border-style属性用来定义边框的样式 2、边框宽度 您可以通过 border-width 属性为边框指定宽度。 为边框指定宽度有两种方法:可以指定长度值,比如 2px…...
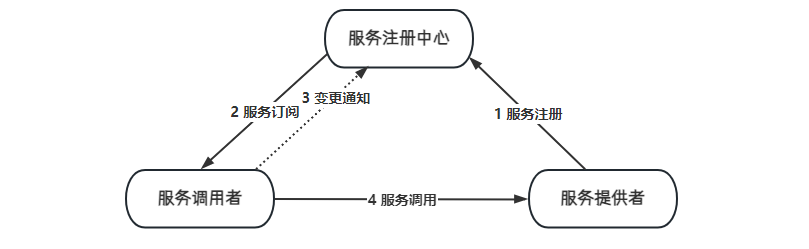
05服务发现:引入etcd服务注册中心
在分布式微服务架构中,服务注册发现组件(通常称为服务注册中心)往往有着举足轻重的作用,它的性能与稳定可能会直接影响到整个服务的状态,比如Spring Cloud中的Eureka、Dubbo中的Zookeeper等等,接下来我们就gRPC微服务中最常见的服务注册中心etcd,来讲述下两者在具体是怎…...

Pdfium.Net SDK 4.78.2704 完美Crack/Ptach
不限制时,/不限PDF体积、、、、、// version: 4.78.2704 | file size: 52.7 Mb Pdfium .Net SDK C# PDF 库 从头开始或从一堆扫描图像创建 PDF 编辑、合并、拆分和操作 PDF,提取文本和图像 嵌入独立的 Winforms 或 WPF PDF 查看器 支持:.Net…...
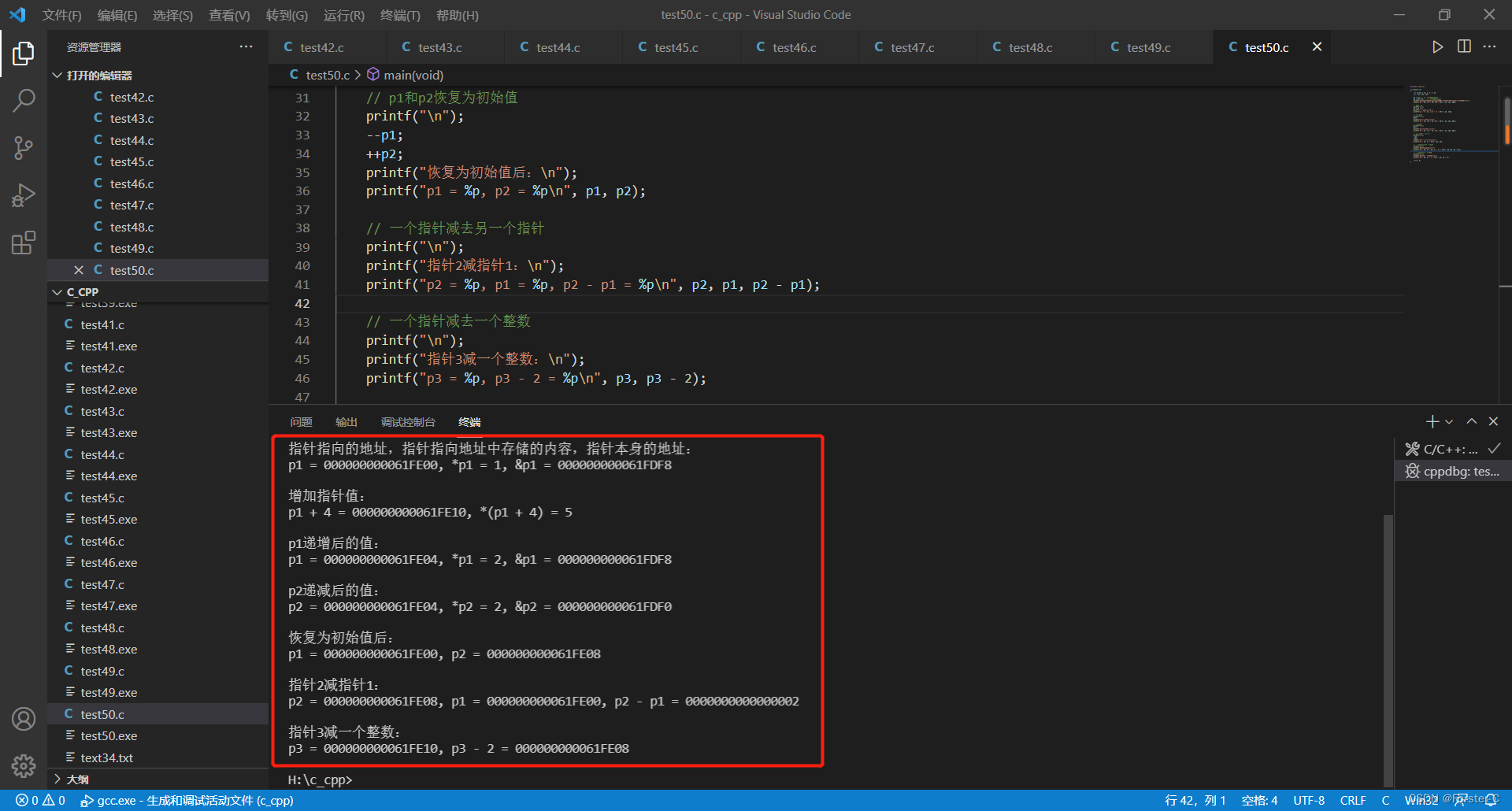
再学C语言38:指针操作
C提供了6种基本的指针操作 示例代码: #include <stdio.h>int main(void) {int arr[5] {1, 2, 3, 4, 5};int * p1, *p2, *p3;p1 arr; // 把一个地址赋给指针p2 &arr[2]; // 把一个地址赋给指针printf("指针指向的地址,指针指向地址中…...
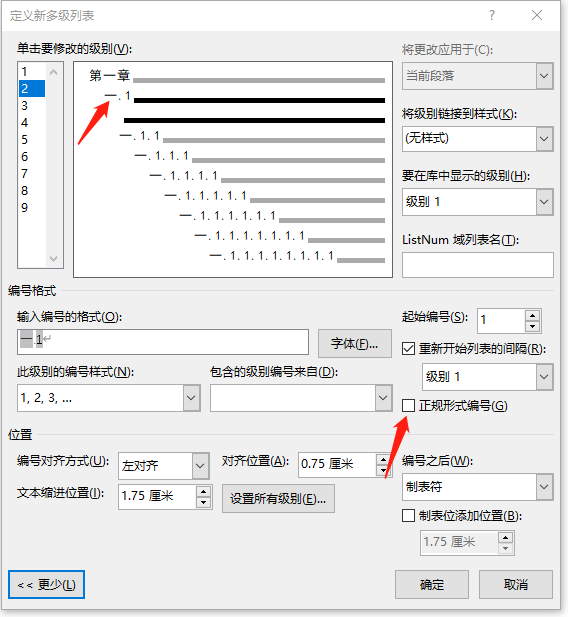
【论文Word排版】使用多级列表设置论文序号
在Word中对论文进行排版 1.设置章节前面的序号 1.1 需求 通常情况下要求如下 一级标题“第一章 XXX”,然后是“1.1 研究意义”, “1.2 研究现状” 之前的处理方式都是手打,并没有借助word的多级列表实现。这次趁着写毕业论文研究了一下。…...
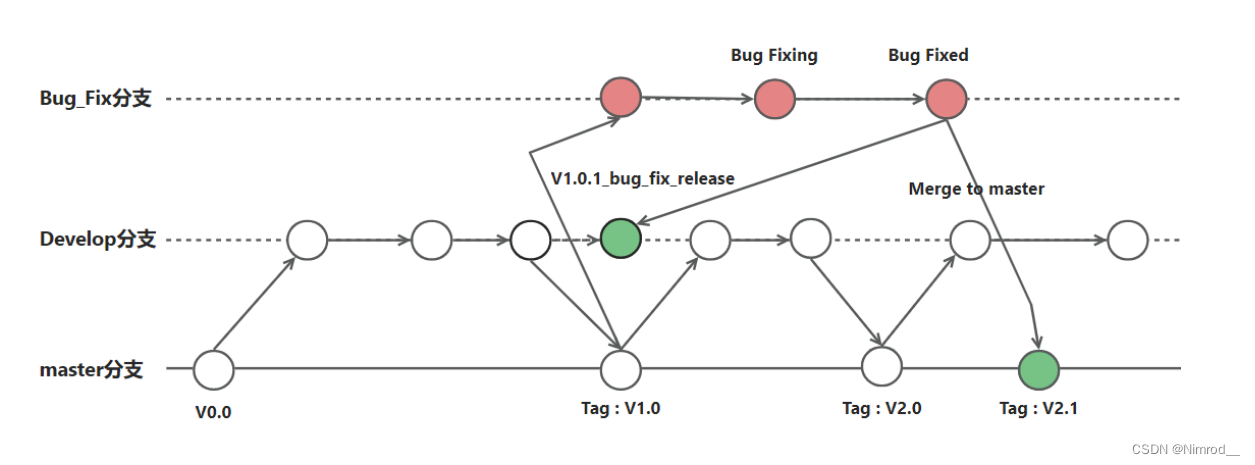
分支管理方案
背景 在工作的过程中,git管理方式已经成为每一个项目开发的基础,每个项目的开发都离不开git管理方式。 但是在使用的过程中,由于对git分支管理方案的了解不深,导致会出现分支管理不明确的情况。 本文主要是做科普作用ÿ…...
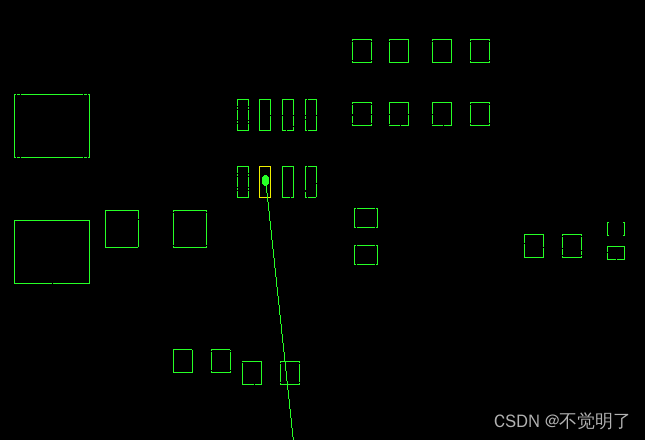
Allegro走线时如何自动关闭其它网络飞线显示操作指导
Allegro走线时如何自动关闭其它网络飞线显示操作指导 在做PCB设计的时候,尤其是在评估布线的时候,走某一个网络的时候,希望其它网络的飞线会被自动关闭,方便评估。 Allegro支持这个功能,如下图 走线前 走线后 具体操作如下 点击Route...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
