22- 隐马尔科夫HMM (NLP自然语言算法) (算法)
HMM模型 :
from hmmlearn.hmm import GaussianHMM
model= GaussianHMM(n_components=3,n_iter=100000, covariance_type = 'diag')
model.fit(X)1、马尔科夫链
有向图模型(贝叶斯网络):用有向图表示变量间的依赖关系;
无向图模型(马尔可夫网):用无向图表示变量间的相关关系。
HMM 就是贝叶斯网络的一种--虽然它的名字里有和"马尔可夫网"一样的马尔可夫。
对变量序列建模的贝叶斯网络又叫动态贝叶斯网络。HMM 就是最简单的动态贝叶斯网络。
注意,马尔可夫过程其原始模型是马尔可夫链。该过程具有如下特性:在已知系统当前状态的条件下,它未来的演变不依赖于过去的演变。
也就是说,一个马尔可夫过程可以表示为系统在状态转移过程中,第 T+1 次结果只受第 T 次结果的影响,即只与当前状态有关,而与过去状态,即与系统的初始状态和此次转移前的所有状态无关。
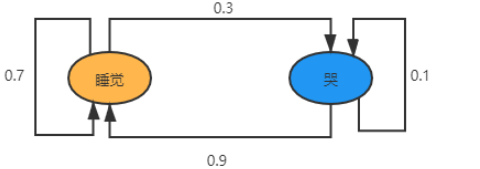
上图就是一个非常简单的马尔可夫链。两个节点分别表示睡和哭。边表示节点之间的转移概率。
睡之后,0.7 的可能又接着睡,只有 0.3 的可能变成哭。而哭之后,0.9 的可能是睡,也就有 0.1 的可能接着哭。
假设这是某个孩子的预报模型(这个孩子就只有哭和睡),则下一个状态只和上一个状态有关。和之前是在哭还是睡的状态没有关系。那么我们只要知道现在的状态,就可以推测接下来是睡还是哭的可能性了。
由马尔科夫链演化而成了隐含马尔可夫模型(Hidden Markov Model, HMM)!
2、HMM概述
2.1、HMM模型介绍
隐马尔科夫模型(Hidden Markov Model,以下简称HMM)是比较经典的机器学习模型了,它在语言识别,自然语言处理,模式识别等领域得到广泛的应用。
当然,随着目前深度学习的崛起,尤其是RNN,LSTM等神经网络序列模型的火热,HMM的地位有所下降。但是作为一个经典的模型,学习HMM的模型和对应算法,对我们解决问题建模的能力提高以及算法思路的拓展还是很好的。
2.2、HMM模型应用
首先我们来看看什么样的问题解决可以用HMM模型。
使用HMM模型时我们的问题一般有这两个特征:
- 我们的问题是基于序列的,比如时间序列,或者状态序列。
- 我们的问题中有两类数据,一类序列数据是可以观测到的,即观测序列;而另一类数据是不能观察到的,即隐藏状态序列,简称状态序列。
有了这两个特征,那么这个问题一般可以用HMM模型来尝试解决。这样的问题在实际生活中是很多的。比如:我现在在打字写博客,我在键盘上敲出来的一系列字符就是观测序列,而我实际想写的一段话就是隐藏序列,输入法的任务就是从敲入的一系列字符尽可能的猜测我要写的一段话,并把最可能的词语放在最前面让我选择,这就可以看做一个HMM模型了。再举一个,我在和你说话,我发出的一串连续的声音就是观测序列,而我实际要表达的一段话就是状态序列,你大脑的任务,就是从这一串连续的声音中判断出我最可能要表达的话的内容。
8、代码演练
8.1、参数估计问题
参数估计问题,也叫学习问题。已知观察序列,来对HMM模型的参数进行估计。
import numpy as np
# pip install hmmlearn
import hmmlearn.hmm as hmm# 首先定义变量
status = ['盒子1', '盒子2', '盒子3'] # 隐藏的状态集合
obs = ['红球', '白球'] # 观察值集合,0==红球,1==白球
n_status = len(status) # 隐藏状态的长度
# 初始概率分布: π 表示初次抽时,抽到1盒子的概率是0.2,抽到2盒子的概率是0.4,抽到3盒子的概率是0.4
pi = np.array([0.2, 0.4, 0.4]) # 状态转移概率矩阵 A[0][0]=0.5 表示当前我抽到1盒子,下次还抽到1盒子的概率是0.5
A = np.array([[0.5, 0.2, 0.3],[0.3, 0.5, 0.2],[0.2, 0.3, 0.5]])
# 观测概率矩阵 B:B[2][0]=0.7,表示第三个盒子抽到红球概率0.7,B[2][1]=0.3,表示第三个盒子抽到白球概率0.3
B = np.array([[0.5, 0.5],[0.4, 0.6],[0.7, 0.3]])
# 下面开始定义模型
'''
hmmlearn中主要有两种模型,分布为:GaussianHMM和MultinomialHMM;
如果观测值是连续的,那么建议使用GaussianHMM,否则使用MultinomialHMM
参数:
初始的隐藏状态概率π参数为: startprob;
状态转移矩阵A参数为: transmat;
状态和观测值之间的转移矩阵B参数为:
emissionprob_(MultinomialHMM模型中)或者在GaussianHMM模型中直接给定均值(means)和方差/协方差矩阵(covars)
'''
model = hmm.MultinomialHMM(n_components=n_status) # 隐藏状态长度
model.startprob_ = pi # 初始概率
model.transmat_ = A # 状态概率矩阵
model.emissionprob_ = B # 观测概率矩阵
# 观测序列[红、白、红]
se = np.array([[0,1,0]]).T# 对数概率,index索引
logprob,box_index = model.decode(se,algorithm = 'viterbi')
print('隐藏状态盒子:')
print(' '.join(map(lambda t:status[t],box_index)))
print('最终计算的概率是:')
print(np.round(np.exp(logprob),4))8.2、参数估计(训练问题)
已知观察序列,求什么样的隐藏状态序列最可能生成一个给定的观察序列
import numpy as np
# pip install hmmlearn
import hmmlearn.hmm as hmm# 首先定义变量
status = ['盒子1', '盒子2', '盒子3'] # 隐藏的状态集合
obs = ['红球', '白球'] # 观察值集合,0==红球,1==白球
n_status = len(status) # 隐藏状态的长度# 观测数据
X_train = np.array([[0,1,0,1,0],# 第一次观测得到结果:红、白、红、白、红[0,0,1,1,0],[1,1,1,1,0],[0,1,1,1,0],[1,0,1,0,1]])# 状态转移矩阵A?观察概率矩阵 B? 初始概率 Pi?
model = hmm.MultinomialHMM(n_components=n_status,n_iter=10,tol = 0.0001,algorithm='viterbi')
model.fit(X_train)# 查看模型估计的参数
# 概率问题,答案不是唯一的
print('初始概率是:',model.startprob_.round(5))
print('状态转移概率A:\n',model.transmat_.round(5))
print('观察概率矩阵B:\n',model.emissionprob_.round(5))8.3、股票走势预测
8.3.1、加载数据
import numpy as np
import pandas as pdfrom hmmlearn.hmm import GaussianHMM # 股票的交易,数据每天都不一样,变化,连续数值
data = pd.read_csv('./apple_stock.csv') # 苹果公司,股票情况
print(data.shape)data.head()3.2 日期转换
data['Date'] = pd.to_datetime(data['Date'],format = '%Y/%m/%d',errors = 'ignore')
data.info()
3.3 数据提取
# 去除第一天的数据
volume = data['Volume'].values[1:] # 去除了交易额第一天的数据close_v = data['Close'].values# 前后两天股价数值的差值
diff = np.diff(close_v) # 涨、跌、平X = np.column_stack([diff,volume])
X.shape3.4 HMM算法建模
model= GaussianHMM(n_components=3,n_iter=100000, covariance_type = 'diag')model.fit(X)for i in range(model.n_components):# 模型的隐含状态:涨跌平print('第{0}个隐含状态'.format(i))print('平均值是:',model.means_[i])print('方差是:',np.diag(model.covars_[i]))print('------------------------------')3.5 状态转移
print(model.transmat_.round(3))
'''
Transition matrix
[[0.898 0. 0.102]
[0. 0.915 0.085]
[0.083 0.043 0.874]]
'''- 第一行最大的数值是0.915,因此跌倾向于保持自己的状态,即第二天仍旧为跌。
- 第二行最大的数值是0.898,得知涨后第二天倾向于变为涨。
- 根据第三行转变状态最大数值0.874,平后第二天仍旧倾向于平。
相关文章:

22- 隐马尔科夫HMM (NLP自然语言算法) (算法)
HMM模型 : from hmmlearn.hmm import GaussianHMM model GaussianHMM(n_components3,n_iter100000, covariance_type diag) model.fit(X) 1、马尔科夫链 有向图模型(贝叶斯网络):用有向图表示变量间的依赖关系; 无向图模型&…...

gRPC是什么,怎么用
RPC是什么 RPC是指远程过程调用,也就是说两台服务器A,B,一个应用部署在A服务器上,想要调用B服务器上应用提供的函数/方法,由于不在一个内存空间,不能直接调用,需要通过网络来表达调用的语义和传…...

linux基本功系列之fdisk命令实战
文章目录前言一. fdisk命令介绍二. 语法格式及常用选项三. 参考案例3.1 列出每个分区的大小3.2 分区操作3.2.1 添加硬盘3.2.2 开启虚拟机并分区3.3.3 分区完成后进行格式化挂载四 . 设置分区自动挂载前言 大家好,又见面了,我是沐风晓月,本文…...
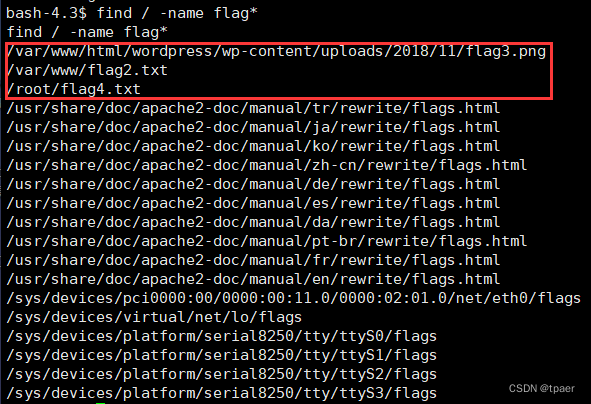
Mysql UDF提权复现Raven2
Raven2通关过程 主要通过Raven2靶机进行复现Mysql UDF提权,以下为通关过程。 靶机镜像:https://www.vulnhub.com/entry/raven-2,269/ 信息收集 拿到靶机ip:192.168.112.129 nmap -sP 192.168.112.0/24探测开放端口,nmap用烂了…...
枚举类(enum)
定义:在某些情况下,一个类的实例对象是有限且固定的,可将该类称为“枚举类”。枚举类是JDK 1.5 之后提出来的。例如:四季只有春夏秋冬4个季节,性别只有男女2个,故四季类和性别类均可称为“枚举类”。 在自…...
腾讯云架构师亲码“redis深度笔记”,从入门到精通,面面俱到
前言 作为这个时代码代码的秃头人员,对Redis肯定是不陌生的,如果连Redis都没用过,还真不好意思出去面试,指不定被面试官吊打多少次。 毕竟现在互联网公司和一些创业公司都要用到Redis,像亚马逊、谷歌、阿里、腾讯都要…...

萌新应该如何开始学习走向自动化测试高薪岗位?
对于测试人员来说,不管进行功能测试还是自动化测试,还是性能测试,都是需要编写测试用例,所以我们必须先要了解清楚手工测试用例与自动化测试用例的一些特点,才能更好的开展自动化测试工作。1.1手工测试用例和自动化测试…...

-bash: pip: command not found
背景 这个错误的原因就是,我们的服务器上没有安装pip,装上就可以了,下面我们看一下centos中的解决方案 下载 wget https://bootstrap.pypa.io/get-pip.py 下载完成后如下图: 安装 安装的时候首先需要看一下自己的python是什…...
使用HTTP隧道代理,请求超过频率要怎么办?
在网上,经常会看到有人说使用隧道代理经常遇到429错误(请求超过频率),我们要如何解决这一问题呢?通常情况,优质的HTTP代理厂商隧道代理服务器采用的是高性能主机构建的动态IP代理服务器,是可以支…...

paddle 49 ODConv的可部署调整
ODConv是一种适用于轻量化模型的conv结构,可以在较少的参数下训练出多参数模型才能达到的精度,在相同的flop下可以稳定的涨2-3%个点。但是在paddle下部署ODConv动态卷积模型时会报出各种异常,导致模型无法转静态图或onnx格式(可能在pytorch下也是无法转换的)。为此研究ODC…...

C++ STL 学习之【string】
✨个人主页: Yohifo 🎉所属专栏: C修行之路 🎊每篇一句: 图片来源 The key is to keep company only with people who uplift you, whose presence calls forth your best. 关键是只与那些提升你的人在一起,…...
使用开源 MaxKey 与 APISIX 网关保护你的 API
1. Apache APISIX介绍 Apache APISIX 是 Apache 软件基金会下的云原生 API 网关,它兼具动态、实时、高性能等特点,提供了负载均衡、动态上游、灰度发布(金丝雀发布)、服务熔断、身份认证、可观测性等丰富的流量管理功能。我们可以…...
Linux之Xshell工具使用
shell简介Xshell是一个远程工具,可以远程连接linux系统 ,SSH,远程管理 Xshell来远程访问Linux系统的终端 。shell的英文含义是“壳”;它是相对于内核来说的,因为它是建立在内核的基础上,面向于用户的一种表…...
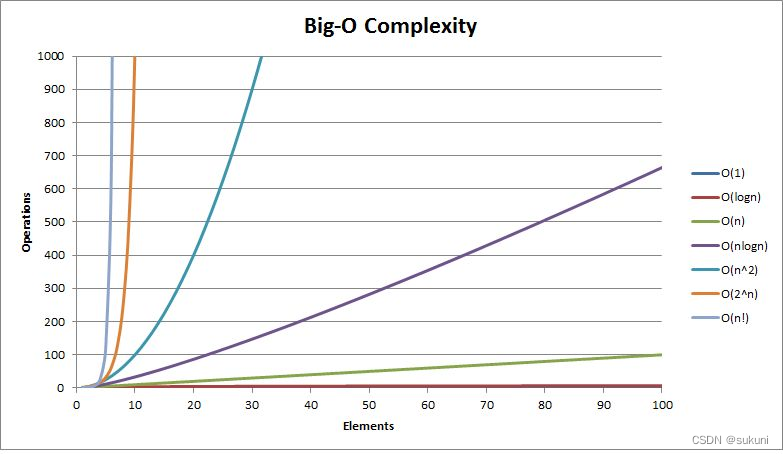
【数据结构与算法】时间复杂度与空间复杂度
目录 一.前言 二.时间复杂度 1.概念 二.大O的渐进表示法 概念: 总结: 三.常见时间复杂度计算举例 例1 例2 例3 例4 例5.计算冒泡排序的时间复杂度 例6.二分算法的时间复杂度 例7.阶乘递归Fac的时间复杂度 例8.斐波那契递归的时间复杂度 …...

Nginx如何配置Http、Https、WS、WSS的方法步骤
这篇文章主要介绍了Nginx如何配置Http、Https、WS、WSS的方法步骤,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友们下面随着小编来一起学习学习吧 写在前面 当今互联网领域,Nginx是使…...

【博客621】iptables -J动作总结
iptables -J动作总结 1、iptables常见动作 ACCEPTDROPREJECTLOGSNATDNATMASQUERADEREDIRECT 2、iptables常见动作用法 2-1、ACCEPT: 作用:用于接收匹配的流量,使得流量继续往后面的规则和链路去匹配 2-2、DROP 作用:用于丢弃匹…...
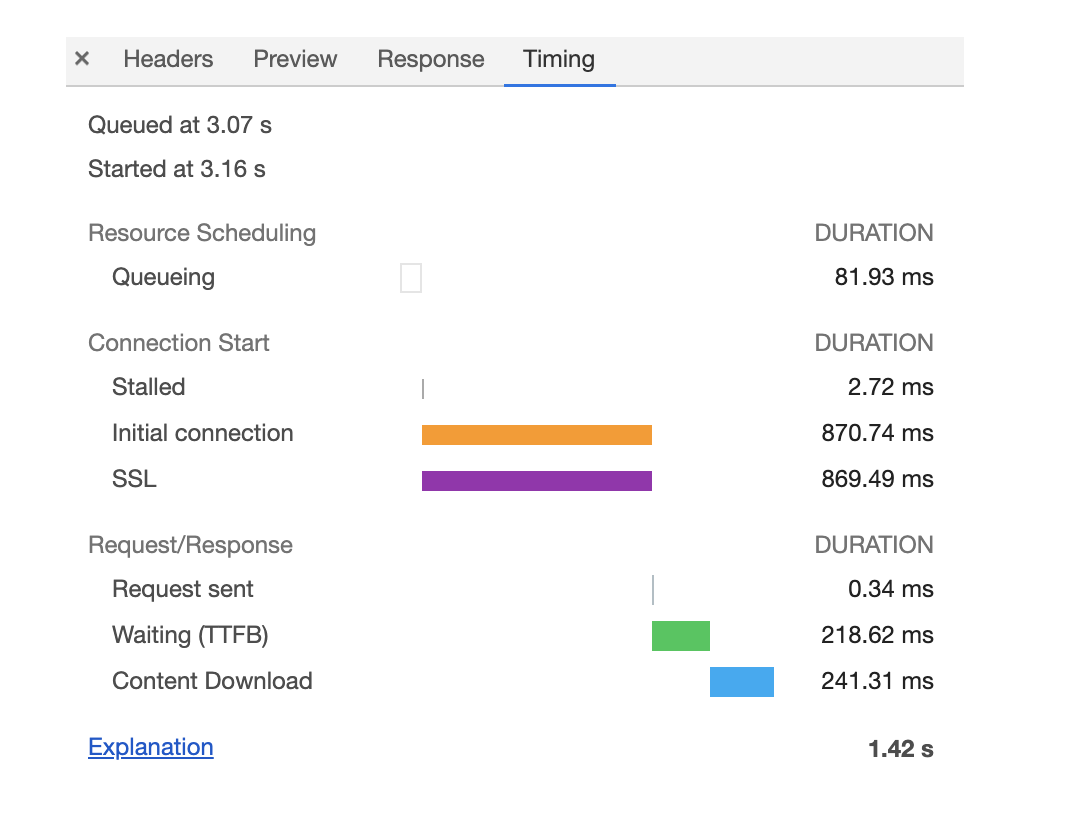
Chrome开发者工具:利用网络面板做性能分析
Chrome 开发者工具(简称 DevTools)是一组网页制作和调试的工具,内嵌于 Google Chrome 浏览器中。 Chrome 开发者工具有很多重要的面板,比如与性能相关的有网络面板、Performance 面板、内存面板等,与调试页面相关的有…...
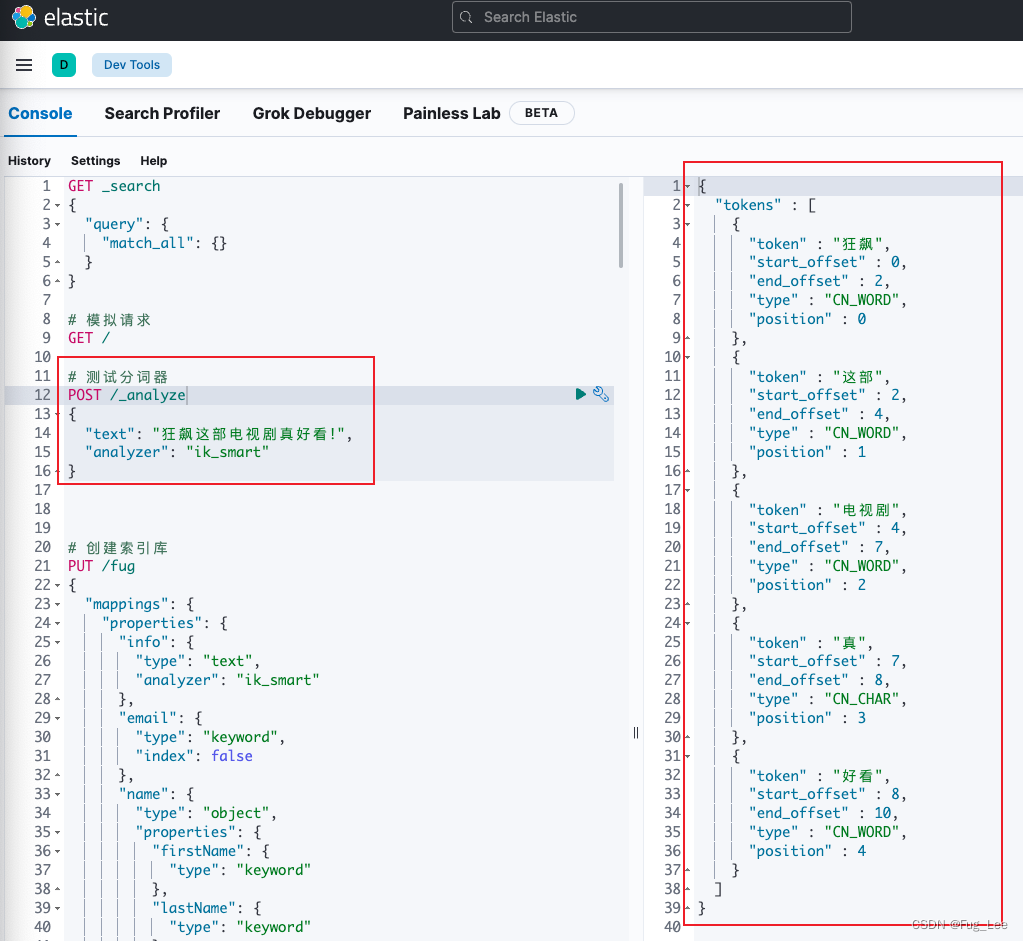
SpringCloud系列(十三)[分布式搜索引擎篇] - ElasticSearch 的概念及 Centos 7 下详细安装步骤
打开淘宝, 搜索 狂飙 会出现各种价格有关狂飙的书籍, 当然也有高启强同款的孙子兵法!!! 如下图所示: 那么面对海量的数据, 如何快速且准确的找到我们想要的内容呢? 淘宝界面已经可以按照综合排序 / 销量 / 信用 / 价格等进行筛选, 是如何做到的呢? ElasticSearch 11 Elastic…...

04_Docker 镜像和仓库
04_Docker 镜像和仓库 文章目录04_Docker 镜像和仓库4.1 什么是 Docker 镜像4.2 列出 Docker 镜像4.3 拉取镜像4.4 查找镜像4.5 构建镜像4.5.1 创建 Docker Hub 账号4.5.2 用 Docker 的 commit 命令创建镜像4.5.3 用 Dockerfile 构建镜像4.5.5 基于 Dockerfile 构建新镜像4.5.5…...
postman-enterprise-API
Postman 是一个用于构建和使用 API 的 API 平台。Postman 简化了 API 生命周期的每个步骤并简化了协作,因此您可以更快地创建更好的 API。 API存储库 在一个中央平台上围绕您的所有 API 工件轻松存储、编目和协作。Postman 可以存储和管理 API 规范、文档、工作流配…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...
