【Python】scipy稀疏矩阵的奇异值分解svds
文章目录
- 基本原理
- scipy实现
- 测试
基本原理
当AAA是方阵时,可以很容易地进行特征分解:A=WΣW−1A=W\Sigma W^{-1}A=WΣW−1,其中Σ\SigmaΣ是AAA的特征值组成的对角矩阵。如果WWW由标准正交基组成,则W−1=WTW^{-1}=W^TW−1=WT,特征分解可进一步写成WTΣWW^T\Sigma WWTΣW。
然而,当AAA不是方阵时,情况大不一样了,但仍然可以将AAA表示成A=UΣVTA=U\Sigma V^TA=UΣVT的形式,其中Σ\SigmaΣ也是对角矩阵,对角线上的每个元素被称作奇异值。
奇异值的求解过程和特征值息息相关,因为把AAA变成方阵很简单,只要乘以转置就行。故令L=AATL=AA^TL=AAT,R=ATAR=A^TAR=ATA,则L,RL, RL,R都可以求特征值λi\lambda_iλi和特征向量,其中LLL的特征向量为AAA的左奇异向量,RRR的特征向量为右奇异向量。对应的奇异值σi=λi\sigma_i=\sqrt{\lambda_i}σi=λi。
scipy实现
scipy.sparse.linalg中实现了稀疏矩阵奇异值分解算法,其参数列表如下
svds(A, k=6, ncv=None, tol=0, which='LM', v0=None, maxiter=None, return_singular_vectors=True, solver='arpack', random_state=None, options=None)
各参数含义如下
A待分解矩阵k奇异值个数,必须在[k,kmax][k, k_{\max}][k,kmax]之间, 当solver='propack'时,kmax=min(M,N)k_{max}=\min(M,N)kmax=min(M,N),否则kmax=min(M,N)−1k_{max}=\min(M,N)-1kmax=min(M,N)−1ncvsolver='arpack'时,此为Lanczos向量个数,否则此项忽略。tol奇异值容忍度,为0表示达到机器的精度which为'LM'时,选取最大的奇异值;'SM'则选取最小奇异值v0迭代初值maxiter迭代次数return_singular_vectors可选4个值True返回奇异向量False不返回奇异向量"u": 如果M <= N,只计算左奇异向量"vh": 如果M > N,只计算右奇异向量;如果solver='propack',这个选项将忽略矩阵维度
solver可选'arpack','propack','lobpcg',但比较吊诡的是,似乎并没有关于这三者区别的文档random_state设置随机数状态optionsdict求解器参数
其返回值有三
- u 即UUU
- s 即奇异值数组,也就是Σ\SigmaΣ的对角线
- vh 即VTV^TVT
测试
下面对奇异值分解做个测试
import numpy as np
from scipy.linalg import svd
from scipy.sparse import csc_array
from scipy.sparse.linalg import svds
np.random.seed(42) # 设置随机数状态
mat = np.random.rand(500,800)
mat[mat<0.9] = 0
csc = csc_array(mat)
u1, s1, vh1 = svds(csc, k=10)
u2, s2, vh2 = svd(mat)
结果是svds得到的结果和svd的前十个值完全相同,只是排序不一样,但也无关紧要。
下面测试一下二者的时间,由于在Windows下用不了propack,所以svds计算的奇异值数最多只能是M−1M-1M−1,也就是499,所以只能测试这个和svd返回500个奇异值的结果相比对,结果如下
>>> from timeit import timeit
>>> timeit(lambda : svds(csc, k=499), number=10)
3.651770199999987
>>> timeit(lambda : svd(mat), number=10)
0.47201400000005833
可见,稀疏矩阵在计算上的确是比不上规整的矩阵。
相关文章:

【Python】scipy稀疏矩阵的奇异值分解svds
文章目录基本原理scipy实现测试基本原理 当AAA是方阵时,可以很容易地进行特征分解:AWΣW−1AW\Sigma W^{-1}AWΣW−1,其中Σ\SigmaΣ是AAA的特征值组成的对角矩阵。如果WWW由标准正交基组成,则W−1WTW^{-1}W^TW−1WT,…...

网络安全等级保护基础知识汇总
等保 全称是网络安全等级保护,分为两个阶段 等保1.0 1994年国务院147令《中华人民共和国计算机信息系统安全保护条例》 等保2.0 2017年 网络安全法,21条规定的 国家实行网络安全等级保护制度,等保进入了有法可依阶段。 2019年国标22239-2019版…...

ros1使用过程中遇到的问题记录
Failed to fetch current robot state如果使用的是moveit助手生成的demo.launch文件启动机械臂的话,应该是其他在运行的自己写的节点代码中少了spin函数,因为getCurrentPose函数依赖于spin,也可以使用AsyncSpinner。具体看下面这个链接https:…...
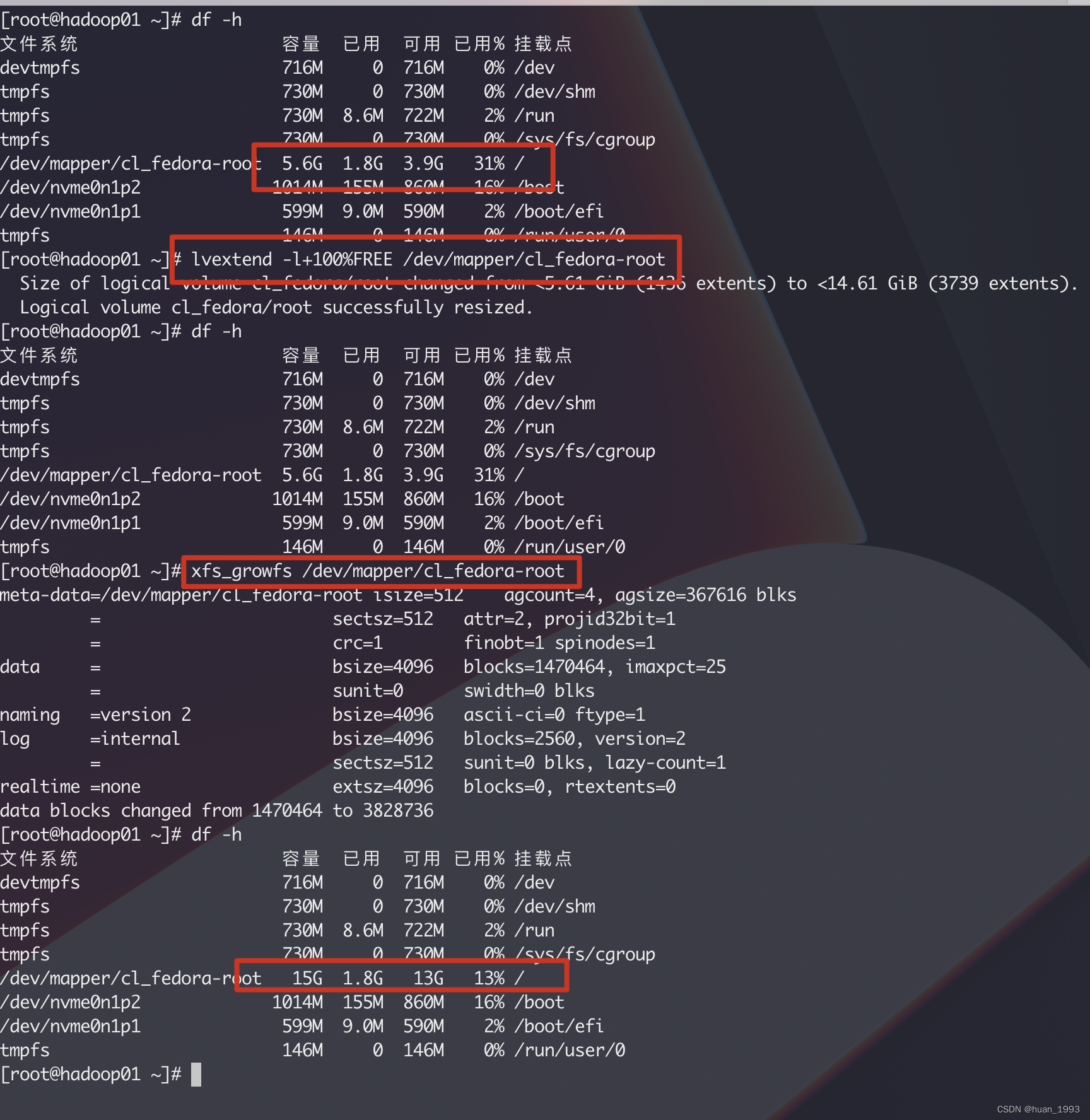
centos7给已有分区进行扩容
1、背景 最近我在虚拟机上安装软件,发现磁盘空间不足,通过上网查找资料,发现可以通过如下方法进行磁盘扩容,此处进行记录一下。 2、实现扩容 1、虚拟机上添加一个新的硬盘 2、查看我们刚刚加入的硬盘 此处我们可以看到/dev/nvm…...

package.json
{"name": "project-name", 项目名字"version": "0.1.0", 版本号"private": true, 项目包,不需要发版"scripts": { 脚本"serve": "vue-cli-service serve", 运行命令后缀是 se…...
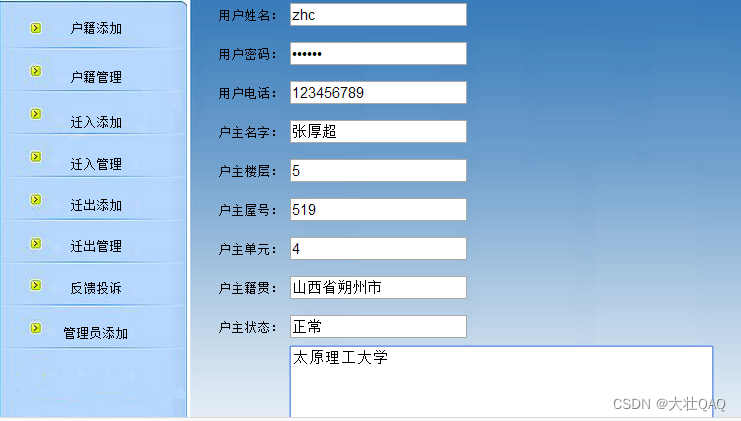
【项目精选】户籍管理系统(视频+论文+源码)
点击下载源码 当今社会人们生活质量越来越高,人们对生活品质的追求不断提升,对于孩子求学,变更住所等情况时有发生,因此对于户籍变动管理就显得十分重要,管理用户的户籍信息可以有效防止信息错乱,信息管理过…...

【IP技术】网络安全防护措施
网络安全威胁造成的形式主要包含运用系统软件缺点或侧门,运用网络防火墙安全隐患,内部结构客户的泄密、泄露和毁坏,动态口令进攻和拒绝服务式攻击等。针对该网络安全威胁,现阶段的预防措施主要有五种:1.访问控制技术&a…...
)
基于AIOT技术的智慧教室智能物联管控系统设计与实现(提纲)
摘要随着物联网技术的不断发展和智能化的不断推进,智慧教室已经成为现代教育中不可或缺的一部分。本文提出了一种基于AIOT技术的智慧教室智能物联管控系统设计与实现方案,该方案集成了物联网技术、人工智能技术、大数据技术和云计算技术等先进技术&#…...

C 指针的深造
C 指针1 关于内存那点事2 指针的概念3 指针变量的定义方法4 指针的分类5 指针和变量的关系6 指针和数组元素之间的关系7 指针数组8 指针的指针9 字符串和指针9.1 字符串的定义9.2 字符串的可修改性:9.3 初始化赋值9.4 使用时赋值9.5 字符串和指针总结10 数组指针11 …...
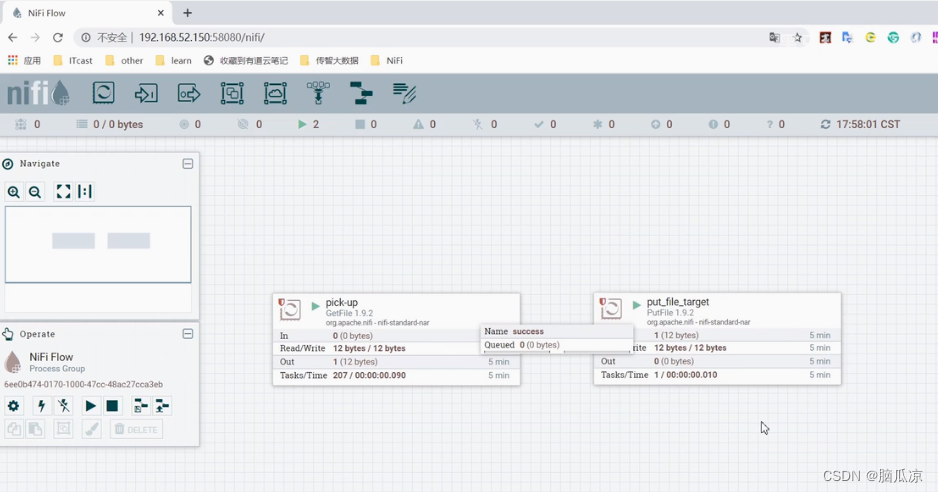
大数据之-Nifi-应用场景2-2_设置putfile处理器自动创建目标文件夹_以及存在重复文件时自动覆盖---大数据之Nifi工作笔记0006
上一节我们留了两个问题,一个是,如果我们没有创建putfile要写入的目标文件夹,会报错吗? 可以看到我们putfile目标文件夹是上面这个目录 我们来试一试,如果目标文件夹不存在,putfile处理器会自动创建吗 首先我们删除这个target目标文件夹 然后我们进入cd source目录,源文件夹目…...

buuctf Web 下
9.[ACTF2020 新生赛]Exec 访问url: http://cc3c6c27-e2df-4665-baba-1d9a32dc963e.node3.buuoj.cn/ 首页如下: 直接ping ip可以得到结果 常见管道符 1、|(就是按位或),直接执行|后面的语句 127.0.0.1 | cat /flag…...
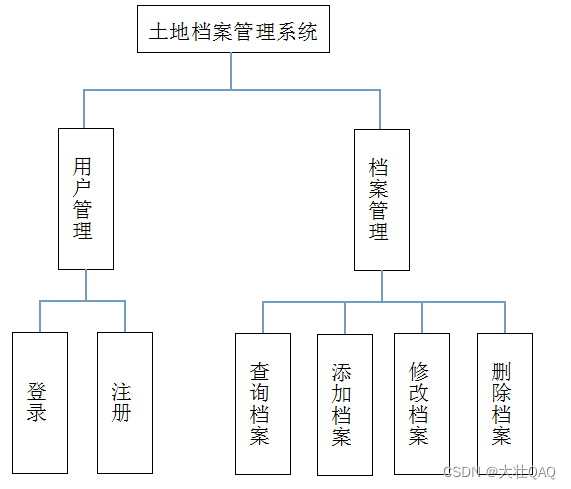
【项目精选】javaEE土地档案管理系统(源码+论文+视频)
技术:java、jsp、struts、spring、hibernate 数据库:oracle 集成开发工具:eclipse 点击下载源码 本土地项目管理系统在可行性研究的基础上,是为了进一步明确土地项目管理系统的软件需求,以便安排项目规划和进度&#x…...

JVM那些事——垃圾回收和内存分配
内存分配 默认情况下新生代和老年区的内存比例是1:2,新生代中Eden区和Survivor区的比例是8:1。 对象优先分配在Eden区。大对象直接进入老年区。通过-XX:PertenureizeThreshold参数设置临界值。长期存活的对象进入老年区。对象每熬过一次Minor GC,年龄1&…...

什么牌的运动耳机比较好、运动耳机排行榜10强
现在运动健身的潮流持续不下,而且人们长期坐于办公室办公,严重影响身体的健康,这时不论是去健身房锻炼,还是户外跑步都是非常必要的了,而蓝牙耳机作为运动必备的一款数码产品,更是受到了大家的青睐…...
)
华为OD机试题 - N 进制减法(JavaScript)
最近更新的博客 2023新华为OD机试题 - 斗地主(JavaScript)2023新华为OD机试题 - 箱子之形摆放(JavaScript)2023新华为OD机试题 - 考古学家(JavaScript)2023新华为OD机试题 - 相同数字的积木游戏 1(JavaScript)2023新华为OD机试题 - 最多等和不相交连续子序列(JavaScri…...

MyBatis 之三(查询操作 占位符#{} 与 ${}、like查询、resultMap、association、collection)
文章目录1. 参数占位符 #{} 和 ${} 的区别2. ${} 的优点3. SQL 注入问题4. like 查询5. 返回字典映射:resultMap6. 一对一查询:association7. 一对多查询:collection回顾一下,在上一篇 MyBatis 之二(增、删、改操作&am…...

【云原生之Docker实战】使用Docker部署Web在线聊天室Rocket.Chat
【云原生之Docker实战】使用Docker部署Web在线聊天室Rocket.Chat 一、Rocket.Chat介绍二、检查本地系统环境1.检查系统版本2.检查docker版本3.检查docker状态4.检查docker compose版本三、下载Rocket.Chat镜像四、部署Rocket.Chat1.创建部署目录2.编辑docker-compose.yaml文件3…...
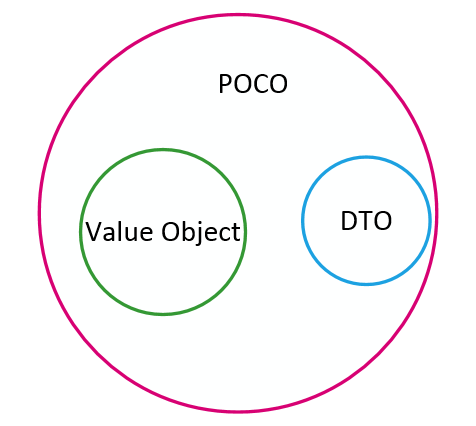
阿里一面:谈一下你对DDD的理解?2W字,帮你实现DDD自由
说在前面 在微服务的应用开发中,DDD 用得越来越普及。 在40岁老架构师 尼恩的读者交流群(50)中,DDD是一个非常、非常高频的交流话题。 最近,有小伙伴面试阿里时,遇到一个面试题: 谈谈你对DDD的理解? 小伙…...

嵌入式Linux入门级板卡的神经网络框架ncnn移植与测试-米尔i.MX6UL开发板
本篇测评由电子发烧友的优秀测评者“ALSET”提供。 米尔 MYD-Y6ULX-V2 开发板,基于 NXP i.MX6UL/i.MX6UL L处理器,该开发板被米尔称之为经典王牌产品。本次测试目标是在此开发板上进行神经网络框架ncnn的移植与测试开发,测试ncnn在此开发板上…...

扬帆优配|杠杆资金重仓股曝光,3只科创板股获多路资金青睐
到2月16日,科创板融资余额环比前一日削减1104.16万元,其间,23股融资余额环比添加超千万元,融资净买入居前的有晶科动力、诺诚健华、爱博医疗等。 到2月16日,市场融资余额算计1.48万亿元,较前一交易日削减27…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...
