BZOJ4403 序列统计
题目描述
给定三个正整数N、L和R,统计长度在1到N之间,元素大小都在L到R之间的单调不降序列的数量。输出答案对106+310^6+3106+3取模的结果。
输入
输入第一行包含一个整数T,表示数据组数。
第2到第T+1行每行包含三个整数N、L和R,N、L和R的意义如题所述。
1≤N,L,R≤10^9,1≤T≤100,输入数据保证L≤R。
输出
输出包含T行,每行有一个数字,表示你所求出的答案对106+310^6+3106+3取模的结果。
样例输入
2
1 4 5
2 4 5
样例输出
2
5
题解
前置知识:lucas定理
在区间[l,r][l,r][l,r]中长度为nnn的单调不降序列的数量,即Cr−l+1+n−1n=Cr−l+nnC_{r-l+1+n-1}^n=C_{r-l+n}^nCr−l+1+n−1n=Cr−l+nn个。
题意即求∑i=1nCr−l+ii\sum\limits_{i=1}^nC_{r-l+i}^ii=1∑nCr−l+ii。因为Cnm=Cnn−mC_n^m=C_n^{n-m}Cnm=Cnn−m,所以
∑i=1nCr−l+ii=∑i=1nCr−l+ir−l\sum\limits_{i=1}^nC_{r-l+i}^i=\sum\limits_{i=1}^nC_{r-l+i}^{r-l}i=1∑nCr−l+ii=i=1∑nCr−l+ir−l
又因为
∑i=mnCim=Cn+1m+1\sum\limits_{i=m}^nC_i^m=C_{n+1}^{m+1}i=m∑nCim=Cn+1m+1
所以
∑i=1nCr−l+ir−l=(∑i=0nCr−l+ir−l)−1=Cr−l+n+1r−l+1−1=Cr−l+n+1n−1\sum\limits_{i=1}^nC_{r-l+i}^{r-l}=(\sum\limits_{i=0}^nC_{r-l+i}^{r-l})-1=C_{r-l+n+1}^{r-l+1}-1=C_{r-l+n+1}^n-1i=1∑nCr−l+ir−l=(i=0∑nCr−l+ir−l)−1=Cr−l+n+1r−l+1−1=Cr−l+n+1n−1
Cr−l+n+1n−1C_{r-l+n+1}^n-1Cr−l+n+1n−1即为答案,用lucas定理求出即可。
code
#include<bits/stdc++.h>
using namespace std;
int n;
long long vt=1,x,y,ans=0,a[15],b[15];
void exgcd(long long c,long long d){if(d==0){x=1;y=0;return;}exgcd(d,c%d);long long t=x;x=y;y=t-c/d*y;
}
int main()
{scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%lld%lld",&a[i],&b[i]);vt=vt*a[i];}for(int i=1;i<=n;i++){exgcd(vt/a[i],a[i]);x=(x%a[i]+a[i])%a[i];ans=(ans+vt/a[i]*b[i]*x%vt)%vt;}printf("%lld",ans);return 0;
}
相关文章:

BZOJ4403 序列统计
题目描述 给定三个正整数N、L和R,统计长度在1到N之间,元素大小都在L到R之间的单调不降序列的数量。输出答案对106310^631063取模的结果。 输入 输入第一行包含一个整数T,表示数据组数。 第2到第T1行每行包含三个整数N、L和R,N、…...
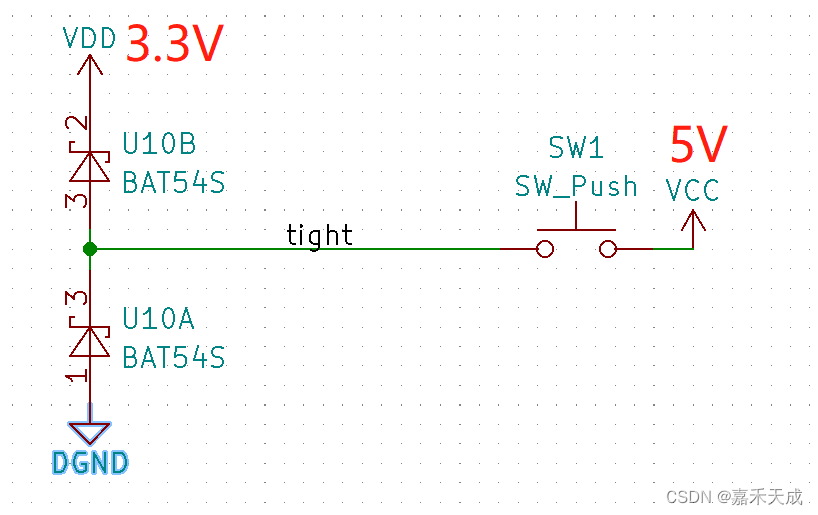
如何正确使用 钳位二极管
在电路设计中,经常遇到需要IO保护的场景,比如ADC采样,GPIO接收电平信号等。 常见的保护方法有分压,限幅,限流等。本次我们讨论限幅方法中的 钳位二极管。 我们以BAT54S为例,它的符号是这样的, 而在很多手册里,我们可以看到,一般是这样使用的: 因此,我设计了简化…...
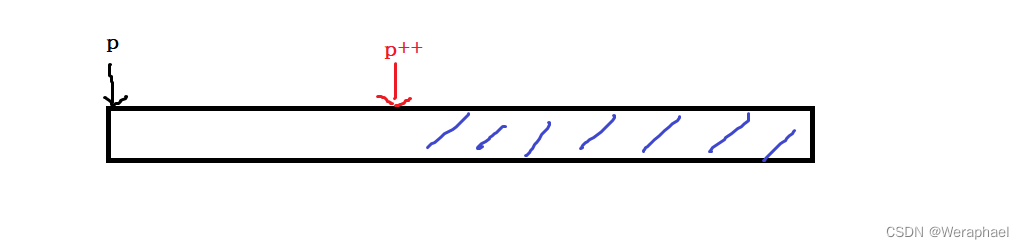
【C语言进阶】动态内存管理
👦个人主页:Weraphael ✍🏻作者简介:目前是C语言学习者 ✈️专栏:C语言航路 🐋 希望大家多多支持,咱一起进步!😁 如果文章对你有帮助的话 欢迎 评论💬 点赞&a…...

第一批因ChatGPT坐牢的人,已经上路了
大家好,我是 Jack。 ChatGPT 的火爆有目共睹,有人靠着它赚了第一桶金,也有人靠着它即将吃上第一顿牢饭。 任何一件东西的火爆,总会给一些聪明人带来机会。 艾尔登法环火的时候,一堆淘宝卖魂的;羊了个羊火…...

Eclipse下Maven的集成
Eclipse下Maven的集成 2.1指定本地maven环境 参考:Eclipse的Maven创建_叶书文的博客-CSDN博客_eclipse创建maven项目 指定用本地maven指定maven仓库设置和地址2.2创建maven项目 1.新建 2.目录设置 3.坐标设置(随便写就行) 4.目录结构 2.3配置…...

Elasticsearch7学习笔记(尚硅谷)
文章目录一、ElasticSearch概述1、ElasticSearch是什么2、全文搜索引擎3、ElasticSearch 和 Solr3.1 概述3.2 比较总结二、Elasticsearch入门1、Elasticsearch安装1.1 下载使用1.2 数据格式2、索引操作3、文档操作(了解)3.1 创建文档3.2 文档查询3.3 文档…...

前端学习第一阶段-第7章 品优购电商项目
7-1 品优购项目介绍及准备工作 01-品优购项目导读 02-网站制作流程 03-品优购项目规划 04-品优购项目搭建 05-品优购项目-样式的模块化开发 06-品优购项目-favicon图标制作 07-品优购项目-TDK三大标签SEO优化 7-2 首页Header区域实现 08-品优购首页-快捷导航shortcut结构搭建 0…...

cocos2dx 4.0 - cpp - pc版 环境搭建
开发环境vs2022 cocos2dx4.0 python2.7.18 cmake3.25安装教程(环境搭建)安装VS2022-Community, 勾选c进行安装安装cmake3.25, 勾选环境变量进行安装安装python2.7.18, 勾选环境变量进行安装下载cocos2dx4.0并解压配置cocos2dx:运行cmd,进入…...
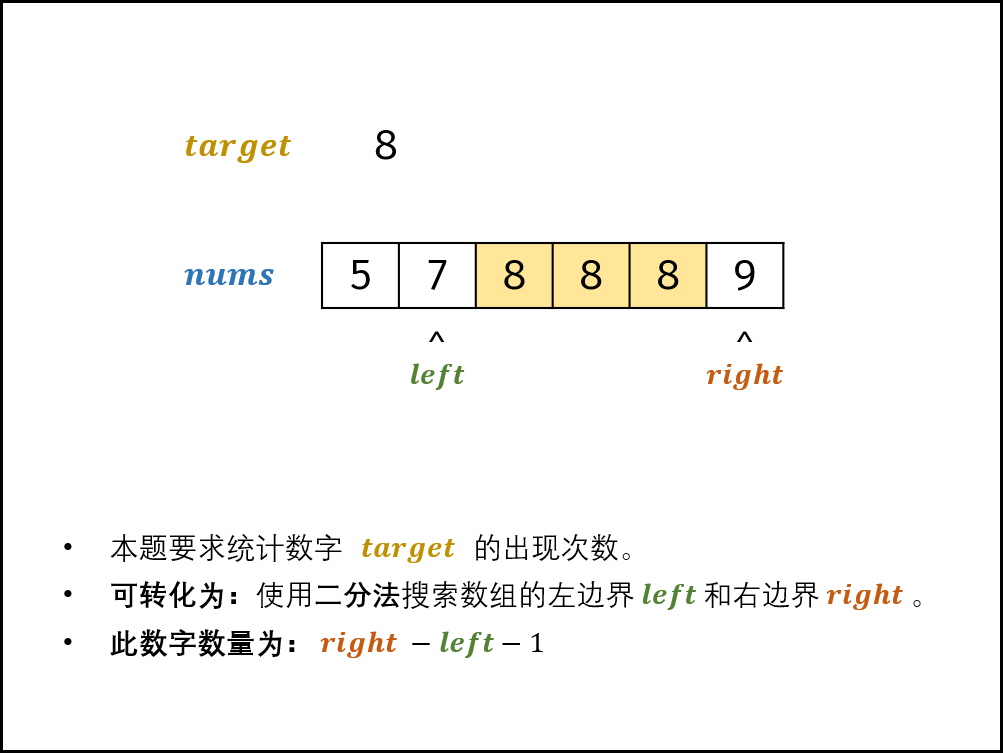
剑指 Offer 53 - I. 在排序数组中查找数字 I
原题链接 难度:easy\color{Green}{easy}easy 题目描述 统计一个数字在排序数组中出现的次数。 示例 1: 输入: nums [5,7,7,8,8,10], target 8 输出: 2示例 2: 输入: nums [5,7,7,8,8,10], target 6 输出: 0提示: 0<nums.length<1050 <…...
 | 机试题算法思路 【2023】)
华为OD机试 - 删除指定目录(Python) | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 热点网络统计 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 查找单入口空闲区域 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 好朋友 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 找出同班小朋友 | 备考思路,刷题要点…...

PowerShell Install Office 2021 Pro Plus Viso Professional
前言 微软Office在很长一段时间内都是最常用和最受欢迎的软件。从小型创业公司到大公司,它的使用比例相当。它可以很容易地从微软的官方网站下载。但是,微软只提供安装程序,而不提供完整的软件供下载。这些安装文件通常比较小。下载并运行后,安装的文件将从后端服务器安装M…...

KubeSphere实战
文章目录一、KubeSphere平台安装1、Kubernetes上安装KubeSphere1.1 安装docker1.2 安装Kubernetes1.3 前置环境之nfs存储1.4 前置环境之metrics-server1.5 安装KubeSphere2、Linux单节点部署KubeSphere3、Linux多节点部署KubeSphere(推荐)二、KubeSphere实战1、多租户实战2、中…...

Linux 简介
Linux 内核最初只是由芬兰人林纳斯托瓦兹(Linus Torvalds)在赫尔辛基大学上学时出于个人爱好而编写的。 Linux 是一套免费使用和自由传播的类 Unix 操作系统,是一个基于 POSIX 和 UNIX 的多用户、多任务、支持多线程和多 CPU 的操作系统。 …...
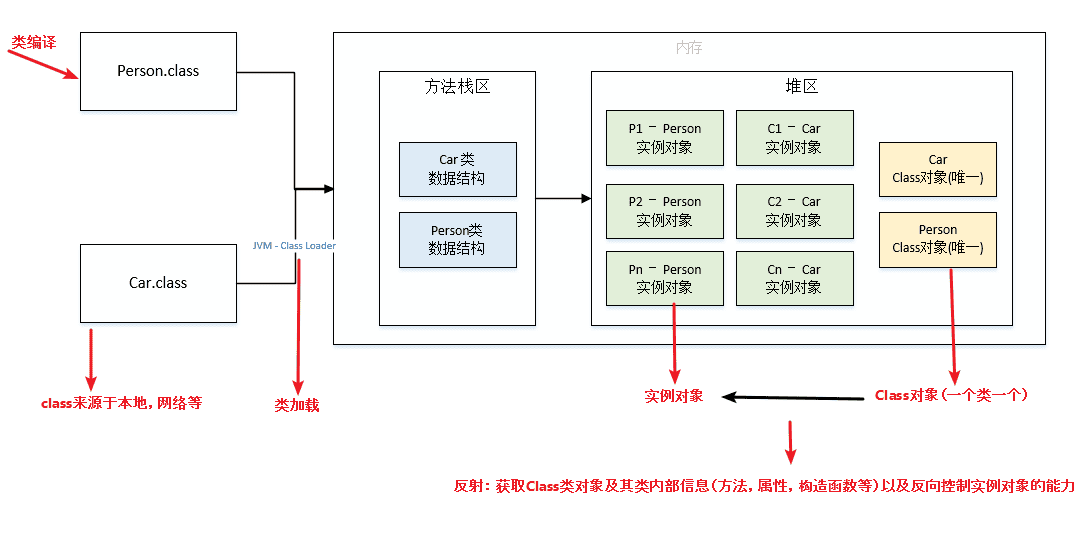
java面试题-泛型异常反射
泛型1.什么是泛型?Java是一种强类型语言,数据类型在编译时必须确定。如果我们想要在代码中使用不同类型的数据,那么就需要为每种类型分别写出相应的代码。这样会导致代码冗长、重复,也不便于维护。为了解决这个问题,Ja…...

详细解读ChatGPT:如何调用ChatGPT的API接口到官方例子的说明以及GitHub上的源码应用和csdn集成的ChatGPT
文章目录1. 解读ChatGPT1.1 词语解释1.2 功能解读2. GitHub上ChatGPT的应用源码3. 调用ChatGPT的API4. 官方例子说明5. 集成ChatGPT自ChatGPT出来到如今,始终走在火热的道路上,如今日活用户破亿,他为何有如此大的魅力,深受广大用户…...

九龙证券|最新评级情况出炉,机构扎堆这一板块!聚氨酯龙头获得最多关注
本周算计254家上市公司获组织“买入型”评级。 电子板块评级组织扎堆 证券时报数据宝计算,2月13日至17日,A股市场53家组织算计进行347次评级,254家上市公司获“买入型”评级(包含买入、增持、强烈推荐、推荐)。 从申…...
考研复试机试 | C++ | 尽量不要用python,很多学校不支持
目录1.1打印日期 (清华大学上机题)题目:代码:1.2改一改:上一题反过来问题代码:2.Day of Week (上交&&清华机试题)题目:代码:3.剩下的树(清…...

ChatGPT时代,别再折腾孩子了
今天这篇完全是从两件事儿有感而发。昨天在文印店,在复印机上看到装订好的几页纸,我瞥了一眼,是历史知识点:隋朝大运河分为四段,分别是___ ___ ___ ___,连接了五大河___ ___ ___ ___ ______ 年ÿ…...

万字干货 | 荔枝魔方基于云原生的架构设计与实践
近年来,荔枝集团在国内和海外的业务迅速发展,业务数据规模也是成几何式地增长,海量数据的计算分析场景、业务智能算法应用需求随之而生,为了快速地满足业务发展的需要,我们面临着诸多的技术挑战。技术挑战工程问题资源…...

#科研筑基# python初学自用笔记 第九篇 面向对象编程
面向对象编程 Object Oriented Programming ,简称OOP,是一种程序设计思想,这种思想把对象作为程序的基本单元。类是抽象的,对象是具体的,一种类包括其特定的数据或属性,以及操作数据的函数(方法…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
