【搜索】DFS剪枝与优化
算法提高课笔记
目录
- 小猫爬山
- 题意
- 思路
- 代码
- 数独
- 题意
- 思路
- 代码
- 木棒
- 题意
- 思路
- 代码
- 生日蛋糕
- 题意
- 思路
- 代码
剪枝是什么意思呢?
我们知道,不管是内部搜索还是外部搜索,都可以形成一棵搜索树,如果将搜索树全部遍历一遍,效率会很低,但如果我们能在搜索的过程中,提前预知,判断某一些不可能是正确答案的情况,就可以不用遍历其下的子树,从而提高我们的算法效率
我们可以从以下几个角度考虑剪枝:
- 优化搜索顺序
优先选择分支较少的结点 - 排除等效冗余
尽量保证不搜索重复的状态(就是在不考虑顺序时,采用组合的方式搜索) - 可行性剪枝
不合法提前退出 - 最优性剪枝
如果当前答案无论如何都比目前的最优解要差,那就可以不要往下搜了 - 记忆化搜索(DP)
接下来将通过例题来讲解
小猫爬山
原题链接
翰翰和达达饲养了 N 只小猫,这天,小猫们要去爬山。
经历了千辛万苦,小猫们终于爬上了山顶,但是疲倦的它们再也不想徒步走下山了(呜咕>_<)。
翰翰和达达只好花钱让它们坐索道下山。
索道上的缆车最大承重量为 W,而 N 只小猫的重量分别是 C1、C2……CN。
当然,每辆缆车上的小猫的重量之和不能超过 W。
每租用一辆缆车,翰翰和达达就要付 1 美元,所以他们想知道,最少需要付多少美元才能把这 N 只小猫都运送下山?
输入格式
第 1 行:包含两个用空格隔开的整数,N 和 W。
第 2…N+1 行:每行一个整数,其中第 i+1 行的整数表示第 i 只小猫的重量 Ci。
输出格式
输出一个整数,表示最少需要多少美元,也就是最少需要多少辆缆车。
数据范围
1 ≤ N ≤ 18,
1 ≤ Ci ≤ W ≤ 108
输入样例
5 1996
1
2
1994
12
29
输出样例
2
题意
给出小猫重量、缆车承重,问最少要多少缆车能把所有小猫运走
思路
枚举每只小猫,有两种状态:
- 放到当前这辆车上
- 新开一辆车
优化:
- 优化搜索顺序:比较一只比较轻的猫和另一只比较重的猫,显然是比较重的猫带来的分支数量较少,因为如果猫非常重可以直接把车占满,但是猫很轻的话我们就要考虑还要加什么别的猫,因此:将所有猫按从大到小排序,优先放重猫
- 可行性剪枝:当发现目前小猫的重量已经超过缆车承重,就不要再往下搜了
- 最优性剪枝:当发现目前缆车数量已经大于等于当前计算出的缆车最少数量,就不要再搜索了
代码
#include <bits/stdc++.h>using namespace std;const int N = 20;int n, m;
int w[N];
int sum[N];
int ans = N; // 最坏的情况:每只小猫占一辆车void dfs(int u, int k) // u:当前在搜第几只猫 k:当前在搜第几辆车
{// 最优性剪枝if (k >= ans) return;if (u == n){ans = k;return;}for (int i = 0; i < k; i ++ ) // 遍历每一辆车// 可行性剪枝if (sum[i] + w[u] <= m) // 称重符合条件{sum[i] += w[u];dfs(u + 1, k);sum[i] -= w[u]; // 恢复现场}// 新开一辆车sum[k] = w[u];dfs(u + 1, k + 1);sum[k] = 0; // 恢复现场
}int main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);cin >> n >> m;for (int i = 0; i < n; i ++ ) cin >> w[i];// 优化搜索顺序sort(w, w + n);reverse(w, w + n);dfs(0, 0);cout << ans << '\n';
}
数独
原题链接
数独是一种传统益智游戏,你需要把一个 9×9 的数独补充完整,使得数独中每行、每列、每个 3×3 的九宫格内数字 1∼9 均恰好出现一次。
请编写一个程序填写数独。
输入格式
输入包含多组测试用例。
每个测试用例占一行,包含 81 个字符,代表数独的 81 个格内数据(顺序总体由上到下,同行由左到右)。
每个字符都是一个数字(1−9)或一个 .(表示尚未填充)。
您可以假设输入中的每个谜题都只有一个解决方案。
文件结尾处为包含单词 end 的单行,表示输入结束。
输出格式
每个测试用例,输出一行数据,代表填充完全后的数独。
输入样例
4.....8.5.3..........7......2.....6.....8.4......1.......6.3.7.5..2.....1.4......
......52..8.4......3...9...5.1...6..2..7........3.....6...1..........7.4.......3.
end
输出样例
417369825632158947958724316825437169791586432346912758289643571573291684164875293
416837529982465371735129468571298643293746185864351297647913852359682714128574936
题意
填好数独,保证每行每列、每个3x3方块都包含1-9
思路
先做一个小优化,看比如说一个3x3小方格中有哪些数字没被用过,随意选择一个格子,然后对这些数字依次枚举搜索即可
优化:
- 优化搜索顺序:选择格子时,尽量选择分支数量较少的格子,比如说一个格子有2种填法,另一个格子有5种,那肯定优先选择2种的
- 可行性剪枝:一旦与行列九宫格重复时就不要继续搜了
- 位运算优化: 特殊优化,可以用一个九位的二进制数表示每一行数使用的状态
比如:0 1 0 0 1 1 1 0 0 可以用来表示2 5 6 7还没用其他数字用过了
我们考虑这一位上能不能填这个数时,应该考虑二进制数的交集,即在行、列、九宫格的二进制数列上,这个数字都为1,表示在行、列、九宫格内这个数字都没有被使用,我们才能用这个数(直接按位与&)
这里有个比循环九次更好的办法——lowbit
lowbit运算可以帮助我们在O(1)的时间复杂度内,返回当前数里的最后一个1,因此用lowbit循环就可以抠出来所有的1
好难啊好难啊qaq看代码注释吧还是
代码
#include <bits/stdc++.h>using namespace std;const int N = 9, M = 1 << N;int ones[M]; // 每个二进制数里1的个数
int mapp[M]; // 把二进制数换成第几位是1
int row[N], col[N], cell[3][3];
char str[100];void init() // 初始化,将所有位置都标记成没用过(也就是标记成1)
{for (int i = 0; i < N; i ++ ) row[i] = col[i] = (1 << N) - 1;for (int i = 0; i < 3; i ++ )for (int j = 0; j < 3; j ++ )cell[i][j] = (1 << N) - 1;
}void draw(int x, int y, int t, bool is_set) // 在(x,y)这个位置填上/删去t 填上的话is_set为true 删去为false
{if (is_set) str[x * N + y] = '1' + t; // t属于0-8 要把它换算成1-9else str[x * N + y] = '.';int v = 1 << t; // t换算到在每一行的位置if (!is_set) v = -v; // 若为清空操作则取反row[x] -= v;col[y] -= v;cell[x / 3][y / 3] -= v;
}int lowbit(int x) // 返回二进制数的最后一个1以及这个1之后的所有0
{return x & -x;
}int get(int x, int y) // 返回(x,y)能填的数字(二进制序列)
{return row[x] & col[y] & cell[x / 3][y / 3];
}bool dfs(int cnt)
{if (!cnt) return true; // 全部填完int minv = 10; // 首先找分支数最少的空格,将最少的分支数赋给maxxint x, y;for (int i = 0; i < N; i ++ )for (int j = 0; j < N; j ++ )if (str[i * N + j] == '.') // 格子为空可以填数字{int state = get(i, j); // 该格子能填的数字的交集if (ones[state] < minv){minv = ones[state]; // 更新最少分支数x = i, y = j; // xy存的就是分支数量最少的格子的坐标}}int state = get(x, y);for (int i = state; i; i -= lowbit(i)){int t = mapp[lowbit(i)]; // 得到最后一个1所在的位置draw(x, y, t, true); // 把t填进去if (dfs(cnt - 1)) return true; // 成功直接返回truedraw(x, y, t, false); // 失败就把填进去的值再删掉}return false;
}int main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);// 打表得到ones和mappfor (int i = 0; i < N; i ++ ) mapp[1 << i] = i; // 将所有2^k转化成k(也就是返回二进制数里唯一一个1的位置)for (int i = 0; i < 1 << N; i ++ )for (int j = 0; j < N; j ++ )ones[i] += i >> j & 1; // 记下每个二进制数里1的个数while (cin >> str, str[0] != 'e'){init();int cnt = 0; // 有多少位置没填for (int i = 0, k = 0; i < N; i ++ )for (int j = 0; j < N; j ++, k ++ )if (str[k] != '.') // 位置不空就把值填进去{int t = str[k] - '1';draw(i, j, t, true);}else cnt ++ ; // 位置空就累加空位的数量dfs(cnt);puts(str);}
}
木棒
原题链接
乔治拿来一组等长的木棒,将它们随机地砍断,使得每一节木棍的长度都不超过 50 个长度单位。
然后他又想把这些木棍恢复到为裁截前的状态,但忘记了初始时有多少木棒以及木棒的初始长度。
请你设计一个程序,帮助乔治计算木棒的可能最小长度。
每一节木棍的长度都用大于零的整数表示。
输入格式
输入包含多组数据,每组数据包括两行。
第一行是一个不超过 64 的整数,表示砍断之后共有多少节木棍。
第二行是截断以后,所得到的各节木棍的长度。
在最后一组数据之后,是一个零。
输出格式
为每组数据,分别输出原始木棒的可能最小长度,每组数据占一行。
数据范围
数据保证每一节木棍的长度均不大于 50。
输入样例
9
5 2 1 5 2 1 5 2 1
4
1 2 3 4
0
输出样例
6
5
题意
给出一些数,将其分成若干组,使每一组总和相等,问最小的总和是多少
思路
木棒:每一组的总和
木棍:题目中输入的数据
先从小到大枚举木棒的长度length,看木棍能不能组成该长度的木棒
优化:
- 所有木棍的总长度sum必须能整除木棒的长度length,才可能有解,不能整除的情况直接回溯不要搜了
- 优化搜索顺序:先枚举比较长的木棍,使之后的分支较少
- 排除等效冗余:
(1) 如果一根木棒里有第一根第二根两根木棍,那么先用第一根和先用第二根达成的效果都是一样的,因此按照组合数方式枚举
(2) 如果当前木棍加到当前木棒中失败,那直接略过后面所有等长木棍
(3) 如果是木棒的第一根木棍失败(说明这根木棍没地方放),则当前状态一定失败,直接回溯不要往下搜了
(4) 如果是木棒的最后一根木棍失败(这里的意思是往下dfs找不到解),则当前状态一定失败(因为放入比这根木棍小的木棍拼接起来的也一定找不到解),直接回溯不要往下搜了
代码
#include <bits/stdc++.h>using namespace std;const int N = 70;int n;
int w[N], sum, length; // w[i]:每根小棍长度 sum:所有小棍总长度 length:每组总和
bool st[N]; // 小棍有没有用过bool dfs(int u, int s, int start) // u:当前枚举到哪根大棍 s:当前大棍长度 start:开始位置
{if (u * length == sum) return true; // 符合条件if (s == length) return dfs(u + 1, 0, 0); // 这根木棍长度已达要求,开下一根木棍// 优化3(1):从start开始枚举for (int i = start; i < n; i ++ ) // 从start开始遍历木棍{if (st[i]) continue; // 已遍历if (s + w[i] > length) continue; // 可行性剪枝st[i] = true; // 更改状态if (dfs(u, s + w[i], i + 1)) return true; // 下一层遍历st[i] = false; // 恢复现场// 优化3(3):开头不行就一定不行if (!s) return false;// 优化3(4):结尾不行就一定不行if (s + w[i] == length) return false;// 优化3(2):等长直接略过int j = i;while (j < n && w[j] == w[i]) j ++ ;i = j - 1;}return false;
}int main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);while (cin >> n, n){memset(st, false, sizeof st);sum = 0;for (int i = 0; i < n; i ++ ){cin >> w[i];sum += w[i];}// 优化2:搜索顺序sort (w, w + n);reverse(w, w + n);length = 1;while (1){// 优化1:必须是整数倍if (sum % length == 0 && dfs(0, 0, 0)){cout << length << '\n';break;}length ++ ;}}
}
生日蛋糕
原题链接
7 月 17 日是 Mr.W 的生日,ACM-THU 为此要制作一个体积为 Nπ 的 M 层生日蛋糕,每层都是一个圆柱体。
设从下往上数第 i 层蛋糕是半径为 Ri,高度为 Hi 的圆柱。
当 i < M i<M i<M 时,要求 R i > R i + 1 Ri>Ri+1 Ri>Ri+1 且 Hi > Hi+1。
由于要在蛋糕上抹奶油,为尽可能节约经费,我们希望蛋糕外表面(最下一层的下底面除外)的面积 Q 最小。
令 Q = S π Q=Sπ Q=Sπ ,请编程对给出的 N 和 M,找出蛋糕的制作方案(适当的 Ri 和 Hi 的值),使 S 最小。
除 Q 外,以上所有数据皆为正整数。
输入格式
输入包含两行,第一行为整数 N,表示待制作的蛋糕的体积为 Nπ。
第二行为整数 M,表示蛋糕的层数为 M。
输出格式
输出仅一行,是一个正整数 S(若无解则 S=0)。
数据范围
1 ≤ N ≤ 10000,
1 ≤ M ≤ 20
输入样例
100
2
输出样例
68
题意
多层蛋糕,给出总体积总层数,可以自定义每一层半径和高度,使得从上往下看的总面积和总侧面积之和最小,求最小值
思路
首先明确我们的目的是让 2 * Rm * hm + 2 * Rm-1 * hm-1 + … + 2 * R1 * h1 + Rm2 最小(省去了所有的 π π π)
优化:
- 优化搜索顺序:分支少的先搜,从大到小枚举
(1) 要先搜面积大的,因此自底向上搜
(2) 半径是平方级别,高是一次方,半径对体积影响更大,因此先枚举半径 - 可行性剪枝:
(1) 设从上往下为1-m层,第 u 层的半径记为 Ru,一定比 u 大,且比 Ru+1 - 1 小,同时,我们设第 u 层下方的所有体积为 V,那么前 u 层的体积就是 n − V n - V n−V,即有 n − V > = R u 2 h u n - V >= R_u^2h_u n−V>=Ru2hu,放缩后有 R u < = n − V R_u <= \sqrt{n - V} Ru<=n−V
据此得到: u < = R u < = m i n { R u + 1 − 1 , n − V } u <= R_u <= min\{R_{u+1}-1, \sqrt{n-V}\} u<=Ru<=min{Ru+1−1,n−V}
(2) 同时,Hu也>=u,且比 Hu+1小, n − V > = R u 2 h u n - V >= R_u^2h_u n−V>=Ru2hu,放缩后有 h u < = n − V R 2 h_u<= \frac{n-V}{R^2} hu<=R2n−V
据此得到: u < = h u < = m i n { h u + 1 − 1 , n − V R 2 } u <= h_u <= min\{h_{u+1}-1, \frac{n-V}{R^2}\} u<=hu<=min{hu+1−1,R2n−V} - 最小体积是半径和高都取1时,因此可以预处理一下前 u 层的体积最小值 m i n v ( u ) minv(u) minv(u)和表面积最小值 m i n s ( u ) mins(u) mins(u),需要满足以下两个条件才有往下搜的必要,否则直接回溯:
V + m i n v ( u ) < = n V+minv(u)<=n V+minv(u)<=n
s + m i n s ( u ) < a n s s+mins(u)<ans s+mins(u)<ans - 已知: n − V = ∑ k = 1 u R k 2 h k n-V=\sum_{k=1}^{u}R_k^2h_k n−V=∑k=1uRk2hk
并且: S 1 → u = ∑ k = 1 u 2 R k h k = 2 R u + 1 ∑ k = 1 u R u h R u + 1 > 2 R u + 1 ∑ k = 1 u R u 2 h S_{1\rightarrow u}=\sum_{k=1}^{u}2R_kh_k=\frac{2}{R_{u+1}}\sum_{k=1}^{u}R_uhR_{u+1}>\frac{2}{R_{u+1}}\sum_{k=1}^{u}R_u^2h S1→u=∑k=1u2Rkhk=Ru+12∑k=1uRuhRu+1>Ru+12∑k=1uRu2h
因此: S 1 → u > 2 ( n − V ) R u + 1 S_{1\rightarrow u}>\frac{2(n-V)}{R_{u+1}} S1→u>Ru+12(n−V)
所以当 s + 2 ( n − V ) R u + 1 > = a n s s+\frac{2(n-V)}{R_{u+1}}>=ans s+Ru+12(n−V)>=ans时,已经不可能是最优解了,直接回溯
(好难…疯掉TAT
代码
#include <bits/stdc++.h>using namespace std;const int N = 25, inf = 1e9;int n, m;
int minv[N], mins[N]; // 分别表示每一层及该层上方的最小体积和最小表面积
int R[N], H[N]; // 表示每一层的半径和高
int ans = inf;void dfs(int u, int v, int s) // u:当前层数 v:当前体积 s:当前表面积
{if (v + minv[u] > n) return; // 优化3if (s + mins[u] >= ans) return; // 优化3if (s + 2 * (n - v) / R[u + 1] >= ans) return; // 优化4if (!u) //已全部搜完{if (v == n) ans = s;return;}// 优化1:从大到小枚举for (int r = min(R[u + 1] - 1, (int)sqrt(n - v)); r >= u; r -- ) // 优化2for (int h = min(H[u + 1] - 1, (n - v) / r / r); h >= u; h -- ) // 优化2{int t = 0;if (u == m) t = r * r; // 如果是最底层,要加上底面积R[u] = r, H[u] = h; // 更新RHdfs(u - 1, v + r * r * h, s + 2 * h * r + t);}
}int main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);cin >> n >> m;// 打表做出minv minsfor (int i = 1; i <= m; i ++ ){minv[i] = minv[i - 1] + i * i * i;mins[i] = mins[i - 1] + 2 * i * i;}R[m + 1] = H[m + 1] = inf; // 设置哨兵dfs(m, 0, 0);if (ans == inf) ans = 0; // 无满足要求的情况cout << ans << '\n';
}
相关文章:

【搜索】DFS剪枝与优化
算法提高课笔记 目录 小猫爬山题意思路代码 数独题意思路代码 木棒题意思路代码 生日蛋糕题意思路代码 剪枝是什么意思呢? 我们知道,不管是内部搜索还是外部搜索,都可以形成一棵搜索树,如果将搜索树全部遍历一遍,效率…...
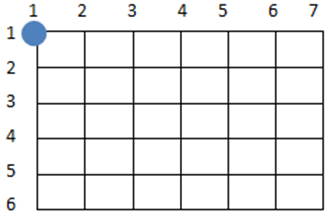
dfs之卒的遍历
题面 题目描述 在一张nm 的棋盘上(如 6 行 7 列)的最左上角(1,1) 的位置有一个卒。该卒只能向下或者向右走,且卒采取的策略是先向下,下边走到头就向右,请问从(1,1) 点走到 (n,m) 点可以怎样走,输出这些走法…...

Springboot整合activiti5,达梦数据库,mybatis中间件
Springboot整合activiti5,达梦数据库,mybatis中间件 问题现象解决方案 问题现象 由于工作流引擎不支持达梦数据库以及国产中间件,所以我们引入的时候会报错,这个时候就需要去改造代码和配置文件。各种文档和资料查找一天…...
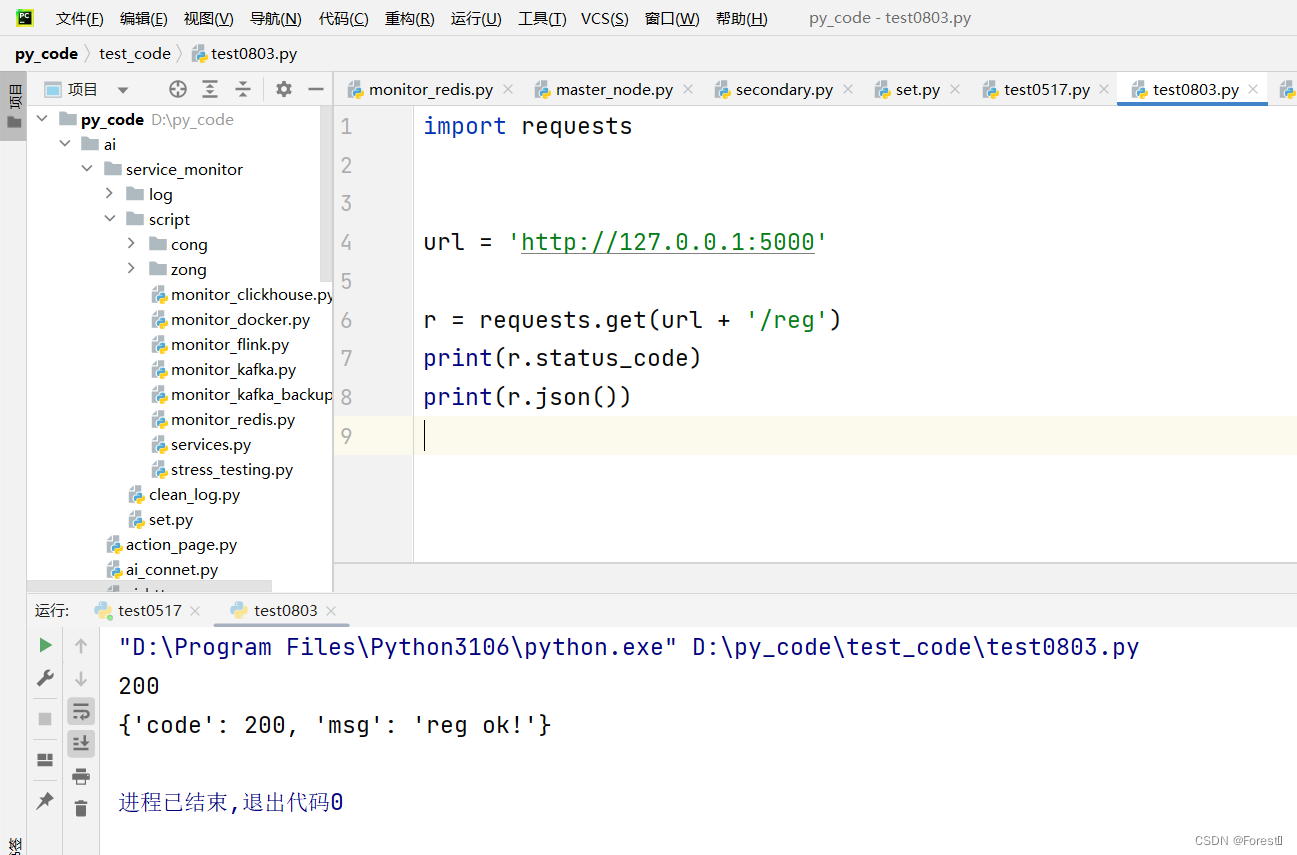
使用Python + Flask搭建web服务
示例脚本 from flask import Flask# 获取一个实例对象 app Flask(__name__)# 1、注册 app.route(/reg, methods[get]) def reg():return {code: 200,msg: reg ok!}# 2、登录 app.route(/login, methods[get]) def login():return login ok!if __name__ __main__:…...

Winform 打开文件夹、文件、拖拽上传
参考原文:https://blog.csdn.net/u012543266/article/details/21834073 1、打开文件 private void button1_Click(object sender, EventArgs e){OpenFileDialog dialog new OpenFileDialog();dialog.Multiselect true;//该值确定是否可以选择多个文件dialog.Titl…...
热评国内AI四小龙:此一时彼一时,彼此彼此
引言:阿里“清仓”全部持股 商汤科技表示“没啥事” 【科技明说 | 热点关注】 作为国内AI领域的知名科技上市公司,商汤科技SenseTime的一举一动都牵动着业内人士的心。 然而,商汤科技的财报表现没有出奇制胜,却让不…...

[国产MCU]-BL602开发实例-GPIO控制
GPIO与控制 文章目录 GPIO与控制1、GPIO介绍2、GPIO管理相关API介绍3、硬件准备4、软件准备5、代码实现3.1 GPIO输出3.2 GPIO输入3.3 GPIO中断BL602的GLB(Global Register)是芯片通用全局设定模块,主要包含了时钟管理、复位管理、总线管理、内存管理以及GPIO管理等功能。 本文…...

Firefox 配置 Burp_proxy 和 证书
安装代理拓展 安装拓展: chrome : switchomega firefox : foxyproxy 创建代理 : 127.0.0.1:8080 安装burp证书 先开启burp,然后切换到 burp 的代理访问 https://burp/ 下载证书打开firefox设置 - 搜索”证书“ -…...
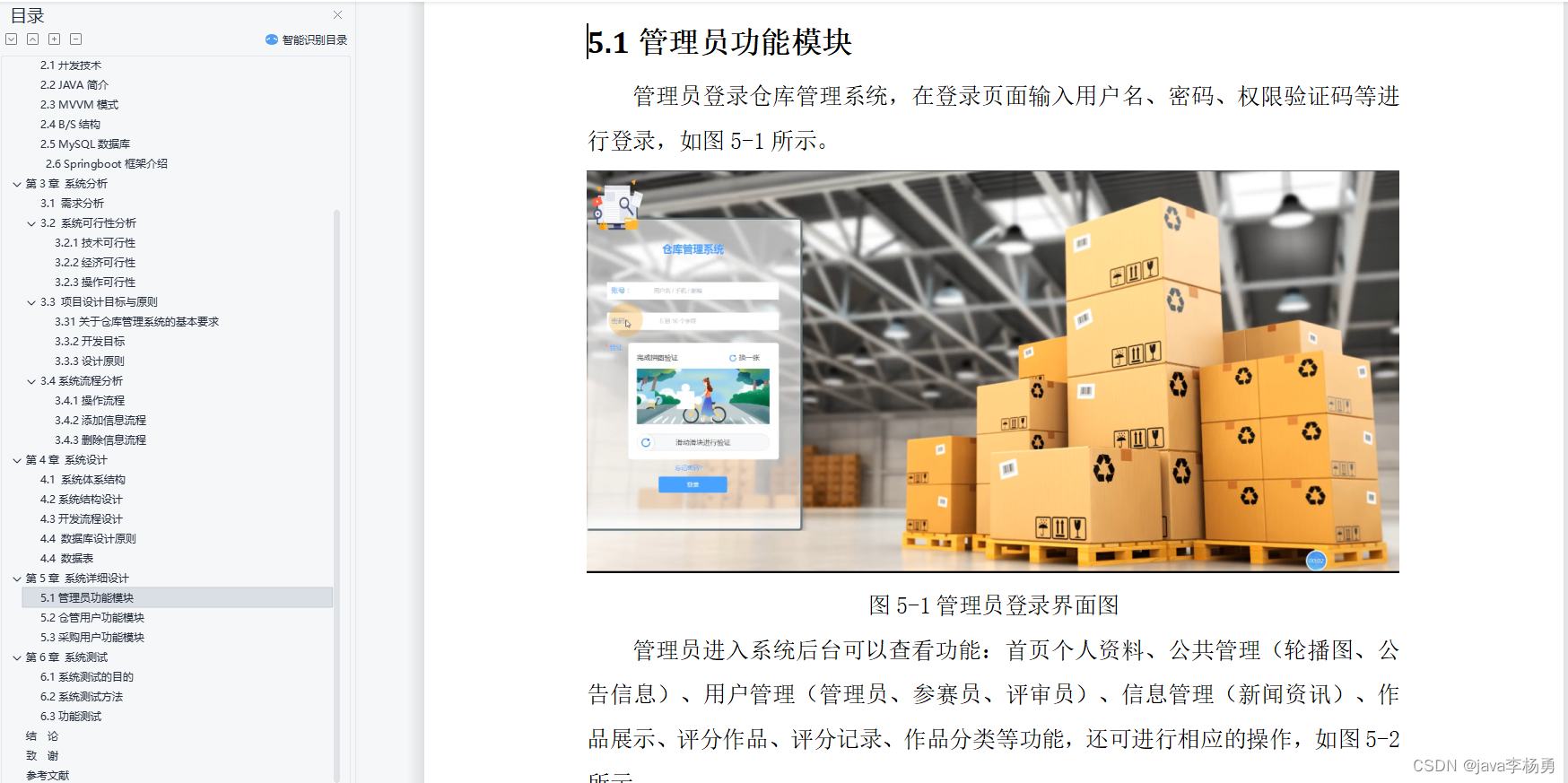
基于Java+SpringBoot+Vue前后端分离仓库管理系统详细设计和实现
博主介绍:✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专…...

PyTorch Lightning教程七:可视化
本节指导如何利用Lightning进行可视化和监控模型 为何需要跟踪参数 在模型开发中,我们跟踪感兴趣的值,例如validation_loss,以可视化模型的学习过程。模型开发就像驾驶一辆没有窗户的汽车,图表和日志提供了窗口,让我们…...

后端开发2.mongdb的集成
使用docker安装 安装 拉取镜像 docker pull mongo:4.4.14-focal 创建容器 docker run -itd --name mongo -p 8036:27017 mongo:4.4.14-focal --auth 配置管理员 进入容器 docker exec -it mongo bash 进入终端 mongo 进入admin数据库 use admin 创建管理员账户 db.c…...

Unity面板究极优化
首先对于大项目来说UI首选一定的UGUI,目前没有啥可选的余地。多一点都是对性能的负担,UGUI底层基于多线程技术,可以有效分担压力,对于一些不是那么重的面板几乎无感。 无论其他面板只是在此基础上修改的,但每多一层&am…...

C# App.config和Web.config加密
步骤1:创建加密命令 使用ASP.NET提供的命令工具aspnet_regiis来创建加密命令。 1、打开控制台窗口,在命令行中输入以下命令: cd C:\Windows\Microsoft.NET\Framework\v4.xxxxx aspnet_regiis.exe -pef connectionStrings "C:\MyAppFo…...
(Python3))
力扣:50. Pow(x, n)(Python3)
题目: 实现 pow(x, n) ,即计算 x 的整数 n 次幂函数(即,xn )。 来源:力扣(LeetCode) 链接:力扣 示例: 示例 1: 输入:x 2.00000, n 1…...
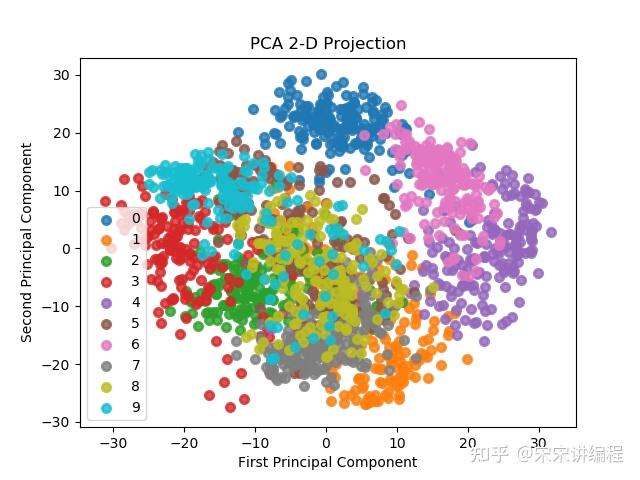
scikit-plot 使用笔记
scikit-plot是基于sklearn和Matplotlib的库,主要的功能是对训练好的模型进行可视化。 安装: pip install scikit-plot 功能1:评估指标可视化 scikitplot.metrics.plot_confusion_matrix快速展示模型预测结果和标签计算得到的混淆矩阵。 im…...

2024考研408-计算机网络 第五章-传输层学习笔记
文章目录 前言一、传输层提供的服务1.1、传输层的功能1.2、传输层的两个协议(TCP、UDP)1.3、传输层的寻址与端口(常见端口介绍) 二、UDP协议2.1、认识UDP功能和特点2.2、UDP首部格式2.3、UDP伪首部字段分析2.4、伪首部校验UDP用户…...

【JS】一道解构面试题
文章目录 [TOC] 一道解构面试题题目运行结果 原理概念数组迭代器 答案答案(1)、在对象中添加一个数组迭代器1.使用临时数组添加迭代器2. 对象值输出结果3.使用Object.values(this);拿到对象的值 答案(2)、在对象原型上添加数组迭代器1.按步骤实现数组迭代器2. 简化步骤 答案(3)…...

24v转3.3v输出3A用什么芯片
问:客户需要一个能够将24V输入电压转换为3.3V输出电压,并且能够提供1-3A的电流输出的芯片。还希望它能够内置MOS管。有什么推荐的型号吗?(vin24v、5v,vout3.3v,Io1-3A) 答:推荐使用…...
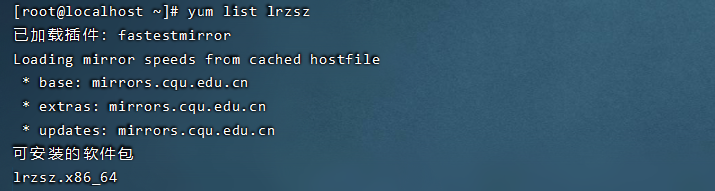
在Linux中安装lrzsz(yum命令使用)
在Linux中安装lrzsz(yum命令使用) 操作步骤: 1、搜索lrzsz安装包,命令为yum list lrzsz 2、使用yum命令在线安装,命令为yum install lrzsz.x86_64 注意事项: Yum(全称为 Yellow dog Updater, Modified)是一个在Fedor…...
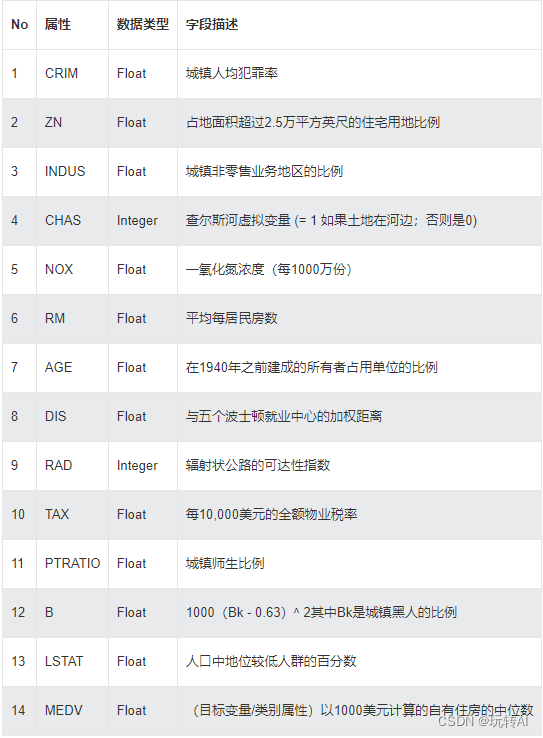
机器学习基础08-回归算法矩阵分析(基于波士顿房价(Boston House Price)数据集)
回归算法通常涉及到使用矩阵来表示数据和模型参数。线性回归是最常见的回归算法之一,它可以用矩阵形式来表示。 考虑一个简单的线性回归模型: y m x b y mx b ymxb,其中 y y y 是因变量, x x x 是自变量, m m m 是…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...
