【学习日志】2023.Aug.6,支持向量机的实现
2023.Aug.6,支持向量机的实现
参考了大佬的代码,但有些地方似乎还有改进的空间,我加了注释
#coding=utf-8
#Author:Dodo
#Date:2018-12-03
#Email:lvtengchao@pku.edu.cn
#Blog:www.pkudodo.com
'''
数据集:Mnist
训练集数量:60000(实际使用:1000)
测试集数量:10000(实际使用:100)
------------------------------
运行结果:正确率:99%运行时长:50s流程:
SVM本身是一个二分类器,它希望找到一个最优分隔面,
把正样本和负样本分离开,使得最大化那些距离分隔面最近的样本点。
但是实际中的数据并不总是线性可分的,于是有了软间隔。软间隔是说允许若干点违反分隔面,但是会有惩罚;
对于整体数据模式就不是线性可分的数据集,可以使用核技巧,
核技巧是说使用非线性变换把输入数据映射到高维的特征空间中,然后在高维空间使用线性情况下的方法找到最优分隔面。具体地,
SVM找最优分隔面的问题,可以转化成凸二次规划模型。
考虑到原问题不宜求解,求它的对偶问题alpha;
然后,使用KKT条件,从对偶问题的解出发,解出原问题的解,即分隔面的参数。
更具体地,求解对偶问题的算法可以使用SMO(序列最小最优化算法),
该算法首先选两个变量、固定其余变量,将原来的多变量对偶问题,转化成两个变量的优化问题求解;
然后迭代达到停机条件,得到对偶问题的解alpha。
一般地,第一个变量是违反KKT条件的那个样本i所对应的对偶变量alpha_i,第二个变量是选改变尽可能大的变量。'''import time
import numpy as np
import math
import randomdef loadData(fileName):'''加载文件:param fileName:要加载的文件路径:return: 数据集和标签集'''#存放数据及标记dataArr = []; labelArr = []#读取文件fr = open(fileName)#遍历文件中的每一行for line in fr.readlines():#获取当前行,并按“,”切割成字段放入列表中#strip:去掉每行字符串首尾指定的字符(默认空格或换行符)#split:按照指定的字符将字符串切割成每个字段,返回列表形式curLine = line.strip().split(',')#将每行中除标记外的数据放入数据集中(curLine[0]为标记信息)#在放入的同时将原先字符串形式的数据转换为0-1的浮点型dataArr.append([int(num) / 255 for num in curLine[1:]])# ?why do we do that ?#将标记信息放入标记集中#放入的同时将标记转换为整型#数字0标记为1 其余标记为-1if int(curLine[0]) == 0:labelArr.append(1)else:labelArr.append(-1)#返回数据集和标记return dataArr, labelArrclass SVM:'''SVM类'''def __init__(self, trainDataList, trainLabelList, sigma = 10, C = 200, toler = 0.001):'''SVM相关参数初始化:param trainDataList:训练数据集,训练数据的特征:param trainLabelList: 训练测试集,训练数据的标签:param sigma: 高斯核中分母的σ:param C:软间隔中的惩罚参数:param toler:松弛变量注:关于这些参数的初始值:参数的初始值大部分没有强要求,请参照书中给的参考,例如C是调和间隔与误分类点的系数,在选值时通过经验法依据结果来动态调整。(本程序中的初始值参考于《机器学习实战》中SVM章节,因为书中也使用了该数据集,只不过抽取了很少的数据测试。参数在一定程度上有参考性。)如果使用的是其他数据集且结果不太好,强烈建议重新通读所有参数所在的公式进行修改。例如在核函数中σ的值高度依赖样本特征值范围,特征值范围较大时若不相应增大σ会导致所有计算得到的核函数均为0'''self.trainDataMat = np.mat(trainDataList) #训练数据集self.trainLabelMat = np.mat(trainLabelList).T #训练标签集,为了方便后续运算提前做了转置,变为列向量self.m, self.n = np.shape(self.trainDataMat) #m:训练集数量 n:样本特征数目self.sigma = sigma #高斯核分母中的σself.C = C #惩罚参数self.toler = toler #松弛变量self.k = self.calcKernel() #核函数(初始化时提前计算)self.b = 0 #SVM中的偏置bself.alpha = [0] * self.trainDataMat.shape[0] # α 长度为训练集数目;# both alpha and b need to be worked out through training * self.trainLabelMat[i, 0]self.E = [0 for i in range(self.trainLabelMat.shape[0])] #error, used to select the 2nd var in SVM #SMO运算过程中的Eiself.supportVecIndex = []def calcKernel(self):'''计算核函数使用的是高斯核 详见“7.3.3 常用核函数” 式7.90:return: 高斯核矩阵'''#初始化高斯核结果矩阵 大小 = 训练集长度m * 训练集长度m#k[i][j] = Xi * Xjk = [[0 for i in range(self.m)] for j in range(self.m)]#大循环遍历Xi,Xi为式7.90中的xfor i in range(self.m):#每100个打印一次#不能每次都打印,会极大拖慢程序运行速度#因为print是比较慢的if i % 100 == 0:print('construct the kernel:', i, self.m)#得到式7.90中的XX = self.trainDataMat[i, :]#小循环遍历Xj,Xj为式7.90中的Z# 由于 Xi * Xj 等于 Xj * Xi,一次计算得到的结果可以# 同时放在k[i][j]和k[j][i]中,这样一个矩阵只需要计算一半即可#所以小循环直接从i开始for j in range(i, self.m):#获得ZZ = self.trainDataMat[j, :]#先计算||X - Z||^2result = (X - Z) * (X - Z).T#分子除以分母后去指数,得到的即为高斯核结果result = np.exp(-1 * result / (2 * self.sigma**2))#将Xi*Xj的结果存放入k[i][j]和k[j][i]中k[i][j] = resultk[j][i] = result#返回高斯核矩阵return kdef isSatisfyKKT(self, i):'''查看第i个α是否满足KKT条件:param i:α的下标:return:True:满足False:不满足'''gxi =self.calc_gxi(i)yi = self.trainLabelMat[i]# print((yi * gxi >= 1),yi, gxi,type(yi), type(self.alpha[i]))#判断依据参照“7.4.2 变量的选择方法”中“1.第1个变量的选择”#式7.111到7.113#--------------------#依据7.111if (math.fabs(self.alpha[i]) < self.toler) and (yi * gxi >= 1):return True#依据7.113elif (math.fabs(self.alpha[i] - self.C) < self.toler) and (yi * gxi <= 1):return True#依据7.112elif (self.alpha[i] > -self.toler) and (self.alpha[i] < (self.C + self.toler)) \and (math.fabs(yi * gxi - 1) < self.toler):return Truereturn Falsedef calc_gxi(self, i):'''计算g(xi)依据“7.101 两个变量二次规划的求解方法”式7.104:param i:x的下标:return: g(xi)的值'''#初始化g(xi)gxi = 0#因为g(xi)是一个求和式+b的形式,普通做法应该是直接求出求和式中的每一项再相加即可#但是读者应该有发现,在“7.2.3 支持向量”开头第一句话有说到“对应于α>0的样本点#(xi, yi)的实例xi称为支持向量”。也就是说只有支持向量的α是大于0的,在求和式内的#对应的αi*yi*K(xi, xj)不为0,非支持向量的αi*yi*K(xi, xj)必为0,也就不需要参与#到计算中。也就是说,在g(xi)内部求和式的运算中,只需要计算α>0的部分,其余部分可#忽略。因为支持向量的数量是比较少的,这样可以再很大程度上节约时间#从另一角度看,抛掉支持向量的概念,如果α为0,αi*yi*K(xi, xj)本身也必为0,从数学#角度上将也可以扔掉不算#index获得非零α的下标,并做成列表形式方便后续遍历index = [i for i, alpha in enumerate(self.alpha) if alpha != 0]#遍历每一个非零α,i为非零α的下标for j in index:#计算g(xi)gxi += self.alpha[j] * self.trainLabelMat[j] * self.k[j][i]#求和结束后再单独加上偏置bgxi += self.b#返回return gxidef calcEi(self, i):'''计算Ei根据“7.4.1 两个变量二次规划的求解方法”式7.105:param i: E的下标:return:'''#计算g(xi)gxi = self.calc_gxi(i)#Ei = g(xi) - yi,直接将结果作为Ei返回return gxi - self.trainLabelMat[i]def getAlphaJ(self, E1, i):'''SMO中选择第二个变量:param E1: 第一个变量的E1:param i: 第一个变量α的下标:return: E2,α2的下标'''#初始化E2E2 = 0#初始化|E1-E2|为-1maxE1_E2 = -1#初始化第二个变量的下标maxIndex = -1#这一步是一个优化性的算法#实际上书上算法中初始时每一个Ei应当都为-yi(因为g(xi)由于初始α为0,必然为0)#然后每次按照书中第二步去计算不同的E2来使得|E1-E2|最大,但是时间耗费太长了#作者最初是全部按照书中缩写,但是本函数在需要3秒左右,所以进行了一些优化措施#--------------------------------------------------#在Ei的初始化中,由于所有α为0,所以一开始是设置Ei初始值为-yi。这里修改为与α#一致,初始状态所有Ei为0,在运行过程中再逐步更新#因此在挑选第二个变量时,只考虑更新过Ei的变量,但是存在问题#1.当程序刚开始运行时,所有Ei都是0,那挑谁呢?# 当程序检测到并没有Ei为非0时,将会使用随机函数随机挑选一个#2.怎么保证能和书中的方法保持一样的有效性呢?# 在挑选第一个变量时是有一个大循环的,它能保证遍历到每一个xi,并更新xi的值,#在程序运行后期后其实绝大部分Ei都已经更新完毕了。下方优化算法只不过是在程序运行#的前半程进行了时间的加速,在程序后期其实与未优化的情况无异#------------------------------------------------------#获得Ei非0的对应索引组成的列表,列表内容为非0Ei的下标inozeroE = [i for i, Ei in enumerate(self.E) if Ei != 0]#对每个非零Ei的下标i进行遍历for j in nozeroE:#计算E2E2_tmp = self.calcEi(j)#如果|E1-E2|大于目前最大值 # recall "第二个变量的选择标准是希望能够使α2有足够大的变化"if math.fabs(E1 - E2_tmp) > maxE1_E2:#更新最大值maxE1_E2 = math.fabs(E1 - E2_tmp)#更新最大值E2E2 = E2_tmp#更新最大值E2的索引jmaxIndex = j#如果列表中没有非0元素了(对应程序最开始运行时的情况)if maxIndex == -1:maxIndex = iwhile maxIndex == i:#获得随机数,如果随机数与第一个变量的下标i一致则重新随机maxIndex = int(random.uniform(0, self.m))# we hope to find i2 which doesn't equals to i#获得E2E2 = self.calcEi(maxIndex)#返回第二个变量的E2值以及其索引(the index of the 2nd var in SMO 算法)return E2, maxIndexdef train(self, iter = 100):#iterStep:迭代次数,超过设置次数还未收敛则强制停止#parameterChanged:单次迭代中有参数改变则增加1iterStep = 0; parameterChanged = 1#如果没有达到限制的迭代次数以及上次迭代中有参数改变则继续迭代#parameterChanged==0时表示上次迭代没有参数改变,如果遍历了一遍都没有参数改变,说明#达到了收敛状态,可以停止了while (iterStep < iter) and (parameterChanged > 0):#打印当前迭代轮数print('iter:%d:%d'%( iterStep, iter))#迭代步数加1iterStep += 1#新的一轮将参数改变标志位重新置0parameterChanged = 0# using SMO algo to solve that quadratic convex programming#大循环遍历所有样本,用于找SMO中第一个变量for i in range(self.m):#查看第一个遍历是否满足KKT条件,如果不满足则作为SMO中第一个变量从而进行优化if self.isSatisfyKKT(i) == False:#如果下标为i的α不满足KKT条件,则进行优化#第一个变量α的下标i已经确定,接下来按照“7.4.2 变量的选择方法”第二步#选择变量2。由于变量2的选择中涉及到|E1 - E2|,因此先计算E1E1 = self.calcEi(i)#选择第2个变量E2, j = self.getAlphaJ(E1, i)#参考“7.4.1两个变量二次规划的求解方法” P126 下半部分#获得两个变量的标签y1 = self.trainLabelMat[i]y2 = self.trainLabelMat[j]#复制α值作为old值alphaOld_1 = self.alpha[i]alphaOld_2 = self.alpha[j]#依据标签是否一致来生成不同的L和H, # L and H are used to clip aphaNew_2if y1 != y2:L = max(0, alphaOld_2 - alphaOld_1)H = min(self.C, self.C + alphaOld_2 - alphaOld_1)else:L = max(0, alphaOld_2 + alphaOld_1 - self.C)H = min(self.C, alphaOld_2 + alphaOld_1)#如果两者相等,说明该变量无法再优化,直接跳到下一次循环if L == H: continue#计算α的新值#依据“7.4.1两个变量二次规划的求解方法”式7.106更新α2值#先获得几个k值,用来计算事7.106中的分母ηk11 = self.k[i][i]k22 = self.k[j][j]k21 = self.k[j][i]k12 = self.k[i][j]#依据式7.106更新α2,该α2还未经剪切alphaNew_2 = alphaOld_2 + y2 * (E1 - E2) / (k11 + k22 - 2 * k12)#剪切α2if alphaNew_2 < L: alphaNew_2 = Lelif alphaNew_2 > H: alphaNew_2 = H#更新α1,依据式7.109alphaNew_1 = alphaOld_1 + y1 * y2 * (alphaOld_2 - alphaNew_2)#依据“7.4.2 变量的选择方法”第三步式7.115和7.116计算b1和b2b1New = -1 * E1 - y1 * k11 * (alphaNew_1 - alphaOld_1) \- y2 * k21 * (alphaNew_2 - alphaOld_2) + self.bb2New = -1 * E2 - y1 * k12 * (alphaNew_1 - alphaOld_1) \- y2 * k22 * (alphaNew_2 - alphaOld_2) + self.b#依据α1和α2的值范围确定新b # !! something different from that bookif (alphaNew_1 > 0) and (alphaNew_1 < self.C):bNew = b1Newelif (alphaNew_2 > 0) and (alphaNew_2 < self.C):bNew = b2Newelse:bNew = (b1New + b2New) / 2#将更新后的各类值写入,进行更新, # 更新alpha是为了更新E[i]# E[i]值的更新需要用到,alpha[i]和bself.alpha[i] = alphaNew_1self.alpha[j] = alphaNew_2self.b = bNewself.E[i] = self.calcEi(i)self.E[j] = self.calcEi(j)#如果α2的改变量过于小,就认为该参数未改变,不增加parameterChanged值#反之则自增1if math.fabs(alphaNew_2 - alphaOld_2) >= 0.00001:parameterChanged += 1#打印迭代轮数,i值(SMO算法第一个变量的索引),该迭代轮数修改α数目print("iter: %d i:%d, pairs changed %d" % (iterStep, i, parameterChanged))#全部计算结束后,重新遍历一遍α,查找里面的支持向量for i in range(self.m):#如果α>0,说明是支持向量if self.alpha[i] > 0:#将支持向量的索引保存起来self.supportVecIndex.append(i)def calcSinglKernel(self, x1, x2):'''单独计算核函数:param x1:向量1:param x2: 向量2:return: 核函数结果'''#按照“7.3.3 常用核函数”式7.90计算高斯核result = (x1 - x2) * (x1 - x2).Tresult = np.exp(-1 * result / (2 * self.sigma ** 2))#返回结果return np.exp(result)#?? why add np.exp? 我觉得这里直接返回 result就好了def predict(self, x):'''对样本的标签进行预测公式依据“7.3.4 非线性支持向量分类机”中的式7.94:param x: 要预测的样本x:return: 预测结果'''result = 0for i in self.supportVecIndex:#遍历所有支持向量,计算求和式#如果是非支持向量,求和子式必为0,没有必须进行计算#这也是为什么在SVM最后只有支持向量起作用#------------------#先单独将核函数计算出来tmp = self.calcSinglKernel(self.trainDataMat[i, :], np.mat(x))#对每一项子式进行求和,最终计算得到求和项的值result += self.alpha[i] * self.trainLabelMat[i] * tmp#求和项计算结束后加上偏置bresult += self.b#使用sign函数返回预测结果return np.sign(result)def test(self, testDataList, testLabelList):'''测试:param testDataList:测试数据集:param testLabelList: 测试标签集:return: 正确率'''#错误计数值errorCnt = 0#遍历测试集所有样本for i in range(len(testDataList)):#打印目前进度print('test:%d:%d'%(i, len(testDataList)))#获取预测结果result = self.predict(testDataList[i])#如果预测与标签不一致,错误计数值加一if result != testLabelList[i]:errorCnt += 1#返回正确率return 1 - errorCnt / len(testDataList)if __name__ == '__main__':start = time.time()# 获取训练集及标签print('start read transSet')trainDataList, trainLabelList = loadData('../Mnist/mnist_train.csv')# 获取测试集及标签print('start read testSet')testDataList, testLabelList = loadData('../Mnist/mnist_test.csv')#初始化SVM类print('start init SVM')svm = SVM(trainDataList[:1000], trainLabelList[:1000], 10, 200, 0.001)# 开始训练print('start to train')svm.train()# 开始测试print('start to test')accuracy = svm.test(testDataList[:100], testLabelList[:100])print('the accuracy is:%d'%(accuracy * 100), '%')# 打印时间print('time span:', time.time() - start)
相关文章:

【学习日志】2023.Aug.6,支持向量机的实现
2023.Aug.6,支持向量机的实现 参考了大佬的代码,但有些地方似乎还有改进的空间,我加了注释 #codingutf-8 #Author:Dodo #Date:2018-12-03 #Email:lvtengchaopku.edu.cn #Blog:www.pkudodo.com数据集:Mnist 训练集数量࿱…...

LeetCode_动态规划_中等_1749.任意子数组和的绝对值的最大值
目录 1.题目2.思路3.代码实现(Java) 1.题目 给你一个整数数组 nums 。一个子数组 [numsl, numsl1, …, numsr-1, numsr] 的 和的绝对值 为 abs(numsl numsl1 … numsr-1 numsr) 。请你找出 nums 中和的绝对值 最大的任意子数组(可能为空…...

无涯教程-Perl - 环境配置
在开始编写Perl程序之前,让我们了解如何设置我们的Perl环境。 您的系统更有可能安装了perl。只需尝试在$提示符下给出以下命令- $perl -v 如果您的计算机上安装了perl,那么您将收到以下消息: This is perl 5, version 16, subversion 2 (v5.16.2) b…...

QT显示加载动画
文章目录 一、前言二、使用1.FormLoading.h2.FormLoading.cpp 一、前言 项目中在下发指令时,结果异步返回,可能需要一段时间,因此需要用到加载动画。 用的比较简单,就是新建Widget子窗口,放一个Label,使用…...
原型模式(C++)
定义 使用原型实例指定创建对象的种类,然后通过拷贝这些原型来创建新的对象。 应用场景 在软件系统中,经常面临着“某些结构复杂的对象”的创建工作;由于需求的变化,这些对象经常面临着剧烈的变化,但是它们却拥有比较稳定一致的…...

web浏览器打开本地exe应用
一、如何使web浏览器打开本地exe应用? 浏览器打开本地exe程序我们可以使用ActiveXObject方法,但是只支持IE,谷歌、火狐等浏览器并不支持此操作。 那问题来了,我们又该如何操作? 经过本博主的不断学习探索终于找到了一…...
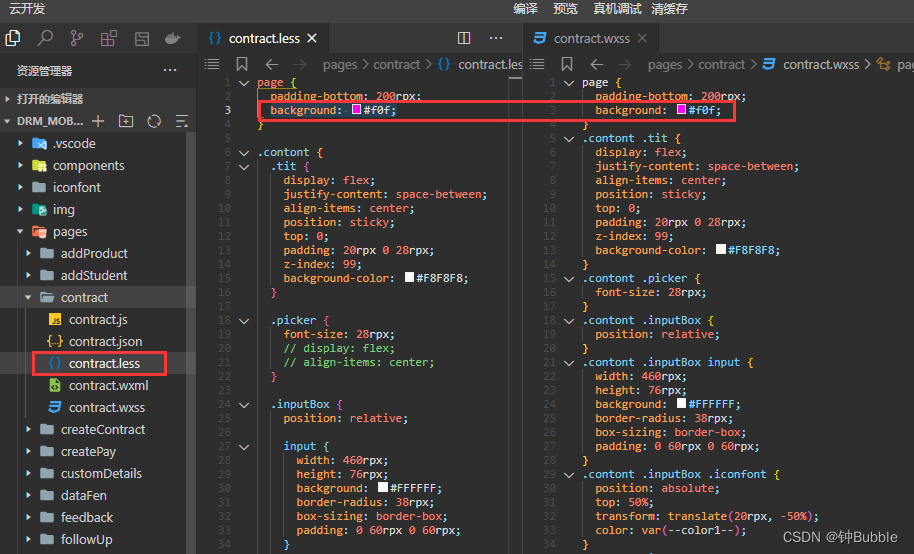
微信小程序如何配置并使用less?
1,检查微信开发者工具(工具版本1.03)————这步很重要不然后面按步骤实行后会发现急死你也还是不管用,我之前死在过这一步,所以大家不要再次踩坑了 ~ ~ 。。。 2,在VScode中下载Less插件 3,…...

【Spring】反射动态修改Bean实例的私有属性值
Cannot cast org.springframework.http.client.InterceptingClientHttpRequestFactory to org.springframework.http.client.OkHttp3ClientHttpRequestFactory 由于RestTemplate在自定义初始化时顺序比较早,想在启动后跟进yum或者注解配置修改初始化的值时ÿ…...

MySQL DDL 数据定义
文章目录 1.创建数据库2.删除数据库3.查看所有数据库4.查看当前数据库5.选择数据库6.创建数据表7.查看 MySQL 支持的存储引擎和默认的存储引擎8.删除数据表9.查看数据库的数据表10.查看表结构11.查看建表语句12.重命名数据表13.增加、删除和修改字段自增长14.增加、删除和修改数…...

Ventoy 设置VTOY_MAX_SEARCH_LEVEL = 0只扫描U盘根目录 不扫码子目录
在镜像分区/media/yeqiang/Ventoy创建目录ventory,目录内创建文件ventoy.json,内容如下 {"control":[{ "VTOY_MAX_SEARCH_LEVEL": "0" }] }采用系统默认的utf-8编码。 参考: search path . Ventoy Plugin.e…...

vue3父子同信的双向数据实现
前言: 我们知道的是,父传子的通信,和子传父的通信,那如何实现父子相互通信的呢? (vue3中)v-model 和modelValue结合使用,在vue2中使用的是.sync 在父组件的写法 <template> <Son v-model"num" /&…...

Shiro是什么?为什么要用Shiro?
前言 本文小新为大家带来 Shiro入门概述 相关知识,具体内容包括Shiro是什么,为什么要用 Shiro,Shiro与Spring Security 的对比,Shiro的基本功能(包括:基本功能框架,功能简介)&#x…...
Vue3+Vite+Pinia+Naive后台管理系统搭建之九:layout 动态路由布局
前言 如果对 vue3 的语法不熟悉的,可以移步Vue3.0 基础入门,快速入门。 1. 系统页面结构 由 menu,面包屑,用户信息,页面标签,页面内容构建 2. 创建页面 创建 src/pages/layout.vue 布局页 创建 sr…...
从零开始学Python(Ⅰ)基本变量与数据类型
🥳🥳Welcome Huihuis Code World ! !🥳🥳 接下来看看由辉辉所写的关于Python的相关操作吧 目录 🥳🥳Welcome Huihuis Code World ! !🥳🥳 一.关于Python的基本知识(变量…...
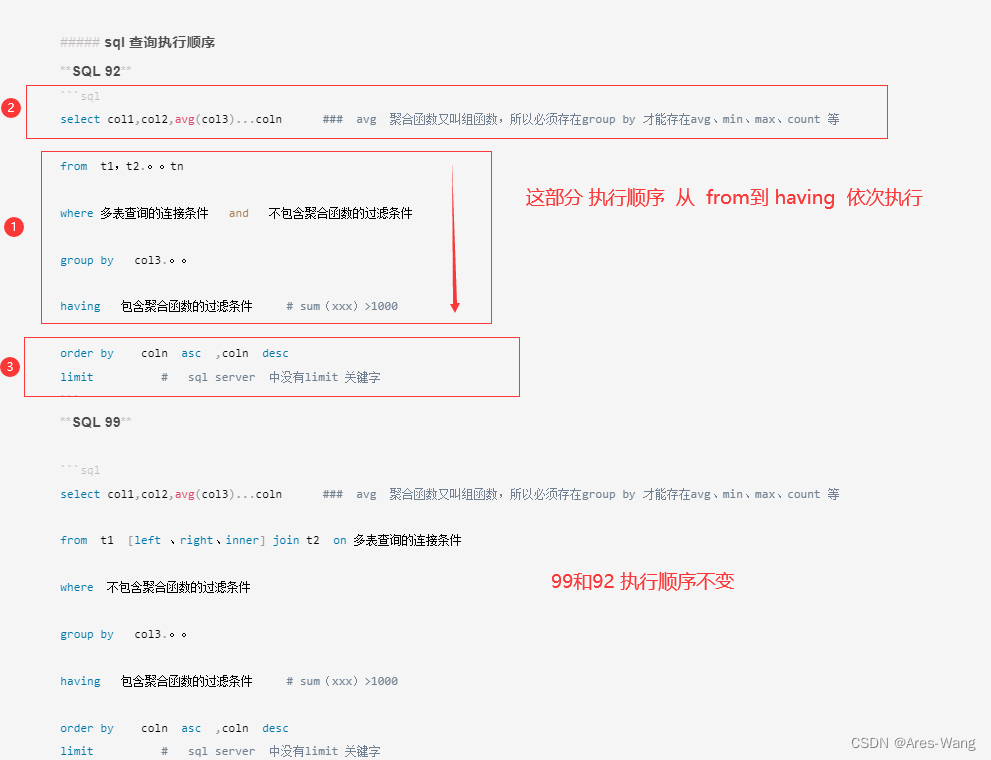
SQL ASNI where from group order 顺序 where和having,SQL底层执行原理
SQL语句执行顺序: from–>where–>group by -->having — >select --> order 第一步:from语句,选择要操作的表。 第二步:where语句,在from后的表中设置筛选条件,筛选出符合条件的记录。 …...
 新机 安装Cocoapods)
Mac M2 Ventura(13.3) 新机 安装Cocoapods
1.执行命令: sudo gem install cocoapods 因为是新机,内置的ruby版本是(2.6.0)太低,会报错 所以需要安装新的ruby版本 2.如果已经安装了低版本的homebrew,可以先卸载: 卸载: /b…...

Unity 引擎做残影效果——2、屏幕后处理方式
Unity实现残影效果 大家好,我是阿赵。 这里继续介绍Unity里面做残影的方法。之前介绍了BakeMesh的方法做残影,这一期介绍的是用屏幕后处理的方法做残影。 一、原理 之前的BakeMesh方法,是真的生成了很多个网格模型在场景里面。如果用后处理做…...
考研算法38天:反序输出 【字符串的翻转】
题目 题目收获 很简单的一道题,但是还是有收获的,我发现我连scanf的字符串输入都忘记咋用了。。。。。我一开始写的 #include <iostream> #include <cstring> using namespace std;void deserve(string &str){int n str.size();int…...

“深入解析JVM:探秘Java虚拟机的工作原理“
标题:深入解析JVM:探秘Java虚拟机的工作原理 摘要:本文将深入探讨Java虚拟机(JVM)的工作原理,包括类加载、内存管理、垃圾回收、即时编译等关键概念。通过详细解析JVM的各个组成部分,读者将能够…...
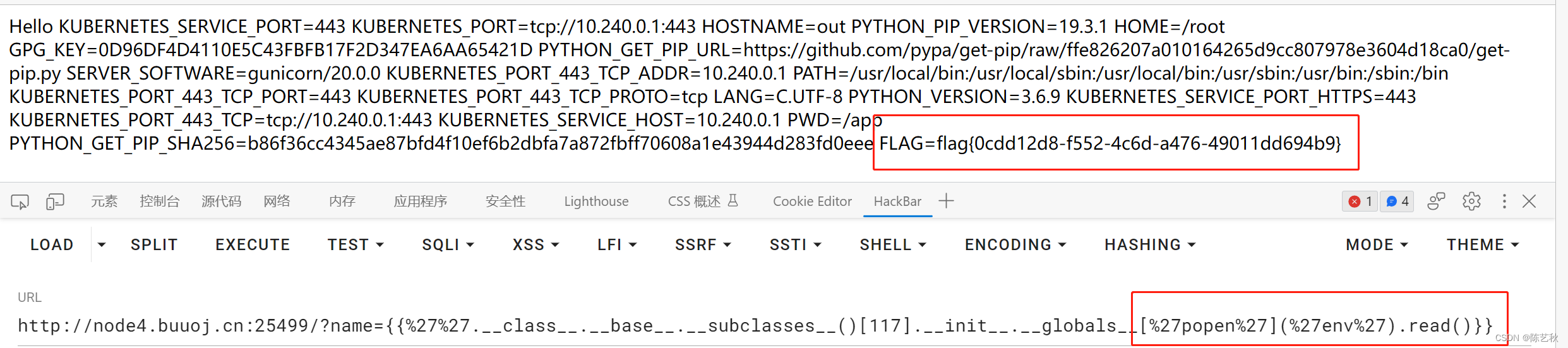
[Flask]SSTI1
根据题目提示,这关应该是基于Python flask的模版注入,进入靶场环境后就是一段字符串,而且没有任何提示,有点难受,主要是没有提示注入点 随机尝试一下咯,首先尝试一下guest,GET传参 但是没有反应…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...
