最小二乘问题和非线性优化
最小二乘问题和非线性优化
- 0.引言
- 1.最小二乘问题
- 2.迭代下降法
- 3.最速下降法
- 4.牛顿法
- 5.阻尼法
- 6.高斯牛顿(GN)法
- 7.莱文贝格马夸特(LM)法
- 8.鲁棒核函数
0.引言
转载自此处,修正了一点小错误。
1.最小二乘问题
在求解 SLAM 中的最优状态估计问题时,我们一般会得到两个变量,一个是由传感器获得的实际观测值 z \boldsymbol{z} z,一个是根据目前估计的状态量和观测模型计算出来的预测值 h ( x ) h(\boldsymbol{x}) h(x)。求解最优状态估计问题时通常我们会尝试最小化预测值和观测值计算出的残差平方(使用平方是为了统一正负号的影响),即求解以下最小二乘问题:
x ∗ = arg min x ∣ ∣ z − h ( x ) ∣ ∣ 2 \boldsymbol{x}^* = \arg\min_{\boldsymbol{x}}||\boldsymbol{z} - h(\boldsymbol{x})||^2 x∗=argxmin∣∣z−h(x)∣∣2
如果观测模型是线性模型,则上式转化为线性最小二乘问题:
x ∗ = arg min x ∣ ∣ z − H x ∣ ∣ 2 \boldsymbol{x}^* = \arg\min_{\boldsymbol{x}}||\boldsymbol{z} - \boldsymbol{H}\boldsymbol{x}||^2 x∗=argxmin∣∣z−Hx∣∣2
对于线性最小二乘问题,我们可以直接求闭式解: x ∗ = − ( H T H ) − 1 H T z \boldsymbol{x}^* = -(\boldsymbol{H}^T\boldsymbol{H})^{-1}\boldsymbol{H}^T\boldsymbol{z} x∗=−(HTH)−1HTz 这里不进行赘述。
实际的问题中,我们通常要最小化不止一个残差,不同残差通常会按其重要性(不确定性)分配一个相应的权重系数,且观测模型也通常是非线性的,即求解以下问题:
e i ( x ) = z i − h i ( x ) i = 1 , 2 , . . . , n ∣ ∣ e i ( x ) ∣ ∣ Σ i 2 = e i T Σ i e i x ∗ = arg min x F ( x ) = arg min x ∑ i ∣ ∣ e i ( x ) ∣ ∣ Σ i 2 \begin{aligned} \boldsymbol{e}_i(\boldsymbol{x}) &= \boldsymbol{z}_i - h_i(\boldsymbol{x}) \qquad i = 1, 2, ..., n\\ ||\boldsymbol{e}_i(\boldsymbol{x})||^2_{\Sigma_i} &= \boldsymbol{e}_i^T\boldsymbol{\Sigma}_i\boldsymbol{e}_i\\ \boldsymbol{x}^* &= \arg\min_{\boldsymbol{x}}F(\boldsymbol{x})\\ &= \arg\min_{\boldsymbol{x}}\sum_i||\boldsymbol{e}_i(\boldsymbol{x})||^2_{\Sigma_i} \end{aligned} ei(x)∣∣ei(x)∣∣Σi2x∗=zi−hi(x)i=1,2,...,n=eiTΣiei=argxminF(x)=argxmini∑∣∣ei(x)∣∣Σi2
我们想要获得一个状态量 x ∗ \boldsymbol{x}^* x∗,使得损失函数 F ( x ) F(\boldsymbol{x}) F(x) 取得局部最小值。
在具体求解之前,先考虑 F ( x ) F(\boldsymbol{x}) F(x) 的性质,对其进行二阶泰勒展开:
F ( x + Δ x ) = F ( x ) + J Δ x + 1 2 Δ x T H Δ x + O ( ∣ ∣ Δ x ∣ ∣ 3 ) F(\boldsymbol{x} + \Delta\boldsymbol{x}) = F(\boldsymbol{x}) + \boldsymbol{J}\Delta\boldsymbol{x} + \frac{1}{2}\Delta\boldsymbol{x}^T\boldsymbol{H}\Delta\boldsymbol{x} + O(||\Delta\boldsymbol{x}||^3) F(x+Δx)=F(x)+JΔx+21ΔxTHΔx+O(∣∣Δx∣∣3)
忽略高阶余项,对二次函数,有以下性质:
如果在点 x ∗ \boldsymbol{x}^* x∗ 处,导数为 0 \boldsymbol{0} 0,则这个点为稳定点,根据 Hessian 矩阵的正定性有不同性质:
- 如果 H \boldsymbol{H} H 为正定矩阵,则 F ( x ∗ ) F(\boldsymbol{x}^*) F(x∗) 为局部最小值
- 如果 H \boldsymbol{H} H 为负定矩阵,则 F ( x ∗ ) F(\boldsymbol{x}^*) F(x∗) 为局部最大值
- 如果 H \boldsymbol{H} H 为不定矩阵,则 F ( x ∗ ) F(\boldsymbol{x}^*) F(x∗) 为鞍点
在实际过程中,一般 F ( x ) F(x) F(x) 比较复杂,我们没有办法直接使其导数为 0 进而求出该点,因此常用的是迭代法,即找到一个下降方向使损失函数随 x \boldsymbol{x} x 的迭代逐渐减少,直到 x \boldsymbol{x} x 收敛到 x ∗ \boldsymbol{x}^* x∗。下面整理以下常用的几种迭代方法。
2.迭代下降法
上面提到,我们需要找到一个 x \boldsymbol{x} x 的迭代量使得 F ( x ) F(\boldsymbol{x}) F(x) 减少。这个过程分两步:
找到 F ( x ) \boldsymbol{F(x)} F(x) 的下降方向,构建该方向的单位向量 d \boldsymbol{d} d
确定该方向的迭代步长 α \alpha α
迭代后的自变量 x + α d \boldsymbol{x} + \alpha\boldsymbol{d} x+αd 对应的函数值可以用一阶泰勒展开近似(当步长足够小的时候):
F ( x + α d ) = F ( x ) + α J d F(\boldsymbol{x} + \alpha\boldsymbol{d}) = F(\boldsymbol{x}) + \alpha\boldsymbol{Jd} F(x+αd)=F(x)+αJd
因此,不难发现,要保持 F ( x ) F(x) F(x) 是下降的,只需要保证 J d < 0 \boldsymbol{Jd} < 0 Jd<0。以下几种方法都是以不同思路在寻找一个合适的方向进行迭代。
3.最速下降法
基于上一部分,我们知道变化量为 α J d \alpha\boldsymbol{Jd} αJd,其中 J d = ∣ ∣ J ∣ ∣ cos θ \boldsymbol{Jd} = ||\boldsymbol{J}||\cos{\theta} Jd=∣∣J∣∣cosθ, θ \theta θ 为梯度 J \boldsymbol{J} J 和 d \boldsymbol{d} d 的夹角。当 θ = − π \theta = -\pi θ=−π 时, J d = − ∣ ∣ J ∣ ∣ \boldsymbol{Jd} = -||\boldsymbol{J}|| Jd=−∣∣J∣∣ 取得最小值,此时方向向量为:
d = − J T ∣ ∣ J ∣ ∣ \boldsymbol{d} = \frac{-\boldsymbol{J}^T}{||\boldsymbol{J}||} d=∣∣J∣∣−JT
因此,沿梯度 J \boldsymbol{J} J 的负方向可以使 F ( x ) F(\boldsymbol{x}) F(x),但实际过程中,一般只会在迭代刚开始使用这种方法,当接近最优值时这种方法会出现震荡并且收敛较慢。
4.牛顿法
对 F ( x ) F(\boldsymbol{x}) F(x) 进行二阶泰勒展开有:
F ( x + Δ x ) = F ( x ) + J Δ x + 1 2 Δ x T H Δ x F(\boldsymbol{x} + \Delta\boldsymbol{x}) = F(\boldsymbol{x}) + \boldsymbol{J}\Delta\boldsymbol{x} + \frac{1}{2}\Delta\boldsymbol{x}^T\boldsymbol{H}\Delta\boldsymbol{x} F(x+Δx)=F(x)+JΔx+21ΔxTHΔx
我们关注的是求一个 Δ x \Delta\boldsymbol{x} Δx 使得 J Δ x + 1 2 Δ x T H Δ x \boldsymbol{J}\Delta\boldsymbol{x} + \frac{1}{2}\Delta\boldsymbol{x}^T\boldsymbol{H}\Delta\boldsymbol{x} JΔx+21ΔxTHΔx 最小,因此可以求导得:
∂ ( J Δ x + 1 2 Δ x T H Δ x ) ∂ Δ x = J T + H Δ x = 0 ⇒ Δ x = − H − 1 J T \begin{aligned} \frac{\partial(\boldsymbol{J}\Delta\boldsymbol{x} + \frac{1}{2}\Delta\boldsymbol{x}^T\boldsymbol{H}\Delta\boldsymbol{x})}{\partial\Delta\boldsymbol{x}} &= \boldsymbol{J}^T + \boldsymbol{H}\Delta\boldsymbol{x} = 0\\ \Rightarrow \Delta\boldsymbol{x} &= -\boldsymbol{H}^{-1}\boldsymbol{J}^T \end{aligned} ∂Δx∂(JΔx+21ΔxTHΔx)⇒Δx=JT+HΔx=0=−H−1JT
当 H \boldsymbol{H} H 为正定矩阵且当前 x \boldsymbol{x} x 在最优点附近时,取 Δ x = − H − 1 J T \Delta\boldsymbol{x} = -\boldsymbol{H}^{-1}\boldsymbol{J}^T Δx=−H−1JT 可以使函数获得局部最小值。但缺点是残差的 Hessian 函数通常比较难求。
5.阻尼法
在牛顿法的基础上,为了控制每次迭代不要太激进,我们可以在损失函数中增加一项惩罚项,如下所示:
arg min Δ x { F ( x ) + J Δ x + 1 2 Δ x T H Δ x + 1 2 μ ( Δ x ) T ( Δ x ) } \arg\min_{\Delta\boldsymbol{x}}\left\{F(\boldsymbol{x}) + \boldsymbol{J}\Delta\boldsymbol{x} + \frac{1}{2}\Delta\boldsymbol{x}^T\boldsymbol{H}\Delta\boldsymbol{x} + \frac{1}{2}\mu(\Delta\boldsymbol{x})^T(\Delta\boldsymbol{x})\right\} argΔxmin{F(x)+JΔx+21ΔxTHΔx+21μ(Δx)T(Δx)}
当我们选的 Δ x \Delta\boldsymbol{x} Δx 太大时,损失函数也会变大,变大的幅度由 μ \mu μ 决定,因此我们可以控制每次迭代量 Δ x \Delta\boldsymbol{x} Δx 的大小。同样在右侧部分对 Δ x \Delta\boldsymbol{x} Δx 求导有:
J T + H Δ x + μ Δ x = 0 ( H + μ I ) Δ x = − J T \begin{aligned} \boldsymbol{J}^T + \boldsymbol{H}\Delta\boldsymbol{x} + \mu\Delta\boldsymbol{x} &= 0\\ (\boldsymbol{H} + \mu\boldsymbol{I})\Delta\boldsymbol{x} = -\boldsymbol{J}^T \end{aligned} JT+HΔx+μΔx(H+μI)Δx=−JT=0
这个思路我们后面在介绍 LM 法时也会用到。
6.高斯牛顿(GN)法
在前面的整理中实际上我们求解的是一系列残差的和,求单个残差的雅可比比较简单,因此在后续的几种方法中我们关注各个残差的变化。将上述非线性最小二乘问题中的各个残差写成向量形式:
F ( x ) = E ( x ) = [ e 1 ( x ) e 2 ( x ) . . . e n ( x ) ] \boldsymbol{F}(\boldsymbol{x}) =\boldsymbol{E}(\boldsymbol{x}) =\begin{bmatrix} \boldsymbol{e}_1(\boldsymbol{x})\\ \boldsymbol{e}_2(\boldsymbol{x})\\ ...\\ \boldsymbol{e}_n(\boldsymbol{x})\\ \end{bmatrix} F(x)=E(x)= e1(x)e2(x)...en(x)
对 e ( x ) \boldsymbol{e}(\boldsymbol{x}) e(x) 进行泰勒展开,有:
e ( x + Δ x ) = e ( x ) + J Δ x \boldsymbol{e}(\boldsymbol{x} + \Delta\boldsymbol{x}) = \boldsymbol{e}(\boldsymbol{x}) + \boldsymbol{J}\Delta\boldsymbol{x} e(x+Δx)=e(x)+JΔx
上式中, J \boldsymbol{J} J 是残差矩阵 e ( x ) \boldsymbol{e}(\boldsymbol{x}) e(x) 对状态量的雅可比矩阵。
注意到在原来的线性最小二乘问题中,对每个残差还有一个权重矩阵 Σ \boldsymbol{\Sigma} Σ。这种情况下,我们只需要令 e i ( x ) = Σ i e i ( x ) \boldsymbol{e}_i(\boldsymbol{x}) = \sqrt{\boldsymbol{\Sigma}_i}\boldsymbol{e}_i(\boldsymbol{x}) ei(x)=Σiei(x) 即可。因此下式中暂不考虑 Σ \boldsymbol{\Sigma} Σ 的影响。
在这种形式下对 e ( x ) \boldsymbol{e}(\boldsymbol{x}) e(x) 进行泰勒展开,有:
∣ ∣ e ( x + Δ x ) ∣ ∣ 2 = e ( x + Δ x ) T e ( x + Δ x ) = ( e ( x ) + J Δ x ) T ( e ( x ) + J Δ x ) = e ( x ) T e ( x ) + Δ x T J T e ( x ) + e ( x ) T J Δ x + Δ x T J T J Δ x \begin{aligned} ||e(\boldsymbol{x} + \Delta\boldsymbol{x}) ||^2&= \boldsymbol{e}(\boldsymbol{x} + \Delta\boldsymbol{x})^T\boldsymbol{e}(\boldsymbol{x} + \Delta\boldsymbol{x})\\ &= (\boldsymbol{e}(\boldsymbol{x}) + \boldsymbol{J}\Delta\boldsymbol{x})^T(\boldsymbol{e}(\boldsymbol{x}) + \boldsymbol{J}\Delta\boldsymbol{x})\\ &= \boldsymbol{e}(\boldsymbol{x})^T\boldsymbol{e}(\boldsymbol{x}) + \Delta\boldsymbol{x}^T\boldsymbol{J}^T\boldsymbol{e}(\boldsymbol{x}) + \boldsymbol{e}(\boldsymbol{x})^T\boldsymbol{J}\Delta\boldsymbol{x} + \Delta\boldsymbol{x}^T\boldsymbol{J}^T\boldsymbol{J}\Delta\boldsymbol{x} \end{aligned} ∣∣e(x+Δx)∣∣2=e(x+Δx)Te(x+Δx)=(e(x)+JΔx)T(e(x)+JΔx)=e(x)Te(x)+ΔxTJTe(x)+e(x)TJΔx+ΔxTJTJΔx
上式中,注意到: e ( x ) e(\boldsymbol{x}) e(x) 是一维的,因此 Δ x T J T e ( x ) = e ( x ) T J Δ x \Delta\boldsymbol{x}^T\boldsymbol{J}^T\boldsymbol{e}(\boldsymbol{x}) = \boldsymbol{e}(\boldsymbol{x})^T\boldsymbol{J}\Delta\boldsymbol{x} ΔxTJTe(x)=e(x)TJΔx,因此化简得:
F ( x + Δ x ) = e ( x ) T e ( x ) + 2 e ( x ) T J Δ x + Δ x T J T J Δ x = F ( x ) + 2 e ( x ) T J Δ x + Δ x T J T J Δ x \begin{aligned} F(\boldsymbol{x} + \Delta\boldsymbol{x}) &= \boldsymbol{e}(\boldsymbol{x})^T\boldsymbol{e}(\boldsymbol{x}) + 2\boldsymbol{e}(\boldsymbol{x})^T\boldsymbol{J}\Delta\boldsymbol{x} + \Delta\boldsymbol{x}^T\boldsymbol{J}^T\boldsymbol{J}\Delta\boldsymbol{x}\\ &= F(\boldsymbol{x}) + 2\boldsymbol{e}(\boldsymbol{x})^T\boldsymbol{J}\Delta\boldsymbol{x} + \Delta\boldsymbol{x}^T\boldsymbol{J}^T\boldsymbol{J}\Delta\boldsymbol{x} \end{aligned} F(x+Δx)=e(x)Te(x)+2e(x)TJΔx+ΔxTJTJΔx=F(x)+2e(x)TJΔx+ΔxTJTJΔx
通过这种方式,我们同样将其近似一个二次函数,并且和我们之前展开的结果比较,不难发现在这里我们实际上是用 J T e \boldsymbol{J}^T\boldsymbol{e} JTe 来近似 Jacobian 矩阵,用 J T J \boldsymbol{J}^T\boldsymbol{J} JTJ 来近似 Hessian 矩阵。因此,当 J \boldsymbol{J} J 满秩时,我们可以保证在上式导数为 0 的地方可以确保函数取得局部最小值。同样,在上式右侧部分对 Δ x \Delta\boldsymbol{x} Δx 求导并使其为 0 有:
J T e ( x ) + J T J Δ x = 0 ⇒ J T J Δ x = − J T e ( x ) ⇒ H Δ x = b \begin{aligned} \boldsymbol{J}^T\boldsymbol{e}(\boldsymbol{x}) + \boldsymbol{J}^T\boldsymbol{J}\Delta\boldsymbol{x} = 0\\ \Rightarrow \boldsymbol{J}^T\boldsymbol{J}\Delta\boldsymbol{x} &= -\boldsymbol{J}^T\boldsymbol{e}(\boldsymbol{x})\\ \Rightarrow \boldsymbol{H}\Delta\boldsymbol{x} &= \boldsymbol{b} \end{aligned} JTe(x)+JTJΔx=0⇒JTJΔx⇒HΔx=−JTe(x)=b
上式中,我们令 H = J T J , b = − J T e \boldsymbol{H} = \boldsymbol{J}^T\boldsymbol{J}, \boldsymbol{b} = -\boldsymbol{J}^T\boldsymbol{e} H=JTJ,b=−JTe。这样我们获得了高斯牛顿法的求解过程:
- 计算残差矩阵关于状态值的雅可比矩阵 J \boldsymbol{J} J
- 利用雅可比矩阵和残差构建信息矩阵和信息向量 H , b \boldsymbol{H}, \boldsymbol{b} H,b
- 计算当次迭代量: Δ x = H − 1 b \Delta\boldsymbol{x} = \boldsymbol{H}^{-1}\boldsymbol{b} Δx=H−1b
- 如果迭代量足够小则结束迭代,否则进入下一次迭代
7.莱文贝格马夸特(LM)法
LM 法是在高斯牛顿法的基础上按照阻尼法的思路加入阻尼因子,即求解以下方程:
( H + μ I ) Δ x = b (\boldsymbol{H} + \mu\boldsymbol{I})\Delta\boldsymbol{x} = \boldsymbol{b} (H+μI)Δx=b
上式中,阻尼因子的作用有:
-
添加进 H \boldsymbol{H} H 保证 H \boldsymbol{H} H 是正定的
-
当 μ \mu μ 很大时, Δ x = − ( H + μ I ) − 1 b ≈ − 1 μ b = − 1 μ J T E ( x ) \Delta\boldsymbol{x} = -(\boldsymbol{H}+\mu\boldsymbol{I})^{-1}\boldsymbol{b}\approx-\frac{1}{\mu}\boldsymbol{b}=-\frac{1}{\mu}\boldsymbol{J}^T\boldsymbol{E}(\boldsymbol{x}) Δx=−(H+μI)−1b≈−μ1b=−μ1JTE(x),接近最速下降法
-
当 μ \mu μ 很小时,则接近高斯牛顿法
因此,合理的设置阻尼因子,能够达到动态对迭代速度进行调节。阻尼因子的设置分为两部分: -
初始值的选取
-
随迭代量变化的更新策略
先来看初始值选取方法,阻尼因子的大小应该根据 J T J \boldsymbol{J}^T\boldsymbol{J} JTJ 的大小来选取,对 J T J \boldsymbol{J}^T\boldsymbol{J} JTJ 进行特征值分解,有: J T J = V Λ V T \boldsymbol{J}^T\boldsymbol{J} = \boldsymbol{V}\boldsymbol{\Lambda}\boldsymbol{V}^T JTJ=VΛVT, Λ = diag ( λ 1 , λ 2 , . . . , λ n ) , V = [ v 1 , . . . , v n ] \boldsymbol{\Lambda} = \text{diag}(\lambda_1, \lambda_2,..., \lambda_n), \boldsymbol{V} = [\boldsymbol{v}_1, ..., \boldsymbol{v}_n] Λ=diag(λ1,λ2,...,λn),V=[v1,...,vn],因此,迭代公式化简为:
( V Λ V T + μ I ) Δ x = b Δ x = ( V Λ V T + μ I ) − 1 b = − ∑ i v i T b λ i + μ v i \begin{aligned} (\boldsymbol{V\Lambda}\boldsymbol{V}^T + \mu\boldsymbol{I})\Delta\boldsymbol{x} &= \boldsymbol{b}\\ \Delta\boldsymbol{x} &= (\boldsymbol{V\Lambda}\boldsymbol{V}^T + \mu\boldsymbol{I})^{-1}\boldsymbol{b}\\ &= -\sum_i\frac{\boldsymbol{v}_i^T\boldsymbol{b}}{\lambda_i + \mu}\boldsymbol{v}_i \end{aligned} (VΛVT+μI)ΔxΔx=b=(VΛVT+μI)−1b=−i∑λi+μviTbvi
因此,将 μ \mu μ 选为 λ i \lambda_i λi 接近即可,一个简单的思路是设 μ 0 = τ max ( J T J ) i i \mu_0 = \tau\max{(\boldsymbol{J}^T\boldsymbol{J})_{ii}} μ0=τmax(JTJ)ii,实际中一般设 τ ≈ [ 1 0 − 8 , 1 ] \tau \approx [10^{-8}, 1] τ≈[10−8,1]
接下来看 μ \mu μ 的更新策略,先定性分析应该怎么更新阻尼因子:
- 当 Δ x \Delta\boldsymbol{x} Δx 令 F ( x ) F(\boldsymbol{x}) F(x) 增加时,应该提高 μ \mu μ 来降低 Δ x \Delta\boldsymbol{x} Δx 即通过减少步长来降低本次迭代带来的影响
- 当 Δ x \Delta\boldsymbol{x} Δx 令 F ( x ) F(\boldsymbol{x}) F(x) 减少时,应该降低 μ \mu μ 来提高 Δ x \Delta\boldsymbol{x} Δx 即通过增加步长来提高这次迭代的影响
下面进行定量分析,令 L ( Δ x ) = F ( x ) + 2 E ( x ) T J Δ x + 1 2 Δ x T J T J Δ x L(\Delta\boldsymbol{x}) = F(\boldsymbol{x}) +2\boldsymbol{E}(\boldsymbol{x})^T\boldsymbol{J}\Delta\boldsymbol{x} + \frac{1}{2}\Delta\boldsymbol{x}^T\boldsymbol{J}^T\boldsymbol{J}\Delta\boldsymbol{x} L(Δx)=F(x)+2E(x)TJΔx+21ΔxTJTJΔx考虑以下比例因子:
ρ = F ( x ) − F ( x + Δ x ) L ( 0 ) − F ( Δ x ) \rho = \frac{F(\boldsymbol{x}) - F(\boldsymbol{x} + \Delta\boldsymbol{x})}{L(\boldsymbol{0}) - F(\Delta\boldsymbol{x})} ρ=L(0)−F(Δx)F(x)−F(x+Δx)
Marquardt 提出一个策略:
- 当 ρ < 0 \rho < 0 ρ<0,表示当前 Δ x \Delta\boldsymbol{x} Δx 使 F ( x ) F(\boldsymbol{x}) F(x) 增大,表示离最优值还很远,应该提高 μ \mu μ 使其接近最速下降法进行较大幅度的更新
- 当 ρ > 0 \rho > 0 ρ>0 且比较大,表示当前 Δ x \Delta\boldsymbol{x} Δx 使 F ( x ) F(\boldsymbol{x}) F(x) 减小,应该降低 μ \mu μ 使其接近高斯牛顿法,降低速度更新至最优点
- 如果 ρ > 0 \rho > 0 ρ>0 但比较小,表示已经到最优点附近,则增大阻尼 μ \mu μ,缩小迭代步长
Marquardt 的具体策略如下:
if rho < 0.25: mu = mu * 2
else if rho > 0.75: mu = mu /3
一个使用 Marquardt 策略进行更新的过程如下:

可以发现,效果并不算很好,随着迭代次数的增加, μ \mu μ 开始进行震荡,表示迭代量周期性的使 F ( x ) F(\boldsymbol{x}) F(x) 增加又下降。
因此,Nielsen 提出了另一个策略,也是 G2O 和 Ceres 中使用的策略:
if rho > 0:mu = mu * max(1/3, 1 - (2 * rho - 1)^3)v = 2
else:mu = mu * vv = 2 * v
使用这种策略进行优化的例子如下:
可以看到, μ \mu μ 随着迭代的进行可以比较平滑的持续下降直至达到收敛。

8.鲁棒核函数
在进行最小二乘问题中,我们会遇到一些异常观测值使得观测残差特别大,如果不对这些异常点做处理会影响在优化过程中,优化器会尝试最小化异常的残差项,最后影响状态估计的精度,鲁棒核函数就是用来降低这些异常观测值造成的影响。
将鲁棒核函数直接作用在每个残差项上,将最小二乘问题变成如下形式:
F ( x ) = ∑ i ρ ( ∣ ∣ e i ( x ) ∣ ∣ 2 ) F(\boldsymbol{x}) = \sum_i\rho(||e_i(\boldsymbol{x})||^2) F(x)=i∑ρ(∣∣ei(x)∣∣2)
使用鲁棒核函数时求解非线性最小二乘的过程
在这个形式下对带有鲁棒核函数的残差进行二阶泰勒展开:
ρ ( s + Δ s ) = ρ ( x ) + ρ ′ ( x ) Δ s + 1 2 ρ ′ ′ ( x ) Δ 2 s \rho(s + \Delta s) = \rho(x) + \rho'(x)\Delta s + \frac{1}{2}\rho''(x)\Delta^2s ρ(s+Δs)=ρ(x)+ρ′(x)Δs+21ρ′′(x)Δ2s
上式中,变化量 Δ s \Delta s Δs 的计算方式如下:
Δ s k = ∣ ∣ e i ( x + Δ x ) ∣ ∣ 2 − ∣ ∣ e i ( x ) ∣ ∣ 2 = ∣ ∣ e i ( x ) + J i Δ x ∣ ∣ 2 − ∣ ∣ e i ( x ) ∣ ∣ 2 = 2 e i ( x ) T J i Δ x + Δ x T J i T J i Δ x \begin{aligned} \Delta s_k &= ||e_i(\boldsymbol{x}+\Delta\boldsymbol{x})||^2 - ||e_i(\boldsymbol{x})||^2\\ &= ||e_i(\boldsymbol{x})+\boldsymbol{J}_i\Delta\boldsymbol{x}||^2 - ||e_i(\boldsymbol{x})||^2\\ &= 2e_i(\boldsymbol{x})^T\boldsymbol{J}_i\Delta\boldsymbol{x}+\Delta\boldsymbol{x}^T\boldsymbol{J}_i^T\boldsymbol{J}_i\Delta\boldsymbol{x} \end{aligned} Δsk=∣∣ei(x+Δx)∣∣2−∣∣ei(x)∣∣2=∣∣ei(x)+JiΔx∣∣2−∣∣ei(x)∣∣2=2ei(x)TJiΔx+ΔxTJiTJiΔx
将 Δ s \Delta s Δs 代入 ρ ( s + Δ s ) \rho(s + \Delta s) ρ(s+Δs) 可得:
ρ ( s + Δ s ) = ρ ( s ) + ρ ′ ( s ) ( 2 e i ( x ) T J i Δ x + Δ x T J i T J i Δ x ) + 1 2 ρ ′ ′ ( s ) ( 2 e i ( x ) T J i Δ x + Δ x T J i T J i Δ x ) 2 ≈ ρ ( s ) + 2 ρ ′ ( s ) e i ( x ) T J i Δ x + ρ ′ ( s ) Δ x T J i T J i Δ x + 2 ρ ′ ′ ( s ) Δ x T J i T e i ( x ) e i ( x ) T J i Δ x \begin{aligned} \rho(s + \Delta s) =& \rho(s) + \rho'(s)(2e_i(\boldsymbol{x})^T\boldsymbol{J}_i\Delta\boldsymbol{x}+\Delta\boldsymbol{x}^T\boldsymbol{J}_i^T\boldsymbol{J}_i\Delta\boldsymbol{x}) \\ &+ \frac{1}{2}\rho''(s)(2e_i(\boldsymbol{x})^T\boldsymbol{J}_i\Delta\boldsymbol{x}+\Delta\boldsymbol{x}^T\boldsymbol{J}_i^T\boldsymbol{J}_i\Delta\boldsymbol{x})^2\\ \approx& \rho(s) + 2\rho'(s)e_i(\boldsymbol{x})^T\boldsymbol{J}_i\Delta\boldsymbol{x}+\rho'(s)\Delta\boldsymbol{x}^T\boldsymbol{J}_i^T\boldsymbol{J}_i\Delta\boldsymbol{x} \\ &+ 2\rho''(s)\Delta\boldsymbol{x}^T\boldsymbol{J}_i^Te_i(\boldsymbol{x})e_i(\boldsymbol{x})^T\boldsymbol{J}_i\Delta\boldsymbol{x} \end{aligned} ρ(s+Δs)=≈ρ(s)+ρ′(s)(2ei(x)TJiΔx+ΔxTJiTJiΔx)+21ρ′′(s)(2ei(x)TJiΔx+ΔxTJiTJiΔx)2ρ(s)+2ρ′(s)ei(x)TJiΔx+ρ′(s)ΔxTJiTJiΔx+2ρ′′(s)ΔxTJiTei(x)ei(x)TJiΔx
按照之前的思路,对上式求导并使其为 0,可得:
∑ i J i T ( ρ ′ ( s ) + 2 ρ ′ ′ ( s ) e i ( x ) e i ( x ) T ) J Δ x = − ∑ i ρ ′ ( s ) J i T e i ( x ) \sum_i\boldsymbol{J}_i^T(\rho'(s) + 2\rho''(s)e_i(\boldsymbol{\boldsymbol{x}})e_i(\boldsymbol{x})^T)\boldsymbol{J}\Delta\boldsymbol{x} = -\sum_i\rho'(s)\boldsymbol{J}_i^Te_i(\boldsymbol{x}) i∑JiT(ρ′(s)+2ρ′′(s)ei(x)ei(x)T)JΔx=−i∑ρ′(s)JiTei(x)
对比之前的矩阵 J T J Δ x = − J i T e ( x ) \boldsymbol{J}^T\boldsymbol{J}\Delta\boldsymbol{x} = -\boldsymbol{J}_i^T\boldsymbol{e}(\boldsymbol{x}) JTJΔx=−JiTe(x) 可得,当我们使用了鲁棒核函数之后,只需要将各项残差的核函数的一阶二阶导数值计算出,再按照以上形式对信息矩阵和信息向量进行更新即可。
常用的鲁棒核函数
柯西鲁棒核函数:
ρ ( s ) = c 2 log ( 1 + s c 2 ) ρ ′ ( s ) = 1 1 + s c 2 ρ ′ ′ ( s ) = − 1 c 2 ( ρ ′ ( s ) ) 2 \begin{aligned} \rho(s) &= c^2\log{(1+\frac{s}{c^2})}\\ \rho'(s) &= \frac{1}{1+\frac{s}{c^2}}\\ \rho''(s) &= -\frac{1}{c^2}(\rho'(s))^2 \end{aligned} ρ(s)ρ′(s)ρ′′(s)=c2log(1+c2s)=1+c2s1=−c21(ρ′(s))2
其中, c c c 为控制参数。当残差是正态分布,Huber c 选为 1.345,Cauchy c 选为 2.3849。不同鲁棒核函数的效果如下图所示:

相关文章:

最小二乘问题和非线性优化
最小二乘问题和非线性优化 0.引言1.最小二乘问题2.迭代下降法3.最速下降法4.牛顿法5.阻尼法6.高斯牛顿(GN)法7.莱文贝格马夸特(LM)法8.鲁棒核函数 0.引言 转载自此处,修正了一点小错误。 1.最小二乘问题 在求解 SLAM 中的最优状态估计问题时,我们一般…...

Selenium/webdriver原理解析
最近在看一些底层的东西。driver翻译过来是驱动,司机的意思。如果将webdriver比做成司机,竟然非常恰当。 我们可以把WebDriver驱动浏览器类比成出租车司机开出租车。在开出租车时有三个角色: 乘客:他/她告诉出租车司机去哪里&…...
多用户跨境B2B2C商城后台管理系统快速搭建
搭建一个多用户跨境B2B2C商城后台管理系统需要考虑多个方面,包括系统架构设计、用户权限管理、商品管理、订单管理、支付管理、物流管理等。搭建步骤如下: 1. 系统架构设计 首先,需要设计一个稳定可靠的系统架构。选择一个适合B2B2C商城的商…...

MySQL 优化
问题描述 MySQL 的性能优化分为四个部分: 硬件和操作系统层面的优化架构设计层面的优化MySQL 程序配置优SQL 优化 一、硬件及操作系统层面优化 从硬件层面来说,影响 Mysql 性能的因素有,CPU、可用内存大小、磁盘读写速度、 网络带宽。 从操作…...

VMware Workstation及CentOS-7虚机安装
创建新的虚机: 选择安装软件(这里选的是桌面版,也可以根据实际情况进行选择) 等待检查软件依赖关系 选择安装位置,自主配置分区 创建一个普通用户 安装完成后重启 点击完成配置,进入登陆界面…...
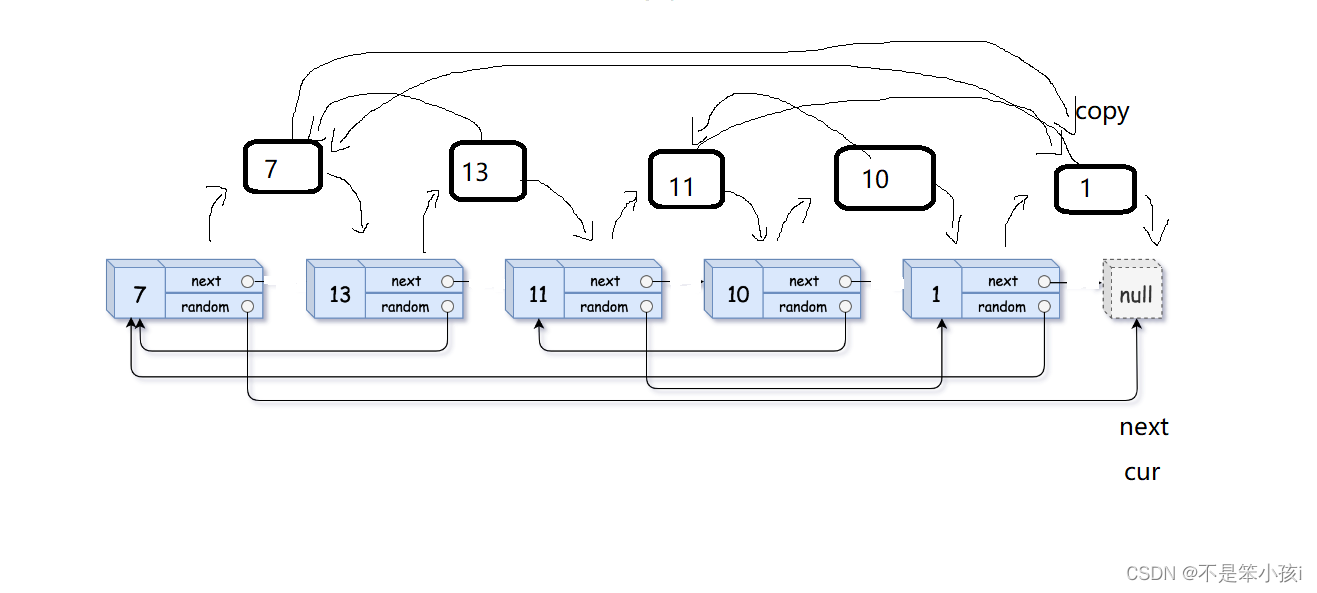
双向带头循环链表+OJ题讲解
💓博主个人主页:不是笨小孩👀 ⏩专栏分类:数据结构与算法👀 刷题专栏👀 C语言👀 🚚代码仓库:笨小孩的代码库👀 ⏩社区:不是笨小孩👀 🌹欢迎大家三连关注&…...

电脑开不了机如何解锁BitLocker硬盘锁
事情从这里说起,不想看直接跳过 早上闲着无聊,闲着没事干,将win11的用户名称改成了含有中文字符的用户名,然后恐怖的事情发生了,蓝屏了… 然后就是蓝屏收集错误信息,重启,蓝屏收集错误信息&…...
Python Web开发 Jinja2模板引擎
在之前的文章中,简单介绍了Python Web开发框架Flask,知道了如何写个Hello World,但是距离用Flask开发真正的项目,还有段距离,现在我们目标更靠近一些 —— 学习下Jinja2模板。 模板的作用 模板是用来做什么的呢&…...
ubuntu上安装mosquitto服务
1、mosquitto是什么 Mosquitto 项目最初由 IBM 和 Eurotech 于 2013 年开发,后来于 2016 年捐赠给 Eclipse 基金会。Eclipse Mosquitto 基于 Eclipse 公共许可证(EPL/EDL license)发布,用户可以免费使用。作为全球使用最广的 MQTT 协议实现之一 &#x…...

嵌入式开发学习(STC51-9-led点阵)
内容 点亮一个点; 显示数字; 显示图像; LED点阵简介 LED 点阵是由发光二极管排列组成的显示器件 通常应用较多的是8 * 8点阵,然后使用多个8 * 8点阵可组成不同分辨率的LED点阵显示屏,比如16 * 16点阵可以使用4个8 *…...
用法简介并举例)
RedisTemplate.opsForZSet()用法简介并举例
RedisTemplate.opsForZSet()是RedisTemplate类提供的用于操作ZSet类型(有序集合)的方法。它可以用于对Redis中的ZSet数据结构进行各种操作,如添加成员、获取成员、删除成员等。 下面是一些常用的RedisTemplate.opsForZSet()方法及其用法示例…...

Java个人博客系统--基于Springboot的设计与实现
目录 一、项目概述 应用技术 接口实现: 数据库定义: 数据库建表: 博客表数据库相关操作: 添加项⽬公共模块 加密MD5 页面展示:http://121.41.168.121:8080/blog_login.html 项目源码:https://gitee…...
)
在jupyter中下载数据集失败及解决方法(以IMDB为例)
在IMDB数据集下载时,由于网络原因下载失败,报错如下: Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/imdb.npz ConnectionResetError Traceback (most recent call last) … Exception: URL fetch f…...

【设计模式】-工厂方法模式
工厂方法模式(Factory Method Pattern)是一种创建型设计模式,它通过定义一个用于创建对象的接口,但是将具体对象的创建推迟到子类中。这样,子类可以决定要实例化的对象类型。工厂方法模式提供了一种方式,通…...
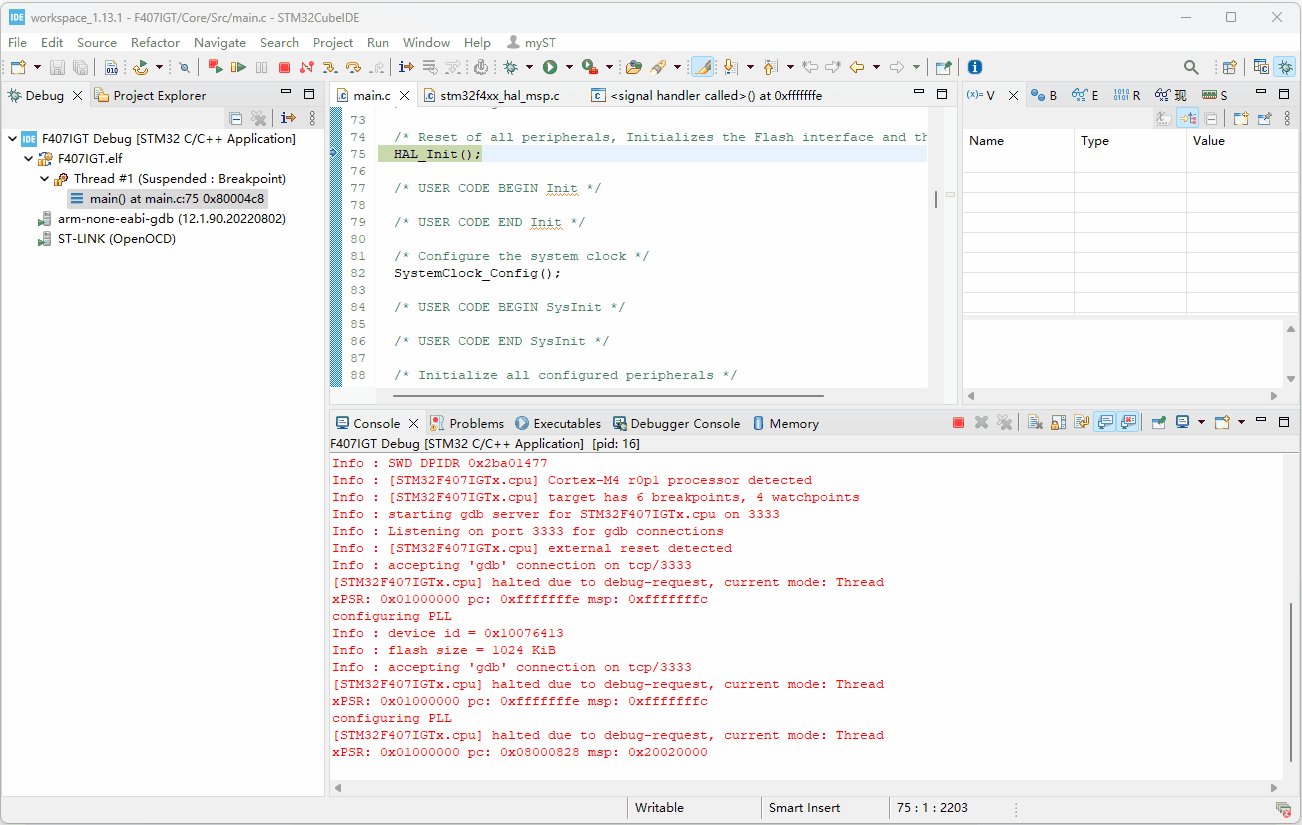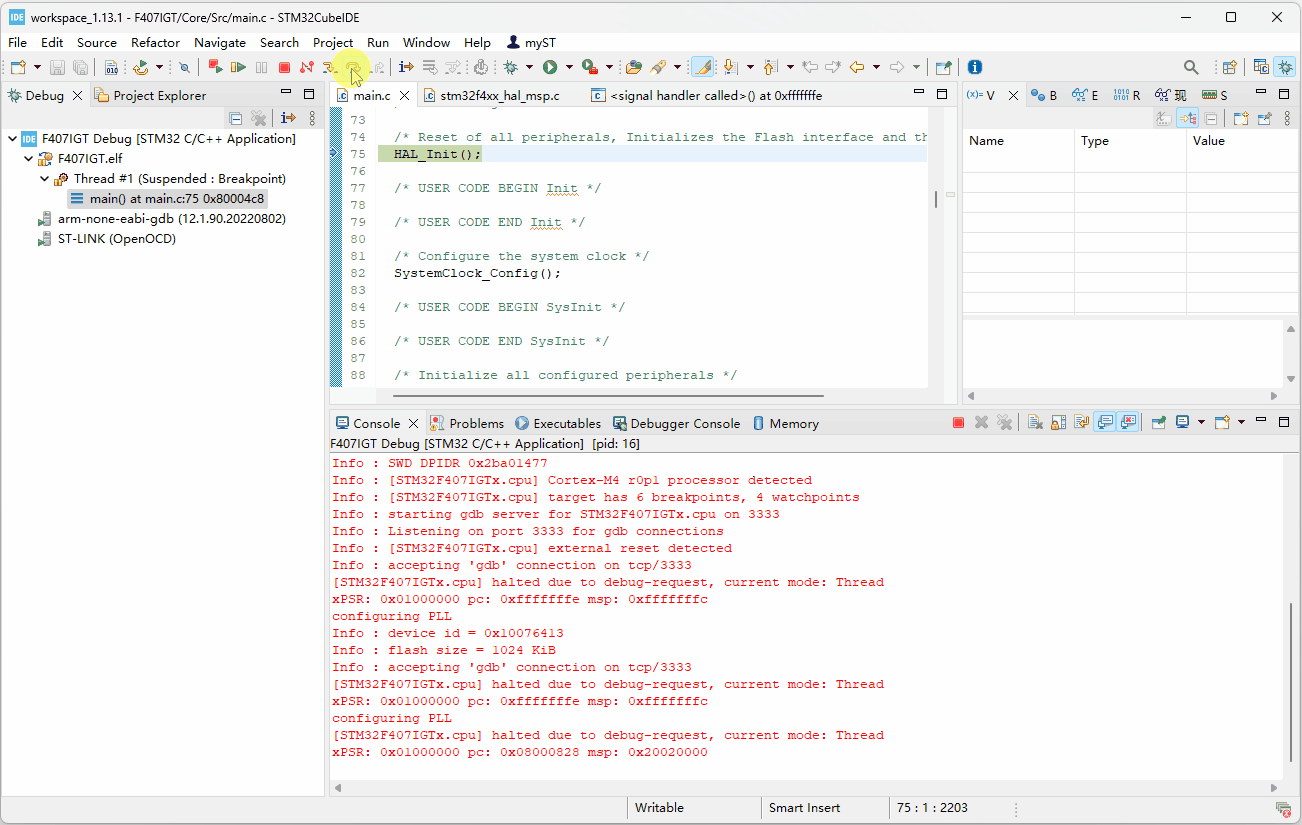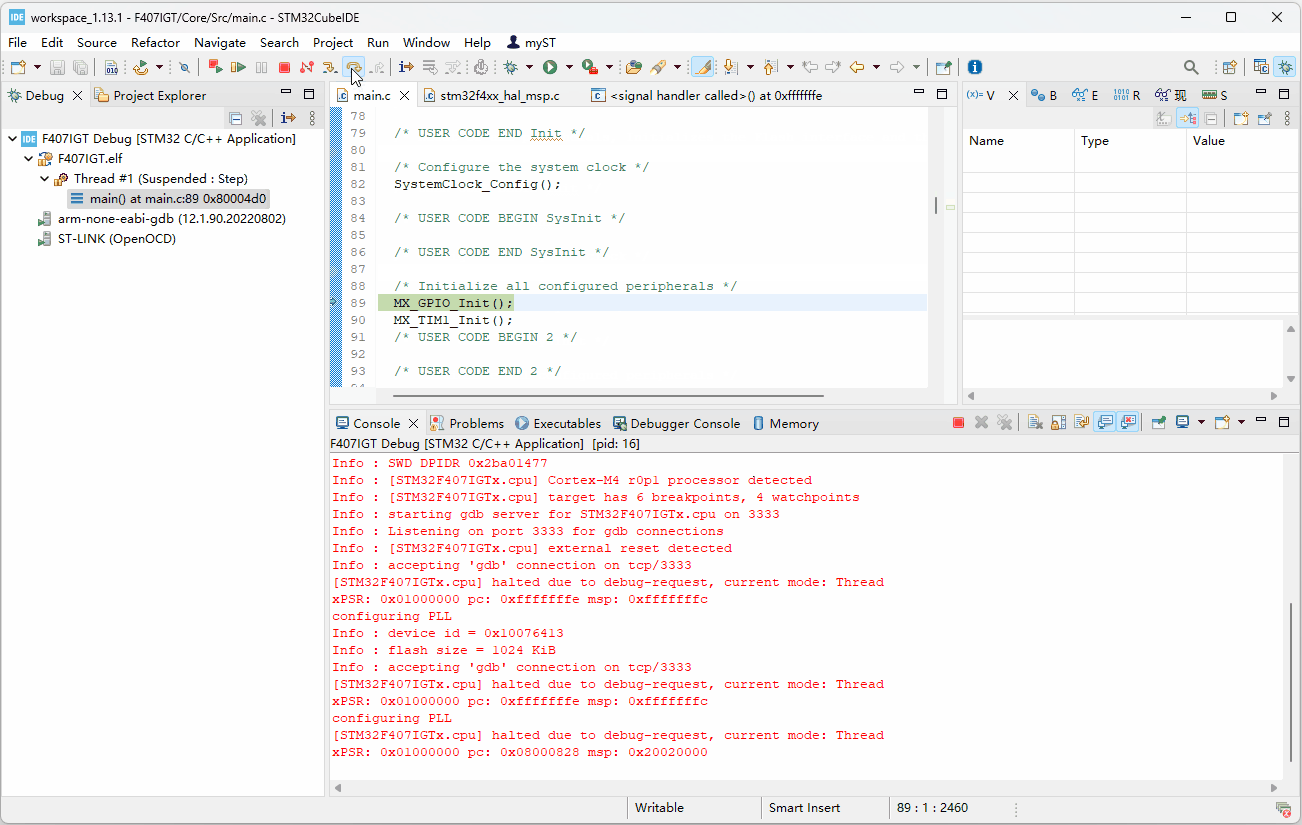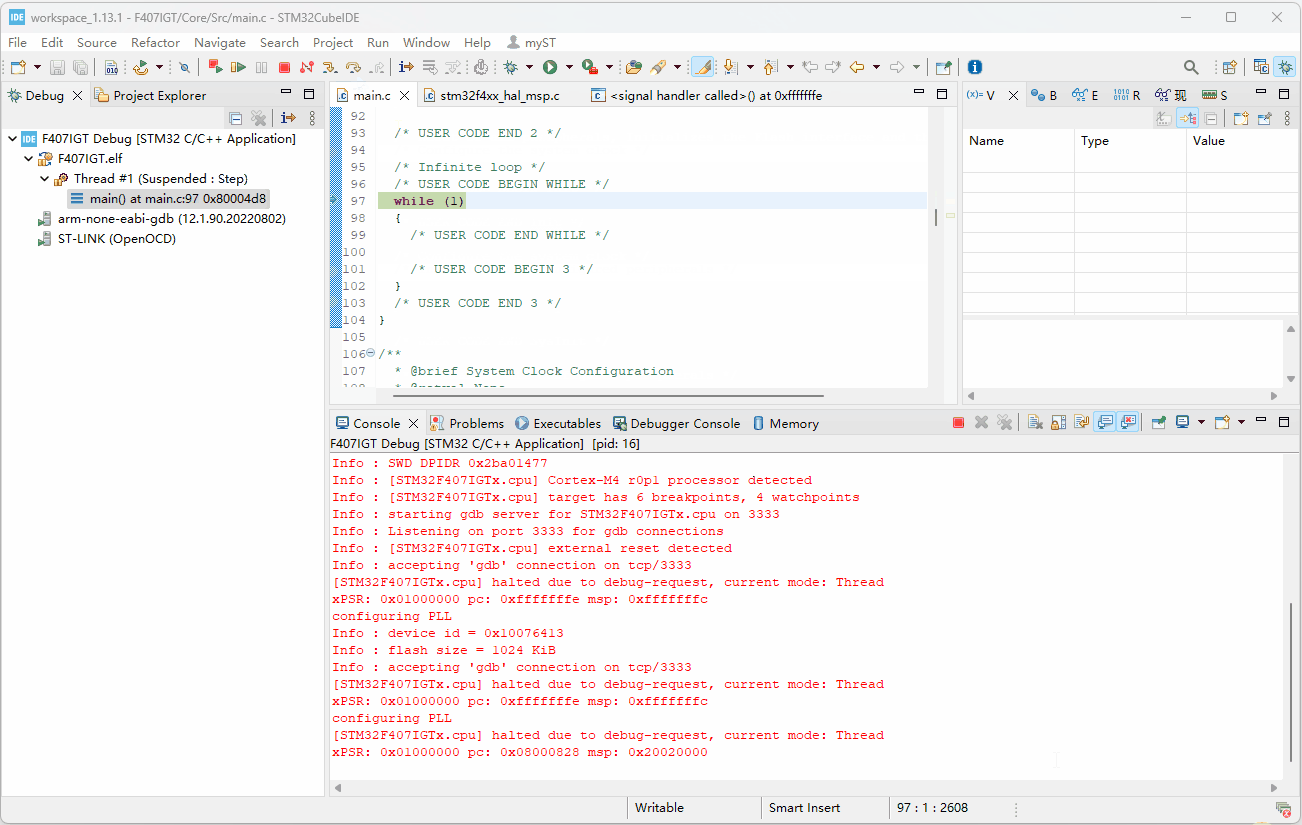
H7-TOOL的高速DAPLINK用于新版STM32CubeIDE V1.13及其以上版本的超简单实现方法(2023-08-08)
之前分享了一个方法,太繁琐了,H7-TOOL群的群友提供了一个方法,实现非常简单。1、使用STM32CubeMX或者自己创建一个STM32CubeIDE工程后,设置这两个地方即可: 配置调试器,设置完毕记得点击右下角的Apply 2、然…...
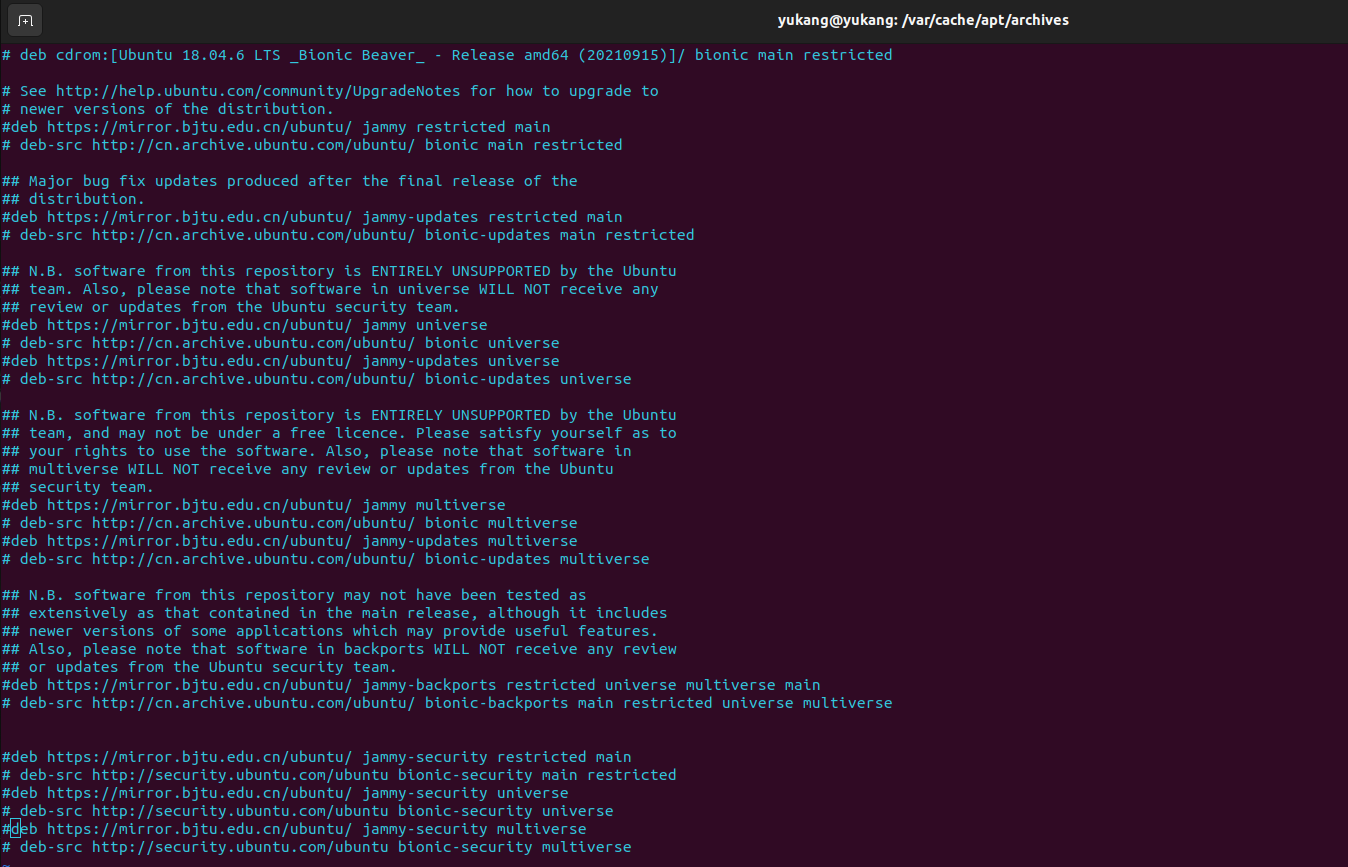
成功解决ubuntu-22.04的sudo apt-get update一直卡在【0% [Waiting for headers]】
成功解决ubuntu-22.04的sudo apt-get update一直卡在【0% [Waiting for headers]】 问题描述解决方案 问题描述 在下载安装包的时候一直卡在0% [Waiting for headers],报错信息如下: Get:1 file:/var/cudnn-local-repo-ubuntu1804-8.5.0.96 InRelease […...
:vue项目中的离线地图引入)
openLayers实战(一):vue项目中的离线地图引入
最近的项目涉及到离线地图的操作,查阅社区文章,决定使用openLayersvue离线地图的方式进行开发,前期基础引入操作完全参考掘金文章,非常优秀全面的文章。 openlayers 实战离线地图 - 掘金 此外,开发过程的地图操作可参考…...
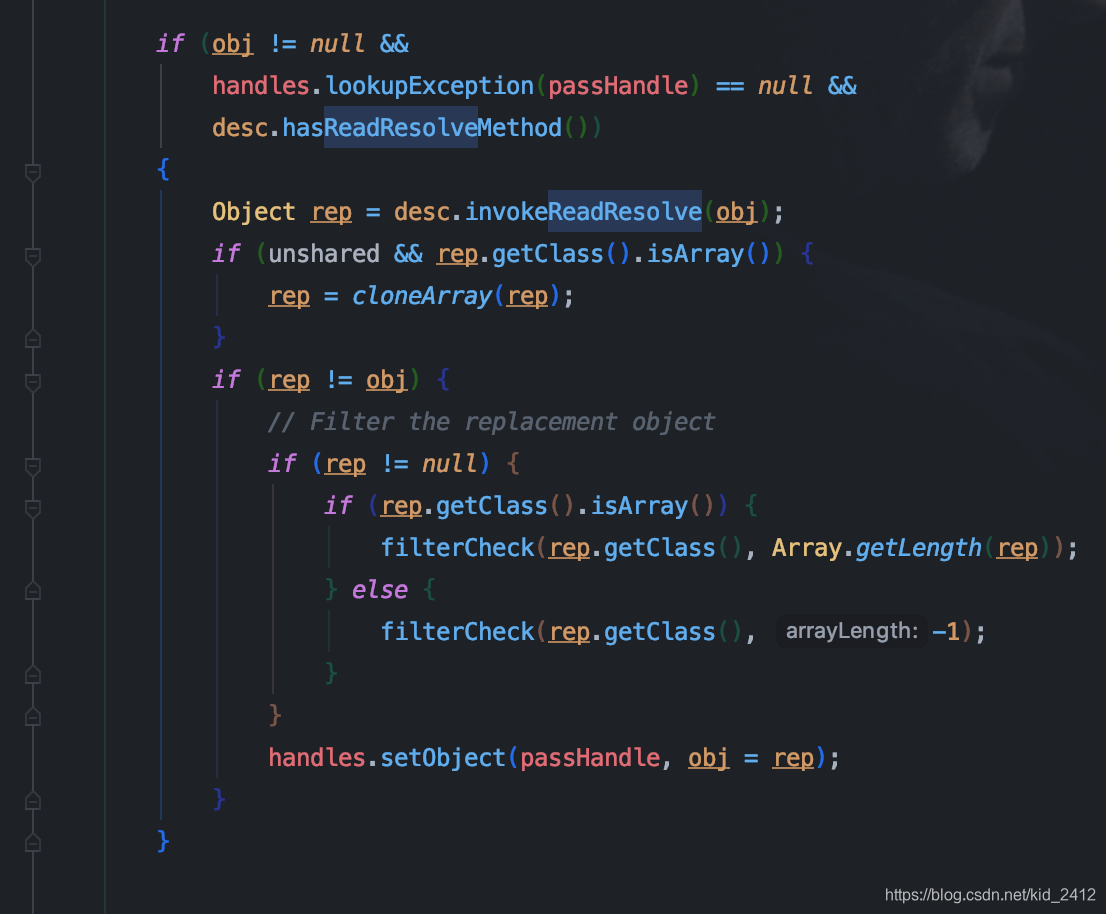
如何构造一个安全的单例?
为什么要问这个问题? 我们知道,单例是一种很常用的设计模式,主要作用就是节省系统资源,让对象在服务器中只有一份。但是实际开发中可能有很多人压根没有写过单例这种模式,只是看过或者为了面试去写写demo熟悉一下。那…...

单片机开发 esp8266
一、固件界面 二、项目介绍 固件名称:esp8266-universalboard v1.0 提供商: 半条虫(466814195) 下载:esp8266-universalboard.bin 源码地址:Gitlab...

Linux 查看版本和用户权限提升实践心得
文章目录 linux (Ubuntu内核)查看版本版本信息解释内置yum工具?用户权限提升操作步骤 查看deepin系统的版本和其debian的版本遇到的问题:deepin-release文件不存在 linux (Ubuntu内核)查看版本 使用lsb_release命令: lsb_release -a该命令将…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...
