使用动态规划实现错排问题-2023年全国青少年信息素养大赛Python复赛真题精选

[导读]:超平老师计划推出《全国青少年信息素养大赛Python编程真题解析》50讲,这是超平老师解读Python编程挑战赛真题系列的第15讲。
全国青少年信息素养大赛(原全国青少年电子信息智能创新大赛)是“世界机器人大会青少年机器人设计与信息素养大赛”赛事之一,由中国电子学会主办,包含很多赛项,大赛自2013年举办,已连续成功举办八届,已正式入围“2022-2025学年面向中小学生的全国性竞赛活动名单”。
大赛旨在激发广大青少年的科学兴趣和想象力,培养钻研探究、创新创造的科学精神和实践能力,促进青少年科技创新活动的广泛开展,发现和培养一批具有科研潜质和创新精神的青少年科技创新后备人才。
大赛主要竞赛类别包括电子科技、智能机器人、软件编程三类,全国青少年Python编程挑战赛就属于其中的软件编程类。
一.赛事说明
2023年(第9届)Python挑战赛赛程分为初赛、复赛和总决赛三个阶段。初赛是资格赛,复赛是地方选拔赛,总决赛是全国各地选拔的精英汇聚在一起进行PK。
本届Python挑战赛是在线上举行,参赛选手登录大赛官网在指定页面完成答题并提交答案。评定成绩的依据是同时考虑得分和用时两个方面,首先是得分高者名次靠前,如果得分一样,则用时少者名次靠前。
2023年全国青少年Python编程挑战赛华北赛区(北京)初中组复赛于2023年7月15日正式举行。一共有6道题,全是编程题,考试时间是90分钟。
今天超平老师分享的是第6题,也是最后一题,错排问题。
二.题目描述
题目背景:
圣诞节快到了,公司为每个员工都准备了礼物,每个礼物都有一个精美的盒子。如果所有的礼物都不小心装错了盒子,求所有礼物都装错盒子共有多少种不同情况。
输入描述:
输入一个正整数n表示公司人数,保证n ≤ 20。
输出描述:
输出一个整数,代表有多少种情况。
样例1:
输入:
2
输出:
1
三.思路分析
这是一个典型的错排问题,那什么是错排问题呢,我们来看两个大家都熟悉的生活场景。
10本不同的书放在书架,现重新摆放,使得每本书都不在原来的位置上,有几种摆法?

1个人给10个同学写信,但他把所有的信都装错了信封,问共有多少种错误的方式?

这些都是生活中的错排问题,推而广之,一个n个元素的排列,若一个排列中所有的元素都不在自己原来的位置上,那么这样的一个排列就称为原排列的一个错排。而研究一个排列的错排个数的问题,就称为错排问题。
错排问题,也叫做伯努利-欧拉错装信封问题,它是数学史上著名的数论问题。最早研究这个问题的是丹尼尔·伯努利。后来欧拉对此产生了兴趣,并独立解决了这个难题,并称其为“组合理论的一个妙题”。因此,历史上也将错排问题叫做“伯努利-欧拉装错信封问题”。
很明显,错位问题涉及到排列组合知识,首先能想到的自然是枚举算法,我们使用函数f(n)来表示n个数的错排总数。
当n = 1时,只有一个数字,不可能出现错排情况,所以f(1) = 0;
当n = 2时,全排列只有两种,分别是12和21,其中后者是错排,所以f(2) = 1;
当n = 3时,全排列有6种,分别是123、132、213、231、312、321,其中231和312是错排,所以f(3) = 2;
当n = 4时,全排列有24种,其中错排有9种,分别是2143、2341、 2413、3142、 3412、3421、 4123、4312、 4321,所以f(4) = 9;
......
枚举算法的编程实现是需要使用循环的,并且还是嵌套循环,嵌套的层数取决于n,n = 3时,使用3层循环,n = 4时,则为4层循环,以此类推。
随着n的增大,循环的次数越来越多,由于n是变化的, 直接使用枚举算法是无法编写代码的。
我们不妨换一个思路,对于n个元素的错排问题,可以将转化为 n - 1个元素的错排问题,它们只是规模大小不同,排列的算法其实是一样的。
因此,我们可以使用递推的思想来推导f(n)和f(n-1)之间的关系。
假定n - 1个元素是错排的,在增加第n个元素时,它是不能放在第n个位置(n的正确位置),那么它放在哪儿呢?
我们可以分两步来进行推导。
第一步,选择n的位置。
前面n - 1个元素任何一个位置都是可以的,假设放在第m位上(1 <= m <= n -1)。很显然,n的可选位置有n - 1种方案。
第二步,选择m的位置。
由于m被挤出来了, 需要考虑m的放置问题,m可以放哪些地方呢,此时又可以分两种情况:
-
放在n的位置,此时m和n的位置是固定的,错排就转化为除了m和n之外,其它n -2位的错排问题,即f(n - 2);
-
不放在n的位置,此时m的位置是固定的,错排就转化为除了m之外,其它n - 1位的错排问题,即f(n - 1);
因此,我们可以得出如下公式:

熟悉斐波那契数列的同学,应该对这个推导公式比较熟悉。
实际上,伟大的数学家欧拉早在200多年前就已经给出了这个递推公式,并解决了此题,然后将此题誉为“组合理论的一个妙题”。
有了递推公式,我们很容易就可以想到使用递归算法或者动态规划算法来编程实现。
接下来,我们进入具体的编程实现环节。
四.编程实现
根据上面的思路分析,我们使用两种方式来编写代码:
-
递归算法
-
动态规划
1.递归算法
根据前面的思路分析和递归算法的实现方式,需要先定义好递归函数,代码如下:

需要注意这里的两个if语句,这也是递归的出口,由于涉及到n - 1和n - 2,所以n = 1和n = 2时是不能直接使用推导公式的。
然后就可以调用递归函数计算出总的组合情况,代码如下:

递归的好处就是代码简洁,理解起来相对比较容易,缺点就是当递归层数较多时,执行时间太长,考试时有可能出现超时的情况。
2.动态规划
动态规划,英文Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。
对于动态规划,通常可以分成如下5个步骤:
-
确定dp数组以及下标的含义
-
确定递推公式
-
dp数组如何初始化
-
确定遍历顺序
-
举例推导dp数组
首先dp数组,在本题中,dp是一个一维列表,dp[i]表示i个盒子错排的方案数量。
递推公式在思路分析部分已经确定好了。
然后就是初始化了,我们只需要考虑dp[1]和dp[2]的情况即可。根据前面的分析,dp[1] = 0,dp[2] = 1。
我们先定义一个函数,用于计算错排数量,代码如下:

简单说明两点:
1). 为了方便计算,对于n个盒子,将列表长度设置为n + 1,其中dp[0]可以不用管,或者理解为n为0的情况;
2). 由于dp[1]和dp[2]是不能使用推导公式,所以循环需要在从n = 3开始,直到第n个元素结束,包括第n个元素。
接下来,获取用户输入,调用函数即可,代码如下:

如果我们将dp数组打印出来,可以看到如下结果:

这是n = 20的情况,测试程序,可以发现,随着n的增大,仍然可以在很短的时间内输出结果,这就是动态规划算法的强大之处了。
五.总结与思考
本题难度较大,考查的知识点主要包括:
-
处理输入数据;
-
函数的定义及使用;
-
列表的运算及操作;
-
递归算法;
-
动态规划算法;
作为初中组复赛压轴题,本题还是非常有难度的,这里的排列组合已经涉及到高中数学知识了。
虽然我们并不需要使用数学方法来解决,但要想完美的解决这个问题,需要理解并掌握动态规划算法。
给你留一个小小的思考题,除了上面提到的递归算法和动态规划算法,实际上还有两种算法可以解决,一是使用itertools中的permutations函数,二是使用迭代算法,赶紧动手尝试一下吧。
类似的错排问题还有不少,超平老师再给你来两题吧。
教室里有10个座位(1 ~ 10),10位同学分别坐在一个不同的位置上(1 ~ 10),现要求打乱所有同学的位置,打乱规则如下:所有的同学都不能出现在原来的位置上,问有多少种打乱的方法?
家中阳台有10盆不同的花,为保持新鲜感,希望每天重新摆放,使得每盆花都不在第一天放的位置。那么最多可以保持多少天每天摆法都不同?
你还有什么巧妙的解决方案吗,欢迎和超平老师交流。
如果你觉得文章对你有帮助,别忘了点赞和转发,予人玫瑰,手有余香😄
更多教程,请移步至“超平的编程课”gzh。
相关文章:

使用动态规划实现错排问题-2023年全国青少年信息素养大赛Python复赛真题精选
[导读]:超平老师计划推出《全国青少年信息素养大赛Python编程真题解析》50讲,这是超平老师解读Python编程挑战赛真题系列的第15讲。 全国青少年信息素养大赛(原全国青少年电子信息智能创新大赛)是“世界机器人大会青少年机器人设…...

大规模向量检索库Faiss学习总结记录
因为最近要使用到faiss来做检索和查询,所以这里只好抽出点时间来学习下,本文主要是自己最近学习的记录,来源于网络资料查询总结,仅用作个人学习总结记录。 Faiss的全称是Facebook AI Similarity Search,是FaceBook的A…...
SpringCloudAlibaba之Sentinel(一)流控篇
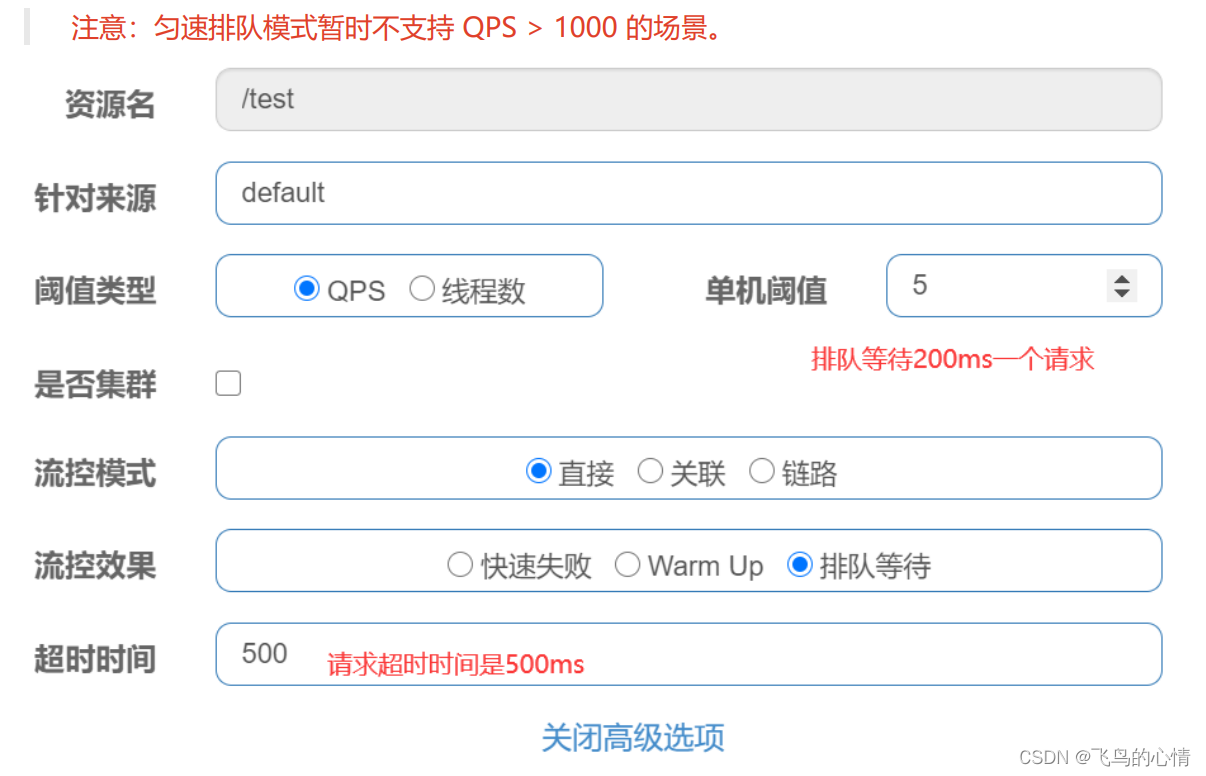
前言: 为什么使用Sentinel,这是一个高可用组件,为了使我们的微服务高可用而生 我们的服务会因为什么被打垮? 一,流量激增 缓存未预热,线程池被占满 ,无法响应 二,被其他服务拖…...

哪种模式ip更适合你的爬虫项目?
作为一名爬虫程序员,对于数据的采集和抓取有着浓厚的兴趣。当谈到爬虫ip时,你可能会听说过两种常见的爬虫ip类型:Socks5爬虫ip和HTTP爬虫ip。但到底哪一种在你的爬虫项目中更适合呢?本文将帮助你进行比较和选择。 首先,…...
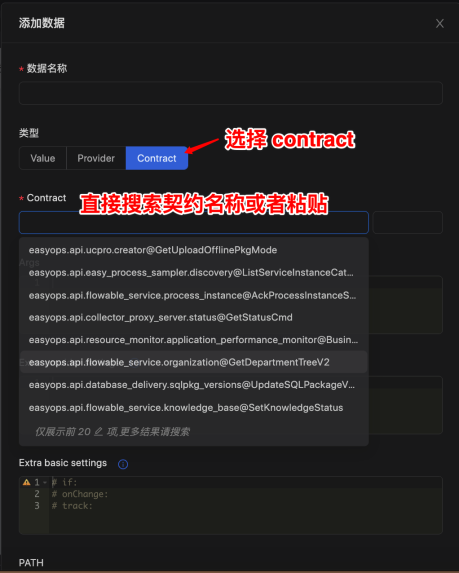
优维低代码实践:对接数据
优维低代码技术专栏,是一个全新的、技术为主的专栏,由优维技术委员会成员执笔,基于优维7年低代码技术研发及运维成果,主要介绍低代码相关的技术原理及架构逻辑,目的是给广大运维人提供一个技术交流与学习的平台。 优维…...

docker 离线模式-部署容器
有网络的情况下下载需要的镜像 比如(下面以tomcat为例子,其他镜像类似) docker pull tomcat打包镜像文件到本地 docker save tomcat -o tomcat.tar将tomcat.tar 上传到内网服务器(无外网环境) 导入镜像 docker load -i tomcat.tar创建容器…...

MDN-HTTP
参考资料 文章目录 HTTP简介HTTP 和 HTTPSHTTP消息典型的HTTP会话HTTP响应状态HTTP安全HTTP CookieHTTP压缩 HTTP简介 HTTP(Hypertext Transfer Protocol)是一种用于在计算机网络中传输超文本和其他资源的应用层协议。他是互联网的基础协议之一&#x…...

【数据库】PostgreSQL中使用`SELECT DISTINCT`和`SUBSTRING`函数实现去重查询
在PostgreSQL中,我们可以使用SELECT DISTINCT和SUBSTRING函数来实现对某个字段进行去重查询。本文将介绍如何使用这两个函数来实现对resource_version字段的去重查询。 1. SELECT DISTINCT语句 SELECT DISTINCT语句用于从表中选择不重复的记录。如果没有指定列名&…...
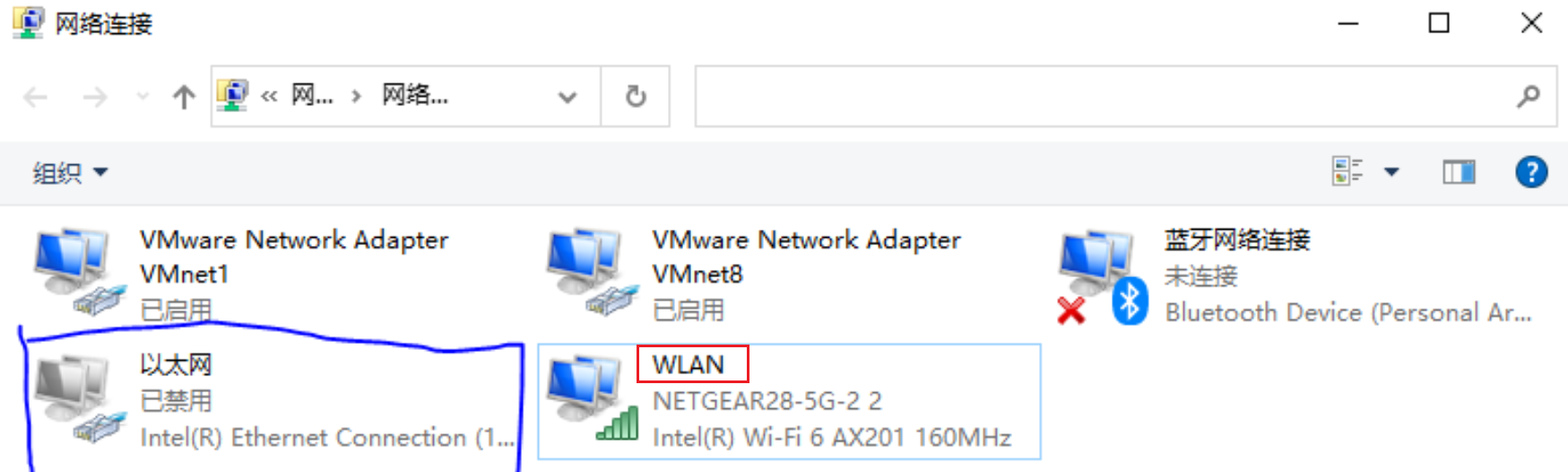
笔记本WIFI连接无网络【实测有效,不用重启电脑】
笔记本Wifi连接无网络实测有效解决方案 问题描述: 笔记本买来一段时间后,WIFI网络连接开机一段时间还正常连接,但是过一段时间显示网络连接不上,重启电脑太麻烦,选择编写重启网络脚本解决。三步解决问题。 解决方案&a…...
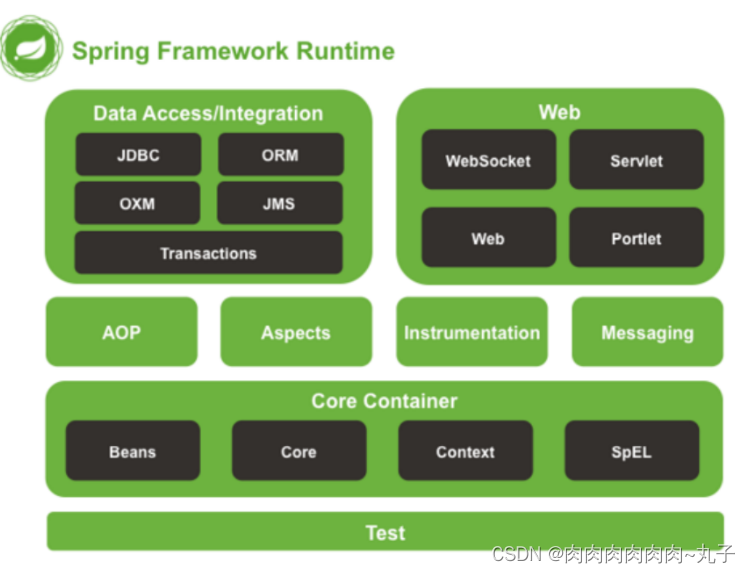
Java课题笔记~ Spring 概述
Spring 框架 一、Spring 概述 1、Spring 框架是什么 Spring 是于 2003 年兴起的一个轻量级的 Java 开发框架,它是为了解决企业应用开发的复杂性而创建的。Spring 的核心是控制反转(IoC)和面向切面编程(AOP)。 Spring…...
2022 robocom 世界机器人开发者大赛-本科组(国赛)
RC-u1 智能红绿灯 题目描述: RC-u1 智能红绿灯 为了最大化通行效率同时照顾老年人穿行马路,在某养老社区前,某科技公司设置了一个智能红绿灯。 这个红绿灯是这样设计的: 路的两旁设置了一个按钮,老年人希望通行马路时会…...

【雕爷学编程】Arduino动手做(195)---HT16k33 矩阵 8*8点阵屏模块6
37款传感器与模块的提法,在网络上广泛流传,其实Arduino能够兼容的传感器模块肯定是不止37种的。鉴于本人手头积累了一些传感器和执行器模块,依照实践出真知(一定要动手做)的理念,以学习和交流为目的&#x…...

Typescript]基础篇之 tsc 命令解析
[Typescript]基础[TOC]([Typescript]基础篇之 tsc 命令解析 tsc 命令概览编译参数说明--declaration--watch 这里是对 tsc 的一个详细介绍 tsc 命令概览 安装 Typescript 后可以使用 tsc 编译 ts 文件,tsc 命令是否支持其它参数 如果需要查看 tsc 支持的命令,或者…...
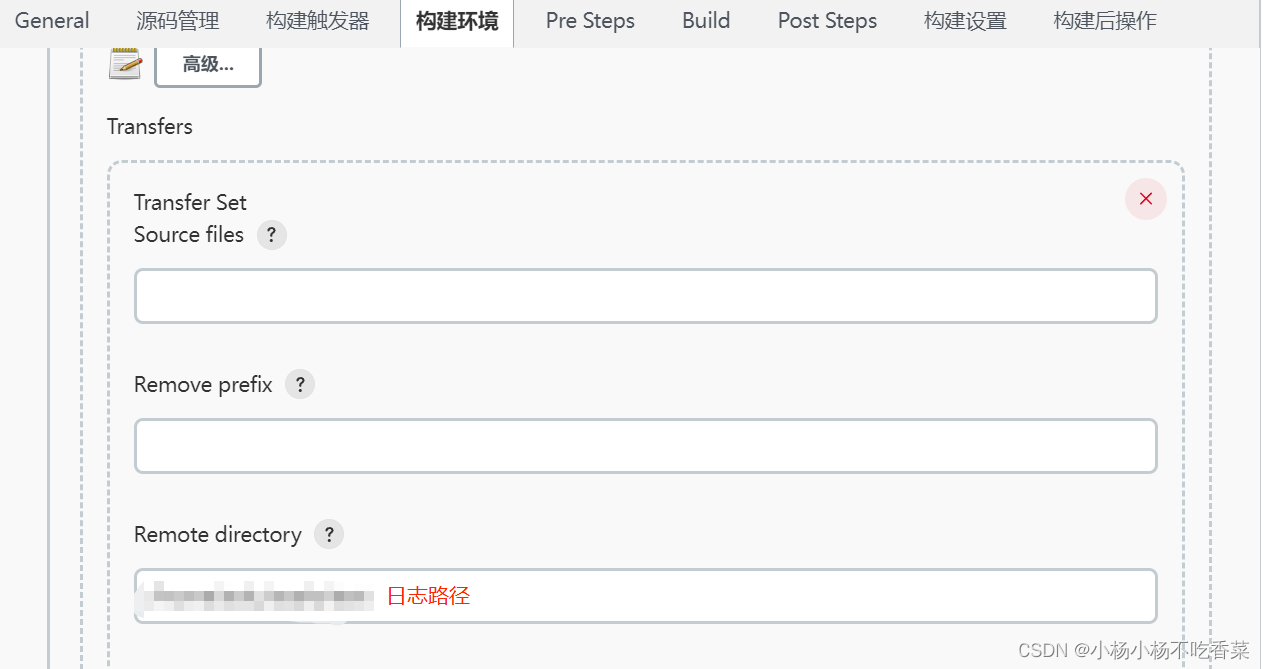
测试人员简单使用Jenkins
一、测试人员使用jenkins干什么? 部署测试环境 二、相关配置说明 一般由开发人员进行具体配置 1.Repository URL:填写git地址 2.填写开发分支,测试人员可通过相应分支进行测试环境的构建部署 当多个版本并行时,开发人员可以通过…...
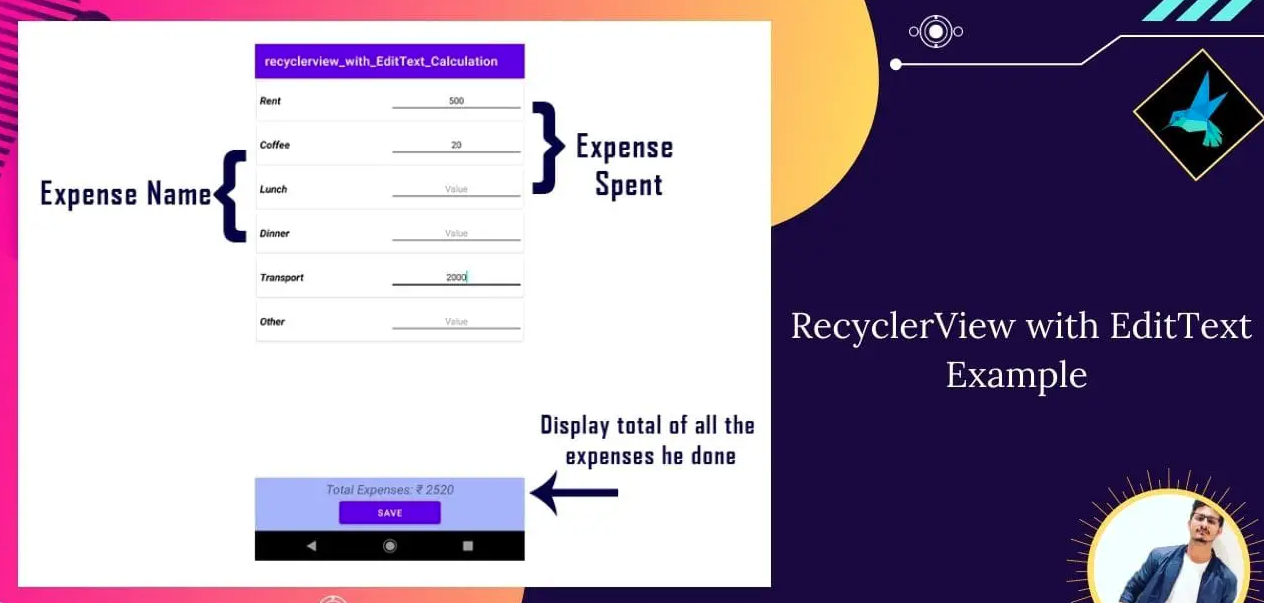
使用RecyclerView构建灵活的列表界面
使用RecyclerView构建灵活的列表界面 1. 引言 在现代移动应用中,列表界面是最常见的用户界面之一,它能够展示大量的数据,让用户可以浏览和操作。无论是社交媒体的动态流、商品展示、新闻列表还是任务清单,列表界面都扮演着不可或…...

linux ubuntu安装mysql
在 Ubuntu 上安装 MySQL 的步骤如下: 更新系统软件包列表: sudo apt update 安装 MySQL 服务器: sudo apt install mysql-server 安装完成,可以使用以下命令检查 MySQL 服务器是否正在运行: sudo systemctl status mysql 如果 MyS…...

计算机网络各层的功能以及常用协议
目录 1. 物理层(Physical Layer)2. 数据链路层(Data Link Layer)3. 网络层(Network Layer)4. 传输层(Transport Layer)5. 应用层(Application Layer) 计算机网…...
hdu7359)
M. Minimal and Maximal XOR Sum 2023“钉耙编程”中国大学生算法设计超级联赛(7)hdu7359
Problem - 7359 题目大意:给出一个n个数的排列,可以将任意区间内的所有数头尾翻转,每次操作的费用等于区间长度,要求将其变成一个递增排列,求消耗费用的异或和的最小值和最大值 1<n<1e5 思路:操作…...
内存模型及详细示例)
C++基础篇(五)内存模型及详细示例
目录 一、内存分区模型二、内存分区代码示例三、new 运算符详解 一、内存分区模型 C程序在运行时,将内存分为四个区域,不同的区域赋予不同的生命周期,以提供强大的灵活编程。 代码区:存储程序的二进制代码,通常是只读…...

基于 JMeter API 开发性能测试平台
目录 背景: 常用的 JMeter 类和功能的解释: JMeter 编写性能测试脚本的大致流程示意图: 源码实现方式: (1) 环境初始化 (2) 环境初始化 (3) 创建测试计划 (4) 创建 ThreadGroup (5) 创建循环控制器 (6) 创建 Sampler (…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...
)
2025.6.9总结(利与弊)
凡事都有两面性。在大厂上班也不例外。今天找开发定位问题,从一个接口人不断溯源到另一个 接口人。有时候,不知道是谁的责任填。将工作内容分的很细,每个人负责其中的一小块。我清楚的意识到,自己就是个可以随时替换的螺丝钉&…...

RabbitMQ 各类交换机
为什么要用交换机? 交换机用来路由消息。如果直发队列,这个消息就被处理消失了,那别的队列也需要这个消息怎么办?那就要用到交换机 交换机类型 1,fanout:广播 特点 广播所有消息:将消息…...
