【vue3】基础知识点-setup语法糖
学习vue3,都会从基础知识点学起。了解setup函数,ref,recative,watch、comptued、pinia等如何使用
今天说vue3组合式api,setup函数
在学习过程中一开始接触到的是这样的,定义数据且都要通过return返回
<script>
export default {
setup(){
cosnt message = 'new day
const logMessage= ()=>{
console.log(message)
}
return {
message,
logMessage
}
}
}
</script>
最新接触到的是这样的
<script setup>
cosnt message = 'new day
const logMessage= ()=>{
console.log(message)
}
</script>
两种不同的写法,那区别是什么呢?
其实在script标签上直接加setup就是语法糖写法
语法糖写法,简单理解就是经过一定的封装,将之前复杂的写法变成一个简单的写法
原先的export default 、setup(){} ,return 都不需要写了
官方提供了一个工具,可以在线看实际运行后的代码
戳这里,跳转到vue SFC Playground官方工具
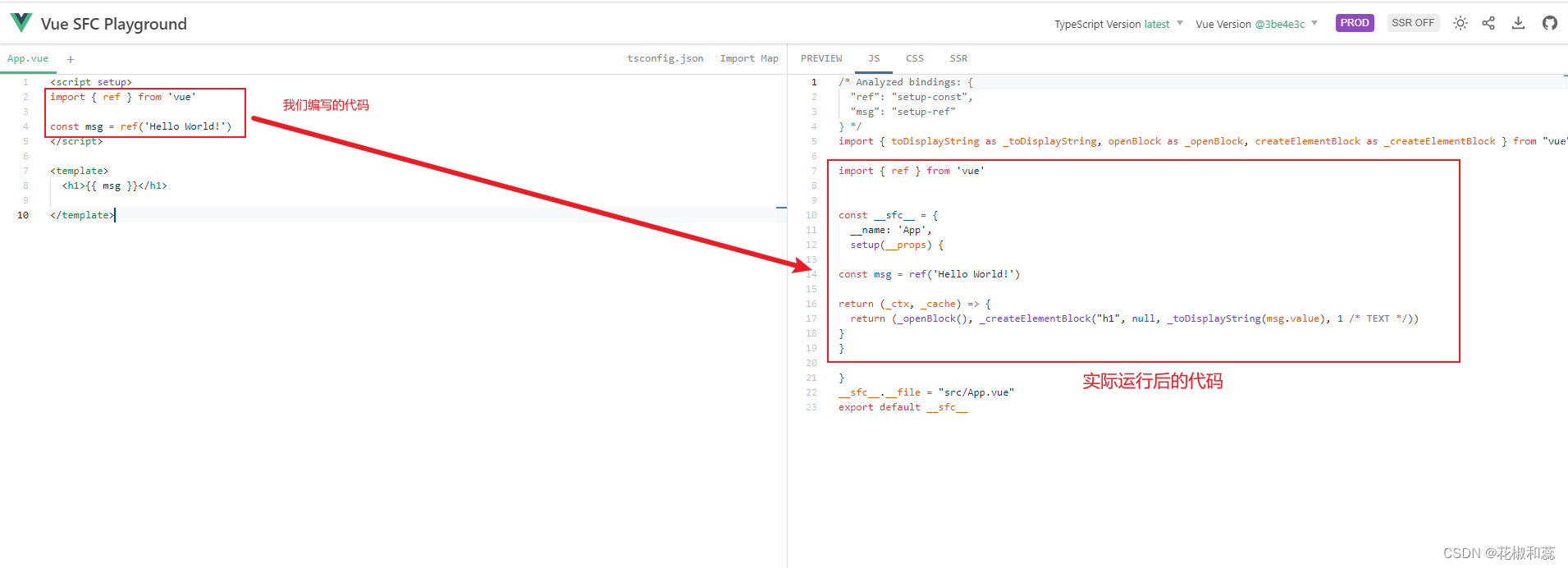
看右侧实际运行的代码,是同之前的复杂写法的。在底层运行的时候还是一开始的复杂写法,只是通过封装,提供给我们一个简单的写法,这就是语法糖的意义。
相关文章:

【vue3】基础知识点-setup语法糖
学习vue3,都会从基础知识点学起。了解setup函数,ref,recative,watch、comptued、pinia等如何使用 今天说vue3组合式api,setup函数 在学习过程中一开始接触到的是这样的,定义数据且都要通过return返回 <…...

idol!! 2023牛客暑期多校训练营6 C
登录—专业IT笔试面试备考平台_牛客网 题目大意:定义n!!等于与n的奇偶性相同的所有小于等于n的数的阶乘之和,问n!!的末尾有多少0 1<n<1e18 思路:因为末尾0的来源是2*5,而2的个数明显比5的个数多得多,所以末尾…...
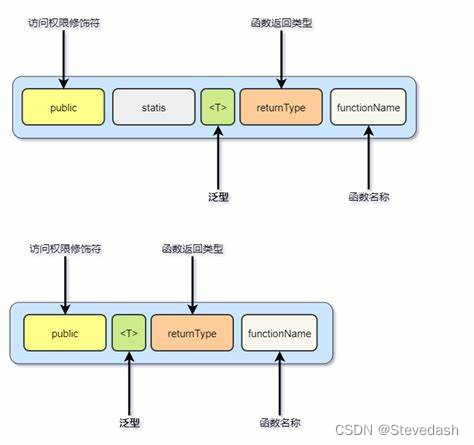
深入理解Jdk5引入的Java泛型:类型安全与灵活性并存
深入理解Jdk5引入的Java泛型:类型安全与灵活性并存 在Java的中,有一个强大的工具,它可以让你在编写代码时既保持类型安全,又享受灵活性。**这个工具就是——泛型(Generics)。**本文将引导你深入了解Java…...
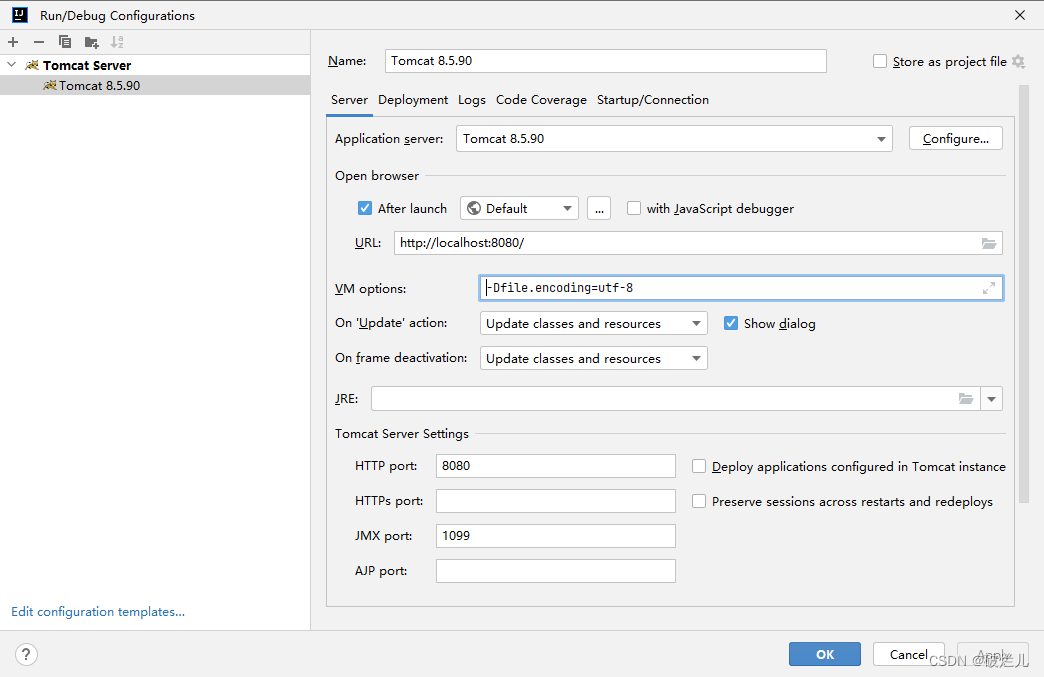
idea在控制台中输出文字显示乱码
VM options中加入下面这行 -Dfile.encodingutf-8...
hacksudo3 通关详解
环境配置 一开始桥接错网卡了 搞了半天 改回来就行了 信息收集 漏洞发现 扫个目录 大概看了一眼没什么有用的信息 然后对着login.php跑了一下弱口令 sqlmap 都没跑出来 那么利用点应该不在这 考虑到之前有过dirsearch字典太小扫不到东西的经历 换个gobuster扫一下 先看看g…...
)
CentOS 虚拟机磁盘扩容(非常实用)
新手村的选手在刚开始安装使用 CentOS 虚拟机时,很多选项都会按照推荐操作来,比如:磁盘推荐大小为 20 GB;但随着后面的使用,总会因为“磁盘根目录不足”原因,而导致软件无法安装、虚拟机无法正常运行等&…...
docker案例复现
$uri导致的CRLF注入漏洞 前期准备dockerdocker compose 漏洞配置 前期准备 docker 要完成这样的测试,需要我们有一定的环境,也就是需要大家去安装docker 更新系统软件包: sudo yum update 安装 Docker 的依赖软件包: sudo yum …...

淘宝资源采集(从零开始学习淘宝数据爬取)
1. 为什么要进行淘宝数据爬取? 淘宝数据爬取是指通过自动化程序从淘宝网站上获取数据的过程。这些数据可以包括商品信息、销售数据、评论等等。淘宝数据爬取可以帮助您了解市场趋势、优化您的产品选择以及提高销售额。 淘宝作为全球的电商平台,每天都有…...
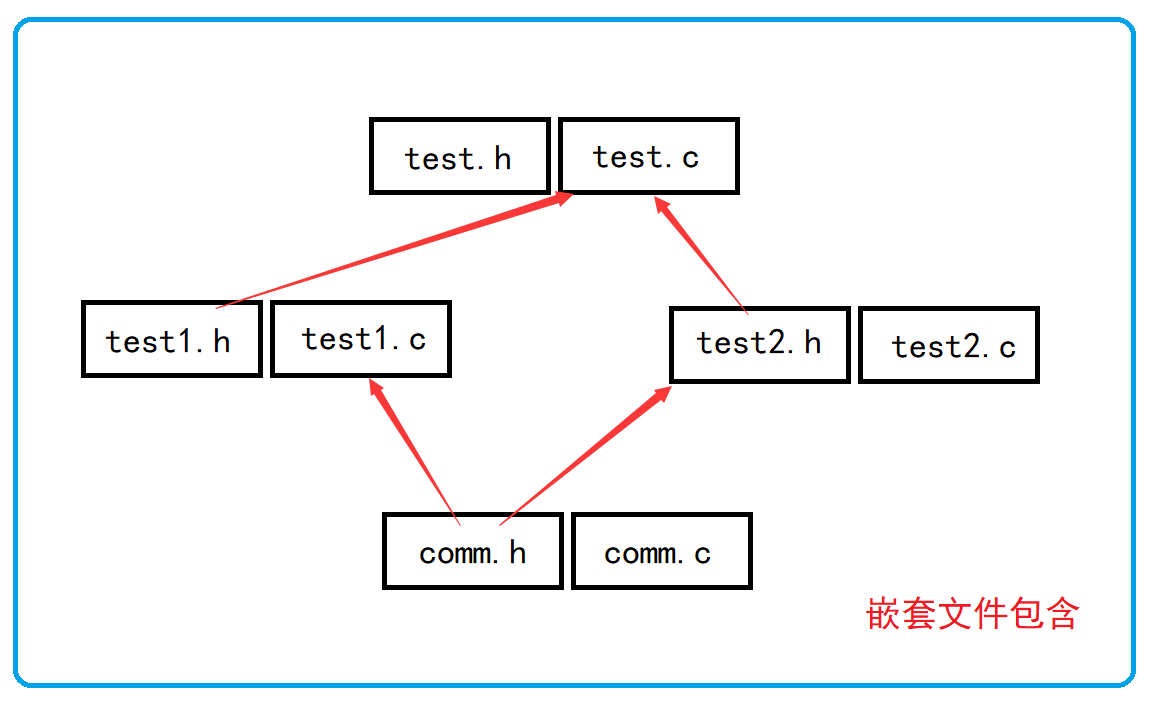
【C语言】预处理详解
本文目录 1 预定义符号 2 #define 2.1 #define 定义标识符 2.2 #define 定义宏 2.3 #define 替换规则 2.4 #和## 2.5 带副作用的宏参数 2.6 宏和函数对比 2.7 命名约定 3 #undef 4 命令行定义 5 条件编译 6 文件包含 6.1 头文件被包含的方式 6.2 嵌套文件包含 1 预定义符号 __…...

2023中国(合肥)场景创新峰会成功举办,全息网御被纳入《合肥市第二批场景能力清单》
场景作为重要的城市资源,在驱动科技创新、产业发展、城市治理方面发挥着重要作用。近年来,为促进数字技术与实体经济深度融合,加速前沿科技转化落地、吸引全球创新资源集聚,合肥市聚焦“双找”:为产品找场景࿰…...
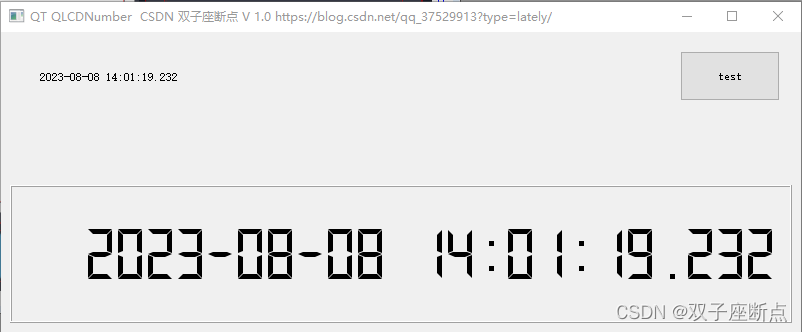
QT QLCDNumber 使用详解
本文详细的介绍了QLCDNumber控件的各种操作,例如:新建界面、源文件、设置显示位数、设置进制、设置外观、设置小数点、设置溢出、显示事件、其它文章等等操作。 实际开发中,一个界面上可能包含十几个控件,手动调整它们的位置既费时…...
明年,HarmonyOS不再兼容Android应用!
2023年华为开发者大会,不知道各位老铁们是否观看了,一个震撼的消息就是,首次公开了HarmonyOS NEXT的概念,简而言之就是,这是一款专为开发者打造的预览版操作系统,旨在提供"纯正鸿蒙操作系统"的体…...
)
华为OD机试 - 人气最高的店铺(Java JS Python)
题目描述 某购物城有m个商铺,现决定举办一场活动选出人气最高店铺。 活动共有n位市民参与,每位市民只能投一票,但1号店铺如果给该市民发放 q 元的购物补贴,该市民会改为投1号店铺。 请计算1号店铺需要最少发放多少元购物补贴才能成为人气最高店铺(即获得的票数要大于其…...

mysql sql 语句sum求和嵌套数学表达式
今天有个需求, 已减高度 高度 x 单双开(单开1 双开2) x 2,要直接写在sql语句中。 表字段 包含 高度 和 单双开字段 值是字符串 (双开 左单开 右单开) -- 已减高度 2 * 单双开 * 高度 sum( -- 求和 表达式 已减高度 2 * 单双开 * 高度 t_cloth.hegiht * 2 * (case WHEN l…...
Java课题笔记~ Servlet编程
1.Servlet编程基础 (1)什么是Servlet Servlet是基于Java语言的Web编程技术,部署在服务器端的Web容器里,获取客户端的访问请求,并根据请求生成响应信息返回给客户端。 创建Servlet的方式,有 如下图:一般创建Servlet都…...

修改IDEA的idea.vmoptions参数导致IDEA无法打开(ReservedCodeCacheSize)
事发原因 Maven导依赖的时候OOM,因此怀疑是内存太小,尝试修改idea.vmoptions的参数,然后发现IDEA重启后打不开了,卸载重装后也无法打开。。。 实际上如果导包爆出OOM的话应该调整下图参数,不过这都是后话了 解决思路…...

P1321 单词覆盖还原
题目描述 一个长度为 l l l 的字符串中被反复贴有 boy 和 girl 两单词,后贴上的可能覆盖已贴上的单词(没有被覆盖的用句点表示),最终每个单词至少有一个字符没有被覆盖。问贴有几个 boy 几个 girl? 输入格式 一行被…...
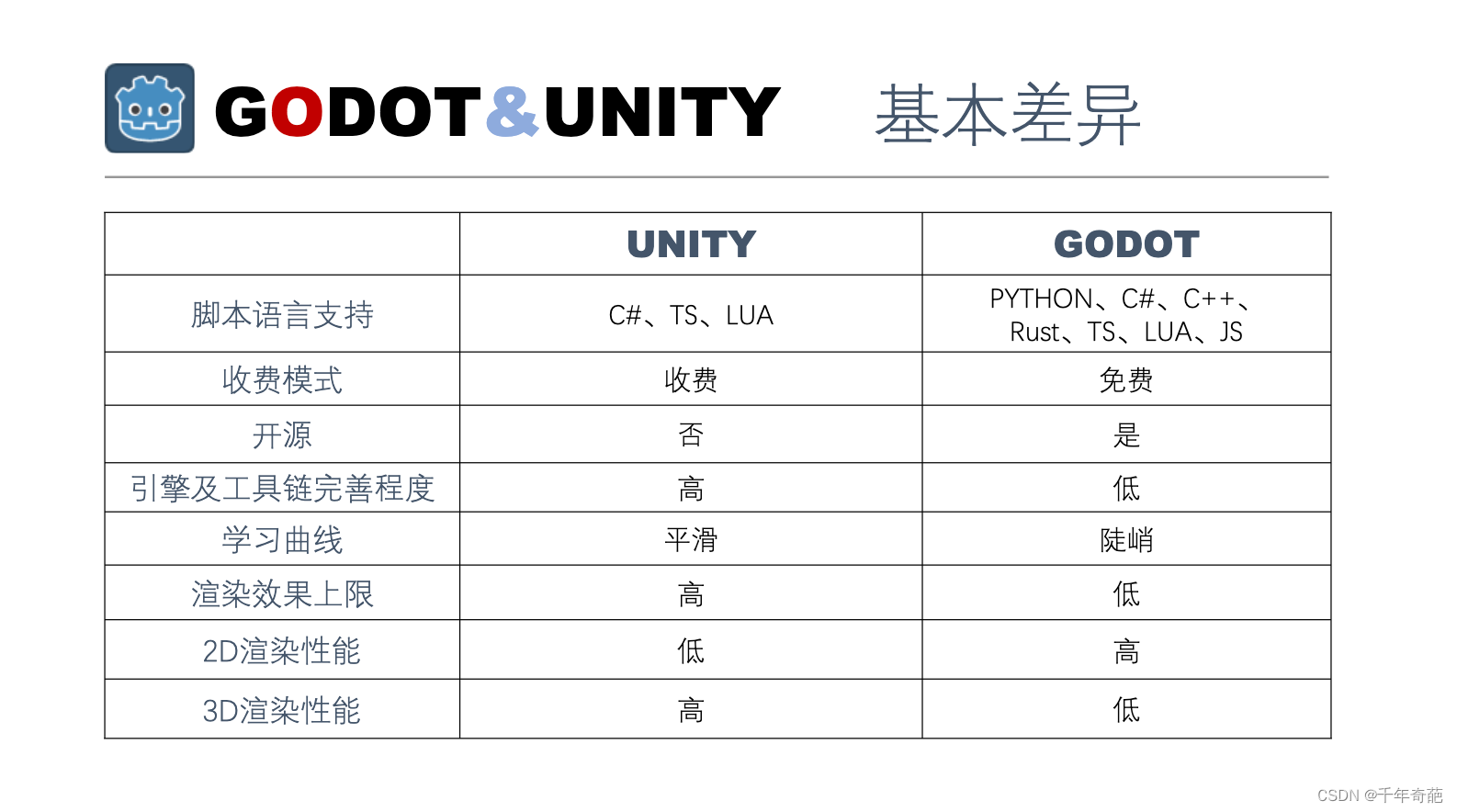
GODOT游戏引擎简介,包含与unity性能对比测试,以及选型建议
GODOT,是一个免费开源的3D引擎。本文以unity作对比,简述两者区别和选型建议。由于是很久以前写的ppt,技术原因视频和部分章节丢失了。建议当做业务参考。 GODOT目前为止遇到3个比较重大的基于,第一个是oprea的合作奖,…...
Add-in Express for Microsoft Office and Delphi Crack
Add-in Express for Microsoft Office and Delphi Crack 适用于Microsoft Office和Delphi VCL的Add-in Express使您能够在几次点击中为Microsoft Office开发专业插件。它生成基于COM的项目,这些项目包含Microsoft Office外接程序或智能标记的所有必要功能࿰…...

opencv基础-34 图像平滑处理-2D 卷积 cv2.filter2D()
2D卷积是一种图像处理和计算机视觉中常用的操作,用于在图像上应用滤波器或卷积核,从而对图像进行特征提取、平滑处理或边缘检测等操作。 在2D卷积中,图像和卷积核都是二维的矩阵或数组。卷积操作将卷积核在图像上滑动,对每个局部区…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

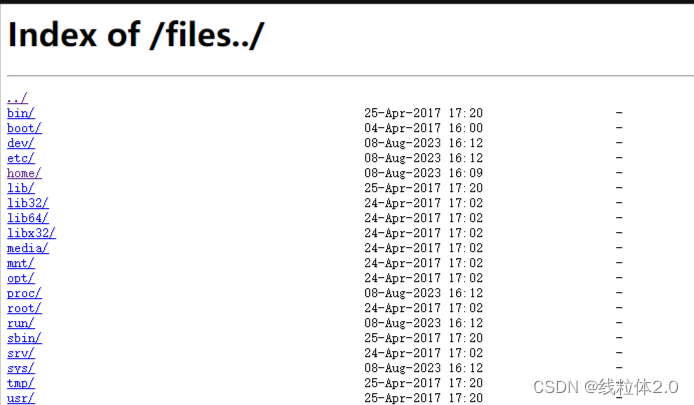
Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...
——统计抽样学习笔记(考试用))
统计学(第8版)——统计抽样学习笔记(考试用)
一、统计抽样的核心内容与问题 研究内容 从总体中科学抽取样本的方法利用样本数据推断总体特征(均值、比率、总量)控制抽样误差与非抽样误差 解决的核心问题 在成本约束下,用少量样本准确推断总体特征量化估计结果的可靠性(置…...
