编程中的宝藏:二分查找
二分查找
假设你需要在电话簿中找到一个以字母 “K” 开头的名字(虽然现在谁还在用电话簿呢!)。你可以从头开始翻页,直到进入以 “K” 打头的部分。然而,更明智的方法是从中间开始,因为你知道以 “K” 打头的名字很可能在电话簿的中间部分。
类似地,当你要在字典中查找一个以字母 “O” 开头的单词时,你也会从中间附近开始搜索。
再举一个例子,当你登录 Facebook 时,系统需要核实你是否有该网站的账户。它必须在数据库中查找你的用户名。如果你的用户名是 “karlmageddon”,Facebook 可以从以字母 “A” 开头的部分开始查找。然而,更聪明的做法是从中间开始查找。
这些场景都涉及到查找问题,而在所有这些情况下,都可以使用同一种算法来解决,那就是二分查找。
二分查找是一种算法,它的输入是一个有序元素列表(必须有序的原因稍后解释)。如果要查找的元素包含在列表中,二分查找会返回其位置;否则返回 -1。
下面的示例演示了二分查找的工作原理。我们随意选择一个在 1 到 100 之间的数字。

你的目标是以最少的猜测次数猜到这个数字。每次猜测后,我会告诉你是小了、大了还是猜对了。如果你从 1 开始顺序猜测,过程可能是这样的:
- 猜测 1 -> 小了
- 猜测 2 -> 小了
- 猜测 3 -> 小了
- …
这种方法被称为简单查找,更确切地说是傻找。每次猜测只能排除一个数字。如果数字是 99,你最多需要猜测 99 次才能猜对。
更聪明的查找方法
下面是一种更聪明的猜测方法:从 50 开始。
- 猜测 50 -> 小了,但排除了一半的数字!现在你知道 1 到 50 都是小了。接下来,你猜 75。
- 猜测 75 -> 大了,又排除了一半的数字!使用二分查找,你猜测的是中间的数字,从而每次都可以排除一半的数字。然后,你猜测 63(50 和 75 之间的数字)。
这就是二分查找,你刚刚学会了一种全新的算法!每次猜测都会排除一半的数字,如下图所示:

不论我心里想的是哪个数字,你最多需要 7 次猜测就能找到,因为每次猜测都会排除很多数字。对比一下:
- 简单查找:100 步
- 二分查找:7 步
也许在使用者的角度看,这 97 步的差距似乎微不足道。然而,随着元素数量的增加,二分查找的优势会越来越明显。
现在,让我们考虑一个问题:如果你要在包含 240,000 个单词的字典中查找一个单词,最多需要多少步?假设要查找的单词位于字典的末尾,使用简单查找将需要 240,000 步。而如果使用二分查找,每次都会排除一半的单词,直到最后只剩下一个单词。
在进行二分查找时,每次排除的单词数量是通过将搜索范围减半来计算的。因为字典中有 240,000 个单词,每次排除一半,我们可以计算出每次排除的单词数量,如下:
- 初始范围:240,000 个单词
- 第 1 次排除:120,000 个单词
- 第 2 次排除:60,000 个单词
- …(后续步骤省略)
因此,使用二分查找,最多需要 18 次排除就能找到一个特定单词,即使在包含 240,000 个单词的字典中。这是因为每一次排除一半的单词,使得搜索范围迅速减小,直到只剩下一个单词。
仅当列表是有序的时候,二分查找才适用。例如,电话簿中的名字按字母顺序排列,因此可以使用二分查找来查找名字。
运行时间
让我们再次回到二分查找。使用二分查找相比于简单查找能节省多少时间呢?简单查找是逐个地检查数字,如果列表包含 100 个数字,最多需要猜测 100 次。而如果列表包含 40 亿个数字,最多需要猜测 40 亿次。换句话说,最多需要的猜测次数与列表的长度相同,这种情况被称为线性时间(linear time)。
然而,二分查找则不同。如果列表包含 100 个元素,最多只需猜测 7 次;如果列表包含 40 亿个数字,最多只需猜测 32 次。相比之下,二分查找的运行时间是对数时间(logarithmic time)。
下表总结了我们所发现的情况:
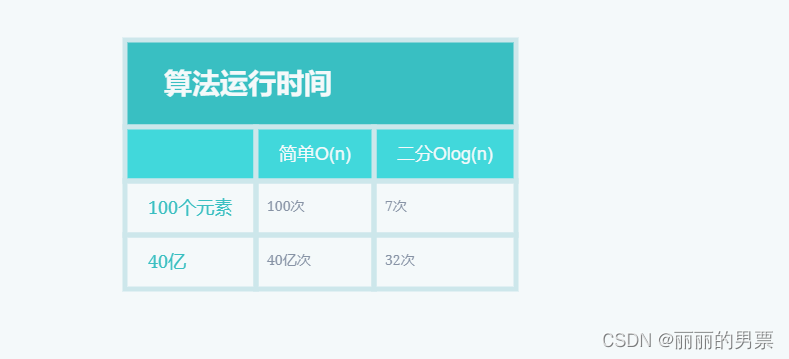
总结
当我们进一步探讨二分查找和简单查找之间的差异时,不难发现,二分查找的性能优势随着元素数量的增加变得更加显著。虽然在开始时,二分查找的速度提升可能并不明显,但随着列表规模的增长,它的优越性将愈发凸显出来。
简单查找以线性时间的方式进行,每增加一个元素,它需要的额外时间也会线性增长。这就导致当元素数量庞大时,每次查找都会变得耗时且不实际。例如,如果你有一个拥有数百万个元素的数据集,使用简单查找进行查询可能会变得极其缓慢,甚至不切实际。然而,二分查找以对数时间的方式运作,每次查找只需要排除一半的元素。
这意味着,尽管数据量增加,每次查找所需的额外时间增长得非常缓慢。就像是在探索一个迷宫时,你只需每次选择一个正确的路径,逐渐逼近目标,而不是逐一检查所有可能的路径。
这种对数级别的优越性意味着,在大数据集或者长列表中,二分查找的速度几乎不会受到影响。它的查询速度可以在常数时间内保持,无论数据规模如何增长。而这也是为什么在现代计算机科学中,二分查找是一种备受推崇的高效算法。
因此,无论是在简单的名字查找、大规模数据处理,还是搜索庞大的字典中的单词,二分查找都是一种强大的工具,能够在海量信息中快速找到目标。在信息爆炸的今天,掌握并充分利用这种高效的算法,对于优化搜索效率、提升数据处理速度至关重要。
代码示例
Python
def binary_search(lst, item):left = 0right = len(lst) - 1while left <= right:# 你每次都检查中间的元素。mid = (left + right) // 2val = lst[mid]if val == item:return midif val > item:# 如果猜的数字大了,就修改rightright = mid - 1else:# 如果猜的数字小了,就相应地修改left。left = mid + 1return -1 # Return -1 if item is not foundmy_list = [1, 2, 3, 4, 5, 6, 7, 8]print(binary_search(my_list, 6))
Java
public class BinarySearch {public static int binarySearch(int[] arr, int target) {int left = 0;int right = arr.length - 1;while (left <= right) {int mid = (left + right) / 2;int val = arr[mid];if (val == target) {return mid;}if (val > target) {right = mid - 1;} else {left = mid + 1;}}return -1;}public static void main(String[] args) {int[] myArray = {1, 2, 3, 4, 5, 6, 7, 8};int searchItem = 6;int result = binarySearch(myArray, searchItem);System.out.println(result);}
}相关文章:

编程中的宝藏:二分查找
二分查找 假设你需要在电话簿中找到一个以字母 “K” 开头的名字(虽然现在谁还在用电话簿呢!)。你可以从头开始翻页,直到进入以 “K” 打头的部分。然而,更明智的方法是从中间开始,因为你知道以 “K” 打头…...
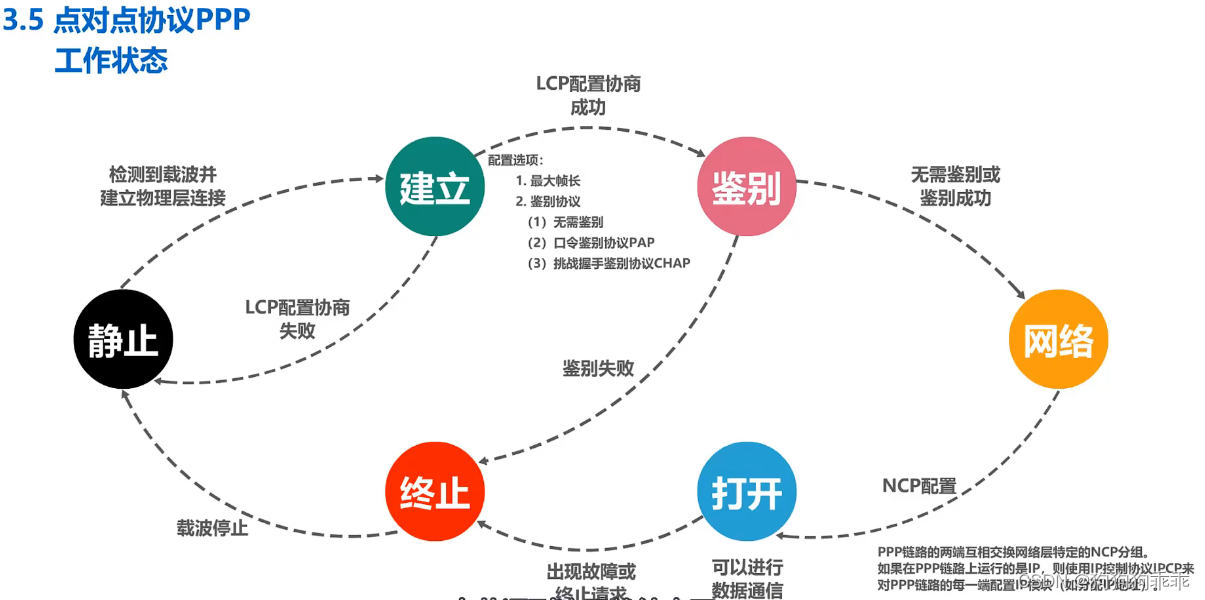
计算机网络 数据链路层
...

如何维护自己的电脑
目录 1、关于电脑选择的建议 1.1、价格预算 1.2、明确需求 1.3、电脑配置 1.4、分辨率 1.5、续航能力 1.6、品牌选择 1.7、用户评测 1.8、各个电商平台对比 1.9、最后决策 2、我的选择 3、电脑保养 3.1 外部清洁 3.2 安装软件 3.3 优化操作系统 3.4 维护硬件设…...

智能优化算法——哈里鹰算法(Matlab实现)
目录 1 算法简介 2 算法数学模型 2.1.全局探索阶段 2.2 过渡阶段 2.3.局部开采阶段 3 求解步骤与程序框图 3.1 步骤 3.2 程序框图 4 matlab代码及结果 4.1 代码 4.2 结果 1 算法简介 哈里斯鹰算法(Harris Hawks Optimization,HHO),是由Ali As…...
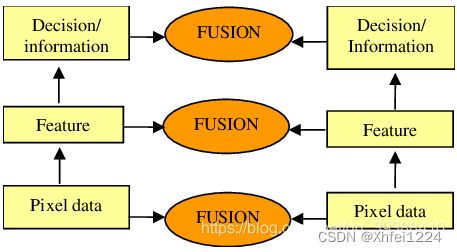
【深度学习】多粒度、多尺度、多源融合和多模态融合的区别
多粒度(multiresolution)和多尺度(multiscale) 多粒度(multiresolution)和多尺度(multiscale)都是指在不同的空间或时间尺度上对数据或信号进行分析和处理。其中 多尺度࿱…...

利用SCCM进行横向移动
01SCCM介绍 SCCM全名为System Center Configuration Manager,从版本1910开始,微软官方将其从Microsoft System Center产品移除,重新命名为Microsoft Endpoint Configuration Manager(ConfigMgr),其可帮助 …...
Nginx 负载均衡
Nginx 负载均衡 负载均衡由反向代理来实现的 其中反向代理分为七层代理和四层代理,一般常用的是七层代理,接下来分别介绍一些 NGINX 七层代理 七层是最常用的反向代理方式,只能配置在Nginx配置文件的http模块。 配置方法名称:…...
Java课题笔记~ ServletConfig
概念:代表整个web应用,可以和程序的容器(服务器)来通信 <?xml version"1.0" encoding"UTF-8"?> <web-app xmlns"http://java.sun.com/xml/ns/javaee"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instan…...

oracle的异常处理
oracle提供了预定义例外、非预定义例外和自定义例外三种类型。其中: l预定义例外用于处理常见的oracle错误; l非预定义例外用于处理预定义所不能处理的oracle错误; l自定义例外处理与oracle错误无关的其他情况。 Oracle代码编写过程中&am…...
【MySQL】MySQL数据类型
文章目录 一、数据类型的分类二、tinyint类型2.1 创建有符号数值2.2 创建无符号数值 三、bit类型三、浮点类型3.1 float3.2 decimal类型 四、字符串类型4.1 char类型4.2 varchar类型 五、日期和时间类型六、枚举和集合类型6.1 enum的枚举值和set的位图结构6.2 查询集合find_in_…...
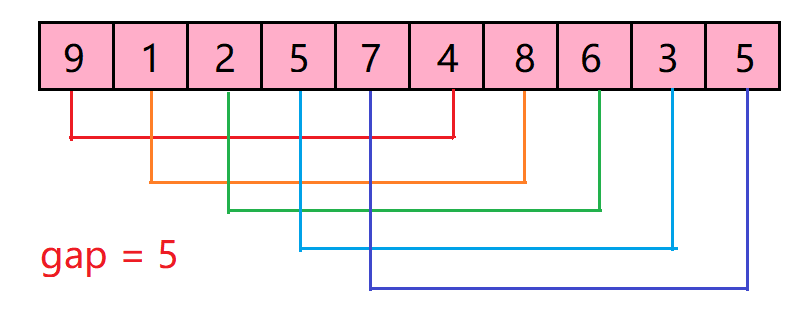
【数据结构与算法】十大经典排序算法-希尔排序
🌟个人博客:www.hellocode.top 🏰Java知识导航:Java-Navigate 🔥CSDN:HelloCode. 🌞知乎:HelloCode 🌴掘金:HelloCode ⚡如有问题,欢迎指正&#…...

docker 常用命令
1. 搜索并下载镜像 docker search bundlefusion # 搜索docker pull jhljx/bundlefusion # 将远程仓库文件下载到本地2. 用镜像创建容器 docker run -it --namebundlefusion colec777/bundlefusion-cu11.4-cudagl:v8 /bin/bash # 创建并运行 exit # 退出终端 sudo docker cont…...
uniapp微信小程序中打开腾讯地图获取用户位置信息
实现的效果 第一步:首先登录微信公众平台 , 需要用到AppID 第二步: 注册登录腾讯位置服务 注册需要手机号和邮箱确认,然后创建应用 创建后点击添加key 添加后会生成key,后面会用到这个key 第三步: 登录微信公众平台&a…...
嵌入式领域:人才供需失衡,发展潜力巨大
嵌入式技术正快速发展,ARM处理器、嵌入式操作系统、LINUX等技术助力嵌入式领域崛起。然而,行业新颖且门槛高,缺乏专业指导。因此,嵌入式人才稀缺,身价水涨船高。 未来几年,嵌入式系统将在信息化、智能化、…...

python 书籍
python高手进阶之路 10册 QQ:417398600...

Debian纯净系统安装php常用扩展和程序
适用于 php-fpm debian容器 mysql扩展 docker-php-ext-install pdo_mysql docker-php-ext-install mysqliredis扩展 pecl install redis docker-php-ext-enable redis# pecl无法装就: docker-php-source extract # 创建并初始化 /usr/src/php目录(扩展…...
vue+element中如何设置单个el-date-picker开始时间和结束时间关联
功能:选了开始时间,则结束时间只能选择开始时间之后的;选了结束时间,则开始时间只能选择结束时间之前的 重点是picker-options属性 图示: 代码展示: // body 内部<el-form-item><el-date-pickerv-model&qu…...

二次封装ajax和axios
ajax app.config.globalProperties.$http function(url, method, data, async, fun) {$.ajax({url: baseUrl url, //请求地址type: method, //请求方式dataType: json, //数据类型contentType: "application/json",xhrFields: { //跨域设置withCredentials: t…...
Android进阶之SeekBar动态显示进度
SeekBar 在开发中并不陌生,默认的SeekBar是不显示进度的,当然用吐司或者文案在旁边实时显示也是可以的,那能不能移动的时候才显示,默认不显示呢,当然网上花哨的三方工具类太多了,但是我只是单纯的想在SeekBar的基础上去添加一个可以跟随移动显示的气泡而…...

企业计算机服务器中了locked勒索病毒怎么办,如何预防勒索病毒攻击
计算机服务器是企业的关键信息基础设备,随着计算机技术的不断发展,企业的计算机服务器也成为了众多勒索者的攻击目标,勒索病毒成为当下计算机服务器的主要攻击目标。近期,我们收到很多企业的求助,企业的服务器被locked…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
