【对于一维信号的匹配】对一个一维(时间)信号y使用自定义基B执行匹配追踪(MP)研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
对一个一维(时间)信号y使用自定义基B执行匹配追踪(MP)。
匹配追踪(Mallat和Zhang 1993)是一种贪婪算法,用于通过字典元素D(y〜Dw)的加权和(w)来获取信号y的稀疏表示。稀疏表示意味着大多数元素等于0(nnz(w) << length(y))。这种稀疏表示在许多不同的情况下都很有用:用于获取时频谱图,降噪信号,压缩信号等等。
对于时间信号,自然地使用字典元素D,由位于每个可能的时间点上的基本元素B组成。在这种情况下,权重形成一个高度过完备的字典中的卷积或平移不变的稀疏编码形式。
对于一维信号的匹配追踪(Matching Pursuit, MP)是一种研究方法,用于对一维(时间)信号进行分析和表示。该方法使用自定义基B来执行匹配追踪算法,以获得信号y的稀疏表示。
匹配追踪是一种贪婪算法,旨在通过将信号表示为字典元素的加权和来获得其稀疏表示。稀疏表示意味着信号的大部分元素都是零,只有少数非零元素。这种表示方法在许多领域都有广泛的应用,例如时频谱图的生成、信号降噪和信号压缩等。
对于一维信号,选择合适的基B是非常重要的。基B通常由基本元素组成,这些元素在不同的时间点上进行平移。通过使用这样的基础元素,可以构建一个高度过完备的字典,从而实现对信号的卷积或平移不变的稀疏编码。
通过对一维信号进行匹配追踪研究,我们可以更好地理解信号的特征和结构,从而为信号处理和分析提供更多的工具和方法。
📚2 运行结果

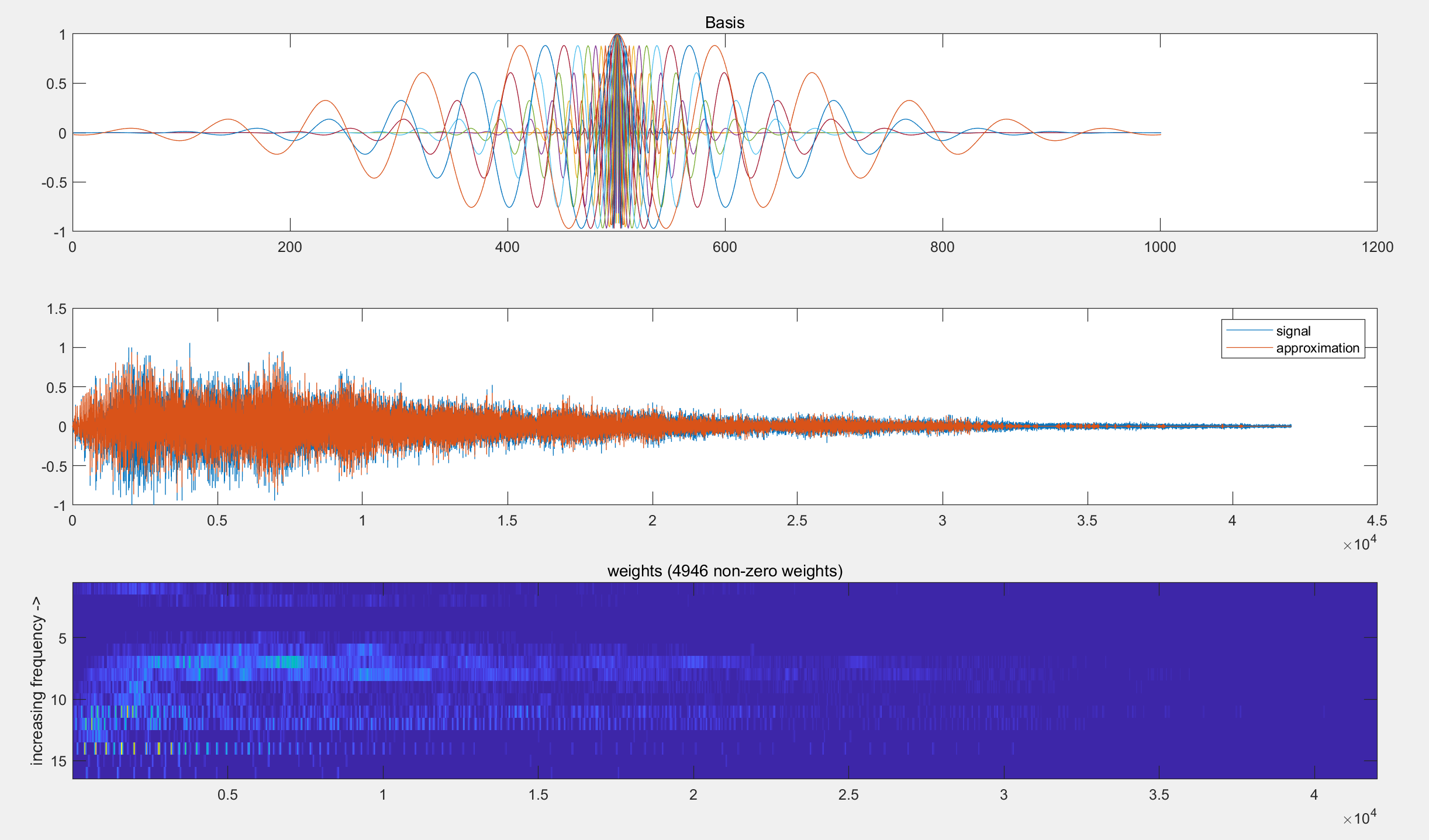 部分代码:
部分代码:
%% Same, but this time only allow positive weights
%Express gong signal as a sparse sum of Gabors
[ws2,r2] = temporalMP(sig.y,gabors,true,5000);
%%
subplot(3,1,1);
plot(gabors);
title('Basis');
subplot(3,1,2);
plot([sig.y,r2]);
legend('signal','approximation');
subplot(3,1,3);
%the convolution here is to make the spikes visible
imagesc(conv2(ws2,exp(-rg.^2/2/20^2),'same')');
ylabel('increasing time ->');
ylabel('increasing frequency ->');
title(sprintf('weights (%d non-zero weights)',nnz(ws(:))));
%%
%listen to the original sound and its approximation
sound(sig.y,sig.Fs);
%%
sound(r2,sig.Fs);
%% Same, but this time add a deadzone of 3 samples around basis functions
[ws2,r2] = temporalMP(sig.y,gabors,true,5000,0,3);
%%
subplot(3,1,1);
plot(gabors);
title('Basis');
subplot(3,1,2);
plot([sig.y,r2]);
legend('signal','approximation');
subplot(3,1,3);
%the convolution here is to make the spikes visible
imagesc(conv2(ws2,exp(-rg.^2/2/20^2),'same')');
ylabel('increasing time ->');
ylabel('increasing frequency ->');
title(sprintf('weights (%d non-zero weights)',nnz(ws(:))));
%%
%Demonstration of deadzone
[t,~] = find(ws2~=0);
min(diff(sort(t)))
%Should be 3
%%
%listen to the original sound and its approximation
sound(sig.y,sig.Fs);
%%
sound(r2,sig.Fs);
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1]张刘刚.基于匹配追踪(MP)算法的信号自适应分解研究及其应用[D].中南大学,2011.DOI:CNKI:CDMD:2.2010.190196.
[2]彭文杰,张晓玲.基于门限正交匹配追踪(TOMP)的线阵SAR三维成像方法[J].新型工业化, 2013(12):8.DOI:10.3969/j.issn.2095-6649.2013.12.008.
[3]秦晓伟,郭建中.匹配追踪算法(MP)在超声成像中的研究[C]//西安-上海市声学学会声学学术会议.2011.
🌈4 Matlab代码实现
相关文章:

【对于一维信号的匹配】对一个一维(时间)信号y使用自定义基B执行匹配追踪(MP)研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
【Oracle 数据库 SQL 语句 】积累1
Oracle 数据库 SQL 语句 1、分组之后再合计2、显示不为空的值 1、分组之后再合计 关键字: grouping sets ((分组字段1,分组字段2),()) select sylbdm ,count(sylbmc) a…...

Django中级指南:理解并实现Django的模型和数据库迁移
Django 是一个极其强大的 Python Web 框架,它提供了许多工具和特性,能够帮助我们更快速、更便捷地构建 Web 应用。在本文中,我们将会关注 Django 中的模型(Models)和数据库迁移(Database Migrations&#x…...

Chatgpt API调用报错:openai.error.RateLimitError
Chatgpt API 调用报错: openai.error.RateLimitError: You exceeded your current quota, please check your plan and billing details. 调用OpenAI API接口 import openai import osopenai.api_key os.getenv("OPENAI_API_KEY")result openai.Chat…...

一键获取数百张免费商用人脸!AI人脸生成器来袭
随着科技的发展,人工智能正在渗透到生活的各个角落,设计行业也不例外。在网页、APP、PPT 等界面设计中,设计师经常需要插入真实的人脸素材,以增强作品的真实感和场景化。但是获取素材既不容易,质量和价格也难免成为设计…...

跳跃游戏 II——力扣45
文章目录 题目描述解法一 贪心题目描述 解法一 贪心 int jump(vector<int>& nums){in...

Stable Diffusion - 常用的负向提示 Embeddings 解析与 坐姿 (Sitting) 提示词
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://spike.blog.csdn.net/article/details/132145248 负向 Embeddings 是用于提高 StableDiffusion 生成图像质量的技术,可以避免生成一些不符合预期的图像特征,比如…...
:C#实现指南)
工厂方法模式(一):C#实现指南
工厂方法模式是一种创建型设计模式,用于处理对象的创建问题。通过使用工厂方法模式,我们可以将对象的创建过程与使用过程分离,从而增加代码的灵活性和可维护性。 工厂方法模式的定义 工厂方法模式定义了一个创建对象的接口,但由子…...

Spring接口InitializingBean的作用和使用介绍
在Spring框架中,InitializingBean接口是一个回调接口,用于在Spring容器实例化Bean并设置Bean的属性之后,执行一些自定义的初始化逻辑。实现InitializingBean接口的Bean可以在初始化阶段进行一些必要的操作,比如数据的初始化、资源…...
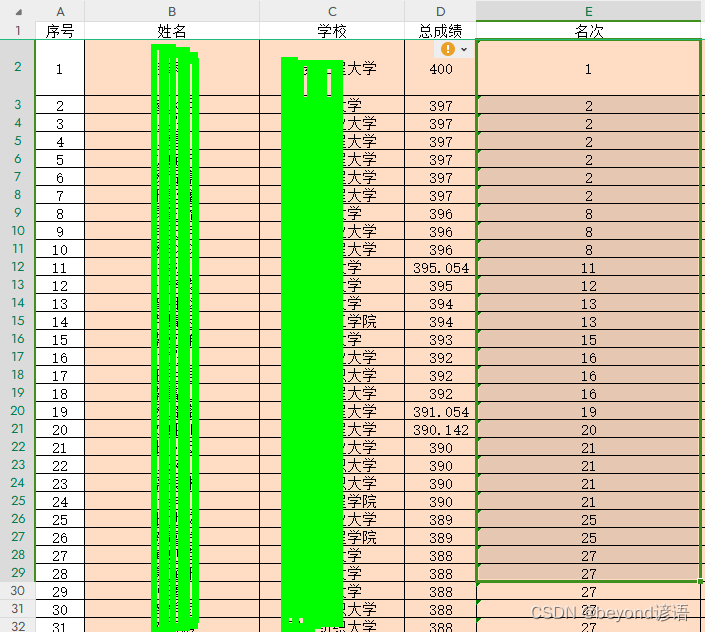
Excel---成绩相同者,名次并列排列,三步搞定
需求:一张成绩表,共341行(340条数据,第一条为标题),根据成绩进行排序,成绩相同进行名次并列 一、选择生成结果的位置,我这里点击了一下E2单元格 二、公式—>插入–>rank函数 数值:D2 表示…...

Elasticsearch6.x和7.x的区别
Elasticsearch6.x和7.x的区别 1、查找方面的区别 在增删改方面,6.x和7.x是一样的,在查找方面(分为普通查找和有高亮的查找),6.x和7.x有区别。 在7.x的es中: org.springframework.data.elasticsearch.cor…...

基于STM32设计的口罩识别和无线测温系统
一、设计需求 基于STM32设计的口罩识别和无线测温系统 1.1 项目背景 随着深度学习和计算机视觉的快读发展,与此有关的技术设备已经被大幅度的使用,并且不仅仅在这两个方面,更在许许多多的领域都有使用。众所周知,图像理解之中的最重要的一个步骤即为目标检测,和为目标检测…...

第五十天
●软件测试的目的 软件测试的目的是寻找错误,并且尽可能找出更多的错误。 测试是程序的执行过程,目的在于发现错误 一个好的测试用例在于能够发现至今为止未发现的错误 一个成功的测试是发现了至今未发现的错误的测试 ●软件测试工作流程࿱…...

vue-pc端elementui-统一修改问题-Dialog 对话框点击空白关闭问题-element-所有组件层级问题
前言 实际开发我们经常发现dialog弹出框默认点击遮罩层空白地方就会关闭-有属性可以关闭 但是经常会图方便-或者已经写完了,不想一个个写,可以在main.js进行统一关闭 当我们在页面进行复杂设计和层级关闭改变,会发现右上角的退出登录弹出款…...
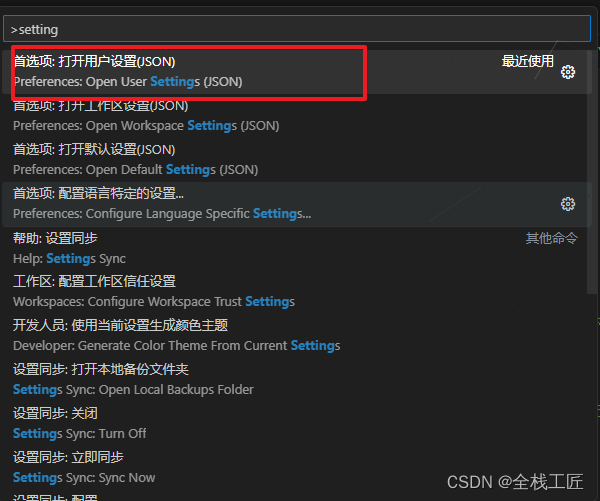
VS code 用户设置
ctrlshiftP打开用户设设置 vscode user setting.json 中的配置 {// vscode默认启用了根据文件类型自动设置tabsize的选项"editor.detectIndentation": false,//黄色波浪线"eslint.enable": false,// 重新设定tabsize"editor.tabSize": 2,&quo…...

【Spring security 解决跨域】
security 跨域 概述方案方案一方案二方案三方案四 主页传送门:📀 传送 概述 Spring Security是一个功能强大且高度可定制的,主要负责为Java程序提供声明式的身份验证和访问控制的安全框架。其前身是Acegi Security,后来被收纳为Spring的一个…...
【C语言】经典题目(四)
HI,大家好~😝😝这是一篇C语言经典题目的博客。 更多C语言经典题目及刷题篇,可以参考: 🌸 【C语言】经典题目(一) 🌸 【C语言】经典题目(二) 🌸 【C语言】经典题目(三) 🌸…...

Prometheus-监控 Postgresql
一、部署 1 二进制方式部署 github 地址:https://github.com/prometheus-community/postgres_exporter 1.1 下载 可以从官方发布版本中找到多个平台的二进制安装包。 打开连接后,点击 Assets,即可看到下载列表。 本文档使用如下版本作为示例 curl -o postgres_exporte…...

Android java.lang.UnsatisfiedLinkError: No implementation found
例如,该项目的如下报错: java.lang.UnsatisfiedLinkError: No implementation found for void org.webrtc.PeerConnectionFactory.nativeInitializeAndroidGlobals() (tried Java_org_webrtc_PeerConnectionFactory_nativeInitializeAndroidGlobals and…...

Leecode力扣704数组二分查找
题目链接为:https://leetcode.cn/problems/binary-search/ 最终代码为: class Solution { public:int search(vector<int>& nums, int target) {int begin 0;int end nums.size() - 1;while (begin < end) {int mid (begin end) / 2;…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

