121. 买卖股票的最佳时机
题目描述
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
1 <= prices.length <= 1050 <= prices[i] <= 104
解答
class Solution {
public:int maxProfit(vector<int>& prices) {// 贪心法取最左最小值和最右最大值int low = INT_MAX;int res = 0;for(int i = 0; i < prices.size(); ++i){low = min(low, prices[i]);res = max(res, prices[i] - low);} return res;}int maxProfit1(vector<int>& prices) {// dp[i][0] 表示第i天持有可获得的最大利润// dp[i][1] 表示第i天不持有可获得的最大利润vector<vector<int>> dp(prices.size(), vector<int>(2, 0));// 第i天持有股票所得最多现金dp[i][0]有两种情况// case1:第i-1天就持有,则保持现状为 dp[i - 1][0]// case1:第i-1天未持有,则当天买入 -prices[i]// 得 dp[i][0] = max(dp[i - 1][0], - prices[i]);// 第i天不持有股票所得最多现金dp[i][1]有两种情况// case1:第i-1天持有,则当天卖出 dp[i - 1][0] + prices[i]// case1:第i-1天未持有,则保持现状 dp[i - 1][1]// 故得:dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);dp[0][0] = -prices[0];dp[0][1] = 0;for(int i = 1; i < prices.size(); ++i){dp[i][0] = max(dp[i - 1][0], -prices[i]);dp[i][1] = max(dp[i - 1][0] + prices[i], dp[i - 1][1]);}// 最后一天不持有所得最大现金return dp[prices.size() - 1][1];}
};
相关文章:

121. 买卖股票的最佳时机
题目描述 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。 返回你可以从这笔交易中获取的…...
 LTO(Link-Time Optimization))
FDO(Feedback-Driven Optimization) LTO(Link-Time Optimization)
反馈驱动优化(Feedback-Driven Optimization,FDO)和链接时优化(Link-Time Optimization,LTO)是两种重要的编译器优化技术。下面我们详细介绍这两种技术: 反馈驱动优化 (FDO): FDO 是…...

低成本无刷高速吹风机单片机方案
高速吹风机的转速一般是普通吹风机的5倍左右。一般来说,吹风机的电机转速一般为2-3万转/分钟,而高速吹风机的电机转速一般为10万转/分钟左右。高转速增加了高风速。一般来说,吹风机的风力只有12-17米/秒,而高速吹风机的风力可以达…...

使用Python爬取某查查APP端(Appium自动化篇)
1. 写在前面 某查查网站反爬虫风控还是较强的,之后会分别介绍一下PC端协议、APP端自动化、APP端接口协议三种采集方案。这里主要介绍APP端的自动化方式,APP端自动化方式需要登陆账号,协议的话需要签名授权(自动化经测试没有太多限…...

vue3实现组件可拖拽 vuedraggable
npm i -S vuedraggablenext 中文文档,里面有完整代码案例,值得一看 vue.draggable vue3 版本在工作台中的应用场景 - itxst.com...

gradio常用组件
gradio常用组件 1.gradio程序启动2.写入html相关代码3.文本框4. 回车触发事件5.选择按钮框6.下拉框7.点击按钮8.清空按钮9.监听组件10.输出流11.template 1.gradio程序启动 import gradio as gr def tab():pass with gr.Blocks() as ui:gr.Markdown("# <center>&am…...
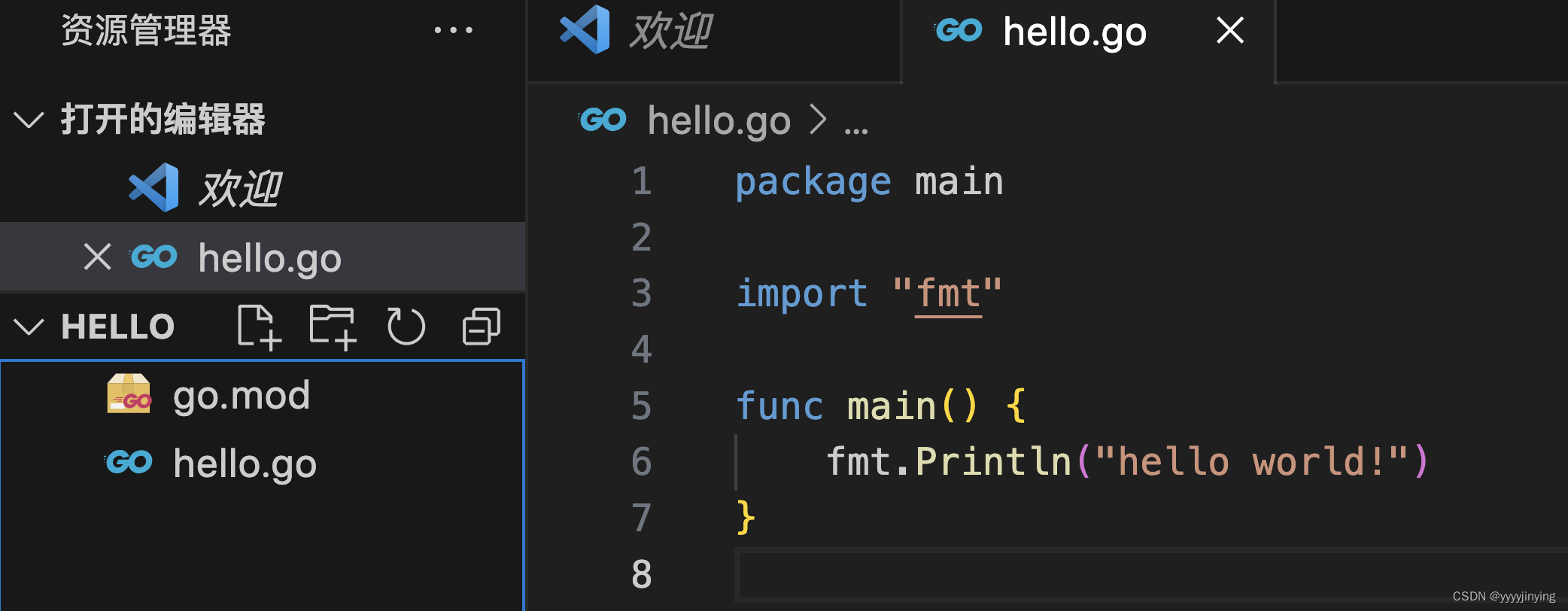
vcode开发go
配置环境变量 go env -w GO111MODULEon go env -w GOPROXYhttps://goproxy.cn,direct 创建文件夹 mkdir hello cd hello go mod help go mod help 初始化一个项目 go mod init hello 获取第三方包 go get github.com/shopspring/decimal 将依赖包下载到本地 go mod …...

聊城大学823软件工程考研
1.什么是软件工程?它目标和内容是什么? 软件工程就是用科学的知识和技术原理来定义,开发,维护软件的一门学科。 软件工程目标:付出较低开发成本;达到要求的功能;取得较好的性能;开发的软件易于移植&…...
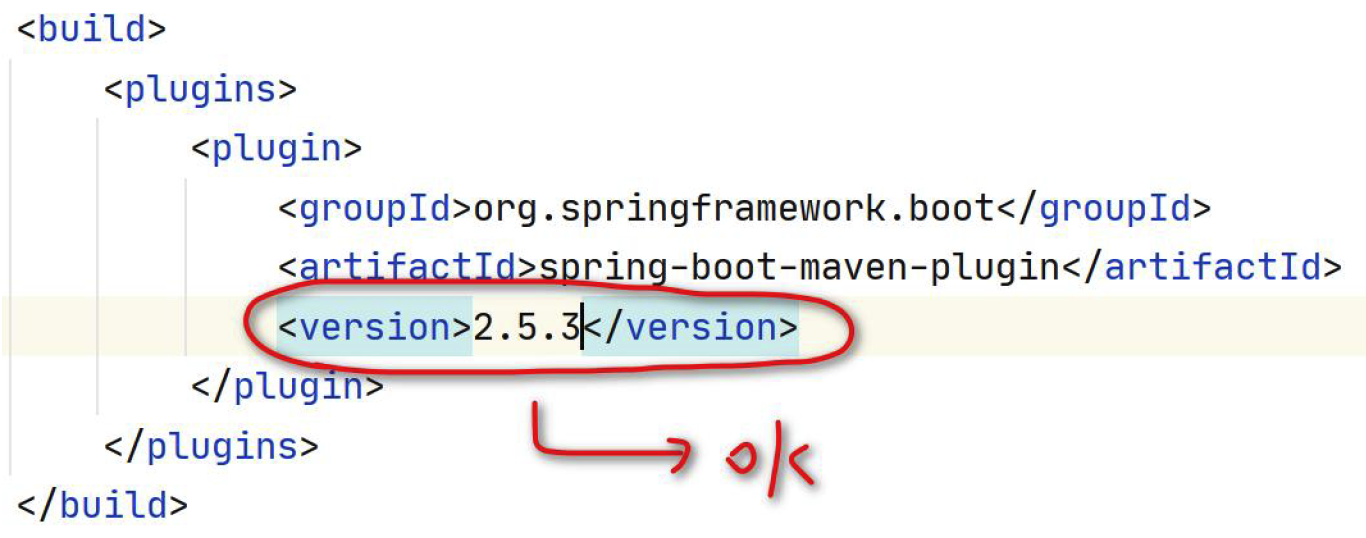
Spring Initailizr--快速入门--SpringBoot的选择
😀前言 本篇博文是关于IDEA使用Spring Initializer快速创建Spring Boot项目的说明,希望能够帮助到您😊 🏠个人主页:晨犀主页 🧑个人简介:大家好,我是晨犀,希望我的文章可…...

大数据课程I1——Kafka的概述
文章作者邮箱:yugongshiye@sina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 了解Kafka的概念; ⚪ 掌握Kafka的配置与启动; 一、简介 1. 基本概念 Apache kafka 是一个分布式数据流平台。可以从如下几个层面来理解: 1. 我们可以向Kafka发布数据以及从Kafka订阅…...

视图簇 se54 sm34 se54
今天演练了一下 维护视图到视图簇的过程。 se11建表,建表之后 【使用程序】→【表维护生成器】 se54 新建视图簇 对象结构 选中其中一行 字段附属 PS:以上每一行都要设置过去 , 设置完成了 激活 sm34展示...

风丘科技将亮相 EVM ASIA 2023
风丘科技将首次亮相 EVM ASIA 2023 WINDHILL will debut EVM ASIA 2023 ——可持续移动的未来 —The Future of SUSTAINABLE Mobility EVM ASIA 2023是亚太地区电气化的国际性展会,专注于新能源汽车、充电技术及汽车零件制造等。展会致力于促进包括充电站、交通…...

腾讯云服务器S6、SA3、S5、SA2等CVM实例介绍
腾讯云服务器CVM实例标准型S6、SA3、S5、SA2等多款实例降价,最高幅度达40%,标准型S6云服务器是新一代云服务器,SA3和SA2是AMD处理器,标准型S5是次新一代的云服务器,如下图: 腾讯云服务器CVM降价 标准型S6&a…...

使用kickstart和anaconda自动化安装centos系统
使用kickstart和anaconda自动化安装centos系统 使用kickstart和anaconda自动化安装centos系统 anaconda 介绍 kickstart 介绍 实验过程 前提 1.已经安装好至少两台centos系统 2.需要实现自动安装的系统的光盘镜像 3.已安装的系统之间可以通讯(比如处于VMware中的NAT网络的…...
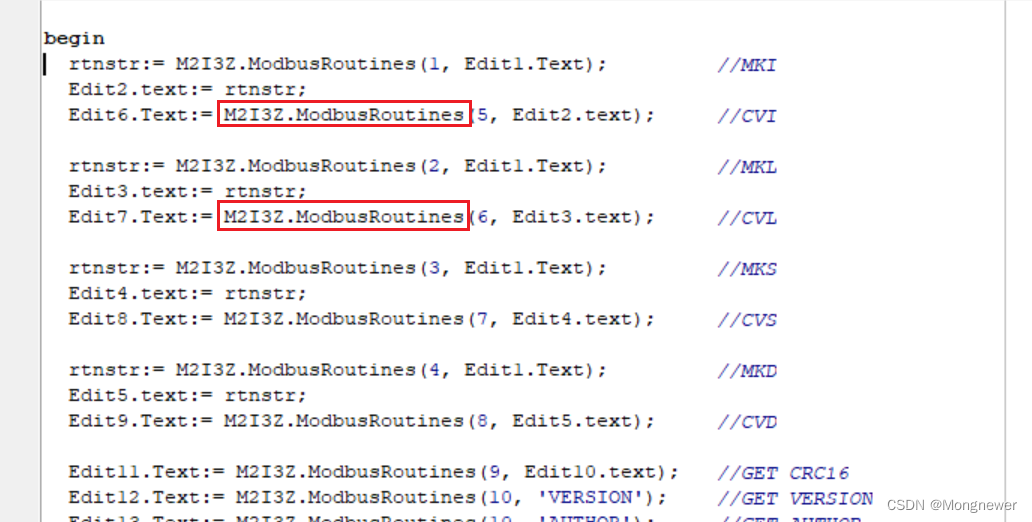
Delphi7通过VB6之COM对象调用PowerBASIC写的DLL功能
Delphi7通过VB6之COM对象调用PowerBASIC写的DLL功能。标题挺长,其实目标很简单,就是在Delphi7中使用PowerBASIC的MKI/CVI, MKS/CVS, MKD/CVD,并顺便加入CRC16检验函数,再进行16进制高低字节调整,方便在VB6、Delphi、La…...

中电金信:ChatGPT一夜爆火,知识图谱何以应战?
随着ChatGPT的爆火出圈 人工智能再次迎来发展小高潮 那么作为此前搜索领域的主流技术 知识图谱前路又将如何呢? 事实上,ChatGPT也并非“万能”,作为黑箱模型,ChatGPT很难验证生成的知识是否准确。并且ChatGPT是通过概率模型执行推…...

单细胞分类和预测任务
对于分类和预测任务,在生物信息学领域有一些常用的方法和工具可以使用。以下是一些常见的方法和工具: 1. 机器学习方法: 包括支持向量机(Support Vector Machine,SVM)、随机森林(Random Forest…...

那些年的Webview开发经验记录
获取网站视频真实链接 直接上工具类 直接调用即可,这个工具类会返回加载的网页中所有的链接,至于对链接怎么处理就是你们自己的事了, 亲测至今我所遇到的所有视频,它都可以捕获到其链接 import android.app.Activity; import an…...

ssh-keygen详解
ssh-keygen命令参数详解 -b BITS指定密钥长度。 -e读取私有或公共 OpenSSH 密钥文件并以 -m 选项指定的格式之一将密钥打印到标准输出。 -C添加注释。 -f FILENAME指定用来保存密钥的文件名。 -i以 -m 选项指定的格式读取未加密的私钥(或公钥)文件&…...
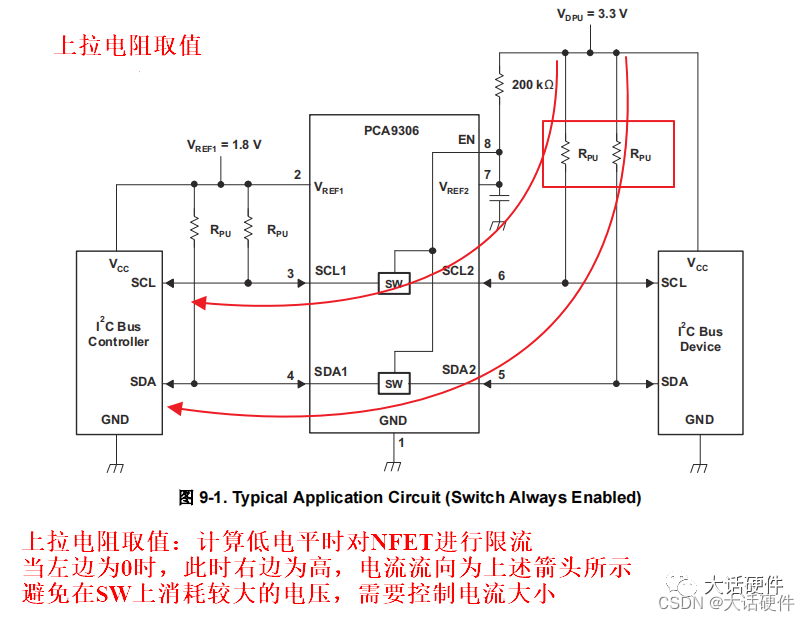
自动方向识别式 LSF型电平转换芯片
大家好,这里是大话硬件。 今天这篇文章想分享一下电平转换芯片相关的内容。 其实在之前的文章分享过一篇关于电平转换芯片的相关内容,具体可以看链接《高速电路逻辑电平转换设计》。当时这篇文章也是分析的电平转换芯片,不过那时候更多的是…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...
