二叉树的相关列题!!
对于二叉树,很难,很难!笔者也是感觉很难!虽然能听懂课程,但是,对于大部分的练习题并不能做出来!所以感觉很尴尬!!因此,笔者经过先前的那篇博客,已经开启了大脑奇迹!!现在还热乎着!刚刚的更文!!二叉树讲解https://blog.csdn.net/weixin_64308540/article/details/129046267?spm=1001.2014.3001.5501
言归正传,这篇文章,主要在于二叉树的相关列题!!大概也就十来个!但是,基本每个都有代码+思路,还有一些瞎扯白,那就确实不容易了!!
100. 相同的树
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
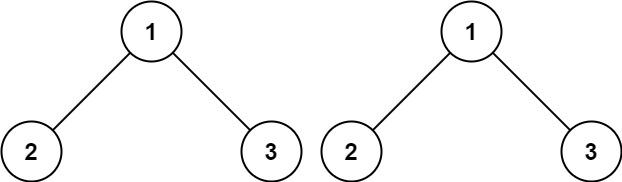
输入:p = [1,2,3], q = [1,2,3]
输出:true
示例 2:
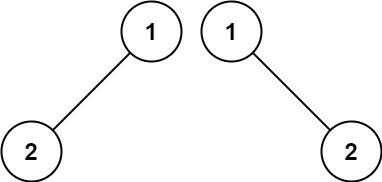
输入:p = [1,2], q = [1,null,2]
输出:false
示例 3:
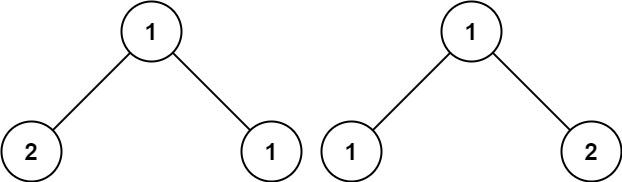
输入:p = [1,2,1], q = [1,1,2]
输出:false
提示:
两棵树上的节点数目都在范围 [0, 100] 内
-104 <= Node.val <= 104
根据上述的题目,我们可以得出:
如果根节点相同,则判断左节点是否相同,继而判断右节点是否相同!
那么何为相同呢??对于相同不相同,我们有着一下的感想:
结构(为空,不为空)(1)一个为空,一个不为空,(2)两个都为空,(3)2个都不为空(不一定,还得看val值)
值(val)
根据上述的思考,我们可以有着下述的简单代码
//判断两个树是否相同!public boolean isSameTree(TreeNode p,TreeNode q){if (p==null && q !=null || p !=null && q==null){return false;}//此时,p,q 要不都是空,要不都不是空if (p==null && q==null){return true;//都为空树,此时也相同}if (p.val !=q.val){return false;//都不是空,且值不相同的情况下!}//此时,p,q都不是空,且根节点一样,那么,继续判断左子树/右子树return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);}这个代码,看着很简单,但是,写起来,容易缺少思路!!
感兴趣的可以思考一下时间复杂度与空间复杂度!!
572. 另一棵树的子树
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
示例 1:
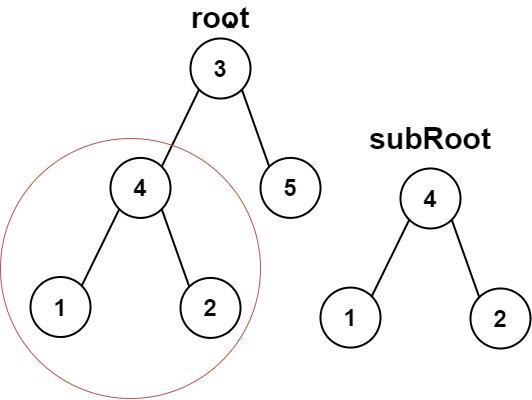
输入:root = [3,4,5,1,2], subRoot = [4,1,2]
输出:true
示例 2:
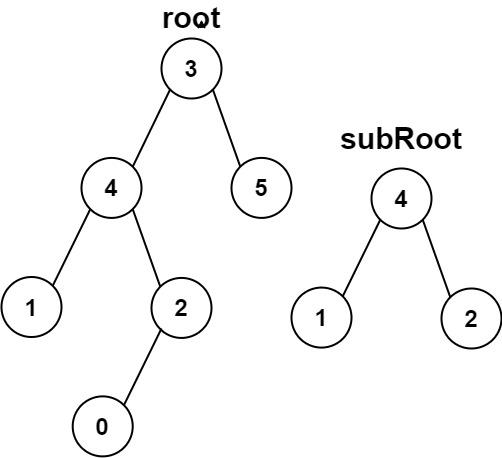
输入:root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
输出:false
提示:
root 树上的节点数量范围是 [1, 2000]
subRoot 树上的节点数量范围是 [1, 1000]
-104 <= root.val <= 104
-104 <= subRoot.val <= 104
根据上述题目的案列,我们可以得出思路:是不是相同的树??是不是root的左子树??是不是root的右子树??那么,我们可以有着下述的代码:
//判断两个树是否相同!public boolean isSameTree(TreeNode p,TreeNode q){if (p==null && q !=null || p !=null && q==null){return false;}//此时,p,q 要不都是空,要不都不是空if (p==null && q==null){return true;//都为空树,此时也相同}if (p.val !=q.val){return false;//都不是空,且值不相同的情况下!}//此时,p,q都不是空,且根节点一样,那么,继续判断左子树/右子树return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);}//另一颗子树public boolean isSubTree(TreeNode root,TreeNode subRot){if (root==null ||subRot==null){return false;}if (isSameTree(root,subRot)){return true;}if (isSameTree(root.left,subRot)){return true;}if (isSameTree(root.right,subRot)){return true;}return false;}该段代码,我们借助是不是相同的树的代码了!!显得我们有点儿投机取巧了!!
感兴趣的读者,可以思考一下时间复杂度与空间复杂度!
226. 翻转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
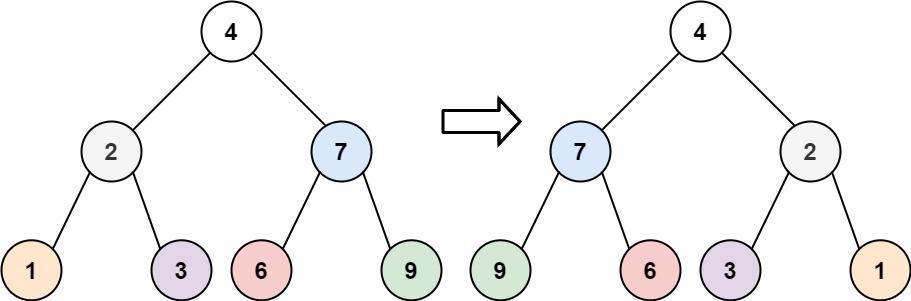
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
示例 2:
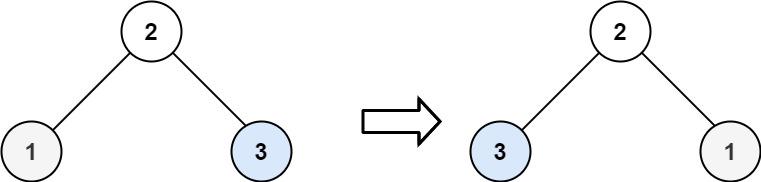
输入:root = [2,1,3]
输出:[2,3,1]
示例 3:
输入:root = []
输出:[]
提示:
树中节点数目范围在 [0, 100] 内
-100 <= Node.val <= 100
对于实列中的代码,我们可以看出:
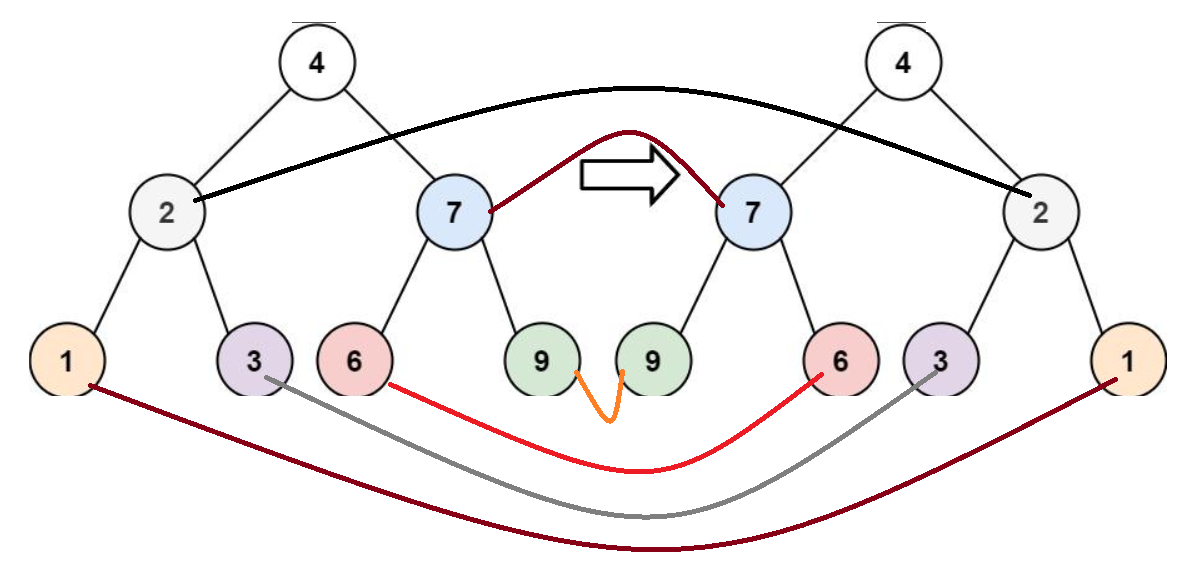
最后得出:root的左子树和root的右子树实现了交换!!(交换的是左右两个子树,而不是仅仅交换哪个节点)
参考代码:
//翻转二叉树public TreeNode invertTree(TreeNode root){if (root==null){return null;}TreeNode tmp=root.left;root.left=root.right;root.right=tmp;invertTree(root.left);invertTree(root.right);return root;}110. 平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
示例 1:
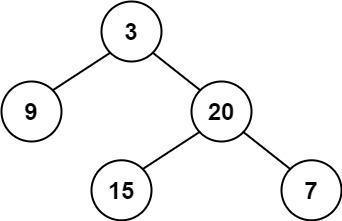
输入:root = [3,9,20,null,null,15,7]
输出:true
示例 2:
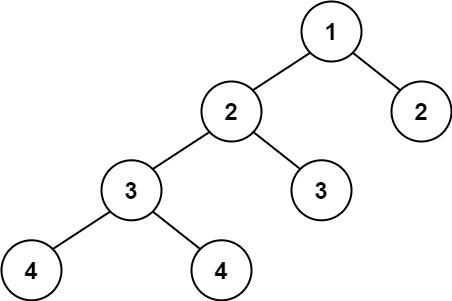
输入:root = [1,2,2,3,3,null,null,4,4]
输出:false
示例 3:
输入:root = []
输出:true
提示:
树中的节点数在范围 [0, 5000] 内
-104 <= Node.val <= 104
对于该题目,我们可以看出:左右高度差不超过1(每个节点都要求高度)
写法1:
//平衡二叉树public boolean isBalanced(TreeNode root){if (root==null){return true;}int leftH=maxDepth(root.left);int rightH=maxDepth(root.right);return Math.abs(leftH-rightH)<2 &&isBalanced(root.left)&&isBalanced(root.right);}//求树的高度public int maxDepth(TreeNode root){if (root==null){return 0;}int leftHeight=maxDepth(root.left);int rightHeight=maxDepth(root.right);return (leftHeight > rightHeight) ? (leftHeight+1) : (rightHeight+1);}对于这个题目,我们会是感觉很难!很难!而且时间复杂度很大很大!在力扣上面直接跑不过!!(超时),该时间复杂度为O(n^2),那么,我们是否可以写一个时间复杂度为O(n)的呢?请看下述的代码:
写法2:在求高度的过程中,判断是不是平衡二叉树
public boolean isBalanced2(TreeNode root){return maxDepth2(root)>0;}public int maxDepth2(TreeNode root){if (root==null){return 0;}int leftHeight=maxDepth2(root.left);int rightHeight=maxDepth2(root.right);if (leftHeight>=0 && rightHeight>=0 && Math.abs(leftHeight-rightHeight)<=1){return Math.max(leftHeight,rightHeight)+1;//求最大值}else {return -1;//不平衡,返回一个负数}}101. 对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
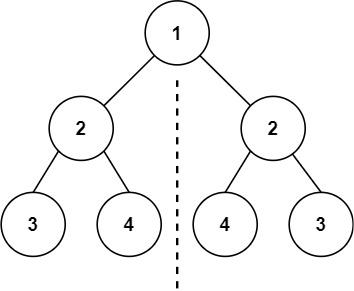
输入:root = [1,2,2,3,4,4,3]
输出:true
示例 2:
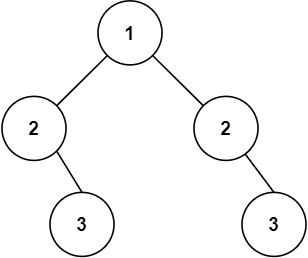
输入:root = [1,2,2,null,3,null,3]
输出:false
提示:
树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100
根据题意,我们可以看出:判断这棵树是不是轴对称的!主要在于判断这棵树的左子树和这棵树的右子树是否对称??
判断方法:
判断左子树的左树和右子树的右树
判断左子树的右树和右子树的左树
参考代码为:
//对称二叉树public boolean isSymmetric(TreeNode root){if (root==null){return true;//判断根节点是否为空}return isSymmetricChild(root.left,root.right);}public boolean isSymmetricChild(TreeNode leftTree,TreeNode rightTree){if (leftTree != null && rightTree==null || leftTree==null && rightTree !=null){return false;//一个为空,一个不为空}if (leftTree==null && rightTree==null){return true;//两个都为空}if (leftTree.val != rightTree.val){return false;}//判断左子树的左树和右子树的右树//判断左子树的右树和右子树的左树return isSymmetricChild(leftTree.left,rightTree.right)&&isSymmetricChild(leftTree.right,rightTree.left);}102. 二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
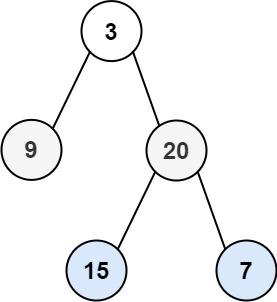
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
提示:
树中节点数目在范围 [0, 2000] 内
-1000 <= Node.val <= 1000
对于这个题目,我们可以考虑用队列!!队列的先进先出模式,符合一层层遍历的逻辑!!
写法1:
//二叉树的层序遍历public void levelOrder(TreeNode root){if (root==null){return;}//队列Queue<TreeNode> queue=new LinkedList<>();queue.offer(root);//先把根节点放在队列里while ( !queue.isEmpty()){//当前队列不为空TreeNode cur=queue.poll();//弹出(出队列)System.out.print(cur.val+" ");if (cur.left !=null){queue.offer(cur.left);//入队列}if (cur.right !=null){queue.offer(cur.right);}}}写法2:
public List<List<Integer>> levelOrder2(TreeNode root){List<List<Integer>> list=new ArrayList<>();if (root==null){return list;}Queue<TreeNode> queue=new LinkedList<>();queue.offer(root);while ( !queue.isEmpty()){int size=queue.size();List<Integer> tmp=new ArrayList<>();while (size!=0){TreeNode cur=queue.poll();size--;if (cur.left !=null){queue.offer(cur.left);}if (cur.right !=null){queue.offer(cur.right);}}list.add(tmp);}return list;}对于写法2 ,其实还是使用了二维数组!!二维数组!!对于这个写法,其实我在之前的杨辉三家中有过具体的描述,若是不懂得各位老铁,可以翻一下笔者之前的博客,或者来咨询一下笔者!!
KY11 二叉树遍历
描述
编一个程序,读入用户输入的一串先序遍历字符串,根据此字符串建立一个二叉树(以指针方式存储)。 例如如下的先序遍历字符串: ABC##DE#G##F### 其中“#”表示的是空格,空格字符代表空树。建立起此二叉树以后,再对二叉树进行中序遍历,输出遍历结果。
输入描述:
输入包括1行字符串,长度不超过100。
输出描述:
可能有多组测试数据,对于每组数据, 输出将输入字符串建立二叉树后中序遍历的序列,每个字符后面都有一个空格。 每个输出结果占一行。
示例1
输入:
abc##de#g##f###
复制
输出:
c b e g d f a
根据题目的这个案列,我们可以创建一棵二叉树!
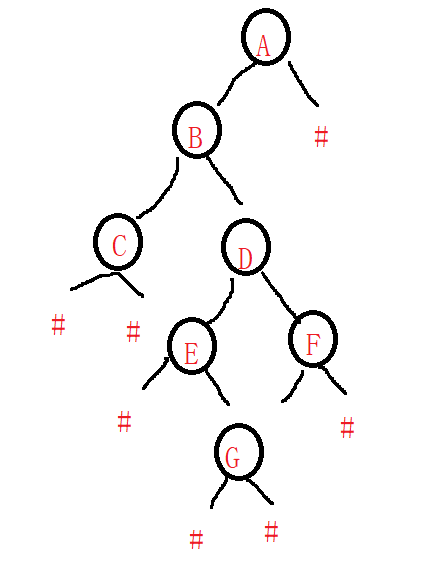
那么,我们可以有着一下所示的代码:
import java.util.Scanner;public class TreeNode {public char val;public TreeNode left;public TreeNode right;//构造方法public TreeNode(char val) {this.val = val;}public static void main(String[] args) {Scanner in =new Scanner(System.in);while (in.hasNextLine()){String str=in.nextLine();//定义root接收这个树的节点TreeNode root=creatrTree(str);inorder(root);//中序遍历}}public static int i=0;//i不会越界,有递归次数的限制public static TreeNode creatrTree(String str){TreeNode root=null;if (str.charAt(i) != '#'){//根左右root=new TreeNode(str.charAt(i));i++;root.left=creatrTree(str);//左数root.right=creatrTree(str);//右数}else {i++;}return root;}//中序遍历public static void inorder(TreeNode root){if (root==null){return;}inorder(root.left);//左System.out.print(root.val+" ");//根inorder(root.right);//右}
}
236. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
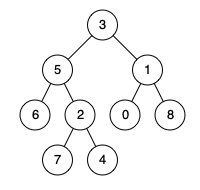
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。示例 2:
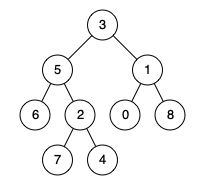
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。示例 3:
输入:root = [1,2], p = 1, q = 2
输出:1
提示:
树中节点数目在范围 [2, 105] 内。
-109 <= Node.val <= 109
所有 Node.val 互不相同 。
p != q
p 和 q 均存在于给定的二叉树中。
对于上述的题目,我们可以得出一下思考:
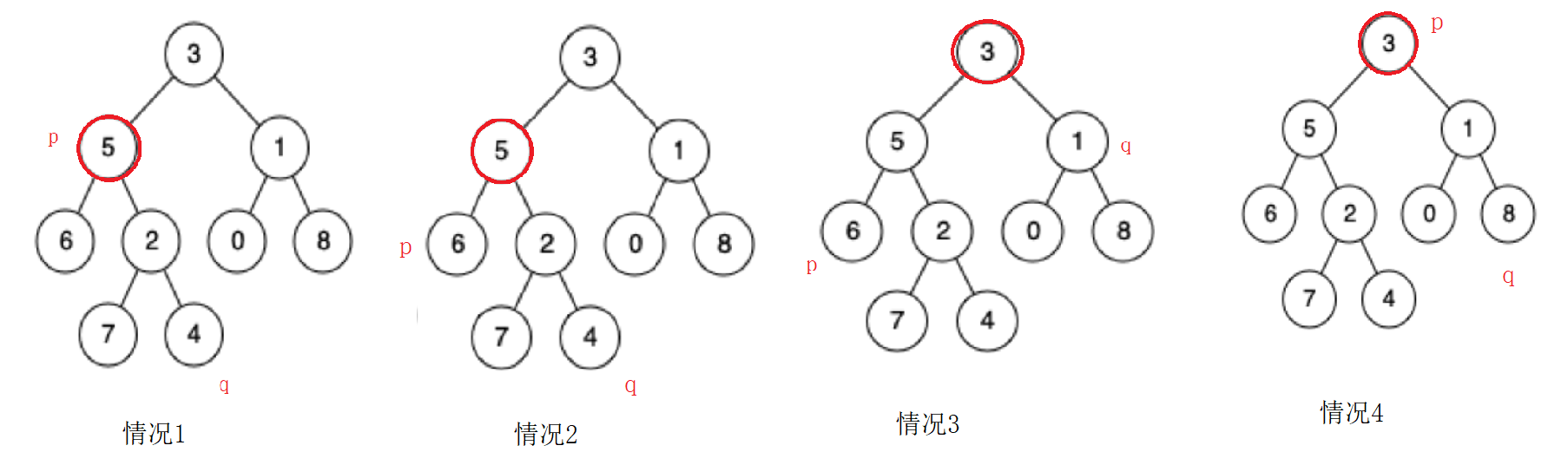
因此:
要么在根的左右两边
要么在根的左边或者右边
要么在根的左边或者右边,其中一个节点是公共祖先
那么,我们可以有着一下 的代码:
//二叉树的最近公共祖先public TreeNode lowestCommonAncestor(TreeNode root,TreeNode p,TreeNode q){if (root==null){return null;}//先判断根节点是否为其中一个?if (root==p || root==q){return root;}//左边找找?TreeNode leftRet=lowestCommonAncestor(root.left,p,q);//右边找找?TreeNode rightRet=lowestCommonAncestor(root.right,p,q);if (leftRet!=null && rightRet !=null){return root;//左右两边都找到了}else if (leftRet!=null){return leftRet;//左边找到了}else if (rightRet!=null){return rightRet;//右边找到了}return null;}105. 从前序与中序遍历序列构造二叉树
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:
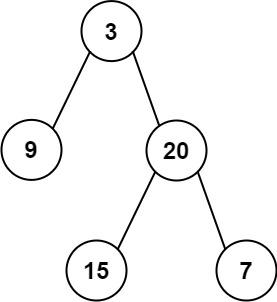
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]
提示:
1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证 为二叉树的前序遍历序列
inorder 保证 为二叉树的中序遍历序列
首先,我们需要知道的是:前序遍历的第一个节点是根节点!!中序遍历找到根节点,左侧的是左树,右侧的是右树!!
那么,我们可以有着下述的简单代码:
//从前序遍历与中序遍历,构造二叉树
public class Solution {class TreeNode{int val;TreeNode left;TreeNode right;TreeNode(){}public TreeNode(int val) {this.val = val;}public TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}}int i=0;public TreeNode buildTree(int[] preorder , int[] inorder){return buildTreeChild(preorder,inorder,0,inorder.length-1);}//preorder前序遍历//inorder中序遍历public TreeNode buildTreeChild(int[] preorder,int[] inorder,int inbegin,int inend){if (inbegin > inend){return null;//没有子树}TreeNode root =new TreeNode(preorder[i]);int rootIndex=findIndex(inorder,inbegin,inend,preorder[i]);i++;root.left=buildTreeChild(preorder,inorder,inbegin,rootIndex-1);root.right=buildTreeChild(preorder,inorder,rootIndex+1,inend);return root;}private int findIndex(int[] inorder,int inbegin,int inend,int key){for (int i = 0; i <= inend; i++) {if (inorder[i]==key){return i;}}return -1;}
}代码有点儿复杂,大家自求多福!!
106. 从中序与后序遍历序列构造二叉树
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:
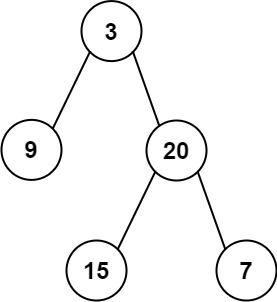
输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出:[3,9,20,null,null,15,7]
示例 2:
输入:inorder = [-1], postorder = [-1]
输出:[-1]
提示:
1 <= inorder.length <= 3000
postorder.length == inorder.length
-3000 <= inorder[i], postorder[i] <= 3000
inorder 和 postorder 都由 不同 的值组成
postorder 中每一个值都在 inorder 中
inorder 保证是树的中序遍历
postorder 保证是树的后序遍历
//从中序与后序遍历序列构造二叉树
public class Test1 {class TreeNode{int val;Solution.TreeNode left;Solution.TreeNode right;TreeNode(){}public TreeNode(int val) {this.val = val;}public TreeNode(int val, Solution.TreeNode left, Solution.TreeNode right) {this.val = val;this.left = left;this.right = right;}}int i=0;public TreeNode buildTree(int[] inorder,int[] postorder){int i=postorder.length-1;return buildTreeChild2(postorder,inorder,0,inorder.length-1);}public TreeNode buildTreeChild2(int[] postorder,int[] inorder,int inbegin,int inend){if (inbegin>inend){return null;}TreeNode root=new TreeNode(postorder[i]);//找到当前根在中序遍历的位置int rootIndex=findIndex(inorder,inbegin,inend,postorder[i]);i--;root.right=buildTreeChild2(postorder,inorder,rootIndex+1,inend);root.left=buildTreeChild2(postorder,inorder,inbegin,rootIndex-1);return root;}private int findIndex(int[] inorder,int inbegin,int inend,int key){for (int i = 0; i <= inend; i++) {if (inorder[i]==key){return i;}}return -1;}
}
606. 根据二叉树创建字符串
给你二叉树的根节点 root ,请你采用前序遍历的方式,将二叉树转化为一个由括号和整数组成的字符串,返回构造出的字符串。
空节点使用一对空括号对 "()" 表示,转化后需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。
示例 1:
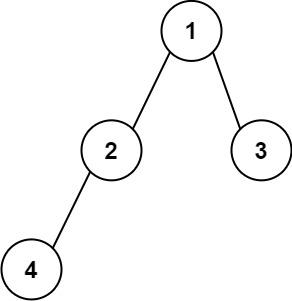
输入:root = [1,2,3,4]
输出:"1(2(4))(3)"
解释:初步转化后得到 "1(2(4)())(3()())" ,但省略所有不必要的空括号对后,字符串应该是"1(2(4))(3)" 。
示例 2:
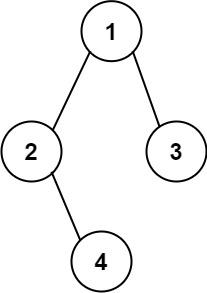
输入:root = [1,2,3,null,4]
输出:"1(2()(4))(3)"
解释:和第一个示例类似,但是无法省略第一个空括号对,否则会破坏输入与输出一一映射的关系。
提示:
树中节点的数目范围是 [1, 104]
-1000 <= Node.val <= 1000
对于该题目,我们可以:
左边为空,右边也为空
左边不为空,右边为空
左边为空,右边不为空
那么,请看笔者的代码:
//根据二叉树创建字符串public String tree2Str(TreeNode root){if (root==null){return null;}//为拼接做准备StringBuilder stringBuilder =new StringBuilder();tree2StrChild(root,stringBuilder);return stringBuilder.toString();//类型转化}//拼接不能用+进行拼接public void tree2StrChild(TreeNode t,StringBuilder stringBulider){if (t==null){return;}stringBulider.append(t.val);//拼接根if (t.left!=null){//左边不为空,加“(”,再递归这颗左树stringBulider.append("(");tree2StrChild(t.left,stringBulider);stringBulider.append(")");//当t.left走完了,回去的时候,加")"}else {//左边空了if (t.right!=null){stringBulider.append("()");}else {//右边为空return;//左边为空,右边也为空}}if (t.right==null){//右边为空return;}else {//右边不为空stringBulider.append("(");tree2StrChild(t.right,stringBulider);//递归右数stringBulider.append(")");}}判断一棵树是不是完全二叉树
完全二叉树:一颗深读为K的有n个节点的二叉树,对树中的节点按从上到下,从左到右的顺序进行编写,如果编号为i(1<=i<=n)的节点,与满二叉树中编号为i的节点在二叉树中的位置相同,那么,这颗二叉树称为完全二叉树!!
//判断一棵树是不是完全二叉树boolean isCompleteTree(TreeNode root){if (root==null){return true;}//借助队列(类似于层序遍历去做Queue<TreeNode> queue=new LinkedList<>();queue.offer(root);while (!queue.isEmpty()){//队列不为空TreeNode cur=queue.poll();//出栈if (cur!=null){queue.offer(cur.left);//入栈queue.offer(cur.right);}else {break;//遇到了null,跳出该循环}}while (!queue.isEmpty()){TreeNode tmp=queue.poll();if (tmp!=null){return false;}}return true;}二叉树的相关列题,便就这么多吧!!但是,当你全部理解的时候,二叉树的知识,已经难不倒你了!!!
相关文章:

二叉树的相关列题!!
对于二叉树,很难,很难!笔者也是感觉很难!虽然能听懂课程,但是,对于大部分的练习题并不能做出来!所以感觉很尴尬!!因此,笔者经过先前的那篇博客,已…...

Java设计模式 - 原型模式
简介 原型模式(Prototype Pattern)是用于创建重复的对象,同时又能保证性能。这种类型的设计模式属于创建型模式,它提供了一种创建对象的最佳方式。 这种模式是实现了一个原型接口,该接口用于创建当前对象的克隆。当直…...

深度学习中的 “Hello World“
Here’s an interesting fact—Each month, there are 186.000 Google searches for the keyword “deep learning.” 大家好✨,这里是bio🦖。每月有超18万的人使用谷歌搜索深度学习这一关键词,是什么让人们对深度学习如此感兴趣?接下来请跟随我来揭开深度学习的神秘面纱。…...

购买WMS系统前,有搞清楚与ERP仓库模块的区别吗
经常有朋友在后台询问我们关于WMS系统的问题,他们自己也有ERP系统,但是总觉得好像还差了点什么,不知道是什么。今天,我想通过本文,来向您简要地阐述ERP与WMS系统在仓储管理上的不同之处。 ERP仓库是以财务为导向的&…...

一文吃透 Spring 中的IOC和DI
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
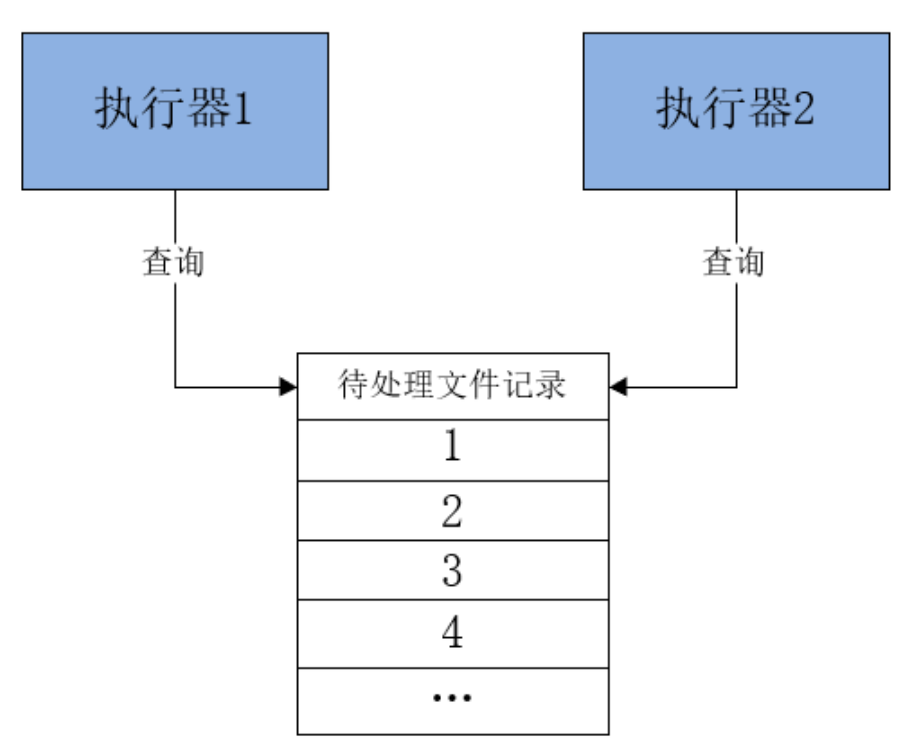
分布式任务处理:XXL-JOB分布式任务调度框架
文章目录1.业务场景与任务调度2.任务调度的基本实现2.1 多线程方式实现2.2 Timer方式实现2.3 ScheduledExecutor方式实现2.4 第三方Quartz方式实现3.分布式任务调度4.XXL-JOB介绍5.搭建XXL-JOB —— 调度中心5.1 下载与查看XXL-JOB5.2 创建数据库表5.3 修改默认的配置信息5.4 启…...

【源码解析】Ribbon和Feign实现不同服务不同的配置
Ribbon服务实现不同服务,不同配置是通过RibbonClient和RibbonClients两个注解来实现的。RibbonClient注册的某个Client配置类。RibbonClients注册的全局默认配置类。 Feign实现不同服务,不同配置,是根据FeignClient来获取自定义的配置。 示…...
【webpack5】一些常见优化配置及原理介绍(二)
这里写目录标题介绍sourcemap定位报错热模块替换(或热替换,HMR)oneOf精准解析指定或排除编译开启缓存多进程打包移除未引用代码配置babel,减小代码体积代码分割(Code Split)介绍预获取/预加载(prefetch/pre…...

力扣sql简单篇练习(十九)
力扣sql简单篇练习(十九) 1 查询结果的质量和占比 1.1 题目内容 1.1.1 基本题目信息 1.1.2 示例输入输出 1.2 示例sql语句 # 用count是不会统计为null的数据的 SELECT query_name,ROUND(AVG(rating/position),2) quality,ROUND(count(IF(rating<3,rating,null))/count(r…...

线段树c++
前言 在谈论到种种算法知识与数据结构的时候,线段树无疑总是与“简单”和“平常”联系起来的。而这些特征意味着,线段树作为一种常用的数据结构,有常用性,基础性和易用性等诸多特点。因此,今天我来讲一讲关于线段树的话题。 定义 首先,线段树是一棵“树”,而且是一棵…...
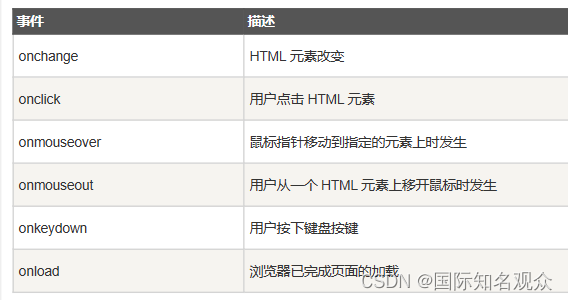
HTML+CSS+JavaScript学习笔记~ 从入门到精通!
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录前言一、HTML1. 什么是HTML?一个完整的页面:<!DOCTYPE> 声明中文编码2.HTML基础①标签头部元素标题段落注释水平线文本格式化②属性3.H…...
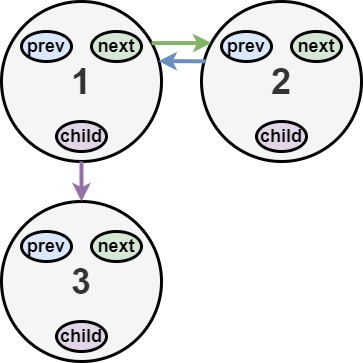
LeetCode 430. 扁平化多级双向链表
原题链接 难度:middle\color{orange}{middle}middle 题目描述 你会得到一个双链表,其中包含的节点有一个下一个指针、一个前一个指针和一个额外的 子指针 。这个子指针可能指向一个单独的双向链表,也包含这些特殊的节点。这些子列表可以有一…...

2.5|iot|第1章嵌入式系统概论|操作系统概述|嵌入式操作系统
目录 第1章: 嵌入式系统概论 1.嵌入式系统发展史 2.嵌入式系统定义* 3.嵌入式系统特点* 4.嵌入式处理器的特点 5.嵌入式处理分类 6.嵌入式系统的应用领域及嵌入式系统的发展趋势 第8章:Linux内核配置 1.内核概述 2.内核代码结构 第1章…...

一文教会你使用ChatGPT画图
引言 当今,ChatGPT在各行各业都有着广泛的应用,其自然语言处理技术也日益成熟。ChatGPT是一种被广泛使用的技术,除了能够生成文本,ChatGPT还可以用于绘图,这为绘图技术的学习和应用带来了新的可能性。本文将介绍如何利用ChatGPT轻松绘制各种形状,为对绘图技术感兴趣的读…...

Java资料分享
随着Java开发的薪资越来越高,越来越多人开始学习 Java 。在众多编程语言中,Java学习难度还是偏高的,逻辑性也比较强,但是为什么还有那么多人要学Java呢?Java语言是目前流行的互联网等企业的开发语言,是市面…...
yum/vim工具的使用
yum 我们生活在互联网发达的时代,手机电脑也成为了我们生活的必须品,在你的脑海中是否有着这样的记忆碎片,在一个明媚的早上你下定决心准备发奋学习,“卸载”了你手机上的所有娱乐软件,一心向学!可是到了下…...
内网渗透(三十九)之横向移动篇-pass the ticket 票据传递攻击(PTT)横向攻击
系列文章第一章节之基础知识篇 内网渗透(一)之基础知识-内网渗透介绍和概述 内网渗透(二)之基础知识-工作组介绍 内网渗透(三)之基础知识-域环境的介绍和优点 内网渗透(四)之基础知识-搭建域环境 内网渗透(五)之基础知识-Active Directory活动目录介绍和使用 内网渗透(六)之基…...

Unity性能优化之纹理格式终极篇
知识早班车:1、当n大于1时,2的n次幂一定能被4整除;证明:2^n 2^2*2^(n-1) 4*2^(n-1)2、4的倍数不一定都是2的次幂;证明:4*3 12;12不是2的次幂3、Pixel(像素)是组成图片…...
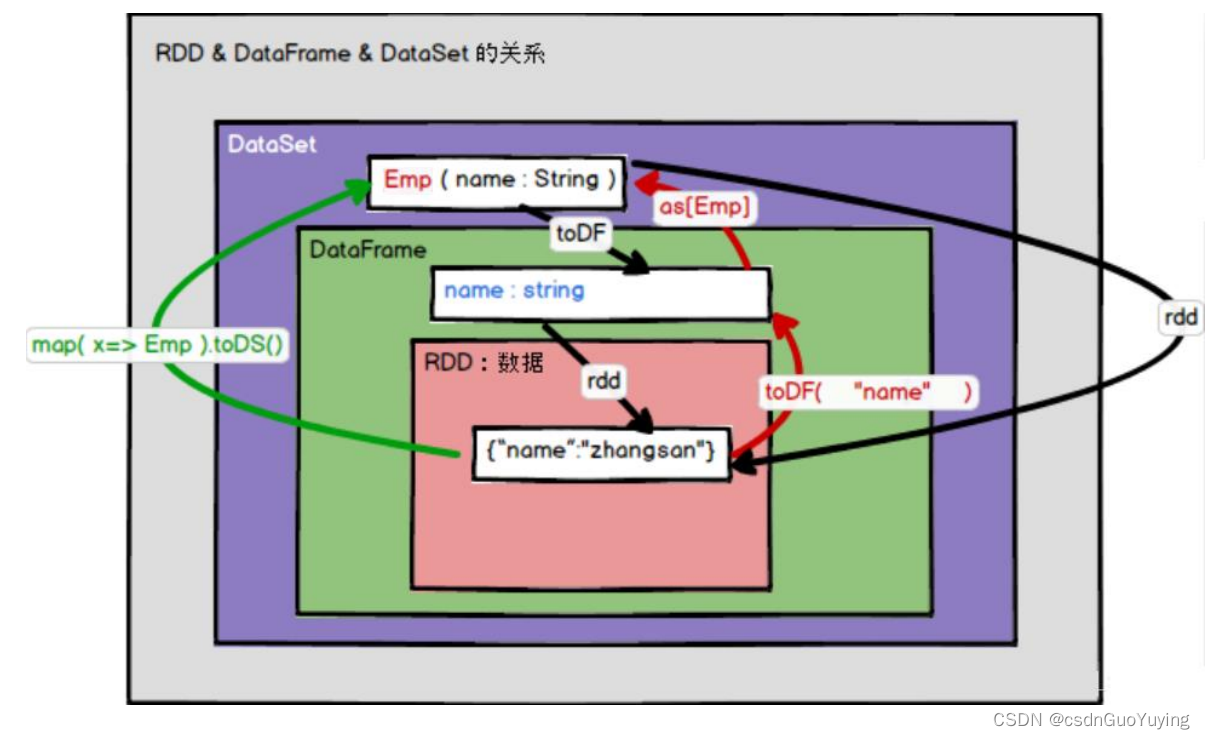
【Spark分布式内存计算框架——Spark SQL】9. Dataset(下)RDD、DF与DS转换与面试题
5.3 RDD、DF与DS转换 实际项目开发中,常常需要对RDD、DataFrame及Dataset之间相互转换,其中要点就是Schema约束结构信息。 1)、RDD转换DataFrame或者Dataset 转换DataFrame时,定义Schema信息,两种方式转换为Dataset时…...

Windows 环境下,cmake工程导入OpenCV库
目录 1、下载 OpenCV 库 2、配置环境变量 3、CmakeLists.txt 配置 1、下载 OpenCV 库 OpenCV官方下载地址:download | OpenCV 4.6.0 下载完毕后解压,便可以得到下面的文件 2、配置环境变量 我们需要添加两个环境变量,一个是 OpenCVConfi…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...
