营销狂人杜国楹的两大顶级思维
“营销狂人”小罐茶 杜国楹两大顶级思维
1.一定要有【参照物思维】
2.一定要有【终局思维】
趣讲大白话:大牛的思考就是不同
***********
杜国楹对茶行业思考
1.参照咖啡、酒的发展路径
2.中国茶工业化,品牌化是唯一壮大之路
3.龙头企业必须全品
没有参照物思维就没有位置感
在竞争环境中就会迷失
会自我陶醉
没有终局思维
就缺乏长远规划
中国企业的平均寿命3年左右
以20年的时间线来看
大部分企业烟消云散
大部分人从事的工作一换再换
连教育培训这样的“长久”的行业
一夜之间血流成河
【安志强趣讲信息科技】80期
掌握信息科技常识,未来竞争才不吃亏
世纪之问:做机器的奴隶?还是主人?
个人使命:让企业软件开发少走弯路
让信息科技赋能产业
培养信息科技二代
信息科技科普
一个资深软件从业者的【每日一记】

相关文章:

营销狂人杜国楹的两大顶级思维
“营销狂人”小罐茶 杜国楹两大顶级思维 1.一定要有【参照物思维】 2.一定要有【终局思维】 趣讲大白话:大牛的思考就是不同 *********** 杜国楹对茶行业思考 1.参照咖啡、酒的发展路径 2.中国茶工业化,品牌化是唯一壮大之路 3.龙头企业必须全品 没有参照物思维就没…...
)
面试题-前端开发JavaScript篇下(答案超详细)
文章目录 实现一个 once 函数,传入函数参数只执行一次将原生的 ajax 封装成 promisJS 监听对象属性的改变如何实现一个私有变量,用 getName 方法可以访问,不能直接访问==和===、以及 Object.is 的区别setTimeout、setInterval 和 requestAnimationFrame 之间的区别实现一个两…...
文字大小)
Android 9.0 修改Recovery字体图片的大小(正在清理)文字大小
1.概述 在9.0的系统产品定制化开发中,在系统中recovery功能也是非常重要的功能,所以说在进行recovery的时候,正在清理的 字体显示的有些小了,所以产品需求要求改大recovery的字体大小,所以这就需要在recovery页面看下字体大小的显示逻辑然后修改字体的显示大小,主要功能修…...
)
操作系统 五(文件系统)
一 文件定义:文件是指由创建者所定义的,具有文件名的一组相关元素的集合,可分为有结构文件和无结构文件两类。在有结构文件中,文件由若干个相关记录组成。而无结构文件则被看成一个字节流。文件在文件系统中是一个最大的数据单位&…...
)
华为OD机试 - 人数最多的站点(JS)
人数最多的站点 题目 公园园区提供小火车单向通行,从园区站点编号最小到最大, 通行如1~2~3~4~1万,然后供员工在各个办公园区穿梭, 通过对公司N个员工调研统计到每个员工的坐车区间,包含前后站点, 请设计一个程序计算出小火车在哪个园区站点时人数最多。 输入 输入的第…...
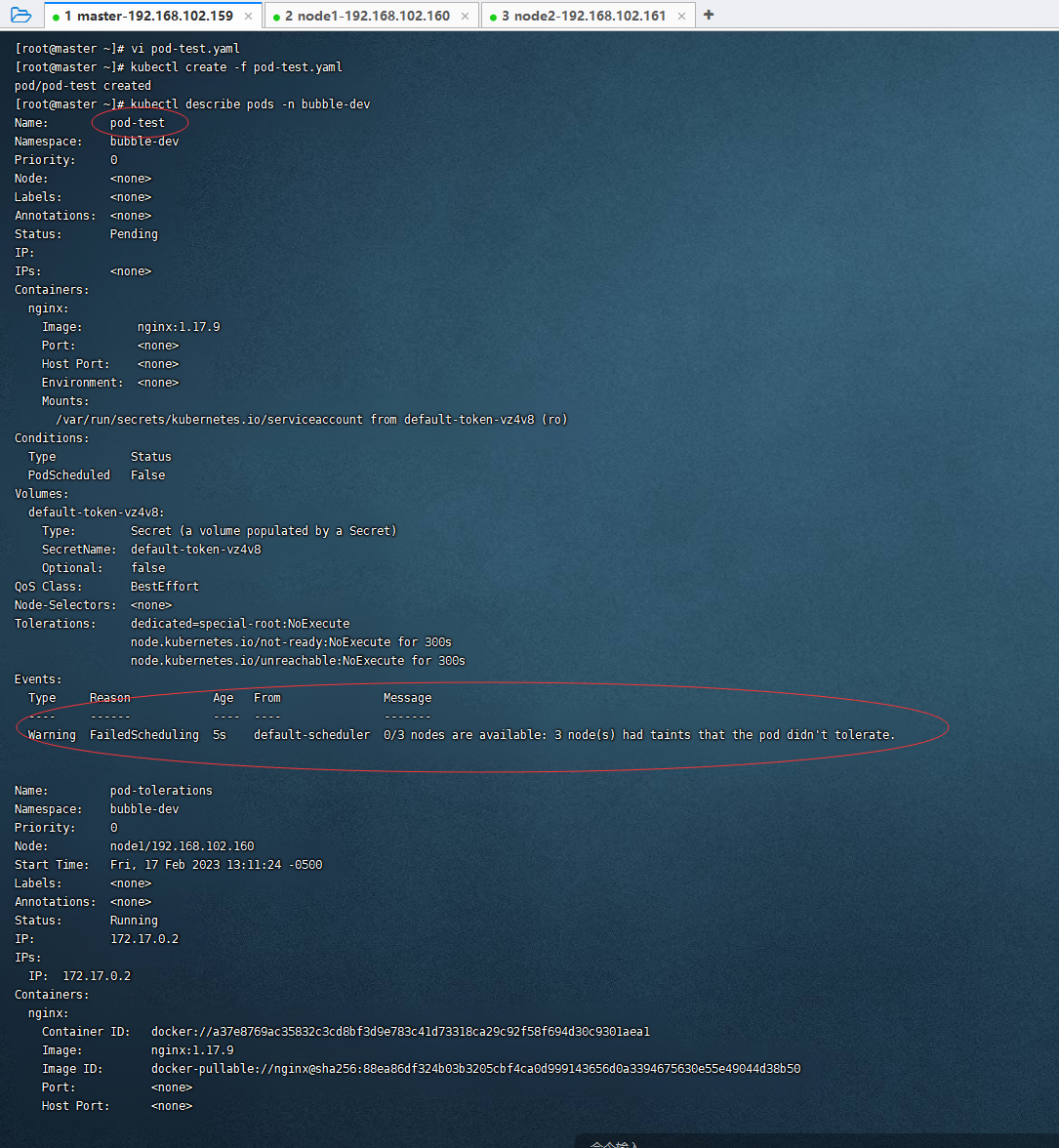
Mr. Cappuccino的第41杯咖啡——Kubernetes之Pod调度策略
Kubernetes之Pod调度策略Pod的4种调度策略定向调度nodeNamenodeSelector亲和性调度node亲和性硬限制软限制关系运算符pod亲和性pod反亲和性污点和容忍污点(taints)容忍(tolerations)默认情况下,Scheduler计算出一个Pod…...
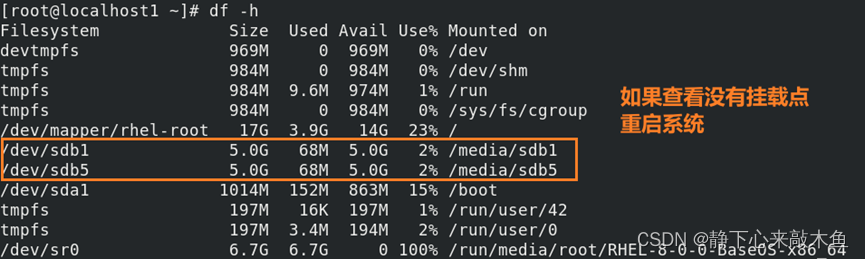
Linux 磁盘挂载
目录 Linux硬盘分区 硬盘设备的文件名 /dev/sd[a-z] 硬盘分区 识别硬盘的文件名 Linux文件系统 文件系统类型 Linux如何保存文件 VFS虚拟文件系统 磁盘挂载命令 lsblk 查看系统的磁盘使用情况 fdisk 硬盘分区 mkfs 格式化文件系统 mount 挂载命令 df 显示磁盘空间…...

命名冲突问题与命名空间
一、何为命名空间? 首先我们运行下面代码, #include <stdio.h> int rand 0; int main() {printf("%d", rand);return 0; } 我们会发现该代码能够正常运行,没有任何问题。 但是当我们再在上面代码的基础上包含stdlib.h头…...
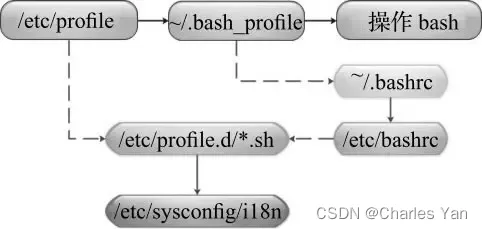
Kafka漏洞修复之CVE-2023-25194修复措施验证
Kafka漏洞修复之CVE-2023-25194修复措施验证前言风险分析解决方案AdoptOpenJDK Zookeeper Kafka多版本OpenJDK安装切换Zookeeper安装Kafka安装与使用其他Kafka消息发送流程Linux配置加载顺序参考链接前言 场景介绍 Kafka最近爆出高危漏洞CNNVD-202302-515,导致Apa…...

中后序遍历构建二叉树与应用I
目录 题目描述 思路分析 AC代码 题目描述 按中序遍历和后序遍历给出一棵二叉树,求这棵二叉树中叶子节点权值的最小值。 输入保证叶子节点的权值各不相同。 输入 测试数据有多组 对于每组测试数据,首先输入一个整数N (1 < N < 10000)&#x…...
)
随机退化模型--基础篇(1)
随机退化模型--基础篇(1) 1. 随机退化建模1.1 瞬间失效1.2 存在缓慢退化过程的失效2. 通俗解释2.1 包引入2.2 参数定义2.3 基于递归函数的更新2.4 结果可视化1. 随机退化建模 随机模型亦称“非确定的、概率的模型”,是按随机变量建立的模型。其特点是; 模型参数、模拟对象发…...
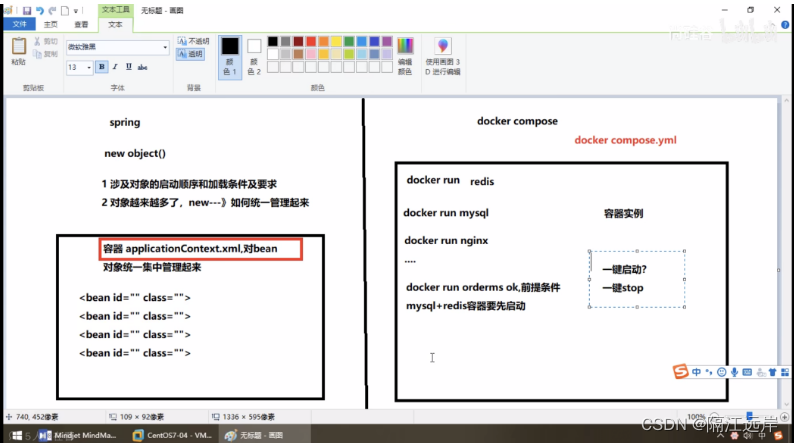
2023.2.15工作学习记录 git Docker compose容器编排
关于Git错误提交了target目录 是因为在ignore目录中没有加入biz这个工程 以后提交代码时一定要检查好自己提交的代码 首先把所有的全部取消 然后再根据自己要提交的内容一个个来勾选 Docker网络 container模式:新建的容器和已经存在的一个容器共享一个网络…...
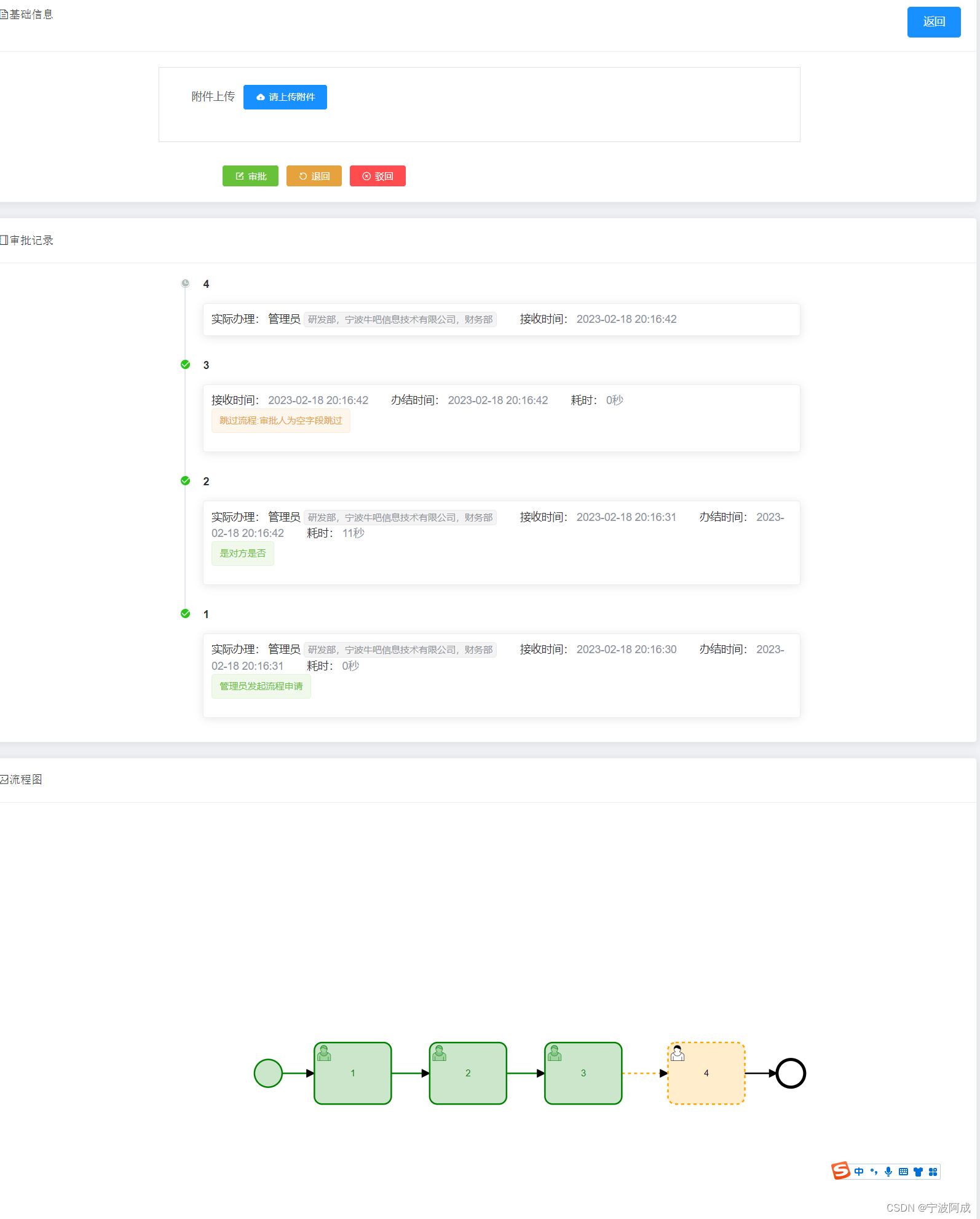
基于jeecgboot的flowable流程增加节点自动跳过功能
为了满足有时候需要在某个节点没有人员处理的时候需要自动跳过,所以增加了这个功能。 一、FlowComment意见里增加一个类型8,跳过流程 /** * 流程意见类型 * */ public enum FlowComment { /** * 说明 */ NORMAL("1", "…...
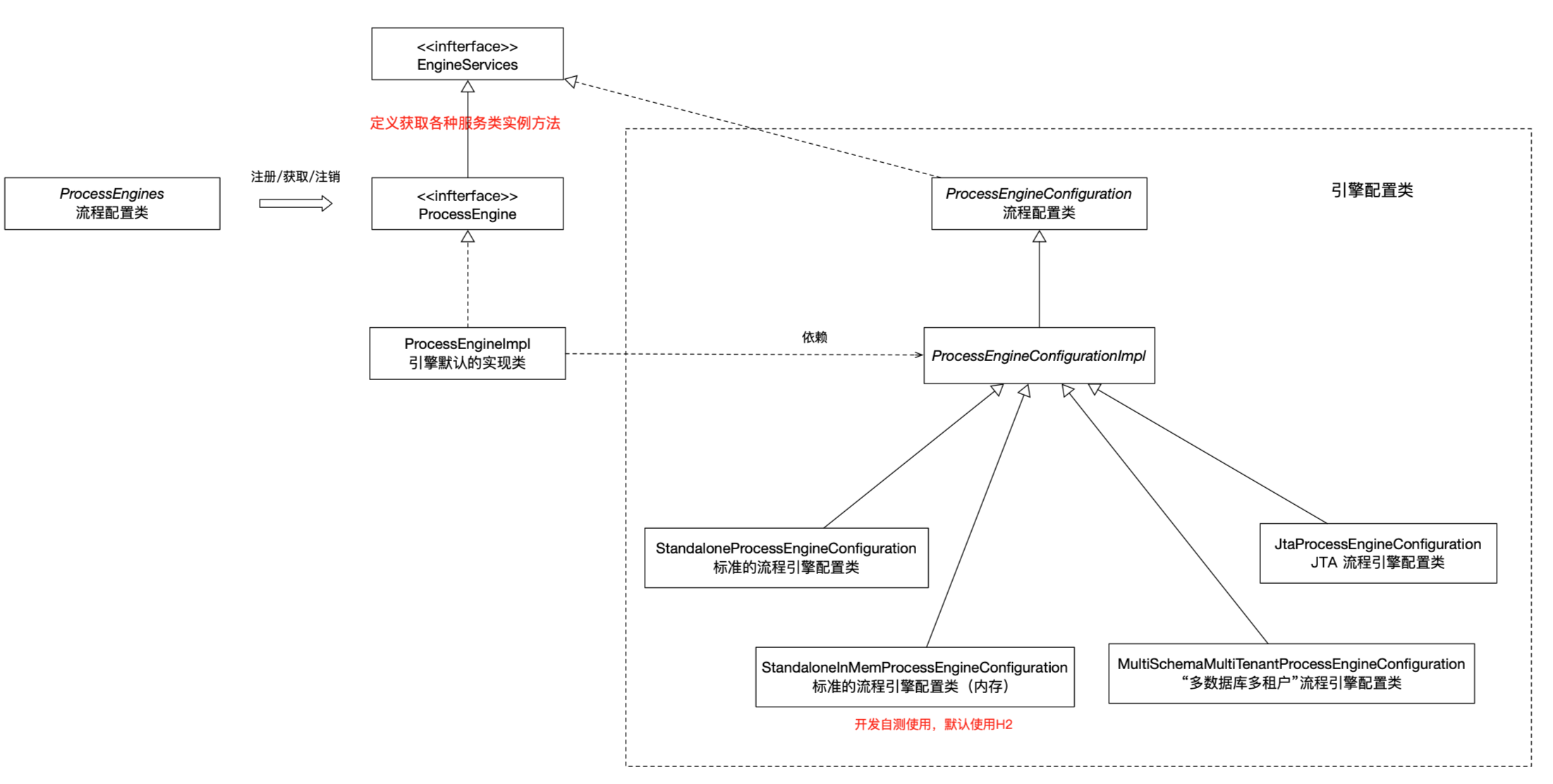
流程引擎之Activiti简介
背景Activiti 是一个开源架构的工作流引擎,基于 bpmn2.0 标准进行流程定义,其前身是 jBPM,Activiti 相对于 jBPM 更轻量,更易上手,且天然集成了 Spring。2010年 jBPM 创始人 Tom Baeyens 离开 JBoss,随之加…...

4.打包子应用 投票
接上回 最终得到这样的目录 mysite/manage.pymysite/__init__.pysettings.pyurls.pyasgi.pywsgi.pypolls/__init__.pyadmin.pyapps.pymigrations/__init__.py0001_initial.pymodels.pystatic/polls/images/background.gifstyle.csstemplates/polls/detail.htmlindex.htmlresult…...
 | 机试题算法思路 【2023】)
华为OD机试 - 服务依赖(JavaScript) | 机试题算法思路 【2023】
服务依赖 题目 在某系统中有众多服务,每个服务用字符串(只包含字母和数字,长度<=10)唯一标识,服务间可能有依赖关系,如A依赖B,则当B故障时导致A也故障。 传递具有依赖性,如A依赖B,B依赖C,当C故障时导致B故障,也导致A故障。给出所有依赖关系以及当前已知故障服务…...

目标检测综述(一份全的自制PPT): 涵盖各种模型简介对比,适合入门和了解目标检测现状
[TOC](目标检测综述(一份全的自制PPT): 涵盖各种模型简介对比,适合入门和了解目标检测现状) 注:本文仅供学习,未经同意勿转。分享的PPT请勿二次传播,或者用于其他商用途径。若使用本文PPT请注明来源,感谢配合 前言&…...

Vulnhub-DC-2实战靶场
Vulnhub-DC-2实战靶场 https://blog.csdn.net/ierciyuan/article/details/127560871 这次试试DC-2,目标是找到官方设置的5个flag。 一. 环境搭建 1. 准备工具 虚拟机Kali: 自备,我的kali的IP为192.168.3.129 靶场机: https…...

从输入URL到渲染的过程中到底发生了什么?
CDN缓存DNSTCP三次握手、四次挥手浏览器渲染过程输入URL到页面渲染过程的一些优化 下面我将“从输入URL到渲染的全过程”大概的描述出来,再对其过程加以解释,了解过程中可以做哪些优化。文章内容有点长,需要有足够的耐心看完哟!&…...

旋转屏幕导致 Fragment 中的 onConfigurationChanged 被调用两次
环境 IDE Android Studio Dolphin 2021.3.1; 项目配置 Android Gradle plugin version: 7.1.3 Gradle Version: 7.2 Gradle JDK: 11 Compile Sdk Version: 32 问题描述 项目使用的 Bottom Navigation Activity 基本结构,在调试程序时发现,…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...
