vb.net计算之.net core基础(4)-项目与程序结构（2）
相关文章：
-项目与程序结构（2）)
vb.net计算之.net core基础(4)-项目与程序结构（2）
目录 Namespace 语句Visual Basic 中的命名空间完全限定名命名空间可以定义什么全局关键字命名规范条件编译拆分和合并语句拆分成多行在同一行上放置多个语句为代码行添加标签注释串联成员访问运算符点运算符 `.`感叹号 `!`运算符Me 关键字MyMyBaseMyClassNamespace 语句 <…...
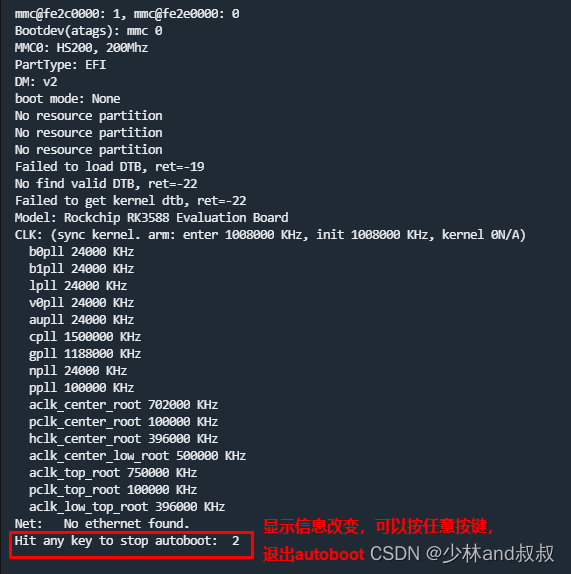
基于RK3588的嵌入式linux系统开发（五）——uboot优化修改（按任意按键停止autoboot）
我们通常情况下，芯片进入uboot后，会根据设置的bootdelay时间进行倒数计数。这时候在终端按任意键，即可退出autoboot，进入uboot的命令行模式。 官方提供的uboot源码中，为了防止调试串口干扰导致不能进入系统，…...
Lumerical---在FDTD和MODE工程中的PML边界条件
Lumerical---在FDTD和MODE工程中的PML边界条件 引言PML边界条件实现原理PML 类型PML 配置文件PML 配置文件选项Standard（标准）Stabilized（稳定性）Steep AngleCustom（陡角）对于不同的边界使用不同的配置FDE，varFDTD和FDTD SolverPML 参数阅读这篇前，推荐阅读边界条件综述…...
论文投稿指南——中文核心期刊推荐（社会学）
【前言】 🚀 想发论文怎么办？手把手教你论文如何投稿！那么，首先要搞懂投稿目标——论文期刊 🎄 在期刊论文的分布中，存在一种普遍现象：即对于某一特定的学科或专业来说，少数期刊所含…...
KVM-4、KVM 高级功能详解
1. 半虚拟化驱动 1.1 virtio 概述 KVM 是必须使用硬件虚拟化辅助技术（如 Intel VT-x 、AMD-V）的 Hypervisor，在CPU 运行效率方面有硬件支持，其效率是比较高的；在有 Intel EPT 特性支持的平台上，内存虚拟化的效率也较高。 QEMU/KVM 提供了全虚拟化环境，可以让客户机不经…...
【Linux】进程状态
文章目录1. 阻塞1. 举例2. 为什么要阻塞？3.操作系统层面上如何理解进程等待某种资源就绪呢？资源进程4. 总结2.挂起3.Linux进程状态1. R状态进程只要是R状态，就一定是在CPU运行吗？证明当前进程运行状态生成程序查看进程2. S休眠状态…...
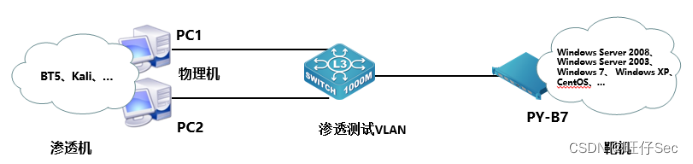
2023河南省第二届职业技能大赛郑州市选拔赛“网络安全”项目比赛样题任务书
2023河南省第二届职业技能大赛郑州市选拔赛“网络安全” 项目比赛样题任务书 一、竞赛时间 共计360分钟。 竞赛任务书内容 2023河南省第二届职业技能大赛郑州市选拔赛“网络安全” 项目比赛样题任务书 A模块基础设施设置/安全加固（200分） A-1&…...
pygame8 扫雷游戏
一、游戏规则： 1、点击方格，如果是地雷，游戏失败，找到所有地雷游戏胜利 2、如果方块上出现数字，则表示在其周围的八个方块中共有多少颗地雷 二、游戏主逻辑： 主要逻辑即调用run_game, 然后循环检测事件…...
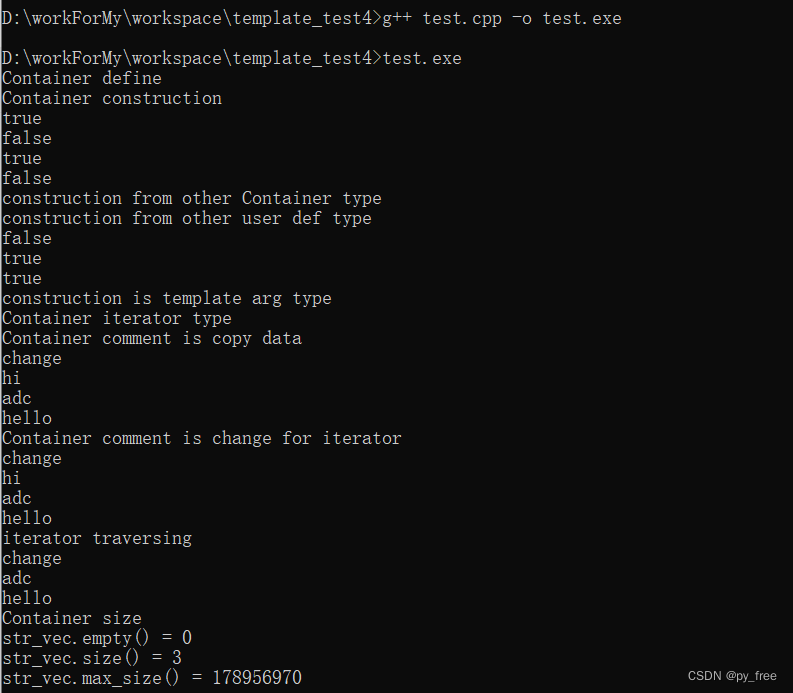
c/c++开发，无可避免的模板编程实践（篇四)
一、容器与模板 前文就说到，标准库基于模板编程，定义了许多容器类以及一系列泛型算法，使程序员可以更简洁、抽象和有效地编写程序。C标准库中有大量的标准容器，这些容器通常包含一组数据或对象的集合，几乎可以和任何类…...
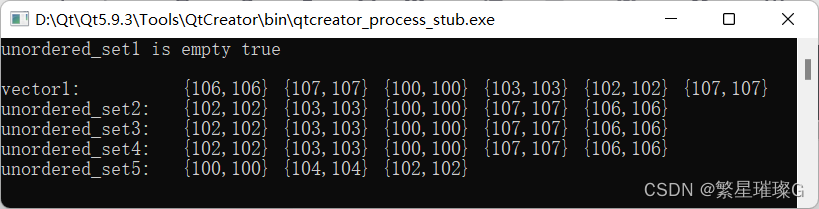
c++11 标准模板（STL）（std::unordered_set）（二）
定义于头文件 <unordered_set> template< class Key, class Hash std::hash<Key>, class KeyEqual std::equal_to<Key>, class Allocator std::allocator<Key> > class unordered_set;(1)(C11 起)namespace pmr { templ…...
GEE学习笔记 七十二：【GEE之Python版教程六】命令行简介
这篇开始就要讲解GEE相关的内容，首先聊一下命令行的内容，这个在官方文档中有详细的介绍，这里我简单说一下常用的几个命令，剩余的大家在使用过程中如果又需要可以随时查看相关官方文档的介绍。官方文档地址：https://dev…...
DDD单根 聚合根 实体 值对象
前言2004年Eric Evans 发表Domain-Driven Design –Tackling Complexity in the Heart of Software （领域驱动设计），简称Evans DDD。快二十年的时间，领域驱动设计在不断地发展，后微服务时代强调的东西，在国…...
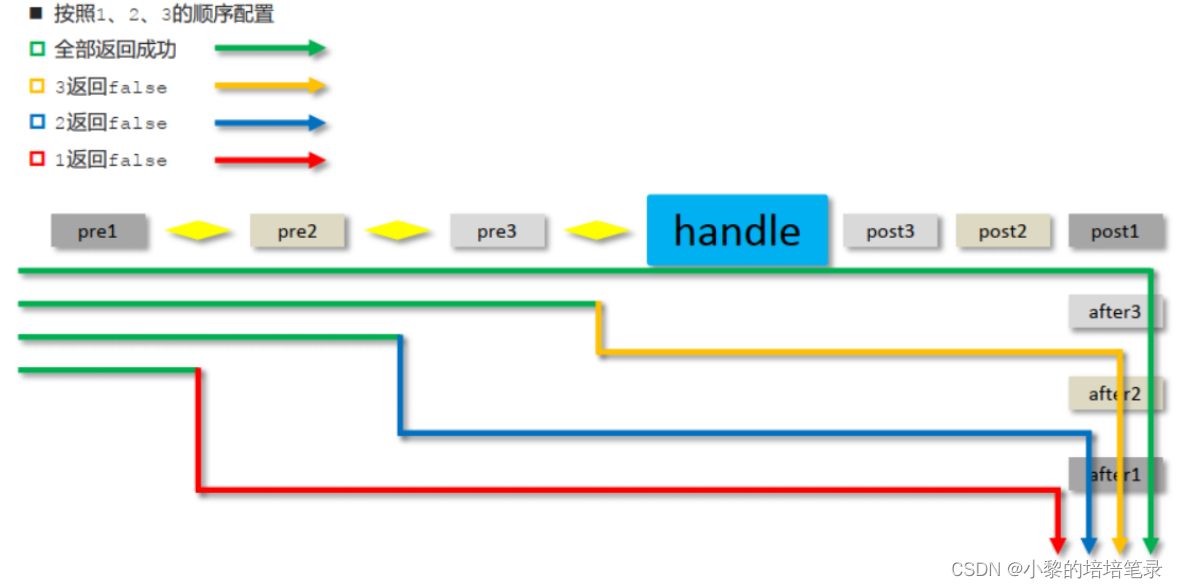
SpringMvc介绍。
目录 1、SpringMvc概述 1、基本介绍 2、工作流程 3、bean加载控制 二、请求 1、请求映射路径 2、请求方式 3、请求参数 4、请求参数（传递json数据） 5、日期类型参数传递 三、响应 四、REST风格 1、REST简介 2、RESTful入门案例 3、RESTfu…...
华为OD机试 - 最小传递延迟（JS）
最小传递延迟 题目 通讯网络中有N个网络节点 用1 ~ N进行标识 网络通过一个有向无环图进行表示 其中图的边的值，表示节点之间的消息传递延迟 现给定相连节点之间的延时列表times[i]={u,v,w} 其中u表示源节点，v表示目的节点，w表示u和v之间的消息传递延时 请计算给定源节点到…...
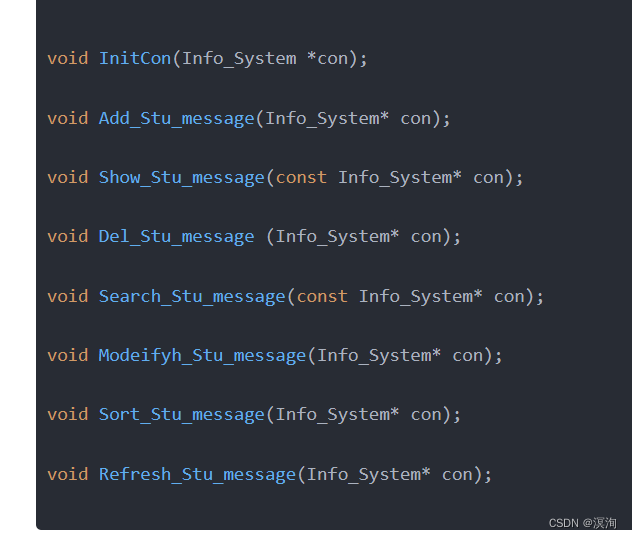
学生信息管理系统（通讯录）----------通俗易懂、附源码、C语言实现
绪论： 本篇文章使结构体章节后的习题，如果你对C语言有问题，或者结构体有什么问题不妨看看我之前所写的文章（章回体）,对于文件管理和内存分配问题我将在后面补上，对于这个学生信息管理系统我用了多种方法和…...
Python抽奖系统
#免费源码见文末公众号# 抽奖系统① def choujiang1():def write():with open(d:\\抽奖系统\\抽奖1.1.pickle,rb) as file:lst1pickle.load(file)namevar1.get()if name not in lst1 and name!录入成功！ and name!录入失败！ and name!:lst1.append(name)…...
真实景观渲染技巧【Three.js】
受到一些很棒的 three.js 演示、与 covid 相关的旅行禁令以及可能在 pinterest 上花太多时间看美丽的旅行照片的启发——我开始看看我是否可以使用 three.js 和r3f在浏览器中渲染一个令人信服的风景场景。 推荐：将 NSDT场景编辑器 加入你的3D开发工具链。 在过去一个…...
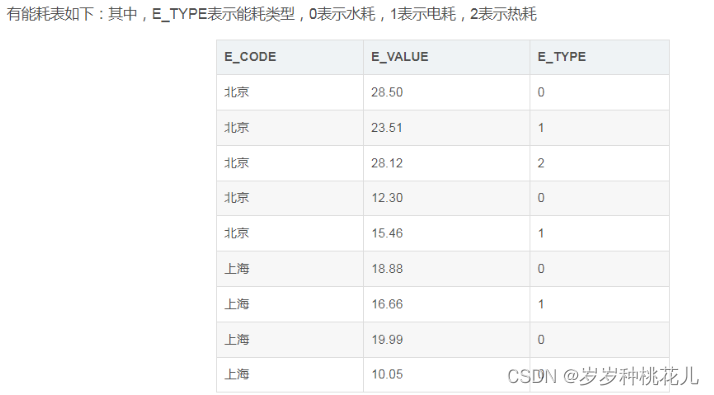
MySQL知识汇总：MySQL函数CASE WHEN用法详解
Case When的两种简单用法 用法一： CASE seasonWHEN Spring THEN 春天 WHEN Summer THEN 夏天 WHEN autumn THEN 秋天 else 冬天 end 用法二： CASE WHEN season Spring THEN 春天WHEN season Summer THEN 夏天WHEN season autumn THEN 秋天 els…...
Python学习-----模块1.0（模块的简介、定义与使用）
目录 前言： 1.什么是模块 2.模块的分类 （1）内置模块 （2）第三方模块 （3）自定义模块 3.模块的使用 4.自定义模块 5.模块和执行文件的判断 前言： 今天就开始讲Python中的模块篇…...
Linux进程学习【二】
✨个人主页： Yohifo 🎉所属专栏： Linux学习之旅 🎊每篇一句： 图片来源 🎃操作环境： CentOS 7.6 阿里云远程服务器 Perseverance is not a long race; it is many short races one after another…...
【Oracle APEX开发小技巧12】
有如下需求： 有一个问题反馈页面，要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据，方便管理员及时处理反馈。 我的方法：直接将逻辑写在SQL中，这样可以直接在页面展示 完整代码： SELECTSF.FE…...
【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat（I/O Statistics）是Linux系统下用于监视系统输入输出设备和CPU使…...
三体问题详解
从物理学角度，三体问题之所以不稳定，是因为三个天体在万有引力作用下相互作用，形成一个非线性耦合系统。我们可以从牛顿经典力学出发，列出具体的运动方程，并说明为何这个系统本质上是混沌的，无法得到一般解…...
WEB3全栈开发——面试专业技能点P2智能合约开发（Solidity）
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解，适合用作学习或写简历项目背景说明。 🧠 一、概念简介：Solidity 合约开发 Solidity 是一种专门为 以太坊（Ethereum）平台编写智能合约的高级编…...
高防服务器能够抵御哪些网络攻击呢？
高防服务器作为一种有着高度防御能力的服务器，可以帮助网站应对分布式拒绝服务攻击，有效识别和清理一些恶意的网络流量，为用户提供安全且稳定的网络环境，那么，高防服务器一般都可以抵御哪些网络攻击呢？下面…...
sipsak：SIP瑞士军刀！全参数详细教程！Kali Linux教程！
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求，并检查收到的响应。它以以下模式之一…...
Kafka入门-生产者
生产者 生产者发送流程： 延迟时间为0ms时，也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于：异步发送不需要等待结果，同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...
作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作：验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化：测试aof和aof持久化机制，确保数据在开启后正确恢复。 事务：检查事务的原子性和回滚机制。 发布订阅：确保消息正确传递。 2、性…...
认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持：CMake支持多种操作系统和编译器，使用同一份构建配置可以在不同的环境中使用 简化配置：通过CMakeLists.txt文件，用户可以定义项目结构、依赖项、编译选项等，无需手动编写复杂的构建脚本…...
k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率（或其他自定义指标）来调整这些对象的规模，从而帮助应用程序在负…...