时间复杂度(超详解+例题)
全文目录
- 引言
- 如何衡量一个算法的好坏
- 时间复杂度
- 时间复杂度的定义
- 时间复杂度的大O表示法
- 实例
- test1
- test2
- test3
- test4
- test5
- 总结
引言
如何衡量一个算法的好坏
我们在写算法的时候,对于实现同样的作用的不同算法,我们如何判断这个算法的好坏呢?
我们很容易的想到可以通过这个算法计算某用例的时间与所额外占用的空间来判断。
但是对于不同的计算机而言,数据读取与处理的速度与方式是可以有很大的差别的。所以单纯的根据算法某次运行的时间与空间来判断算法的效率高低是没有说服力的。
所以,我们使用时间复杂度与空间复杂度这两个标准来衡量算法的效率的高低。
在本篇文章中将介绍时间复杂度:
时间复杂度
时间复杂度的定义
在计算机科学中,时间复杂度是一个函数,它定量的描述了一个算法运行的时间。
前面提到,要实际的测出算法的运行时间是很麻烦的,有很多的不确定变量。而算法运行的时间往往与其中语句的执行次数成正比,所以算法中基本语句的执行次数为算法的时间复杂度。
时间复杂度的函数就是基本语句数量与相关变量之间的数学关系式。
例如:
int fun(int n)
{int i = 0;int j = 0;int count = 0;for (i = 0; i < n; i++){for (j = 0; j < n; j++){count++;}}for (i = 0; i < 2 * n; i++){count++;}int m = 10;while (m--){count++;}return count;
}
在这段代码中:
基本语句的数量与变量n与变量m有关,而m的值是恒定的。
所以我们可以得到这个函数的时间复杂度的数学表达式为 n^2+2*n+10。
虽然对于上面的代码而言,找到精确的数学表达式来表示时间复杂度是很容易的,但是对于一些比较复杂的算法而言,想要找到精确的函数是很困难的。所以我们使用大O表示法来表示时间复杂度的大概值。
时间复杂度的大O表示法
大O符号是用于描述函数渐进行为的数学符号。
我们在使用大O表示法表示时间复杂度时,去掉对结果影响不大的项即可。
大O表示法的转换规则如下:
1、用常数1表示算法中的所有加法常数;
2、在修改后的数学表达式中只保留最高项;
3、如果最高项存在且不是1,则去掉该最高项的系数。
得到的结果就是大O阶。
对于上面的fun函数:
我们已经得到了该数学表达式:n^2+2*n+10。
首先将常数10改为1;再将最高项保留,即n^2;这一项的系数为1。
所以大O阶就为 O(n^2)。
另外,某些算法在运行时对于不同的用例可能会有不同的情况。这时,我们采取最慢的情况来计算时间复杂度。
实例
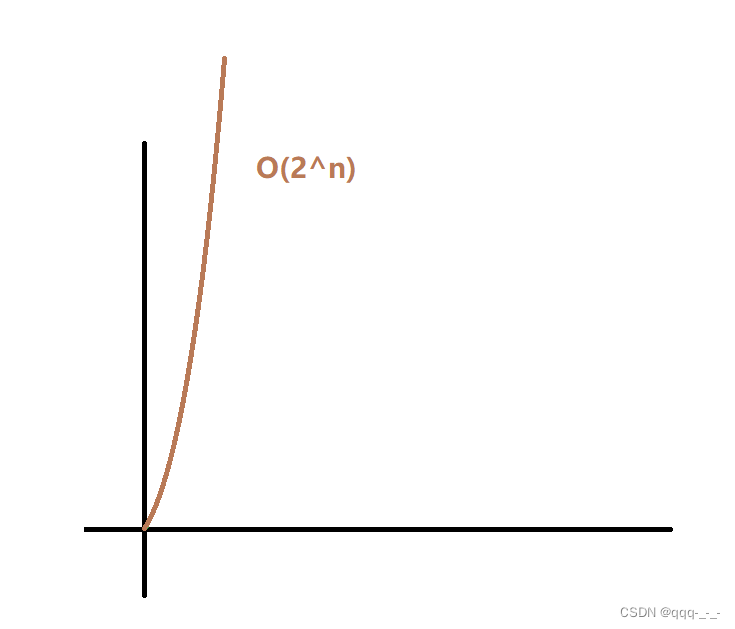
在实际用大O阶表示时间复杂度的时候,我们其实并不用通过精确的数学表达式来推出,只需要将该算法基本语句的量级表示出来即可。例如对数级(log n)、正比例级(n)、次方级(n^2)、指数级(2^n)等。这些量级都是可以用函数图像表示出来的:

例如上面的fun函数的量级就是n^2级的。
而确认量级的最佳途径往往是画图,接下来将通过几个栗子来说明:
test1
void test1(int N)
{int count = 0;for (int k = 0; k < 100; ++k){++count;}printf("%d\n", count);
}
在这段代码中:
显然,算法的基本操作的数量与k相关。
k的值从0开始随着算法的执行递增1,到100终止。所以我们可以画出它大概的图像:
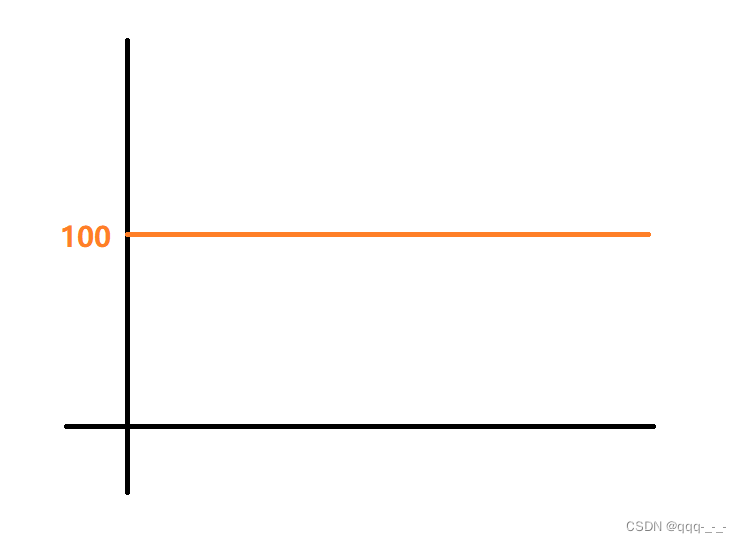
根据大O阶表示法,这个算法的时间复杂度就是O(1)。
test2
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
这个算法就是经典的冒泡排序算法。
对于冒泡排序算法,最好的情况是输入的数据已经是升序排列的,这种情况下只需要执行n次基本语句即可:
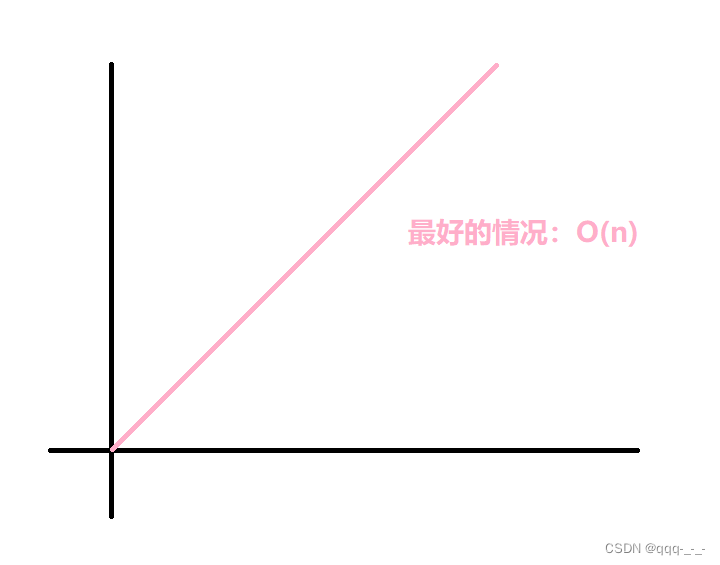
最坏的情况是完全降序的排列,此时就需要完全执行每一个基本语句,需要执行n^n次:
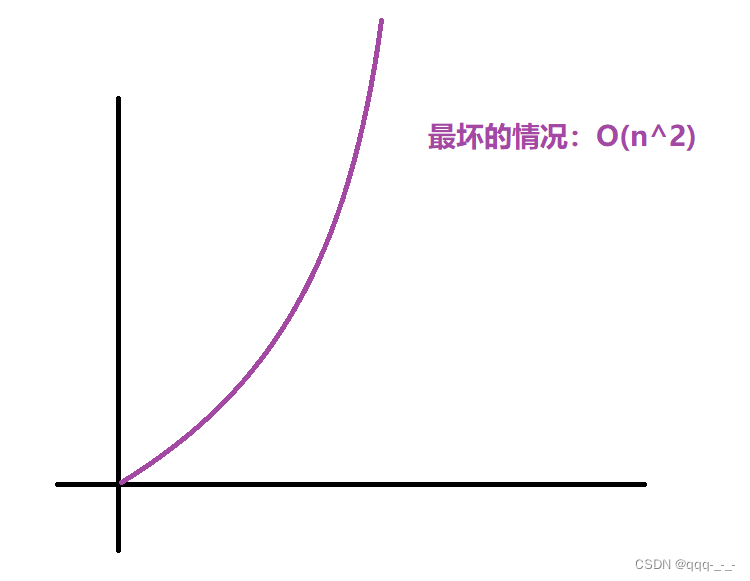
test3
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n - 1;// [begin, end]:begin和end是左闭右闭区间,因此有=号while (begin <= end){int mid = begin + ((end - begin) >> 1);if (a[mid] < x)begin = mid + 1;else if (a[mid] > x)end = mid - 1;elsereturn mid;}return -1;
}
这段代码就是经典的二分查找算法:
对于二分查找,是从n开始每次范围减少一半,知道剩余1个元素。
所以1乘以2的查找次数次方就是n,即需要执行log n次。我们就可以画出关系图:
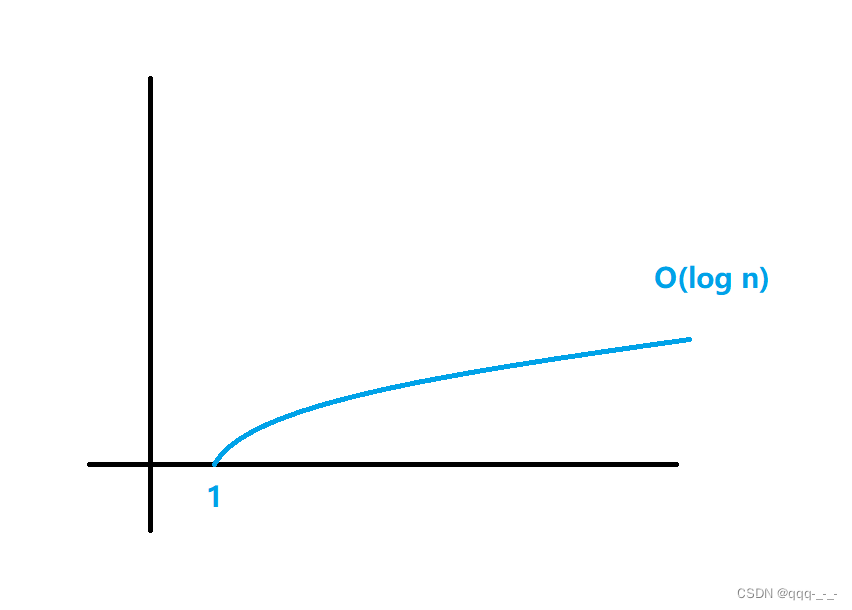
需要注意的是,由于书写较麻烦,对于log以2为底n的对数,所以可以用log n表示。
test4
long long Fac(size_t N)
{if (0 == N)return 1;return Fac(N - 1) * N;
}
这是一个函数递归的算法:
将N-1的值再传给函数本身,直到N为0时终止递归。
很明显,该算法每次递归N递减1,所以执行N次基本语句:

test5
long long Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
}
这是一个递归实现斐波那契数列的算法:
对于该算法,每次递归都会引起两次递归,即两次基本语句(N-1与N-2)。直到参数<3终止。
我们可以先画出这个算法的程序图:
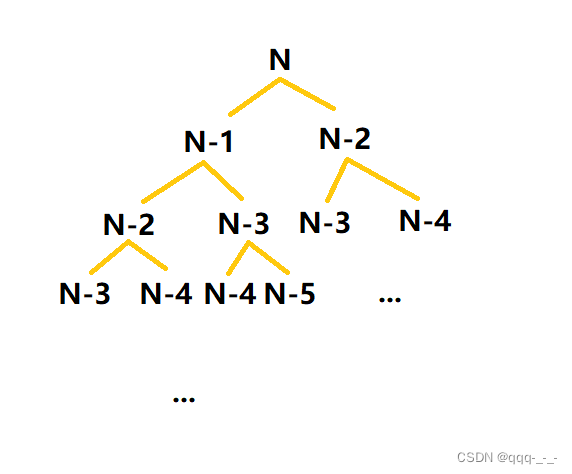
不难发现,基本语句的量级是指数增长的,所以该算法的时间复杂度为O(2^n):
总结
到此,关于时间复杂度的知识就介绍完了。
在下一篇文章中将详细介绍空间复杂度的相关知识,希望持续关注哦
如果大家认为我对某一部分没有介绍清楚或者某一部分出了问题,欢迎大家在评论区提出
如果本文对你有帮助,希望一键三连哦
希望与大家共同进步哦
相关文章:

时间复杂度(超详解+例题)
全文目录引言如何衡量一个算法的好坏时间复杂度时间复杂度的定义时间复杂度的大O表示法实例test1test2test3test4test5总结引言 如何衡量一个算法的好坏 我们在写算法的时候,对于实现同样的作用的不同算法,我们如何判断这个算法的好坏呢? …...

【Java面试总结】Maven篇
【Java面试总结】Maven篇1.Maven坐标是啥2.Maven常见的依赖范围有哪些?3.多模块如何聚合4.对于一个多模块项目,如果管理项目依赖的版本5.maven怎么解决版本冲突6.Maven常用命令有哪些?1.Maven坐标是啥 一般maven使用groupID,artifactId&…...

【每日一题Day123】LC1792最大平均通过率 | 堆
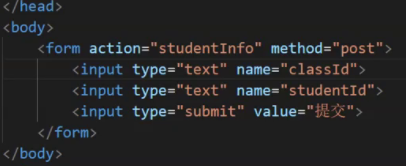
最大平均通过率【LC1792】 一所学校里有一些班级,每个班级里有一些学生,现在每个班都会进行一场期末考试。给你一个二维数组 classes ,其中 classes[i] [passi, totali] ,表示你提前知道了第 i 个班级总共有 totali 个学生&#…...

[安装之5] Mac pro更换大内存固态硬盘实践教程
近由于mac电脑内存吃紧,安装大的软件,是不是要提示一下内存不够,内心非常的不爽。作为一款A1502版的mac,128G固态硬盘通常被称为“乞丐版”。提前做好准备工作后,我周末花了一天的时间搞定这件事,为了能够帮…...

04 Python变量的声明与使用
基本上,在所有的计算机编程语言中,都会用到变量,变量将数据存储在计算机内存中。 变量是指存储数据的内存地址,通过变量名,我们可以找到这个变量名对应的内容。 命名变量时不允许使用数字、特殊字符、连字符开头。 变量可以有一个短名称(如 x、y、z),但强烈建议使用更具…...

LeetCode 2418. 按身高排序
给你一个字符串数组 names ,和一个由 互不相同 的正整数组成的数组 heights 。两个数组的长度均为 n 。 对于每个下标 i,names[i] 和 heights[i] 表示第 i 个人的名字和身高。 请按身高 降序 顺序返回对应的名字数组 names 。 示例 1: 输…...
一文了解Hotspot虚拟机下JAVA对象从创建到回收的生命周期
Java虚拟机是Java的核心和基础,他是Java编译器和操作系统平台之间处理器,能实现跨平台运行Java程序。本文主要讲解的是虚拟机如何管理对象,即Java对象在JVM虚拟机中被创建到回收的流程 Java对象从创建到回收的生命周期对象创建流程1.类加载检…...

【Java基础】Java对象创建的几种方式
先上关键内容,所用到的代码请参考文末示例代码。一、使用new关键字创建对象这是一种最常用的创建对象的方式。Student student1 new Student();二、使用Class的newInstance()方法创建对象需要有一个无参构造方法,这个newInstance()方法调用无参的构造函…...

社保缴费满15年就可以不缴了?6个很多人最关心的问题权威解答来了
一、社保缴费满15年就可以不缴了? 上海市政府新闻办公室2022年在微信号发文表示,社会保险是由国家通过立法强制建立的社会保障制度,用人单位和劳动者都必须依法参加社会保险。即使职工与用人单位商议签订了不参加社保的所谓“协议”…...
关于HDFS
目录 一、HDFS概述 二、HDFS架构与工作机制 三、HDFS的Shell操作 四、Hdfs的API操作 一、HDFS概述 HDFS:Hadoop Distributed File System;一种分布式文件管理系统,通过目录树定位文件。使用场景:一次写入,多次读出…...

C++入门:类 对象
C 在 C 语言的基础上增加了面向对象编程,C 支持面向对象程序设计。类是 C 的核心特性,通常被称为用户定义的类型。类用于指定对象的形式,它包含了数据表示法和用于处理数据的方法。类中的数据和方法称为类的成员。函数在一个类中被称为类的成…...
Python生日系统
#免费源码见文末公众号# 录入生日 def write():keyvar1.get()valuevar2.get()with open(d:\\生日系统.pickle,rb) as file:dictspickle.load(file)dicts[key]valuewith open(d:\\生日系统.pickle,wb) as file:pickle.dump(dicts,file)file.close() 查询生日 def read():namev…...

< CSDN周赛解析:第 28 期 >
CSDN周赛解析:第 27 期👉 第一题: 小Q的鲜榨柠檬汁> 题目解析> 解决方案👉 第二题: 三而竭> 解析> 解决方案> 拓展知识👉 第三题: 隧道逃生> 解析> 解决方案👉…...

【题外话】如何拯救小米11Pro这款工业垃圾
1 背景媳妇用小米11Pro手机,某日不慎摔落,幸好屏幕未碎,然而WiFi却怎样都无法打开,初以为是系统死机,几天依旧故障无法使用。现在的手机没有WiFi功能,就无法刷抖音、看视频,就是鸡肋了。后抽空去…...

Python中有哪些常用操作?这20个你都会吗
Python 是一个解释型语言,可读性与易用性让它越来越热门。 正如 Python 之禅中所述: 优美胜于丑陋,明了胜于晦涩。 在你的日常编码中,以下技巧可以给你带来意想不到的收获。 1、字符串反转 下面的代码片段,使用 P…...
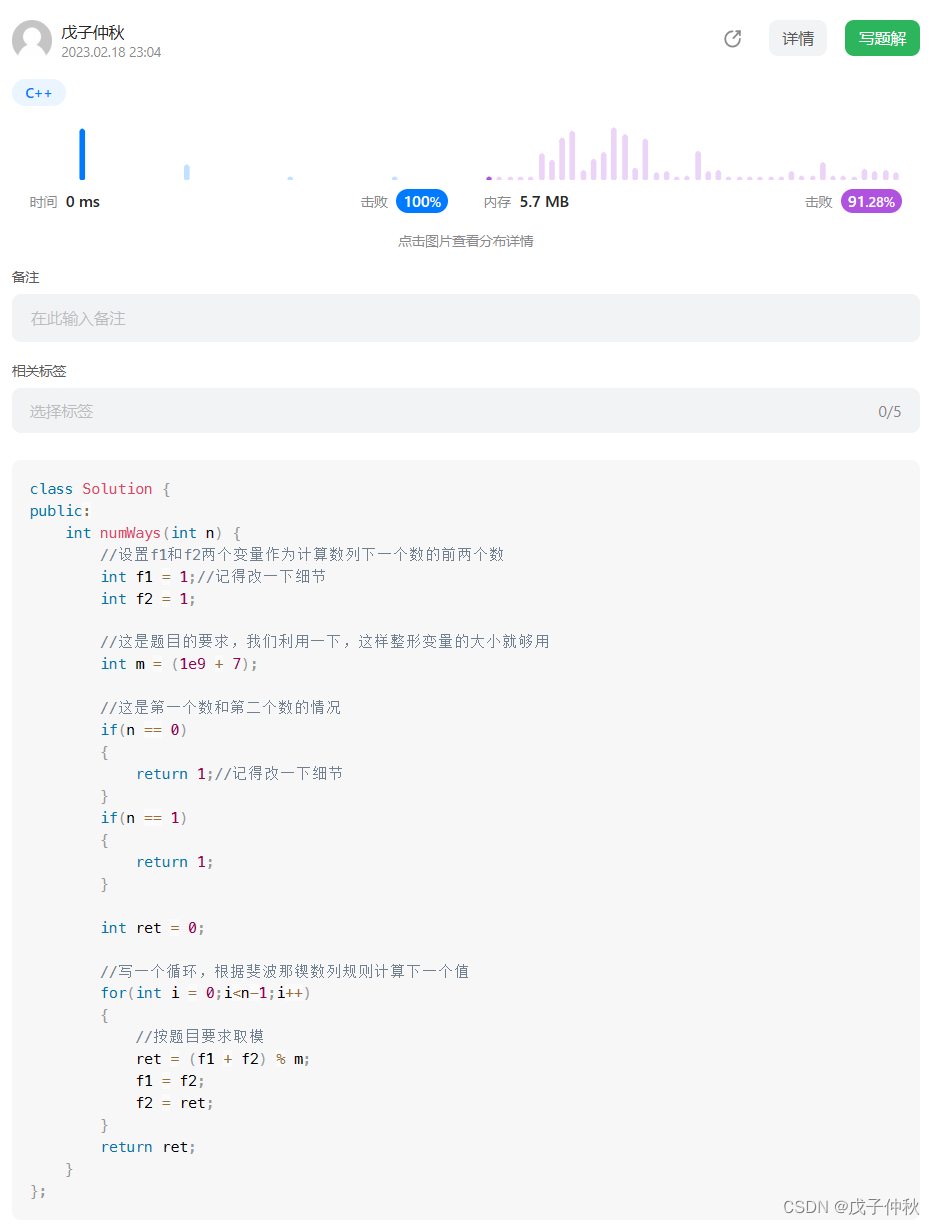
【LeetCode】剑指 Offer(4)
目录 写在前面: 题目:剑指 Offer 10- I. 斐波那契数列 - 力扣(Leetcode) 题目的接口: 解题思路: 代码: 过啦!!! 题目:剑指 Offer 10- II. …...
庄懂的TA笔记(十二)<>
庄懂的TA笔记(十二)<>一、作业展示,答疑:1、作业:2、答疑:二、作业示范,分析:1、文档分析:2、资源分析:3、资源优化:4、光…...
)
学分绩点(2023寒假每日一题 5)
北京大学对本科生的成绩施行平均学分绩点制(GPA)。 既将学生的实际考分根据不同的学科的不同学分按一定的公式进行计算。 公式如下: 实际成绩 绩点 90——100 4.0 85——89 3.7 82——84 3.3 78——81 3.0 75…...
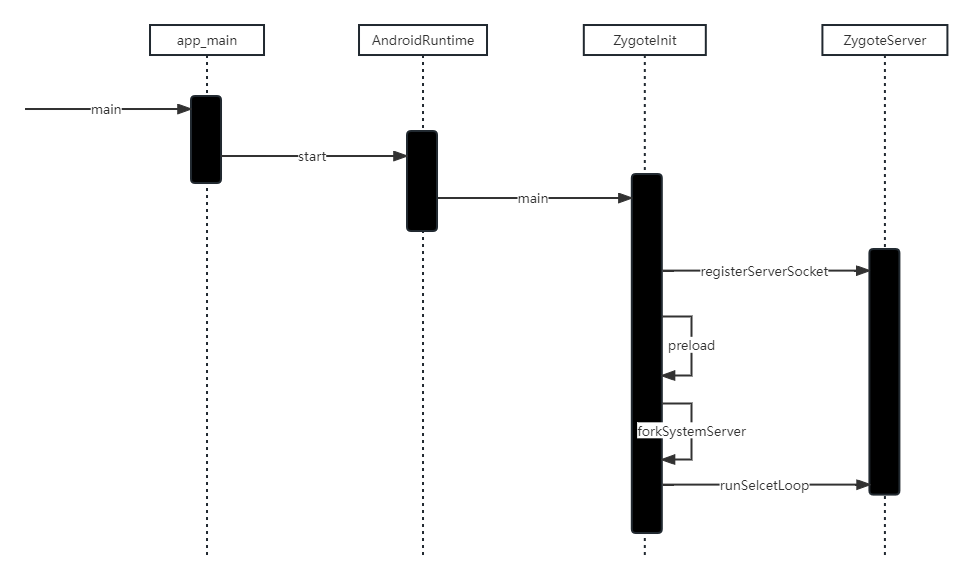
Framework学习之旅:Zygote进程
概述 在Android系统中,DVM(Dalvik 虚拟机和ART、应用程序进程以及运行系统的关键服务SystemServer进程都是由Zygote进程来创建的。通过fork(复制进程)的形式来创建应用程进程和SystemServer进程,由于Zygote进程在启动时会创建DVM…...
HTTP基础知识
关键字:一问一答用于和服务器交互什么是HTTPHTTP是个应用层协议,是HTTP客户端和HTTP服务器之间的交互数据格式。所以这里有个实例:在浏览网页的时候,浏览器会向服务器发送一个HTTP请求,告诉服务器我想访问什么..然后服…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...
