图解LeetCode——剑指 Offer 10- II. 青蛙跳台阶问题
一、题目
一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
二、示例
2.1> 示例 1:
【输入】n = 2
【输出】2
2.2> 示例 2:
【输入】n = 7
【输出】21
2.3> 示例 3:
【输入】n = 0
【输出】1
提示:
0<= n <=100
三、解题思路
根据题目描述,青蛙只能跳1级台阶或者跳2级台阶,那么我们可以针对这个条件,演示一下不同台阶青蛙的跳法。比如:
- 对于1阶台阶来说,小青蛙只有1种跳法,就是向上跳1级;
- 对于2阶台阶来说,小青蛙有2种跳法,分别是:向上跳1级然后再跳1级 & 直接向上跳2级;
- 对于3阶台阶来说,小青蛙有3种跳法,分别是:执行3次1级跳 & 直接向上跳2级再跳1级 & 先跳1级然后直接向上跳2级;
- 对于4阶台阶来说,小青蛙有5种跳法,分别是:执行4次1级跳 & 2次1级跳再直接跳2级 & 直接跳2级再执行2次1级跳 & 1级跳再直接跳2级再执行1次1级跳 & 执行2次2极跳;
- ……
针对上面描述,我们来看下面图示,会更好理解一些:
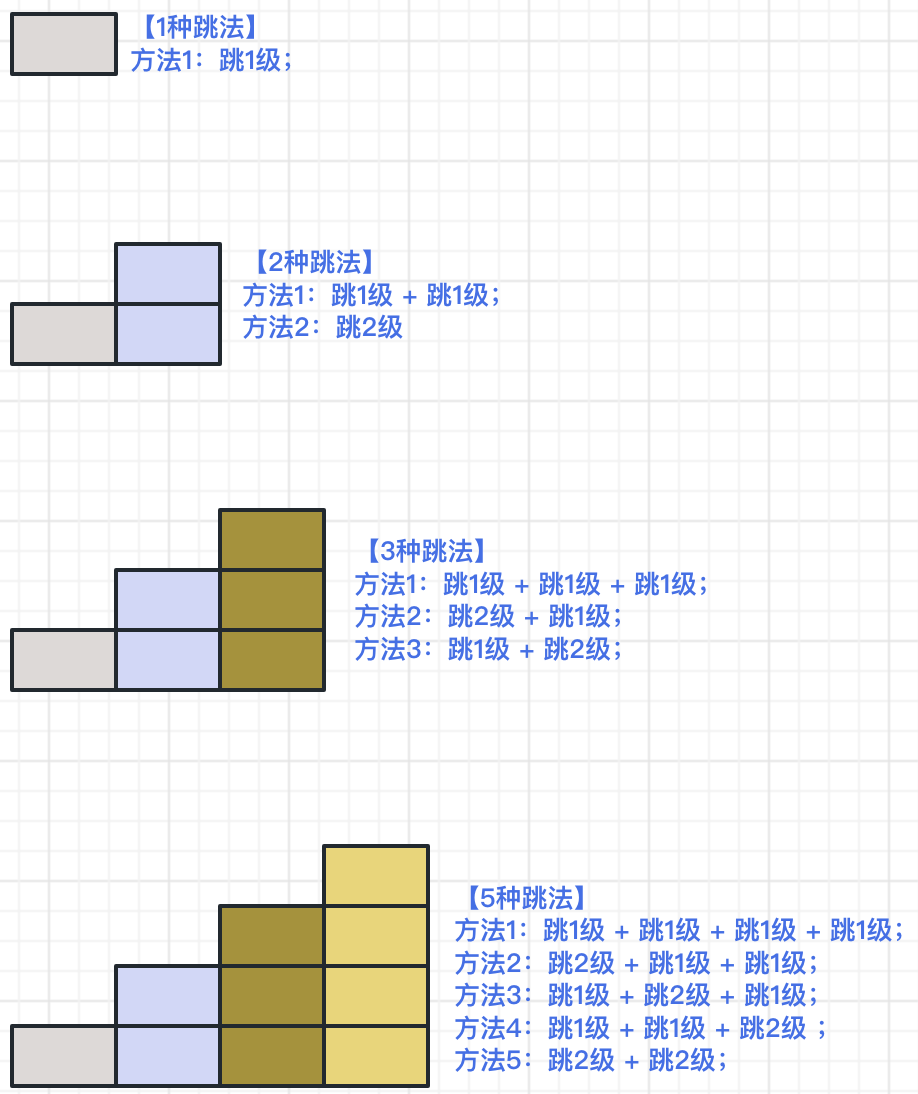
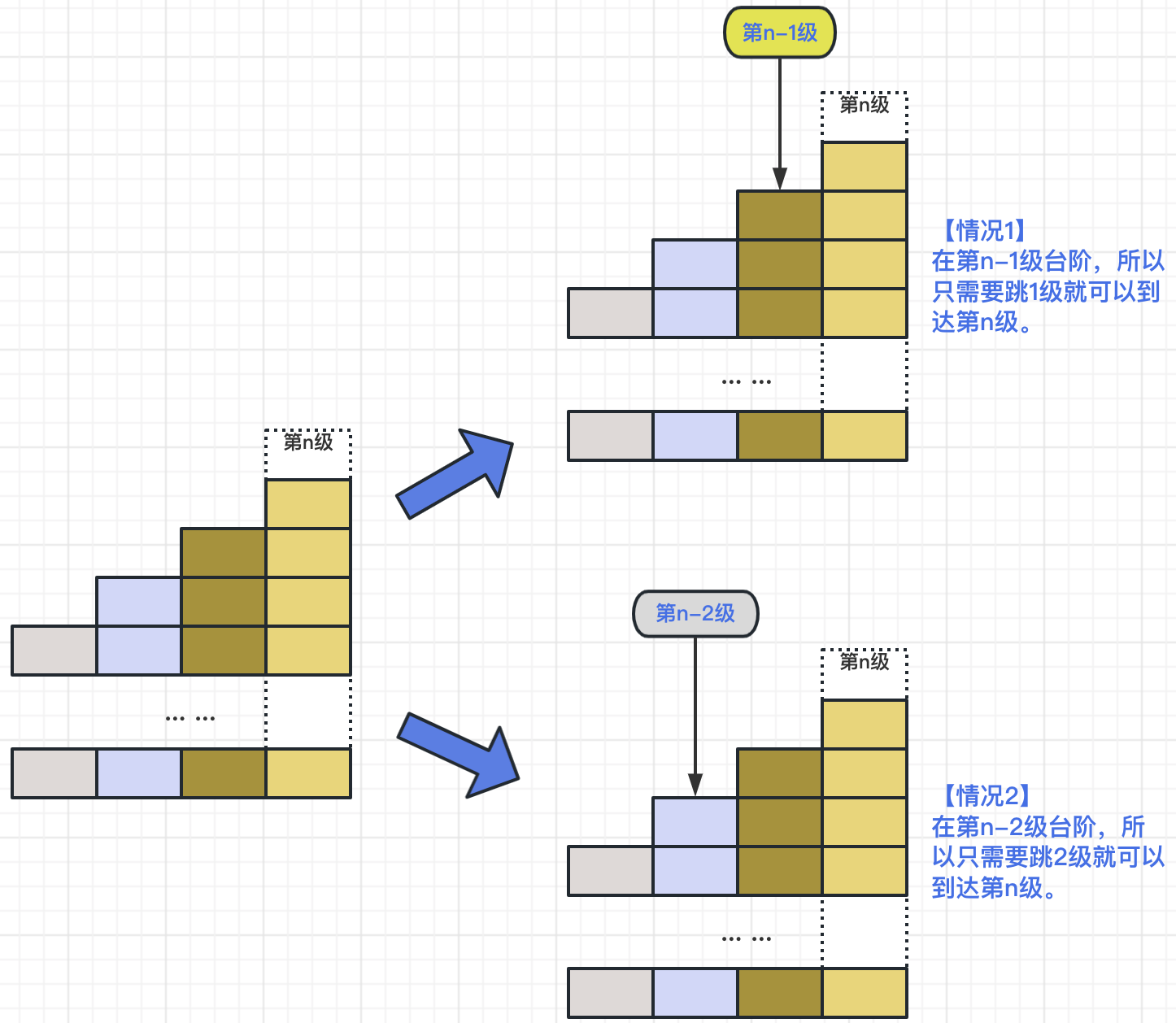
从上面的示例中,我们可以看到从1阶到4阶的跳法分别是:1种、2种、3种、5种……,是不是似曾相识呢?是的,就是斐波那契数列!那为什么会是这样的规律呢?下面我们以第n级台阶来看,对于它来说,往前一步其实只有两种情况:
【情况1】在第
n-1级处,那么只需要向上跳1步即可。
【情况2】在第n-2级处,那么只需要向上跳2步即可。
既然是这样,我们以f(n)表示到达第n级阶梯的跳法,那么可以推理出 f(n) = f(n-1) + f(n-2) , 所以,我们根据推导出的公式关系,就可以解出——青蛙跳上一个 n 级的台阶总共有多少种跳法了。
四、代码实现
class Solution {public int numWays(int n) {int a = 1, b = a, c = b, mod = (int)1e9 + 7;for (int i = 2; i <= n; i++, a = b, b = c) c = (a + b) % mod;return c;}
}
今天的文章内容就这些了:
写作不易,笔者几个小时甚至数天完成的一篇文章,只愿换来您几秒钟的 点赞 & 分享 。
更多技术干货,欢迎大家关注公众号“爪哇缪斯” ~ \(^o^)/ ~ 「干货分享,每天更新」
相关文章:

图解LeetCode——剑指 Offer 10- II. 青蛙跳台阶问题
一、题目 一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。 答案需要取模 1e97(1000000007),如计算初始结果为:1000000008,请返回 1。 二、示例 2.1>…...

【Linux】用户分类+权限管理+umask+粘滞位说明
目录 1.用户分类 su指令 2.认识Linux权限 2.1 文件访问者的分类 2.2 文件类型和访问权限 a. 文件类型 file指令 b. 访问权限 2.3 文件权值的表示方法 a. 字母表示法 b. 八进制表示法 3.如何修改文件访问者的权限及相关指令 1. chmod指令 2. chown指令 3. chgrp指…...
【干货】如何打造HR无法拒绝的简历?测试开发大牛带手把手你写简历!
通过率90%,优秀的软件测试简历长什么样? 也许口才好的人会觉得简历不重要,能说就行了,那是因为你没有体会过石沉大海的感觉! 很多人觉得疑惑,为什么我投了那么多简历,都没有接到面试通知&…...
nodejs学习-4:nodejs连接mongodb和相关操作
1. express生成器生成express模板 前提需要首先下载好:express-generator,命令如下(全局安装) npm install -g express-generator生成模板命令如下: express 项目名称 --viewejs // --view 参数表示前端界面使用的引擎,这里使用…...

【博客629】Linux DNS解析原理与配置
Linux DNS解析原理与配置 1、DNS缓存 作用: 程序客户端、下游的 DNS 服务器每次查询 DNS 成功之后,通常会将该 DNS 记录缓存一段时间,避免频繁发出查询请求的耗时。 Linux下的DNS缓存: Linux 系统默认不会在本地建立 DNS 缓存…...

【CSP】202212-2 训练计划
题目 问题背景 西西艾弗岛荒野求生大赛还有 天开幕! 问题描述 为了在大赛中取得好成绩,顿顿准备在 天时间内完成“短跑”、“高中物理”以及“核裂变技术”等总共 项科目的加强训练。其中第 项( )科目编号为 ,也可简…...
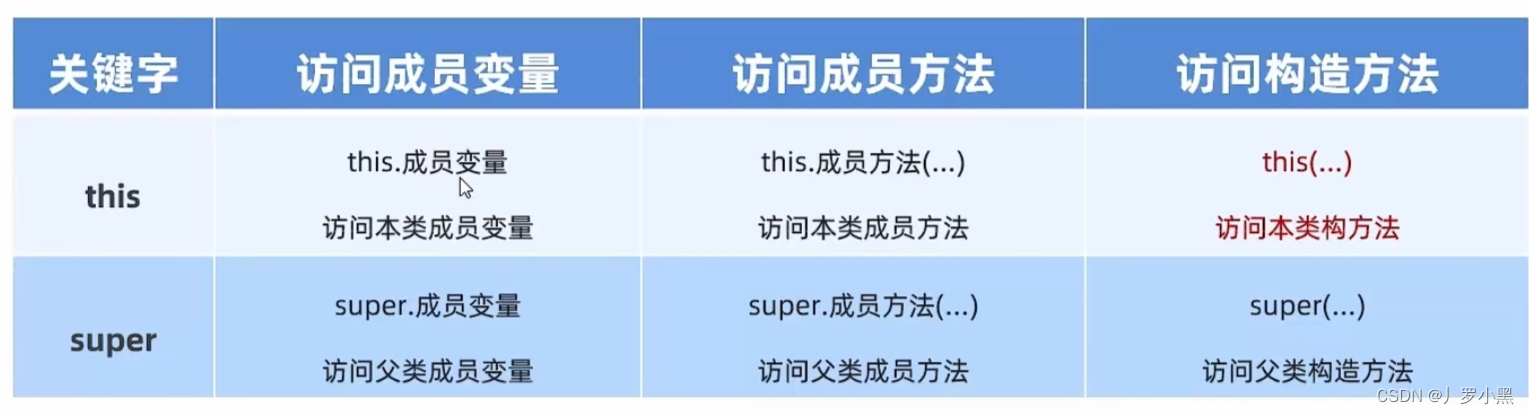
java基础学习 day42(继承中构造方法的访问特点,this、super的使用总结)
继承中,构造方法的访问特点 父类的构造方法不会被子类继承,但可以通过super()调用父类的构造方法,且只能在子类调用,在测试类中是不能手动单写构造方法的。子类中所有的构造方法默认先调用父类的无参构造,再执行自己构…...

生物医药多组学与生物信息方法介绍
基因组学告诉你可能发生什么,转录组学和蛋白组学告诉你即将发生什么,而代谢组学告诉你正在发生什么 1、多组学与生信方法 生物医学技术的组学包括基因组学、转录组学、蛋白质组学、代谢组学和表观基因组学等。这些组学研究领域通过大量数据的高通量技术…...
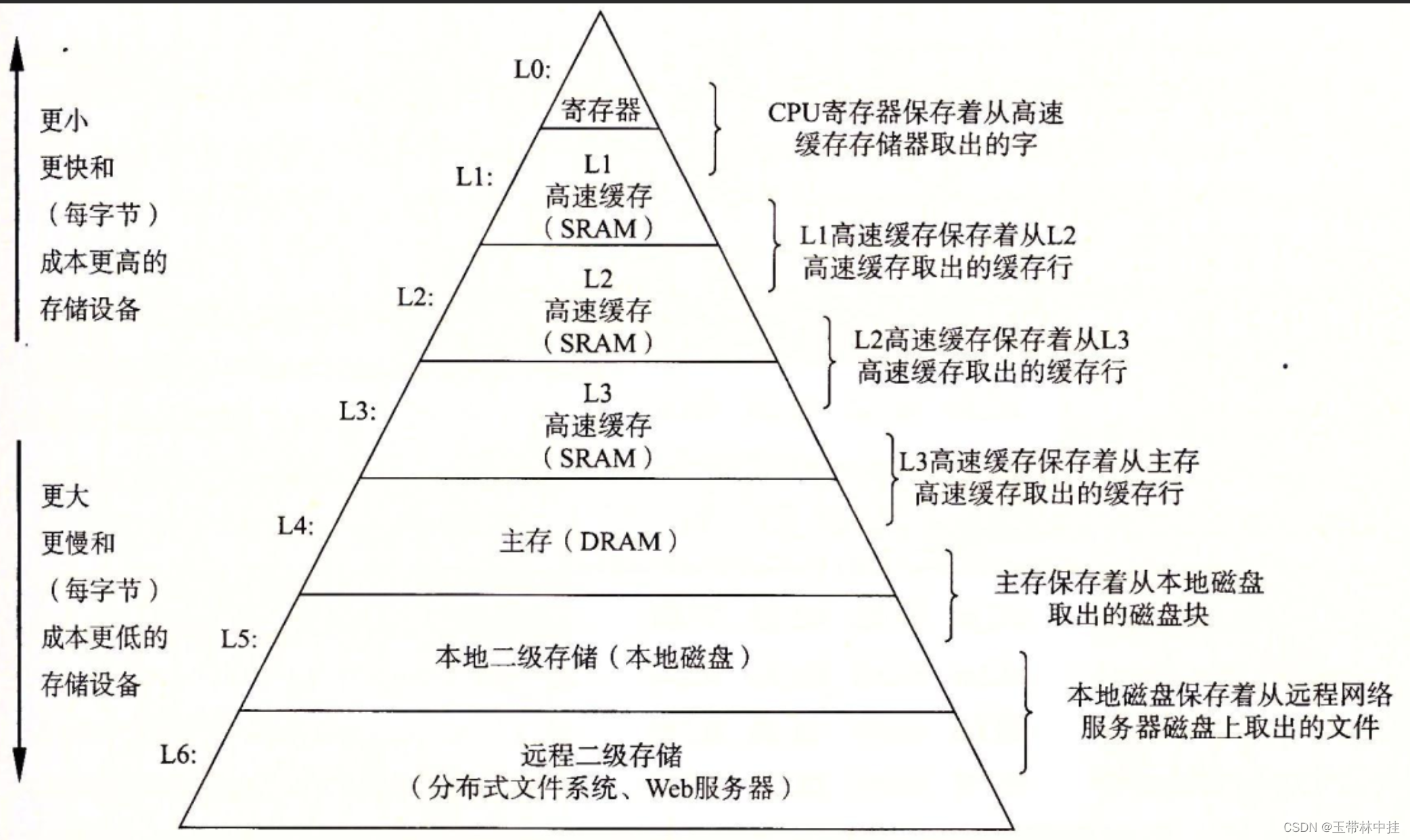
【进阶篇】线程的硬件基础
文章目录高速缓存缓存一致性协议写缓冲区和无效化队列高速缓存 简介 高速缓存是主内存与处理器之间的硬件,其容量小于主存,但存取速率远高于主存。因此处理器在执行读写操作时,可直接和高速缓存交互,提高响应速度。 我们常见的变…...

关于 ISP Tuning的学习,分享几点看法
关于学习,分享几点看法,欢迎讨论 。1、分阶段性的,阶梯式学习。2、带目的性的,任务式学习。3、有总结性的,输出式学习。如上3条,可以依次循环去执行,下面我以 ISP Tuning 的学习为例,…...

RocketMQ源码阅读
没有用过rocketmq,但是一直对RocketMQ的实现很感兴趣,本次阅读源码基于5.0.0 一、 nameserver 通过源码阅读发现,它的作用主要是当作一个注册中心,注册broker、topic等信息,维护topic以及broker队列的路由信息&#…...
重磅 | 小O软件新品【鲸鱼地图】发布
千呼万唤始出来.......,小O系列软件又添新品【鲸鱼地图】!!! 2023年新年伊始,小O就投入到新品研发工作中,秉承“发现地理价值”理念,为用户提供更加好用、易用的地图软件产品,经过春…...

软考高级信息系统项目管理师系列之二十五:项目合同管理
软考高级信息系统项目管理师系列之二十五:项目合同管理 一、项目合同管理内容整理一、合同管理基本概念1.项目合同管理定义2.合同的分类3.合同类型选择4.合同内容二、合同管理过程1.合同管理过程的内容2.合同签订和履行管理3.合同变更和档案管理4.合同违约索赔管理项目合同管理…...

测试开发之Django实战示例 第十三章 上线
在上一章,为其他程序与我们的Web应用交互创建了RESTful API。本章将学习如何创建生产环境让我们的网站正式上线,主要内容有:配置生产环境创建自定义中间件实现自定义管理命令1创建生产环境现在该将Django项目正式部署到生产环境中了。我们将按…...
)
python实战应用讲解-【语法基础篇】Python中的数值类型(附示例代码)
目录 前言 数值类型 十六进制、八进制和二进制 Python 数值类型转换 数值和表达式 前言...
Git常用命令以及如何在IDEA中使用Git
前言Git是一个分布式版本控制工具,主要用于管理开发过程中的源代码文件(Java类、xml文件、html页面等)。Git在管理文件过程中会记录日志,方便回退到历史版本;Git存在分支的概念,一个项目可以有多个分支&…...
音乐播放器-- 以及数据库数据存储
运行环境 : java1.8 数据库以及代码编写工具 : sqlserver -- mysql 也可以 工具 eclipse 编码gbk窗体 : Swing使用了jaudiotagger 进行了音乐处理 图片展示 ----- 空闲时间 做出来玩的项目 部分功能还没有完善 完善了的功能 音乐 /// 主页 &a…...
[JAVA安全]Spring Messaging之CVE-2018-1270
漏洞简介 Spring 框架中通过spring-messaging 模块来实现 STOMP (Simple Text-Orientated Messaging Protocol),STOMP是一种封装 WebSocket的简单消息协议。攻击者可以通过建立WebSocket连接并发送一条消息造成远程代码执行, spring-messagin…...
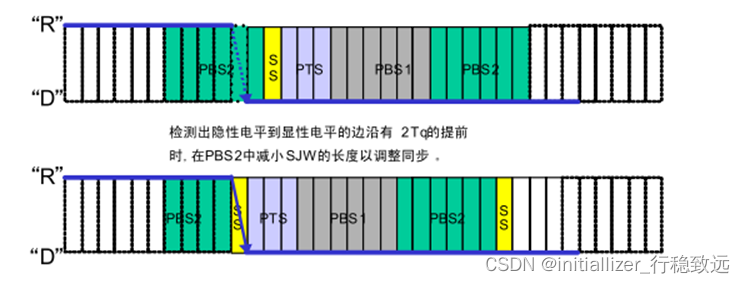
CAN通信笔记-位时间、Tq及采样点同步
本文框架1.前言2. 位时间2.1 位时间定义2.2 位时间计算3. Tq3.1 Tq的计算3.1.1 举个例子3.2 位时间与Tq的换算4. 采样点同步4.1 硬同步4.2 重同步4.2.1 延长PBS1的重同步4.2.2 缩短PBS2的重同步1.前言 本篇记录些关于CAN的一些学习笔记,说实话CAN协议发展的已经非常…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

