leetcode 1792. 最大平均通过率
一所学校里有一些班级,每个班级里有一些学生,现在每个班都会进行一场期末考试。给你一个二维数组 classes ,其中 classes[i] = [passi, totali] ,表示你提前知道了第 i 个班级总共有 totali 个学生,其中只有 passi 个学生可以通过考试。
给你一个整数 extraStudents ,表示额外有 extraStudents 个聪明的学生,他们 一定 能通过任何班级的期末考。你需要给这 extraStudents 个学生每人都安排一个班级,使得 所有 班级的 平均 通过率 最大 。
一个班级的 通过率 等于这个班级通过考试的学生人数除以这个班级的总人数。平均通过率 是所有班级的通过率之和除以班级数目。
请你返回在安排这 extraStudents 个学生去对应班级后的 最大 平均通过率。与标准答案误差范围在 10-5 以内的结果都会视为正确结果。
示例 1:
输入:classes = [[1,2],[3,5],[2,2]], extraStudents = 2
输出:0.78333
解释:你可以将额外的两个学生都安排到第一个班级,平均通过率为 (3/4 + 3/5 + 2/2) / 3 = 0.78333 。
示例 2:
输入:classes = [[2,4],[3,9],[4,5],[2,10]], extraStudents = 4
输出:0.53485
提示:
1 <= classes.length <= 105
classes[i].length == 2
1 <= passi <= totali <= 105
1 <= extraStudents <= 105
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/maximum-average-pass-ratio
* @param {number[][]} classes* @param {number} extraStudents* @return {number}*/
var maxAverageRatio = function (classes, extraStudents) {const heap = new PriorityQueue({compare: (a, b) => {let val1 = (b[1] + 1) * b[1] * (a[1] - a[0]);let val2 = (a[1] + 1) * a[1] * (b[1] - b[0]);if (val1 == val2) {return 0;}return val1 < val2 ? 1 : -1}})classes.forEach(([pass, total]) => {heap.enqueue([pass, total])})while (extraStudents--) {const [pass, total] = heap.dequeue()heap.enqueue([pass + 1, total + 1])}let ans = 0while (heap.front()) {const [pass, total] = heap.dequeue()ans += Number(pass / total)}return ans / classes.length
};
使用指南可以看这个:
@datastructures-js/priority-queue作者:hai-jia-er-shan-de-luo-ri
链接:https://leetcode.cn/problems/maximum-average-pass-ratio/solution/javascriptyou-xian-dui-lie-ke-yi-shi-yon-1wkq/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。相关文章:

leetcode 1792. 最大平均通过率
一所学校里有一些班级,每个班级里有一些学生,现在每个班都会进行一场期末考试。给你一个二维数组 classes ,其中 classes[i] [passi, totali] ,表示你提前知道了第 i 个班级总共有 totali 个学生,其中只有 passi 个学…...

15-基础加强-2-xml(约束)枚举注解
文章目录1.xml1.1概述【理解】(不用看)1.2标签的规则【应用】1.3语法规则【应用】1.4xml解析【应用】1.5DTD约束【理解】1.5.1 引入DTD约束的三种方法1.5.2 DTD语法(会阅读,然后根据约束来写)1.6 schema约束【理解】1.6.1 编写schema约束1.6.…...
)
13:高级篇 - CTK 事件管理机制(signal/slot)
作者: 一去、二三里 个人微信号: iwaleon 微信公众号: 高效程序员 在《12:高级篇 - CTK 事件管理机制(sendEvent/postEvent)》一文中,我们介绍了如何进行插件间通信 - sendEvent()/postEvent() + ctkEventHandler。然而,除了这种方式之外,EventAdmin 还提供了另一种方…...
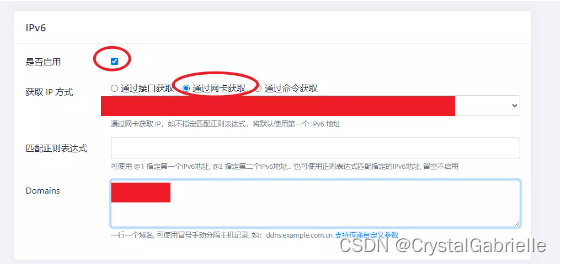
群晖-第1章-IPV6的DDNS
群晖-第1章-IPV6的DDNS 方案:腾讯云群晖DS920 本文参考群晖ipv6 DDNS-go教程-牧野狂歌,感谢原作者的分享。 这篇文章只记录了我需要的部分,其他的可以查看原文,原文还记录了更多的内容,可能帮到你。 一、购买域名 …...
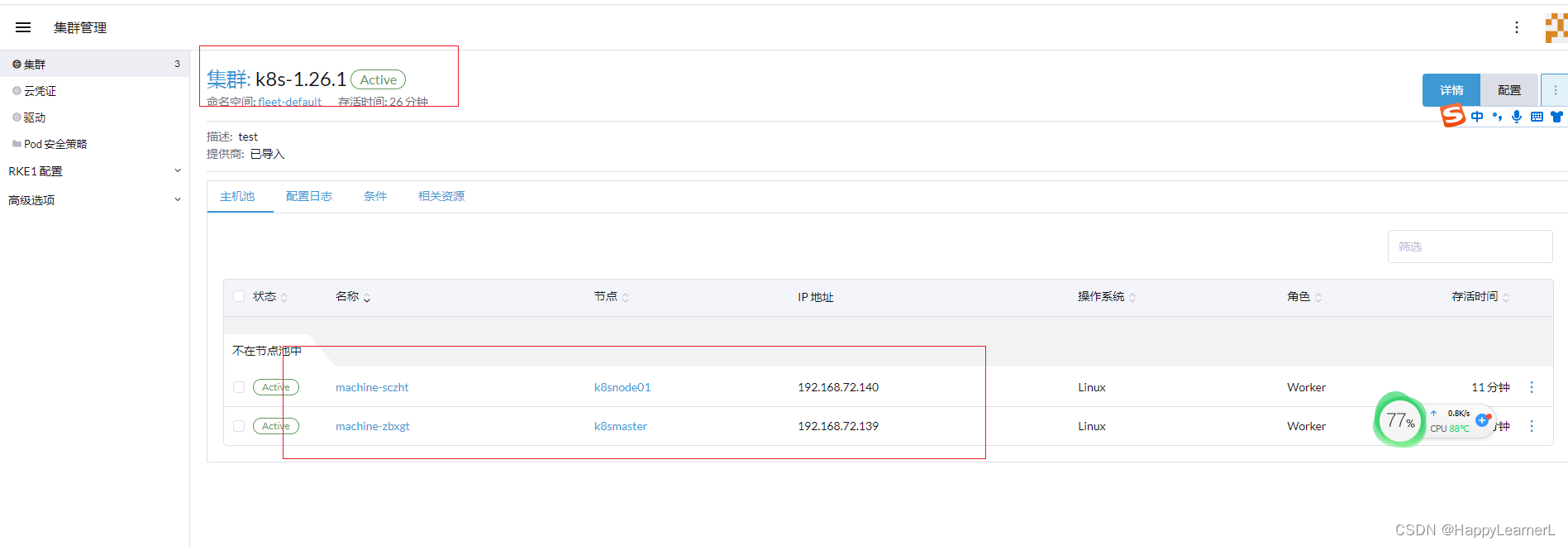
centos7系统-kubeadm安装k8s集群(v1.26版本)亲测有效,解决各种坑可供参考
文章目录硬件要求可省略的步骤配置虚拟机ip设置阿里镜像源各服务器初始化配置配置主节点的主机名称配置从节点的主机名称配置各节点的Host文件关闭各节点的防火墙关闭selinux永久禁用各节点的交换分区同步各节点的时间将桥接的IPv4流量传递到iptables的链(三台都执行…...
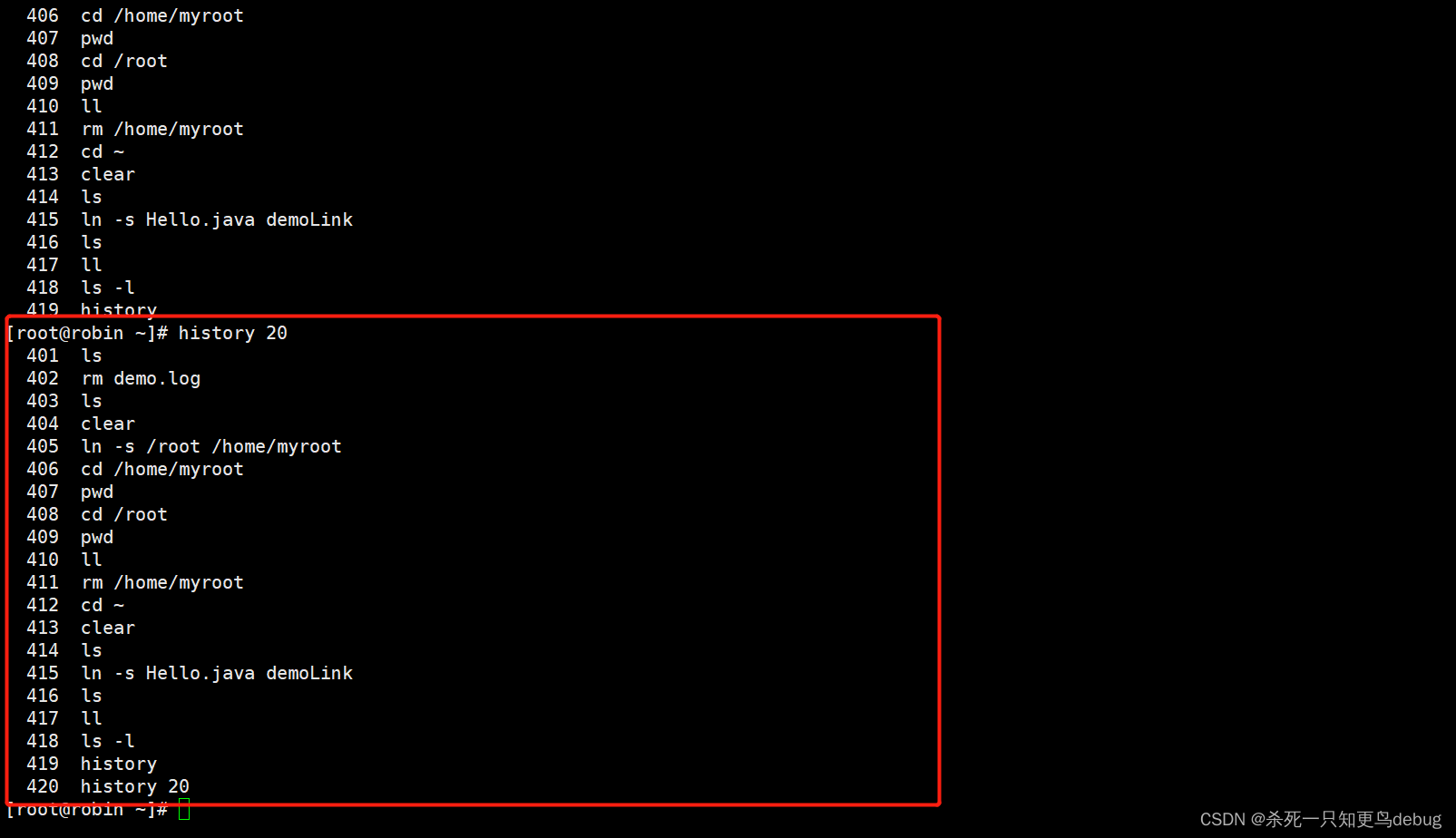
帮助指令 man ,help及文档常用管理指令
帮助指令 man,help 1. man 当我们想要了解某个命令如何使用,及选项的含义是什么以及配置文件的帮助信息时,可以使用 man [命令或配置文件],这样便可以获得到帮助提示信息了。 语法格式:man [命令或者配置文件] 比如…...
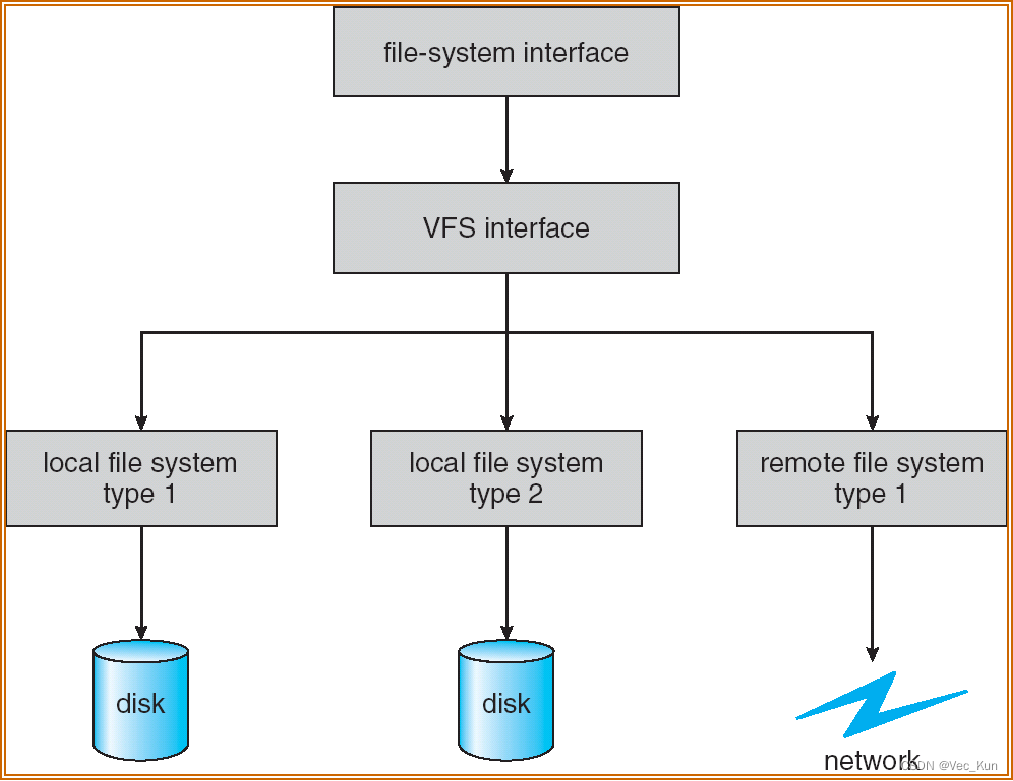
电子科技大学操作系统期末复习笔记(五):文件管理
目录 前言 文件管理:基础 基本概念 文件 文件系统 文件系统的实现模型 文件的组成 文件名 文件分类 文件结构 逻辑结构 物理结构 练习题 文件管理:目录 文件控制块FCB FCB:File Control Block FCB信息 目录 基本概念 目…...
SpringBoot+ActiveMQ-发布订阅模式(生产端)
SpringBootActiveMQ-发布订阅模式(生产端)Topic 主题* 消息消费者(订阅方式)消费该消息* 消费生产者将发布到topic中,同时有多个消息消费者(订阅)消费该消息* 这种方式和点对点方式不同…...
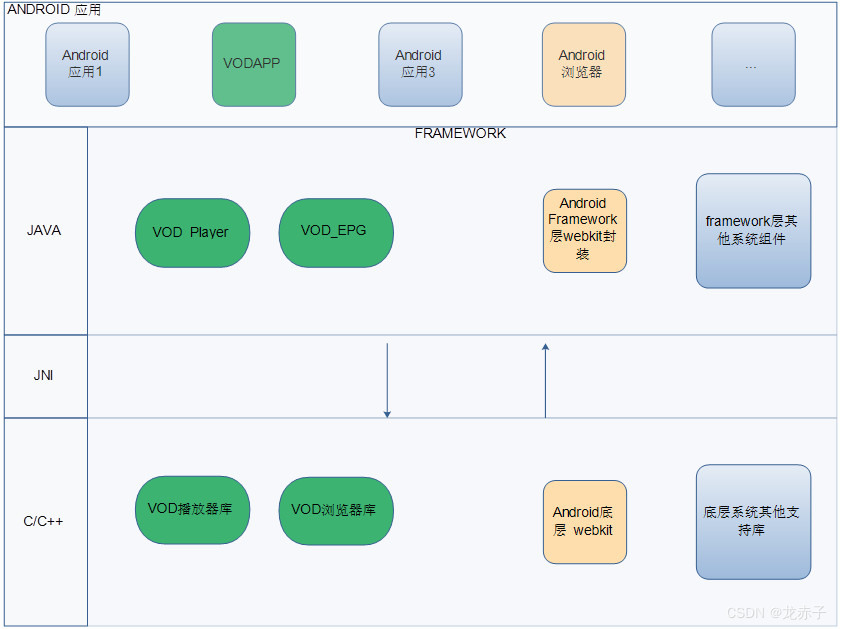
Android实例仿真之三
目录 四 Android架构探究 五 大骨架仿真 六 Android实例分析思路拓展 四 Android架构探究 首先,Android系统所带来的好处,就在于它本身代码的开放性,这提供了一个学习、借鉴的平台。这对分析仿真而言,本身就是一大利好…...
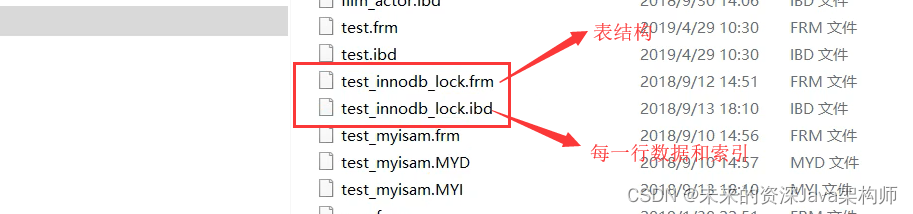
关于MySQL的limit优化
1、前提 提示:只适用于InnoDB引擎 2、InnoDB存储特点 它把索引和数据放在了一个文件中,就是聚集索引。这与MyISAM引擎是不一样的。 3、SQL示例 -- 给cve字段建立索引 select * from cnnvd where cveCVE-2022-24808 limit 300000,10;由于M…...

Java-Stream流基本使用
collection.stream将会破坏原有的数据结构,可以通过collect方法收集,可以用Collectors提供的构造器,add等方法构造形成新的数据结构。 HashSet<List<Integer>> rs new HashSet<>(); rs.stream().toList();Collection集合转…...

Liunx(狂神课堂笔记)
一.常用命令 1. cd 切换目录 cd ./* 当前目录cd /* 绝对路径cd .. 返回上一级目录cd ~ 回到当前目录pwd …...

【史上最全面esp32教程】点灯大师篇
文章目录前言ESP32简介认识arduino的两个函数点灯步骤函数介绍LED灯闪烁流水灯总结前言 esp32有很多的功能,例如wifi,蓝牙等,这节我们学习最简单的点灯。 提示:以下是本篇文章正文内容,下面案例可供参考 ESP32简介 …...
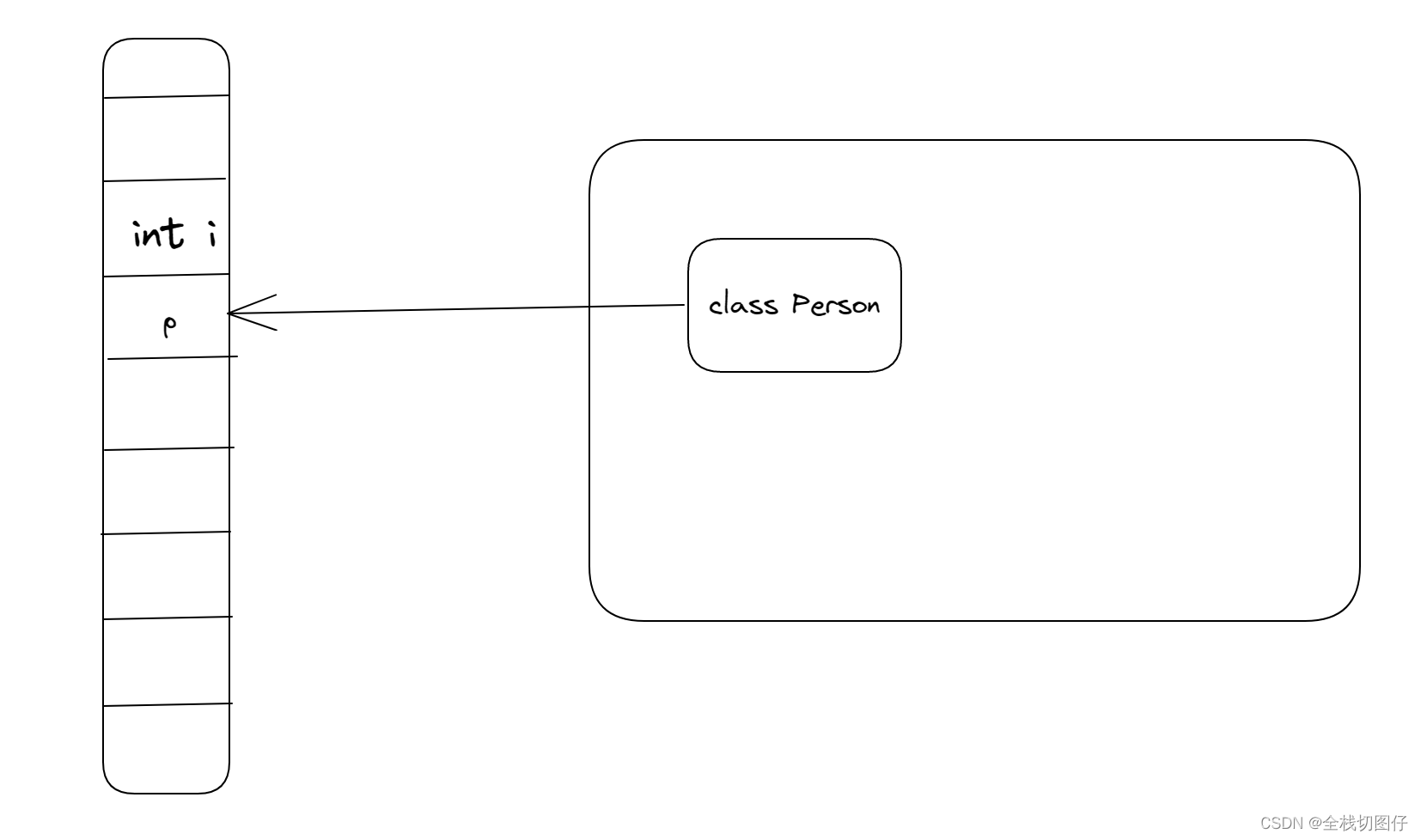
【Java 面试合集】内存中为什么要区分栈和堆
内存中为什么要区分栈和堆 1. 概述 嗨,大家好Java 面试合集又来了,今天我们分享的主题很大众化以及普通。无论是Java 语言本身还是别的语言都会有所涉及,但是今天我们从Java角度来讲下 2. 分析 今天我们会从多个方向来分享这个话题 2.1 栈是…...
【NLP实战】Python字符串处理
一、Python字符串基本操作 1. 去掉前后的特殊字符(strip) Python的strip操作可以去除字符串前后的空格(不改变原串)下例将前后的空格均删掉👇 str 人工智能 str.strip() # OUT:人工智能rstrip删除右边的空格&a…...
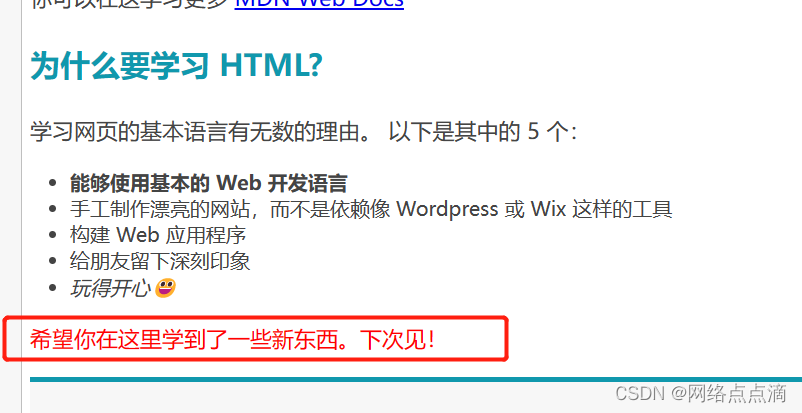
17.CSS伪类
举一个简单的例子来说明什么是伪类? 从之前的代码中,如下图,我们像给这两个列表中的某一列单独设置样式,我们该如何做呢? 我们肯定会选择在li标签上添加class去实现,如下 开始标记结束标记实际元素 <…...

数据链路层
一.以太网数据链路层考虑的是相邻两个节点(通过网线/光纤、无线直接相连的两个设备)之间的传输,这里的典型协议中最知名的就是“以太网”这个协议了数据链路层,也规定了物理层的内容以太网帧格式:IP地址用来描述整个传…...

投票需要什么流程微信投票互助平台的免费投票平台搭建
“最美家政人”网络评选投票_免费小程序投票推广_小程序投票平台好处手机互联网给所有人都带来不同程度的便利,而微信已经成为国民的系统级别的应用。现在很多人都会在微信群或朋友圈里转发投票,对于运营及推广来说找一个合适的投票小程序能够提高工作效…...

数据结构——算法的时间复杂度
🌇个人主页:_麦麦_ 📚今日名言:生命中曾经有过的所有灿烂,都终究需要用寂寞来偿还。——《百年孤独》 目录 一、前言 二、正文 1.算法效率 1.1如何衡量一个算法的好坏 1.2算法的复杂度 2. 时间复杂度 2.1时间复杂度的…...

Go基础-类型
文章目录1 bool2 有符号整数3 无符号整数4 浮点数5 复数6 string7 关于类型转型1 bool bool类型有两个值,一个是true,一个是false。 测试 package mainimport "fmt"func main() {a : trueb : falsec : a && bd : a || bfmt.Println(a…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...
