信源分类及数学模型
本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:information-theory】,需要的朋友们自取。或者公众号【AIShareLab】回复 信息论 也可获取。
文章目录
- 信源分类
- 按照信源输出的信号取值分类
- 按照信源输出信号(符号间)的依赖关系
- 信源数学模型
- 离散信源
- 连续信源
- 单符号离散无记忆信源(DMS, Discrete memoryless source)
- 单个连续变量信源
- 多维离散无记忆信源
- 离散无记忆信源的扩展源
信源分类
按照信源输出的信号取值分类
1.连续(模拟)信源:
2.离散(数字)信源:

信源输出的信号是随机信号。
按照信源输出信号(符号间)的依赖关系
1、无记忆信源: 信源先后发出的符号相互统计独立,具有相同的概率分布;
2、有记忆信源: 信源先后发出的符号相互依赖。
连续信源是有记忆信源。
信源数学模型
信源:产生随机变量、随机序列和随机过程的信号源。
- 在通信系统中收信者在未收到消息以前对信源发出什么消息是不确定的,是随机的,所以可用随机变量、随机序列或随机过程来描述信源输出的消息,或者说用一个样本空间及其概率测度——概率空间来描述信源
信源的基本特性:具有随机不确定性。
香农信息论的基本观点
- 用随机变量或随机矢量来表示信源
- 用概率论和随机过程的理论来研究信息
离散信源
用离散随机变量X表示单符号离散信源(一个符号表示一完整消息,符号取值可列),X的可能取值为信源发出的各种不同符号,X的概率分布为各符号的先验概率。
例:信源 X 的取值有 NNN 个, x1,x2,…,xNx_{1}, x_{2}, \ldots, x_{N}x1,x2,…,xN , 称为信源字符集,各符号概率分布 P(x1),P(x2),…,P(xn)P\left(x_{1}\right), P\left(x_{2}\right), \ldots, P\left(x_{n}\right)P(x1),P(x2),…,P(xn) 且 ΣiP(xi)=1\Sigma_{i} P\left(x_{i}\right)=1ΣiP(xi)=1
连续信源
信源的取值为无穷不可数的连续值,其概率分布用概率密度函数p(x)表示,且
∫−∞∞p(x)dx=1\int_{-\infty}^{\infty} p(x) d x=1 ∫−∞∞p(x)dx=1
单符号离散无记忆信源(DMS, Discrete memoryless source)
如果信源 X\mathbf{X}X 的符号集 A={x1,…,xn}\mathbf{A}=\{\mathbf{x}_{1}, \ldots, \mathbf{x}_{\mathrm{n}}\}A={x1,…,xn} , 信源在离散时间发出单个符号, 且符号发生的概率相互独立, 称为单符号离散无记忆信源, 数学模型为:
[XP]=[x1⋯xnp(x1)⋯p(xn)]p(xi)≥0,∑i=1np(xi)=1\begin{array}{l} {\left[\begin{array}{l} X \\ P \end{array}\right]=\left[\begin{array}{ccc} x_{1} & \cdots & x_{n} \\ p\left(x_{1}\right) & \cdots & p\left(x_{n}\right) \end{array}\right]} \\ p\left(x_{i}\right) \geq 0, \quad \sum_{i=1}^{n} p\left(x_{i}\right)=1 \end{array} [XP]=[x1p(x1)⋯⋯xnp(xn)]p(xi)≥0,∑i=1np(xi)=1
其中 p(xi)p\left(x_{\mathrm{i}}\right)p(xi) 成为符号 xix_{\mathrm{i}}xi 的先验概率。
Example1:一个二元无记忆信源, 符号集 A={0,1} , p 为 X=0 的概率, q 为 X=1 的概率, q=1-p ; 请写出该信源的模型。
解:信源模型为[XP]=[01pq]\left[\begin{array}{l} X \\ P \end{array}\right]=\left[\begin{array}{ll} 0 & 1 \\ p & q \end{array}\right][XP]=[0p1q]
单个连续变量信源
[XP]=[x∈(a,b)p(x)],∫abp(x)dx=1\left[\begin{array}{l} X \\ P \end{array}\right]=\left[\begin{array}{c} x \in(a, b) \\ p(x) \end{array}\right], \quad \int_{a}^{b} p(x) d x=1[XP]=[x∈(a,b)p(x)],∫abp(x)dx=1,其中 p(x)≥0p(x) \geq 0p(x)≥0 为信源输出的概率密度函数
多维离散无记忆信源
若一个信源输出是一系列离散的符号, 而每个符号又是随机的, 即信源输出为一系列随机变量 (随机矢量), 从而信源的输出可用 L 维随机矢量 [X1,X2,…,XL]\left[X_{1}, X_{2}, \ldots, X_{L}\right][X1,X2,…,XL] 来描述, 其中 L\boldsymbol{L}L 为有限正整数或可数 的无限值。
上述随机矢量中, 若每个随机变量 Xi(i=1,2,…,L)X_{i}(\boldsymbol{i}=1,2, \ldots, L)Xi(i=1,2,…,L) 都是离散的, 则可用 L 维离散概率空间来描述这类信源。
即若 L\boldsymbol{L}L 维随机矢量 X=[X1X2…XL],XiX=\left[X_{1} X_{2} \ldots X_{L}\right], X_{\mathrm{i}}X=[X1X2…XL],Xi 的具体取值为 x∈(a1,a2,…an,)x \in\left(a_{1}, a_{2}, \ldots a_{n},\right)x∈(a1,a2,…an,) , 对应概率为 PX(x)=P(x1x2…xL)P_{X}(x)=P\left(x_{1} x_{2} \ldots x_{L}\right)PX(x)=P(x1x2…xL) 为 L\boldsymbol{L}L 维联合概率分布, 则该信源的数学模型为
(XLP(x))=((a1a1…a1)…(a1a2…am)…(anan…an)P(a1a1…a1)…P(a1a2…am)…P(anan…an))\begin{array}{l} \left(\begin{array}{c} X^{L} \\ P(x) \end{array}\right) =\left(\begin{array}{ccccc} \left(a_{1} a_{1} \ldots a_{1}\right) & \ldots & \left(a_{1} a_{2 \ldots} a_{m}\right) & \ldots & \left(a_{n} a_{n} \ldots a_{n}\right) \\ P\left(a_{1} a_{1} \ldots a_{1}\right) & \ldots & P\left(a_{1} a_{2 \ldots} a_{m}\right) & \ldots & P\left(a_{n} a_{n} \ldots a_{n}\right) \end{array}\right) \end{array} (XLP(x))=((a1a1…a1)P(a1a1…a1)……(a1a2…am)P(a1a2…am)……(anan…an)P(anan…an))
其中离散消息序列长度为 L\boldsymbol{L}L , 序列每符号有 n\boldsymbol{n}n 种取值, 整个消息序列共有 nLn^{L}nL 种取值。
当输出序列中的前后消息(符号)相互统计独立, 且具有相同的概率分布, 则 L 维随机矢量的联合概率分布满足
P(X)=∏i=1LP(Xi=xj),j=1,2,…,nP(X)=\prod_{i=1}^{L} P\left(X_{i}=x_{\boldsymbol{j}}\right), \boldsymbol{j}=1,2, \ldots, n P(X)=i=1∏LP(Xi=xj),j=1,2,…,n
即 L\boldsymbol{L}L 维随机矢量的联合概率分布可用随机矢量中单个随机变量的概率乘积来表示。这种信源为离散无记忆信源。
离散无记忆信源的扩展源
设信源为 X\mathrm{X}X , 则由 X\mathrm{X}X 构成 N 维随机矢量集合 XN=[X1X2…XN],(\mathbf{X}^{N}=\left[X_{1} X_{2} \ldots X_{N}\right], \quad\left(\right.XN=[X1X2…XN],( 其中 Xi\mathbf{X}_{\mathbf{i}}Xi 与 X\mathbf{X}X 同分布, 取自同一信源 X ),称为信源 X\mathrm{X}X 的 N 次扩展源。
Example2:求例1中信源的二次扩展源模型:
Ex1\mathbf{E x} 1Ex1 的二元无记忆信源模型为[XP]=[01pq]\left[\begin{array}{l} X \\ P \end{array}\right]=\left[\begin{array}{ll} 0 & 1 \\ p & q \end{array}\right][XP]=[0p1q]
其二次扩展信源为
[X2p(α)]=[α1(00)α2(01)α3(10)α4(11)p(α1)p(α2)p(α3)p(α4)]p(α1)=p2,p(α2)=p(1−p)=p(α3)p(α4)=(1−p)2\left[\begin{array}{l}X^{2} \\ p(\alpha)\end{array}\right]=\left[\begin{array}{llll}\alpha_{1}(00) & \alpha_{2}(01) & \alpha_{3}(10) & \alpha_{4}(11) \\ p\left(\alpha_{1}\right) & p\left(\alpha_{2}\right) & p\left(\alpha_{3}\right) & p\left(\alpha_{4}\right)\end{array}\right] \\ p\left(\alpha_{1}\right)=p^{2}, p\left(\alpha_{2}\right)=p(1-p)=p\left(\alpha_{3}\right) p\left(\alpha_{4}\right)=(1-p)^{2}[X2p(α)]=[α1(00)p(α1)α2(01)p(α2)α3(10)p(α3)α4(11)p(α4)]p(α1)=p2,p(α2)=p(1−p)=p(α3)p(α4)=(1−p)2
一个离散无记忆信源的 N\mathbf{N}N 次扩展信源描述如下:
设 X\mathbf{X}X 为离散无记忆信源, 则 X\mathbf{X}X 的 N\mathbf{N}N 次扩展信源记为XN,XN=[X1X2…XN]\mathbf{X}^{N} , \mathbf{X}^{N}=\left[X_{1} X_{2} \ldots X_{N}\right]XN,XN=[X1X2…XN] , 其模型为
(XNP)=(a1⋯aMp(a1)⋯p(aM))\left(\begin{array}{c} \mathbf{X}^{N} \\ P \end{array}\right)=\left(\begin{array}{ccc} a_{1} & \cdots & a_{M} \\ p\left(a_{1}\right) & \cdots & p\left(a_{M}\right) \end{array}\right) (XNP)=(a1p(a1)⋯⋯aMp(aM))
每个 XiX_{i}Xi 取自同一个字母表 A={a1,a2,…,aN}A=\{a_{1}, a_{2}, \ldots, a_{N}\}A={a1,a2,…,aN} , 且 XiX_{i}Xi 与 X\mathbf{X}X 同分布,因此, XN\mathbf{X}^{\mathrm{N}}XN 的符号集为 AN={a1,…,aN},ajA^{N}=\{\boldsymbol{a}_{1}, \ldots, \boldsymbol{a}^{N}\}, \boldsymbol{a}_{j}AN={a1,…,aN},aj 为多维信源中的一个矢量, 即 aj∈ANa_{j} \in A^{N}aj∈AN , 矢量的个数为nNn^{N}nN,aj=(aj1aj2,…,,ajN)\boldsymbol{a}_{\boldsymbol{j}}=\left(a_{j_{1}} a_{j_{2}, \ldots,}, a_{j N}\right)aj=(aj1aj2,…,,ajN),ajka_{j k}ajk 为 $\boldsymbol{a}_{j} $的第 k\mathbf{k}k 个分量, 且 p(aj)=∏k=1Npjkp\left(\boldsymbol{a}_{j}\right)=\prod_{k=1}^{N} p_{j k}p(aj)=∏k=1Npjk ,pjkp_{j k}pjk 为第 j\mathrm{j}j 个矢量第 k\mathrm{k}k 个分量取符号 ajk\boldsymbol{a}_{\mathrm{jk}}ajk 的概率。
参考文献:
- Proakis, John G., et al. Communication systems engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- Proakis, John G., et al. SOLUTIONS MANUAL Communication Systems Engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- 周炯槃. 通信原理(第3版)[M]. 北京:北京邮电大学出版社, 2008.
- 樊昌信, 曹丽娜. 通信原理(第7版) [M]. 北京:国防工业出版社, 2012.
相关文章:

信源分类及数学模型
本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:information-theory】,需要的朋友们自取。或者公众号【AIShareLab】回复 信息论 也可获取。 文章目录信源分类按照信源…...
Games101-202作业1
一. 将模型从模型空间变换到世界空间下 在这个作业下,我们主要进行旋转的变换。 二.视图变换 ,将相机移动到坐标原点,同时保证物体和相机进行同样的变换(这样对形成的图像没有影响) 在这个作业下我们主要进行摄像机的平移变换&am…...
Linux系统之终端管理命令的基本使用
Linux系统之终端管理命令的基本使用一、检查本地系统环境1.检查系统版本2.检查系统内核版本二、终端介绍1.终端简介2.Linux终端简介3.终端的发展三、终端的相关术语1.终端模拟器2.tty终端3.pts终端4.pty终端5.控制台终端四、终端管理命令ps1.直接使用ps命令2.列出登录详细信息五…...

【Mongoose笔记】MQTT 服务器
【Mongoose笔记】MQTT 服务器 简介 Mongoose 笔记系列用于记录学习 Mongoose 的一些内容。 Mongoose 是一个 C/C 的网络库。它为 TCP、UDP、HTTP、WebSocket、MQTT 实现了事件驱动的、非阻塞的 API。 项目地址: https://github.com/cesanta/mongoose学习 下面…...

数据结构概述
逻辑结构 顺序存储 随机访问是可以通过下标取到任意一个元素,即数组的起始位置下标 链式存储 链式存储是不连续的,比如A只保留了当前的指针,那么怎么访问到B和C呢 每个元素不仅存储自己的值还使用额外的空间存储指针指向下一个元素的地址&a…...
【前端】Vue3+Vant4项目:旅游App-项目总结与预览(已开源)
文章目录项目预览首页Home日历:日期选择开始搜索位置选择上搜索框热门精选-房屋详情1热门精选-房屋详情2其他页面项目笔记项目代码项目数据项目预览 启动项目: npm run dev在浏览器中F12: 首页Home 热门精选滑动到底部后会自动加载新数据&a…...
51单片机蜂鸣器的使用
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录前言一、有源蜂鸣器和无源蜂鸣器的区别二、代码编写总结前言 本文旨在介绍如何使用51单片机驱动蜂鸣器。 一、有源蜂鸣器和无源蜂鸣器的区别 有源蜂鸣器是一种电子…...

算法练习-链表(二)
算法练习-链表(二) 文章目录算法练习-链表(二)1. 奇偶链表1.1 题目1.2 题解2. K 个一组翻转链表2.1 题目2.2 题解3. 剑指 Offer 22. 链表中倒数第k个节点3.1 题目3.2 题解3.2.1 解法13.2.2 解法24. 删除链表的倒数第 N 个结点4.1 …...
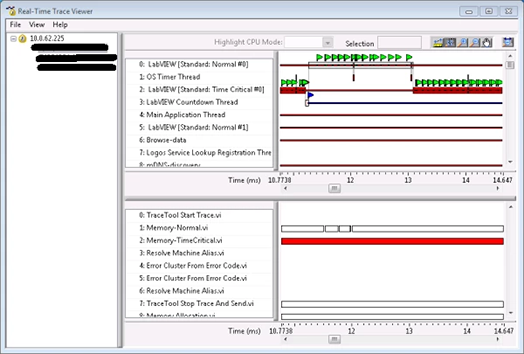
LabVIEW使用实时跟踪查看器调试多核应用程序
LabVIEW使用实时跟踪查看器调试多核应用程序随着多核CPU的推出,开发人员现在可以在LabVIEW的帮助下充分利用这项新技术的功能。并行编程在为多核CPU开发应用程序时提出了新的挑战,例如同步多个线程对共享内存的并发访问以及处理器关联。LabVIEW可自动处理…...

【go语言grpc之client端源码分析二】
go语言grpc之server端源码分析二DialContextparseTargetAndFindResolvergetResolvernewCCResolverWrapperccResolverWrapper.UpdateStatecc.maybeApplyDefaultServiceConfigccBalancerWrapper.updateClientConnState上一篇文章分析了ClientConn的主要结构体成员,然后…...

centos7安装RabbitMQ
1、查看本机基本信息 查看Linux发行版本 uname -a # Linux VM-0-8-centos 3.10.0-1160.11.1.el7.x86_64 #1 SMP Fri Dec 18 16:34:56 UTC 2020 x86_64 x86_64 x86_64 GNU/Linux cat /etc/redhat-release # CentOS Linux release 7.9.2009 (Core)2、创建创建工作目录 mkdir /…...
node基于springboot 口腔卫生防护口腔牙科诊所管理系统
目录 1 绪论 1 1.1课题背景 1 1.2课题研究现状 1 1.3初步设计方法与实施方案 2 1.4本文研究内容 2 2 系统开发环境 4 2.1 JAVA简介 4 2.2MyEclipse环境配置 4 2.3 B/S结构简介 4 2.4MySQL数据库 5 2.5 SPRINGBOOT框架 5 3 系统分析 6 3.1系统可行性分析 6 3.1.1经济可行性 6 3.…...
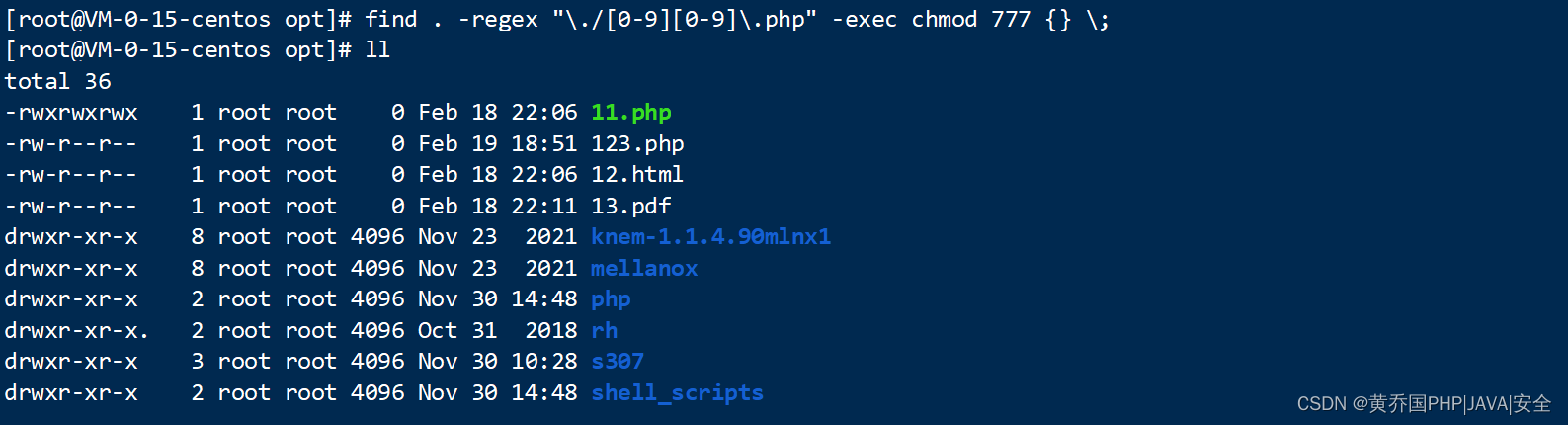
Linux常用命令之find命令详解
简介 find命令主要用于:用来在指定目录下查找文件。任何位于参数之前的字符串都将被视为欲查找的目录名。 如果使用该命令时,不设置任何参数,则find命令将在当前目录下查找子目录与文件。并且将查找到的子目录和文件全部进行显示。 是我们在…...

CMake 入门学习4 软件包管理
CMake 入门学习4 软件包管理一、Linux下的软件包管理1. 检索已安装的软件包2. 让自己编译软件支持pkg-config搜索3. 在CMakeLists查找已安装的软件包二、适合Windows下的包管理工具1. vcpkg2. Conan(1) 安装Conan(2) 配置Conan(3) 创建工程(4) 安装依赖库(5) 使用依赖库三、CMa…...

【数据库数据乱码错误】存进去的数据乱码(???)
目录 1.当我新增一条数据的时候,成功后查看数据库中的数据时,竟然变成???乱码格式了: 2.那么问题有3处需要注意: 第一:settings配置 第二:POM文件 第三:…...
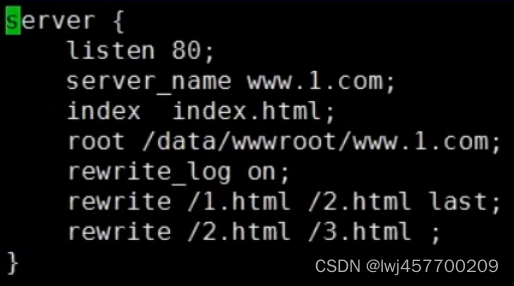
rewrite中的if、break、last
目录 rewrite 作用: 依赖: 打开重定向日志: if 判断: location {} 本身有反复匹配执行特征 在 location 中加入 break 和 last (不一样) 加了break后,立刻停止向下 且 跳出。 加了last…...

JavaSE-线程池(5)- 建议使用的方式
JavaSE-线程池(5)- 建议使用的方式 虽然JDK Executors 工具类提供了默认的创建线程池的方法,但一般建议自定义线程池参数,下面是阿里巴巴开发手册给出的理由: 另外Spring也提供了线程池的实现,比如 Thread…...

城市轨道交通供电系统研究(Matlab代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...

什么是 RESTful 风格?
一、什么是 REST ? REST即表述性状态传递(英文:Representational State Transfer,简称REST)是Roy Thomas Fielding博士在2000年他的博士论文中提出来的一种软件架构风格。它是一种针对网络应用的设计和开发方式&#…...
从业6年,对敏捷和自动化测试的一点心得
不久前,参加Thoughtworks组织的一场自动化测试的分享,同事由于出差国外不能参加,特意嘱托我提问两个问题: 在互联网这个将“敏捷”与“持续集成”进行积极实践的环境里,“敏捷测试”与“自动化测试”成了一个大家经常…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...
