常用的图像校正方法
在数字图像处理中,常用的校正方法包括明场均匀性校正、查找表(LUT)校正和伽玛(Gamma)校正。这些校正方法分别针对不同的图像问题,可以改善图像质量,提升图像的可读性和可分析性。下面是这三种校正方法的详细介绍:
1. 明场均匀性校正:
明场均匀性校正(也称为平场校正)是一种消除图像中的非均匀亮度和暗度变化的技术。这种非均匀性可能是由于照明不均、相机的光学系统或传感器特性引起的。
步骤:
-
捕获一个明场图像: 首先,在没有样本的情况下,仅保留照明源,捕获一个图像。这个图像被称为“明场图像”或“平场图像”。
-
捕获一个暗场图像(可选): 在没有照明和样本的情况下,捕获一个图像。这个图像被称为“暗场图像”。
-
校正: 使用以下公式进行校正:
[
\text{校正图像} = \frac{{\text{原始图像} - \text{暗场图像}}}{{\text{明场图像} - \text{暗场图像}}}
]其中,暗场校正是可选的。
作用: 明场均匀性校正可以消除图像中由于照明不均匀或相机系统特性引起的非均匀性,得到一幅具有均匀亮度的图像。
2. LUT(Look-Up Table)校正:
LUT校正是通过预定义一个查找表来改变图像像素值的一种方法。每个输入像素值都有一个预定的输出值。
步骤:
- 创建LUT: 创建一个查找表,该表定义了每个可能的输入像素值与一个特定的输出像素值之间的映射关系。
- 应用LUT: 对于图像中的每一个像素,找到其对应的LUT中的值,并替换原像素值。
作用: LUT校正可以用来改变图像的对比度和亮度,实现特定的图像效果,或对图像进行线性或非线性变换。
3. Gamma 校正:
伽玛校正是用来校正图像亮度的非线性变换。它是通过应用以下公式进行的:
[
\text{输出像素值} = A \cdot (\text{输入像素值})^\gamma
]
其中,( A ) 是一个常数,( \gamma ) 是伽玛值。
作用:
- 改善图像亮度: 对于暗的图像,伽玛校正可以增加亮度,使图像看起来更亮。
- 适应人眼感知: 伽玛校正可以使图像的亮度分布更接近人眼的感知特性,从而改善图像的视觉效果。
这些校正方法是图像处理中常用的基本技术,它们可以独立使用,也可以组合使用,以满足不同的图像处理需求。
相关文章:

常用的图像校正方法
在数字图像处理中,常用的校正方法包括明场均匀性校正、查找表(LUT)校正和伽玛(Gamma)校正。这些校正方法分别针对不同的图像问题,可以改善图像质量,提升图像的可读性和可分析性。下面是这三种校…...

AWS security 培训笔记
云计算的好处 Amazon S3 (Storage) Amazon EC2 (Compute) 上图aws 的几个支柱:安全是其中一个啦 其中安全有几个方面 IAMdetection基础架构保护数据保护应急响应 关于云供应商的责任 data center 原来长这样 ,据说非常之隐蔽的 如果有天退役了…...
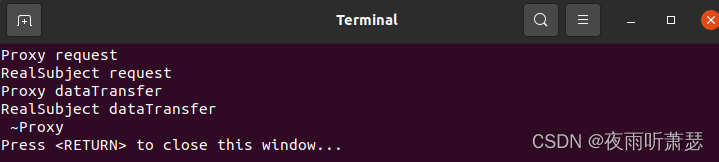
设计模式之代理模式(Proxy)的C++实现
1、代理模式的提出 在组件的开发过程中,有些对象由于某种原因(比如对象创建的开销很大,或者对象的一些操作需要做安全控制,或者需要进程外的访问等),会使Client使用者在操作这类对象时可能会存在问题&…...
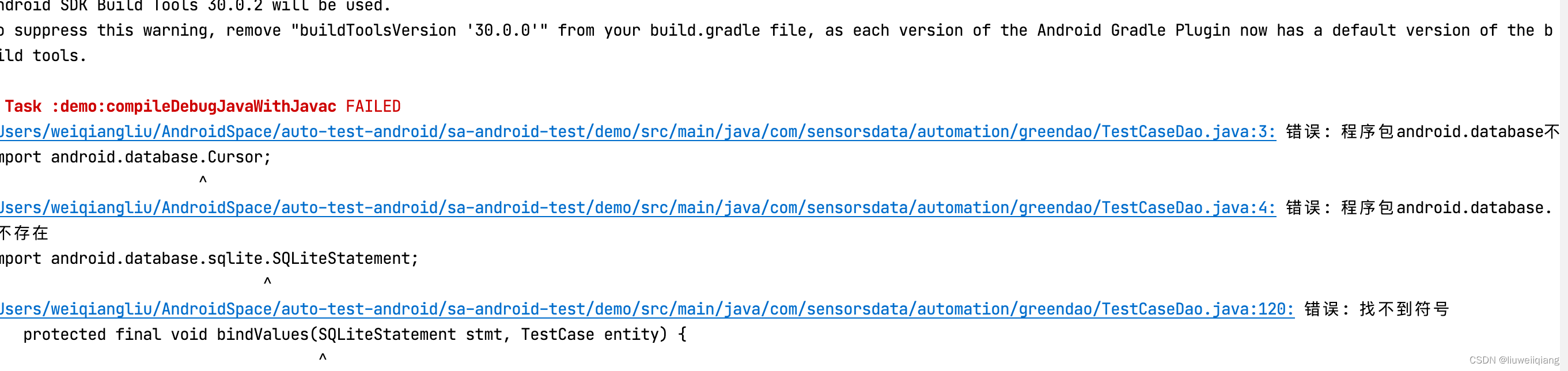
vim 配置环境变量与 JDK 编译器异常
vim 配置环境变量 使用 vim 打开系统中的配置信息(不存在将会创建): vim ~/.bash_profile 以配置两个版本 JDK 为例(前提是已安装 JDK),使用上述命令打开配置信息: 输入法调成英文,输入 i&…...

TiDB v7.1.0 跨业务系统多租户解决方案
本文介绍了 TiDB 数据库的资源管控技术,并通过业务测试验证了效果。资源管控技术旨在解决多业务共用一个集群时的资源隔离和负载问题,通过资源组概念,可以限制不同业务的计算和 I/O 资源,实现资源隔离和优先级调度,提高…...
)
【题解】二叉树中和为某一值的路径(一)
二叉树中和为某一值的路径(一) 题目链接:二叉树中和为某一值的路径(一) 解题思路1:递归 我们或许想记录下每一条从根节点到叶子节点的路径,计算出该条路径的和,但此种思路用递归稍麻烦,我们可以试着把和转换为差&am…...

css中变量和使用变量和运算
变量: 语法:--css变量名:值; --view-theme: #1a99fb; css使用变量: 语法:属性名:var( --css变量名 ); color: var(--view-theme); css运算: 语法:属性名…...

数据结构之线性表的类型运用Linear Lists: 数组,栈,队列,链表
线性表 定义 一个最简单,最基本的数据结构。一个线性表由多个相同类型的元素穿在一次,并且每一个元素都一个前驱(前一个元素)和后继(后一个元素)。 线性表的类型 常见的类型:数组、栈、队列…...

成瘾机制中微生物群的神秘角色
谷禾健康 成瘾是一种大脑疾病,受害者无法控制地对某种物质或行为产生强烈的依赖和渴求,尽管这种行为会产生有害的后果。成瘾包括一系列物质滥用障碍,例如药物、酒精、香烟,过度饮食。近年来,吸毒成瘾急剧上升ÿ…...
arm安装docker与docker-copose
一、银河麒麟Arm64安装docker 1、docker 安装包地址: https://download.docker.com/linux/static/stable 2、解压,然后将docker目录下文件拷贝到/usr/bin里 tar -xf docker-18.09.3.tgz mv docker/* /usr/bin/ 3、准备 docker.service系统配置文件 &…...

9.文件基本操作
第四章 文件管理 9.文件基本操作 “打开文件和关闭文件”与平常鼠标双击打开文件和点击“X”关闭文件是有所不同的。 操作系统在处理open系统调用时主要做了以下两件事情,①根据我们提供的文件存放路径在外存当中找到这个目录对应的目录表&#x…...

【Java】Spring——Bean对象的作用域和生命周期
文章目录 前言一、引出Bean对象的作用域1.普通变量的作用域2.Bean对象的作用域 二、Bean对象的作用域1.Bean对象的6种作用域2.设置Bean对象的作用域 三、Bean对象的生命周期总结 前言 本人是一个普通程序猿!分享一点自己的见解,如果有错误的地方欢迎各位大佬莅临指导,如果你也…...

数字孪生助力智慧水务:科技创新赋能水资源保护
智慧水务中,数字孪生有着深远的作用,正引领着水资源管理和环境保护的创新变革。随着城市化和工业化的不断推进,水资源的可持续利用和管理愈发显得重要,而数字孪生技术为解决这一挑战提供了独特的解决方案。 数字孪生技术…...

css 实现文字横向循环滚动
实现效果 思路 ## 直接上代码,html部分 //我这里是用的uniapp <view class"weather_info_wrap"><view class"weather_info">当前多云,今晚8点转晴,明天有雨,温度32摄氏度。</view><view class&qu…...

VuePress 数学公式支持
前言 博主在为 VuePress1.0 博客添加数学公式支持过程中遇到如下问题 问题一 在配置诸如 markdown-it-texmath,markdown-it-katex,markdown-it-mathjax3 这些插件后遇到 Error: Dynamic require of "XXX" is not supported 问题二 配置插件 vuepress-plugin-ma…...
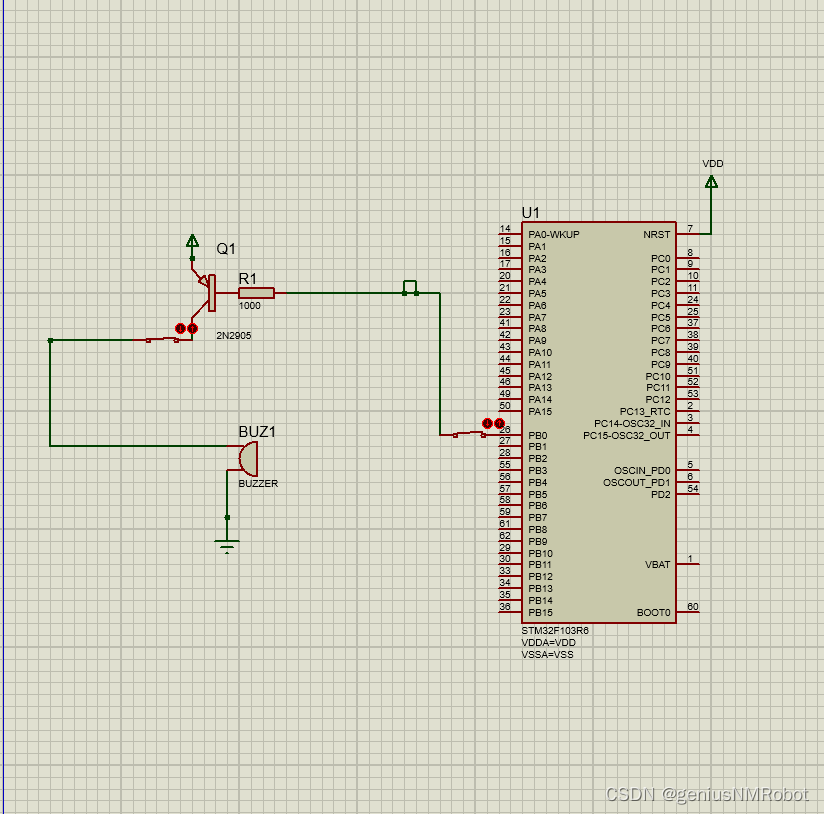
stm32控制蜂鸣器源代码(附带proteus线路图)
说明: 1 PB0输出0时,蜂鸣器发生; 2 蜂鸣器电阻值如果太大会导致电流太小,发不出声音; 3蜂鸣器额定电压需要设置得低一点,可以是2V,但不能高于3V,这更右上角的电阻值有关系&#x…...

selinux
一、selinux的说明 二、selinux的工作原理 三、selinux的启动、关闭与查看 Enforcing和permissive都是临时的,重启还是依据配置文件中,禁用selinux,修改配置文件: 之后重启生效 四、selinux对linux服务的影响...

使用opencv4.7.0部署yolov5
yolov5原理和部署原理就不说了,想了解的可以看看这篇部署原理文章 #include <fstream> #include <sstream> #include <iostream> #include <opencv2/dnn.hpp> #include <opencv2/imgproc.hpp> #include <opencv2/highgui.hpp>/…...
Python - 协程基本使用详解【demo】
一. 前言 协程(Coroutine)是一种轻量级的线程,也被称为用户级线程或绿色线程。它是一种用户态的上下文切换方式,比内核态的线程切换更为轻量级,能够高效的支持大量并发操作。 2. 使用协程的好处 Python 中的协程是通…...

Android MVVM架构模式,详详详细学习
MVVM(Model-View-ViewModel) 是一种基于数据绑定的架构模式,用于设计和组织应用程序的代码结构。它将应用程序分为三个主要部分:Model(模型)、View(视图)和ViewModel(视…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...

【java】【服务器】线程上下文丢失 是指什么
目录 ■前言 ■正文开始 线程上下文的核心组成部分 为什么会出现上下文丢失? 直观示例说明 为什么上下文如此重要? 解决上下文丢失的关键 总结 ■如果我想在servlet中使用线程,代码应该如何实现 推荐方案:使用 ManagedE…...
