机器学习笔记之优化算法(十五)Baillon Haddad Theorem简单认识
机器学习笔记之优化算法——Baillon Haddad Theorem简单认识
引言
本节将简单认识 Baillon Haddad Theorem \text{Baillon Haddad Theorem} Baillon Haddad Theorem(白老爹定理),并提供相关证明。
Baillon Haddad Theorem \text{Baillon Haddad Theorem} Baillon Haddad Theorem简单认识
如果函数 f ( ⋅ ) f(\cdot) f(⋅)在其定义域内可微,并且是凸函数,则存在如下等价条件:
以下几个条件之间相互等价。
-
关于 f ( ⋅ ) f(\cdot) f(⋅)的梯度 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)满足 L \mathcal L L-利普希兹连续;
{ ∀ x , x ^ ∈ R n , ∃ L : s . t . ∣ ∣ f ( x ) − f ( x ^ ) ∣ ∣ ≤ L ⋅ ∣ ∣ x − x ^ ∣ ∣ ∃ ξ ∈ ( x , x ^ ) ⇒ ∣ ∣ f ( x ) − f ( x ^ ) ∣ ∣ ∣ ∣ x − x ^ ∣ ∣ = f ′ ( ξ ) ≤ L \begin{cases} \forall x,\hat x \in \mathbb R^n ,\exist \mathcal L: \quad s.t.||f(x) - f(\hat x)|| \leq \mathcal L \cdot ||x - \hat x|| \\ \quad \\ \begin{aligned} \exist \xi \in (x,\hat x) \Rightarrow \frac{||f(x) - f(\hat x)||}{||x - \hat x||} = f'(\xi) \leq \mathcal L \end{aligned} \end{cases} ⎩ ⎨ ⎧∀x,x^∈Rn,∃L:s.t.∣∣f(x)−f(x^)∣∣≤L⋅∣∣x−x^∣∣∃ξ∈(x,x^)⇒∣∣x−x^∣∣∣∣f(x)−f(x^)∣∣=f′(ξ)≤L
关于利普希兹连续详见二次上界引理。从逻辑的角度理解,这意味着:函数 f ( ⋅ ) f(\cdot) f(⋅)中斜率的变化量被利普希兹常数 L \mathcal L L约束。从图像的角度模糊观察,由于 L \mathcal L L的限制,不会出现斜率过于陡峭的情况。
见下图。从x ⇒ y x \Rightarrow y x⇒y的过程中,∇ f ( x ) ⇒ ∇ f ( y ) \nabla f(x) \Rightarrow \nabla f(y) ∇f(x)⇒∇f(y)发生了剧烈的变化。这本质上说明f ( ⋅ ) f(\cdot) f(⋅)在[ x , y ] [x,y] [x,y]区间内过于陡峭的原因。

-
关于函数 G ( x ) = L 2 x T x − f ( x ) \begin{aligned}\mathcal G(x) = \frac{\mathcal L}{2} x^T x - f(x)\end{aligned} G(x)=2LxTx−f(x)同样是凸函数。
观察 G ( x ) \mathcal G(x) G(x),可以发现它由两部分组成:系数是 L 2 \begin{aligned}\frac{\mathcal L}{2}\end{aligned} 2L,关于变量 x x x的二次项结果;以及 f ( x ) f(x) f(x)自身。而二次函数 L 2 x T x \begin{aligned}\frac{\mathcal L}{2}x^Tx\end{aligned} 2LxTx其自身一定是个凸函数。该条件意味着:这两个凸函数的差也是凸函数。
如果从逻辑角度对 L 2 x T x − f ( x ) \begin{aligned}\frac{\mathcal L}{2}x^Tx - f(x)\end{aligned} 2LxTx−f(x)进行认知:两个凸函数之间做减法,若 f ( x ) f(x) f(x)的陡峭程度要高于 L 2 x T x \begin{aligned}\frac{\mathcal L}{2}x^Tx\end{aligned} 2LxTx,这势必使得减法结果可能不是凸函数;因而该等价条件的本质依然是:约束 f ( x ) f(x) f(x)斜率的变化率,而该变化率的约束与利普希兹常数 L \mathcal L L存在关联关系。
-
关于函数的梯度 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)具有余强制性 ( Co-coercive ) (\text{Co-coercive}) (Co-coercive)。即:
[ ∇ f ( x ) − ∇ f ( y ) ] T ( x − y ) ≥ 1 L ∣ ∣ ∇ f ( x ) − ∇ f ( y ) ∣ ∣ 2 \left[\nabla f(x) - \nabla f(y)\right]^T(x - y) \geq \frac{1}{\mathcal L} ||\nabla f(x) - \nabla f(y)||^2 [∇f(x)−∇f(y)]T(x−y)≥L1∣∣∇f(x)−∇f(y)∣∣2
首先解释一下强制性 ( Coercive ) (\text{Coercive}) (Coercive)。它也被称作强单调性 ( Strongly monotonicity ) (\text{Strongly monotonicity}) (Strongly monotonicity)。从名字可以看出来——它比一般的单调性更强。关于 f ( ⋅ ) : R ↦ R f(\cdot) :\mathbb R \mapsto \mathbb R f(⋅):R↦R,其单调性的定义表示为:自变量的差异性与对应函数差异性之间同号。关于n n n维的特征空间f ( ⋅ ) : R n ↦ R n f(\cdot):\mathbb R^n \mapsto \mathbb R^n f(⋅):Rn↦Rn,那么此时的f ( x ) − f ( y ) f(x) - f(y) f(x)−f(y)与x − y x - y x−y都是向量。对应单调性的定义即:[ f ( x ) − f ( y ) ] T ( x − y ) ≥ 0 [f(x) - f(y)]^T(x - y) \geq 0 [f(x)−f(y)]T(x−y)≥0
∀ x , y ∈ R s . t . [ f ( x ) − f ( y ) ] ⋅ ( x − y ) ≥ 0 \forall x,y \in \mathbb R \quad s.t. [f(x) - f(y)] \cdot (x - y) \geq 0 ∀x,y∈Rs.t.[f(x)−f(y)]⋅(x−y)≥0
而强单调性在单调性同号的基础上,进行了更强的约束:将式子右侧的 0 0 0替换为一个恒正的值。该值通常表示为:系数 α \alpha α与 x x x的增量 ∣ ∣ x − y ∣ ∣ 2 ||x - y||^2 ∣∣x−y∣∣2的乘积形式:
[ f ( x ) − f ( y ) ] T ( x − y ) ≥ α ⋅ ∣ ∣ x − y ∣ ∣ 2 [f(x) - f(y)]^T (x - y) \geq \alpha \cdot ||x - y||^2 [f(x)−f(y)]T(x−y)≥α⋅∣∣x−y∣∣2
若该值使用 f ( x ) f(x) f(x)的增量进行表示,我们称之为余强制性,也被称作逆向强单调性 ( Inverse Strongly monotonicity ) (\text{Inverse Strongly monotonicity}) (Inverse Strongly monotonicity):
[ f ( x ) − f ( y ) ] T ( x − y ) ≥ α ⋅ ∣ ∣ f ( x ) − f ( y ) ∣ ∣ 2 [f(x) - f(y)]^T (x - y) \geq \alpha \cdot ||f(x) - f(y)||^2 [f(x)−f(y)]T(x−y)≥α⋅∣∣f(x)−f(y)∣∣2
回顾等价条件 3 3 3:不等式左侧就是 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)单调性的定义;不等式右侧则是关于余强制性的表述。需要关注的点在于:参与描述正值的系数 α \alpha α与利普希兹常数 L \mathcal L L之间存在关联关系: α = 1 L \begin{aligned}\alpha = \frac{1}{\mathcal L}\end{aligned} α=L1。
证明过程
通过证明:条件 1 ⇒ 1 \Rightarrow 1⇒条件 2 2 2,条件 2 ⇒ 2 \Rightarrow 2⇒条件 3 3 3,条件 3 ⇒ 3 \Rightarrow 3⇒条件 1 1 1来实现 3 3 3个条件之间的等价关系。
证明:条件 1 ⇒ 1 \Rightarrow 1⇒ 条件 2 2 2
若 f ( ⋅ ) f(\cdot) f(⋅)是凸函数,在定义域内可微;并且梯度函数 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)满足 L \mathcal L L-利普希兹连续,求证:函数 G ( x ) = L 2 x T x − f ( x ) \begin{aligned}\mathcal G(x) = \frac{\mathcal L}{2} x^Tx - f(x)\end{aligned} G(x)=2LxTx−f(x)是凸函数。
关于凸函数的一种证法在于,证明该函数的梯度满足单调性。之所以引入梯度的另一个原因是可以将 L 2 x T x \begin{aligned}\frac{\mathcal L}{2} x^Tx\end{aligned} 2LxTx化成一次项。
证明过程:由 G ( x ) = L 2 x T x − f ( x ) \begin{aligned}\mathcal G(x) = \frac{\mathcal L}{2} x^Tx -f(x)\end{aligned} G(x)=2LxTx−f(x)可知,关于 G ( x ) \mathcal G(x) G(x)梯度 ∇ G ( x ) \nabla \mathcal G(x) ∇G(x)可表示为:
∇ G ( x ) = L ⋅ x − ∇ f ( x ) \nabla \mathcal G(x) = \mathcal L \cdot x - \nabla f(x) ∇G(x)=L⋅x−∇f(x)
至此,观察 ∇ G ( x ) \nabla \mathcal G(x) ∇G(x)的单调性:
仅需证明 I ≥ 0 \mathcal I \geq 0 I≥0恒成立即可。
∀ x 1 , x 2 ∈ R n ⇒ I = [ ∇ G ( x 1 ) − ∇ G ( x 2 ) ] T ( x 1 − x 2 ) \forall x_1,x_2 \in \mathbb R^n \Rightarrow \mathcal I = [\nabla \mathcal G(x_1) - \nabla \mathcal G(x_2)]^T (x_1 - x_2) ∀x1,x2∈Rn⇒I=[∇G(x1)−∇G(x2)]T(x1−x2)
将上述梯度结果代入,有:
继续展开~
I = [ L ⋅ x 1 − ∇ f ( x 1 ) − L ⋅ x 2 + ∇ f ( x 2 ) ] T ( x 1 − x 2 ) = L ⋅ ( x 1 − x 2 ) T ( x 1 − x 2 ) − [ ∇ f ( x 1 ) − ∇ f ( x 2 ) ] T ( x 1 − x 2 ) \begin{aligned} \mathcal I & = [\mathcal L \cdot x_1 - \nabla f(x_1) - \mathcal L \cdot x_2 + \nabla f(x_2)]^T (x_1 - x_2) \\ & = \mathcal L\cdot (x_1 - x_2)^T(x_1 - x _2) - [\nabla f(x_1) - \nabla f(x_2)]^T(x_1 - x_2) \end{aligned} I=[L⋅x1−∇f(x1)−L⋅x2+∇f(x2)]T(x1−x2)=L⋅(x1−x2)T(x1−x2)−[∇f(x1)−∇f(x2)]T(x1−x2)
观察后一项: − [ ∇ f ( x 1 ) − ∇ f ( x 2 ) ] T ( x 1 − x 2 ) -[\nabla f(x_1) - \nabla f(x_2)]^T (x_1 - x_2) −[∇f(x1)−∇f(x2)]T(x1−x2),这明显是两个向量的内积形式。可以根据柯西施瓦茨不等式,得到如下结果:
该部分同样可以使用向量乘法描述: a T b = ∣ a ∣ ⋅ ∣ b ∣ ⋅ cos θ ≤ ∣ a ∣ ⋅ ∣ b ∣ a^Tb = |a|\cdot|b| \cdot \cos \theta \leq |a| \cdot |b| aTb=∣a∣⋅∣b∣⋅cosθ≤∣a∣⋅∣b∣因为 cos θ ∈ [ − 1 , 1 ] ≤ 1 \cos \theta \in [-1,1] \leq 1 cosθ∈[−1,1]≤1。
[ ∇ f ( x 1 ) − ∇ f ( x 2 ) ] T ( x 1 − x 2 ) ≤ ∣ ∣ ∇ f ( x 1 ) − ∇ f ( x 2 ) ∣ ∣ ⋅ ∣ ∣ x 1 − x 2 ∣ ∣ [\nabla f(x_1) - \nabla f(x_2)]^T(x_1 - x_2) \leq ||\nabla f(x_1) - \nabla f(x_2)|| \cdot ||x_1 - x_2|| [∇f(x1)−∇f(x2)]T(x1−x2)≤∣∣∇f(x1)−∇f(x2)∣∣⋅∣∣x1−x2∣∣
加上负号与前一项,从而有:
至于 ( x 1 − x 2 ) T ( x 1 − x 2 ) = ∣ ∣ x 1 − x 2 ∣ ∣ 2 (x_1 - x_2)^T(x_1 - x_2) = ||x_1 - x_2||^2 (x1−x2)T(x1−x2)=∣∣x1−x2∣∣2,两向量重合,夹角为 0 0 0。
I ≥ L ⋅ ∣ ∣ x 1 − x 2 ∣ ∣ 2 − ∣ ∣ ∇ f ( x 1 ) − ∇ f ( x 2 ) ∣ ∣ ⋅ ∣ ∣ x 1 − x 2 ∣ ∣ \mathcal I \geq \mathcal L \cdot ||x_1 - x_2||^2 - ||\nabla f(x_1) - \nabla f(x_2)|| \cdot ||x_1 - x_2|| I≥L⋅∣∣x1−x2∣∣2−∣∣∇f(x1)−∇f(x2)∣∣⋅∣∣x1−x2∣∣
由于梯度函数 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)满足 L \mathcal L L-利普希兹连续,因而将 ∣ ∣ ∇ f ( x 1 ) − ∇ f ( x 2 ) ∣ ∣ ≤ L ⋅ ∣ ∣ x 1 − x 2 ∣ ∣ ||\nabla f(x_1) - \nabla f(x_2)|| \leq \mathcal L \cdot ||x_1 - x_2|| ∣∣∇f(x1)−∇f(x2)∣∣≤L⋅∣∣x1−x2∣∣,对上式中的 ∣ ∣ ∇ f ( x 1 ) − ∇ f ( x 2 ) ∣ ∣ ||\nabla f(x_1) - \nabla f(x_2)|| ∣∣∇f(x1)−∇f(x2)∣∣进行替换,最终不等号的方向不发生变化:
{ − ∣ ∣ ∇ f ( x 1 ) − ∇ f ( x 2 ) ∣ ∣ ≥ − L ⋅ ∣ ∣ x 1 − x 2 ∣ ∣ I ≥ L ⋅ ∣ ∣ x 1 − x 2 ∣ ∣ 2 − ∣ ∣ ∇ f ( x 1 ) − ∇ f ( x 2 ) ∣ ∣ ⋅ ∣ ∣ x 1 − x 2 ∣ ∣ ≥ L ⋅ ∣ ∣ x 1 − x 2 ∣ ∣ 2 − ( L ⋅ ∣ ∣ x 1 − x 2 ∣ ∣ ) ⋅ ∣ ∣ ∣ x 1 − x 2 ∣ ∣ = 0 \begin{cases} -||\nabla f(x_1) - \nabla f(x_2)|| \geq -\mathcal L \cdot ||x_1 - x_2|| \\ \quad \\ \begin{aligned} \mathcal I & \geq \mathcal L \cdot ||x_1 - x_2||^2 - ||\nabla f(x_1) - \nabla f(x_2)|| \cdot ||x_1 - x_2|| \\ & \geq \mathcal L \cdot ||x_1 - x_2||^2 - (\mathcal L \cdot ||x_1 - x_2||) \cdot |||x_1 - x_2|| \\ & = 0 \end{aligned} \end{cases} ⎩ ⎨ ⎧−∣∣∇f(x1)−∇f(x2)∣∣≥−L⋅∣∣x1−x2∣∣I≥L⋅∣∣x1−x2∣∣2−∣∣∇f(x1)−∇f(x2)∣∣⋅∣∣x1−x2∣∣≥L⋅∣∣x1−x2∣∣2−(L⋅∣∣x1−x2∣∣)⋅∣∣∣x1−x2∣∣=0
最终可证明: I ≥ 0 ⇒ \mathcal I \geq 0 \Rightarrow I≥0⇒梯度函数 ∇ G ( x ) \nabla \mathcal G(x) ∇G(x)有单调性。从而函数 G ( x ) \mathcal G(x) G(x)是凸函数。
证明:条件 3 ⇒ 3 \Rightarrow 3⇒条件 1 1 1
若梯度函数 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)有余强制性,那么该梯度函数 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)满足 L \mathcal L L-利普希兹连续。
证明过程:基于 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)余强制性,结合柯西施瓦茨不等式,有:
使用柯西施瓦茨不等式将不等式左侧表示为模的乘积形式。
{ [ ∇ f ( x ) − ∇ f ( y ) ] T ( x − y ) ≥ 1 L ∣ ∣ ∇ f ( x ) − ∇ f ( y ) ∣ ∣ 2 ⇓ ∣ ∣ ∇ f ( x 1 ) − ∇ f ( x 2 ) ∣ ∣ ⋅ ∣ ∣ x 1 − x 2 ∣ ∣ ≥ [ ∇ f ( x 1 ) − ∇ f ( x 2 ) ] T ( x 1 − x 2 ) ≥ 1 L ∣ ∣ ∇ f ( x 1 ) − ∇ f ( x 2 ) ∣ ∣ 2 \begin{cases} \begin{aligned} \left[\nabla f(x) - \nabla f(y)\right]^T(x - y) & \geq \frac{1}{\mathcal L} ||\nabla f(x) - \nabla f(y)||^2 \\ & \Downarrow \\ ||\nabla f(x_1) - \nabla f(x_2)|| \cdot ||x_1 - x_2|| & \geq [\nabla f(x_1) - \nabla f(x_2)]^T (x_1 - x_2) \\ & \geq \frac{1}{\mathcal L} ||\nabla f(x_1) - \nabla f(x_2)||^2 \end{aligned} \end{cases} ⎩ ⎨ ⎧[∇f(x)−∇f(y)]T(x−y)∣∣∇f(x1)−∇f(x2)∣∣⋅∣∣x1−x2∣∣≥L1∣∣∇f(x)−∇f(y)∣∣2⇓≥[∇f(x1)−∇f(x2)]T(x1−x2)≥L1∣∣∇f(x1)−∇f(x2)∣∣2
消去 ∣ ∣ ∇ f ( x 1 ) − ∇ f ( x 2 ) ∣ ∣ ||\nabla f(x_1) - \nabla f(x_2)|| ∣∣∇f(x1)−∇f(x2)∣∣,整理有:
∣ ∣ ∇ f ( x 1 ) − ∇ f ( x 2 ) ∣ ∣ ≤ L ⋅ ∣ ∣ x 1 − x 2 ∣ ∣ ||\nabla f(x_1) - \nabla f(x_2)|| \leq \mathcal L \cdot ||x_1 - x_2|| ∣∣∇f(x1)−∇f(x2)∣∣≤L⋅∣∣x1−x2∣∣
从而得证: ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)满足 L \mathcal L L-利普希兹连续。
证明:条件 2 ⇒ 2 \Rightarrow 2⇒条件 3 3 3
若 G ( x ) = L 2 x T x − f ( x ) \begin{aligned}\mathcal G(x) = \frac{\mathcal L}{2}x^Tx - f(x)\end{aligned} G(x)=2LxTx−f(x)是凸函数,那么关于梯度函数 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)有余强制性。
证明思路:在证明之前,引入几个辅助变量:
将余强制性不等式左侧 [ ∇ f ( x 1 ) − ∇ f ( x 2 ) ] T ( x 1 − x 2 ) [\nabla f(x_1) - \nabla f(x_2)]^T (x_1 - x_2) [∇f(x1)−∇f(x2)]T(x1−x2)记作 Δ \Delta Δ,并将其分解为如下形式:
其中将x 1 − x 2 x_1 - x_2 x1−x2转化成− ( x 2 − x 1 ) -(x_2 - x_1) −(x2−x1),并将负号提出来。其中[ ∇ f ( x 1 ) − ∇ f ( x 2 ) ] T = { [ ∇ f ( x 1 ) ] T − [ ∇ f ( x 2 ) ] T } [\nabla f(x_1) - \nabla f(x_2)]^T = \left\{[\nabla f(x_1)]^T - [\nabla f(x_2)]^T\right\} [∇f(x1)−∇f(x2)]T={[∇f(x1)]T−[∇f(x2)]T}。
Δ = [ f ( x 1 ) + f ( x 2 ) ] − [ f ( x 1 ) + f ( x 2 ) ] ⏟ = 0 − { [ ∇ f ( x 1 ) ] T − [ ∇ f ( x 2 ) ] T } ( x 2 − x 1 ) = f ( x 2 ) − { f ( x 1 ) + [ ∇ f ( x 1 ) ] T ( x 2 − x 1 ) } ⏟ Δ 1 + f ( x 1 ) − { f ( x 2 ) + [ ∇ f ( x 2 ) ] T ( x 1 − x 2 ) } ⏟ Δ 2 = Δ 1 + Δ 2 \begin{aligned} \Delta & = \underbrace{[f(x_1) + f(x_2)] - [f(x_1) + f(x_2)]}_{=0} - \left\{[\nabla f(x_1)]^T - [\nabla f(x_2)]^T\right\}(x_2 - x_1) \\ & = \underbrace{f(x_2) - \{f(x_1) + [\nabla f(x_1)]^T (x_2 - x_1)\}}_{\Delta_1} + \underbrace{f(x_1) - \left\{f(x_2) + [\nabla f(x_2)]^T(x_1 - x_2)\right\}}_{\Delta_2} \\ & = \Delta_1 + \Delta_2 \end{aligned} Δ==0 [f(x1)+f(x2)]−[f(x1)+f(x2)]−{[∇f(x1)]T−[∇f(x2)]T}(x2−x1)=Δ1 f(x2)−{f(x1)+[∇f(x1)]T(x2−x1)}+Δ2 f(x1)−{f(x2)+[∇f(x2)]T(x1−x2)}=Δ1+Δ2
可以在图像中描述出 Δ 1 , Δ 2 \Delta_1,\Delta_2 Δ1,Δ2的表示:
- 其中 f ( x 1 ) + [ ∇ f ( x 1 ) ] T ( x 2 − x 1 ) f(x_1) + [\nabla f(x_1)]^T (x_2 - x_1) f(x1)+[∇f(x1)]T(x2−x1)表示过点 x 1 x_1 x1的 f ( ⋅ ) f(\cdot) f(⋅)的切线,与 x = x 2 x= x_2 x=x2相交后,到点 x 2 x_2 x2的距离。见黄色实线部分;
- 对应 Δ 1 \Delta_1 Δ1则表示: f ( x 2 ) f(x_2) f(x2)与 f ( x 1 ) + [ ∇ f ( x 1 ) ] T ( x 2 − x 1 ) f(x_1) + [\nabla f(x_1)]^T (x_2 - x_1) f(x1)+[∇f(x1)]T(x2−x1)之间的距离差值。见红色实线部分。
- 同理,关于 Δ 2 \Delta_2 Δ2的图像描述表示为:
对应的Δ 2 \Delta_2 Δ2表示为图中的绿色实线部分。
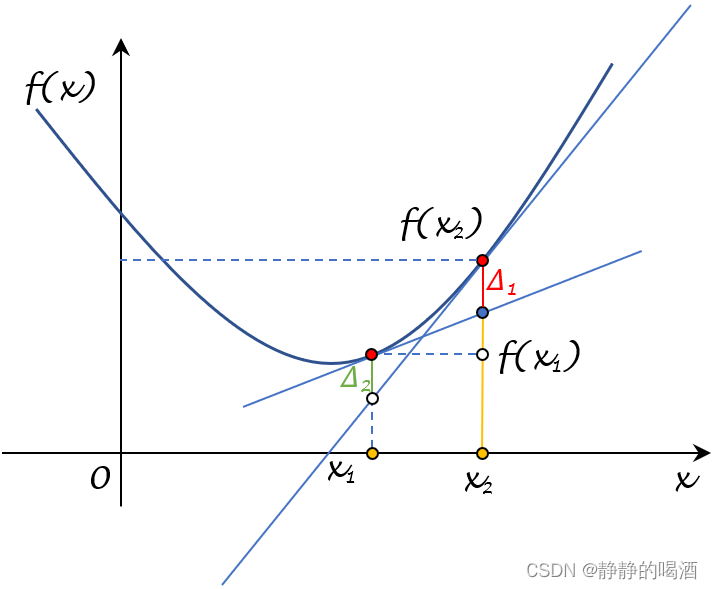
如果 Δ 1 \Delta_1 Δ1或者 Δ 2 \Delta_2 Δ2满足: Δ 1 ; Δ 2 ≥ 1 2 L ∣ ∣ ∇ f ( x 1 ) − ∇ f ( x 2 ) ∣ ∣ 2 \begin{aligned}\Delta_1;\Delta_2 \geq \frac{1}{2\mathcal L} ||\nabla f(x_1) - \nabla f(x_2)||^2\end{aligned} Δ1;Δ2≥2L1∣∣∇f(x1)−∇f(x2)∣∣2即可。
证明过程:
这里以 Δ 1 \Delta_1 Δ1为例,将 Δ 1 \Delta_1 Δ1展开,有:
Δ 1 = f ( x 2 ) − [ ∇ f ( x 1 ) ] T x 2 ⏟ 1 − { f ( x 1 ) − [ ∇ f ( x 1 ) ] T x 1 } ⏟ 2 \begin{aligned} \Delta_1 & = \underbrace{f(x_2) - [\nabla f(x_1)]^T x_2}_{1} - \underbrace{\left\{f(x_1) - [\nabla f(x_1)]^T x_1 \right\}}_{2} \end{aligned} Δ1=1 f(x2)−[∇f(x1)]Tx2−2 {f(x1)−[∇f(x1)]Tx1}
可以发现,上述的 1 , 2 1,2 1,2两个部分存在相同的格式。因此假设一个函数:
关于函数 H x 1 ( Z ) \mathcal H_{x_1}(\mathcal Z) Hx1(Z),其中 Z \mathcal Z Z是自变量,而内部的 x 1 x_1 x1被视作可变参数。
H x 1 ( Z ) = f ( Z ) − [ ∇ f ( x 1 ) ] T Z \mathcal H_{x_1}(\mathcal Z) = f(\mathcal Z) - [\nabla f(x_1)]^T \mathcal Z Hx1(Z)=f(Z)−[∇f(x1)]TZ
从而 Δ 1 \Delta_1 Δ1可表示为:
Δ 1 = H x 1 ( x 2 ) − H x 1 ( x 1 ) \Delta_1 = \mathcal H_{x_1}(x_2) - \mathcal H_{x_1}(x_1) Δ1=Hx1(x2)−Hx1(x1)
观察 H x 1 ( Z ) \mathcal H_{x_1}(\mathcal Z) Hx1(Z)函数,其中 f ( Z ) f(\mathcal Z) f(Z)是关于 Z \mathcal Z Z的凸函数;而 − [ ∇ f ( x 1 ) ] T Z -[\nabla f(x_1)]^T \mathcal Z −[∇f(x1)]TZ本质上是关于 Z \mathcal Z Z的一次函数,自然也是凸函数。根据保凸运算可知, H x 1 ( Z ) \mathcal H_{x_1}(\mathcal Z) Hx1(Z)一定是一个凸函数;并且由于 f ( Z ) f(\mathcal Z) f(Z)与 − [ ∇ f ( x 1 ) ] T Z -[\nabla f(x_1)]^T \mathcal Z −[∇f(x1)]TZ均在 Z \mathcal Z Z定义域内可微,因而 H x 1 ( Z ) \mathcal H_{x_1}(\mathcal Z) Hx1(Z)同样可微。因而 H x 1 ( Z ) \mathcal H_{x_1}(\mathcal Z) Hx1(Z)关于 Z \mathcal Z Z的梯度 ∇ H x 1 ( Z ) \nabla \mathcal H_{x_1}(\mathcal Z) ∇Hx1(Z)可表示为:
∇ H x 1 ( Z ) = ∇ f ( Z ) − ∇ f ( x 1 ) \begin{aligned}\nabla \mathcal H_{x_1}(\mathcal Z) = \nabla f(\mathcal Z) - \nabla f(x_1) \end{aligned} ∇Hx1(Z)=∇f(Z)−∇f(x1)
当 Z = x 1 \mathcal Z = x_1 Z=x1时,有: ∇ H x 1 ( x 1 ) = 0 \nabla \mathcal H_{x_1}(x_1) = 0 ∇Hx1(x1)=0。这意味着: Z = x 1 \mathcal Z = x_1 Z=x1是函数 H x 1 ( Z ) \mathcal H_{x_1}(\mathcal Z) Hx1(Z)的极值点。而又因为 H x 1 ( Z ) \mathcal H_{x_1}(\mathcal Z) Hx1(Z)的凸函数性质,因而该点一定是最小值点。记 H x 1 ( Z ) \mathcal H_{x_1}(\mathcal Z) Hx1(Z)的最小值结果为 H x 1 ∗ \mathcal H_{x_1}^* Hx1∗,从而可得:
H x 1 ∗ = H x 1 ( x 1 ) \mathcal H_{x_1}^* = \mathcal H_{x_1}(x_1) Hx1∗=Hx1(x1)
根据条件 2 2 2: G ( Z ) = L 2 Z T Z − f ( Z ) \begin{aligned}\mathcal G(\mathcal Z) = \frac{\mathcal L}{2} \mathcal Z^T \mathcal Z - f(\mathcal Z) \end{aligned} G(Z)=2LZTZ−f(Z)是凸函数,将 f ( Z ) = H x 1 ( Z ) + [ ∇ f ( x 1 ) ] T Z f(\mathcal Z) = \mathcal H_{x_1}(\mathcal Z) + [\nabla f(x_1)]^T \mathcal Z f(Z)=Hx1(Z)+[∇f(x1)]TZ代入到条件 2 2 2中有:
这里将变量符号 x x x替换成变量符号 Z \mathcal Z Z,便于下面的计算,并将 Z T Z \mathcal Z^T\mathcal Z ZTZ使用 ∣ ∣ Z ∣ ∣ 2 ||\mathcal Z||^2 ∣∣Z∣∣2替代。
G ( Z ) = L 2 ∣ ∣ Z ∣ ∣ 2 − f ( Z ) = L 2 ∣ ∣ Z ∣ ∣ 2 − H x 1 ( Z ) − [ ∇ f ( x 1 ) ] T Z ⇒ G ( Z ) + [ ∇ f ( x 1 ) ] T Z = L 2 ∣ ∣ Z ∣ ∣ 2 − H x 1 ( Z ) \begin{aligned} \mathcal G(\mathcal Z) & = \frac{\mathcal L}{2}||\mathcal Z||^2 - f(\mathcal Z) \\ & = \frac{\mathcal L}{2}||\mathcal Z||^2 - \mathcal H_{x_1}(\mathcal Z) - [\nabla f(x_1)]^T \mathcal Z \\ & \quad \\ \Rightarrow \mathcal G(\mathcal Z) + & [\nabla f(x_1)]^T \mathcal Z = \frac{\mathcal L}{2}||\mathcal Z||^2 - \mathcal H_{x_1}(\mathcal Z) \end{aligned} G(Z)⇒G(Z)+=2L∣∣Z∣∣2−f(Z)=2L∣∣Z∣∣2−Hx1(Z)−[∇f(x1)]TZ[∇f(x1)]TZ=2L∣∣Z∣∣2−Hx1(Z)
观察上式的等号左侧: G ( Z ) + [ ∇ f ( x 1 ) ] T Z \mathcal G(\mathcal Z) + [\nabla f(x_1)]^T \mathcal Z G(Z)+[∇f(x1)]TZ,同样可以如法炮制 H x 1 ( Z ) = f ( Z ) + [ ∇ f ( x 1 ) ] T Z \mathcal H_{x_1}(\mathcal Z) = f(\mathcal Z) + [\nabla f(x_1)]^T \mathcal Z Hx1(Z)=f(Z)+[∇f(x1)]TZ一样,定义一个符号 G x 1 ( Z ) \mathcal G_{x_1}(\mathcal Z) Gx1(Z),使得:
G x 1 ( Z ) = G ( Z ) + [ ∇ f ( x 1 ) ] T Z \mathcal G_{x_1}(\mathcal Z) = \mathcal G(\mathcal Z) + [\nabla f(x_1)]^T \mathcal Z Gx1(Z)=G(Z)+[∇f(x1)]TZ
观察 G x 1 ( Z ) \mathcal G_{x_1}(\mathcal Z) Gx1(Z)的相关性质:
- 关于第一项,根据条件 2 2 2描述: G ( Z ) \mathcal G(\mathcal Z) G(Z)自身是凸函数,可微;
- 关于第二项与 H x 1 ( Z ) \mathcal H_{x_1}(\mathcal Z) Hx1(Z)的第二项相同:关于 Z \mathcal Z Z的一次函数 [ ∇ f ( x 1 ) ] T Z [\nabla f(x_1)]^T \mathcal Z [∇f(x1)]TZ同样是凸函数,并在自身定义域内可微。
综上,依然可以根据保凸运算,关于函数 G x 1 ( Z ) \mathcal G_{x_1}(\mathcal Z) Gx1(Z)也是凸函数,并在定义域内可微。从而该函数的梯度 ∇ G x 1 ( Z ) \nabla \mathcal G_{x_1}(\mathcal Z) ∇Gx1(Z)表示如下:
∇ G x 1 ( Z ) = L 2 ⋅ 2 ⋅ Z − ∇ H x 1 ( Z ) = L ⋅ Z − ∇ H x 1 ( Z ) \begin{aligned} \nabla \mathcal G_{x_1}(\mathcal Z) & = \frac{\mathcal L}{2} \cdot 2 \cdot \mathcal Z - \nabla \mathcal H_{x_1}(\mathcal Z) \\ & = \mathcal L \cdot \mathcal Z - \nabla \mathcal H_{x_1}(\mathcal Z) \end{aligned} ∇Gx1(Z)=2L⋅2⋅Z−∇Hx1(Z)=L⋅Z−∇Hx1(Z)
根据 G x 1 ( Z ) \mathcal G_{x_1}(\mathcal Z) Gx1(Z)凸函数的性质,在 Z \mathcal Z Z定义域内取 z 1 ≤ z 2 , z 1 , z 2 ∈ R z_1 \leq z_2,z_1,z_2 \in \mathbb R z1≤z2,z1,z2∈R,必然有:
G x 1 ( z 2 ) ≥ G x 1 ( z 1 ) + [ ∇ G x 1 ( z 1 ) ] T ( z 2 − z 1 ) \mathcal G_{x_1}(z_2) \geq \mathcal G_{x_1}(z_1) + \left[\nabla \mathcal G_{x_1}(z_1)\right]^T(z_2 - z_1) Gx1(z2)≥Gx1(z1)+[∇Gx1(z1)]T(z2−z1)
从上述图像中观察更加直观。也就是说: Δ 1 ≥ 0 \Delta_1 \geq 0 Δ1≥0恒成立。将上述 G x 1 ( Z ) = L 2 ∣ ∣ Z ∣ ∣ 2 − H x 1 ( Z ) \begin{aligned}\mathcal G_{x_1}(\mathcal Z) = \frac{\mathcal L}{2}||\mathcal Z||^2 - \mathcal H_{x_1}(\mathcal Z)\end{aligned} Gx1(Z)=2L∣∣Z∣∣2−Hx1(Z)代入,有:
L 2 ∣ ∣ z 2 ∣ ∣ 2 − H x 1 ( z 2 ) ⏟ G x 1 ( z 2 ) ≥ L 2 ∣ ∣ z 1 ∣ ∣ 2 − H x 1 ( z 1 ) ⏟ G x 1 ( x 1 ) + [ L ⋅ z 1 − ∇ H x 1 ( z 1 ) ] T ⏟ [ G x 1 ( z 1 ) ] T ⋅ ( z 2 − z 1 ) \underbrace{\frac{\mathcal L}{2} ||z_2||^2 - \mathcal H_{x_1}(z_2)}_{\mathcal G_{x_1}(z_2)} \geq \underbrace{\frac{\mathcal L}{2}||z_1||^2 - \mathcal H_{x_1}(z_1)}_{\mathcal G_{x_1}(x_1)} + \underbrace{[\mathcal L \cdot z_1 - \nabla \mathcal H_{x_1}(z_1)]^T}_{[\mathcal G_{x_1}(z_1)]^T} \cdot (z_2 - z_1) Gx1(z2) 2L∣∣z2∣∣2−Hx1(z2)≥Gx1(x1) 2L∣∣z1∣∣2−Hx1(z1)+[Gx1(z1)]T [L⋅z1−∇Hx1(z1)]T⋅(z2−z1)
至此,描述 G x 1 ( Z ) \mathcal G_{x_1}(\mathcal Z) Gx1(Z)凸函数性质的式子全部由 H x 1 ( Z ) \mathcal H_{x_1}(\mathcal Z) Hx1(Z)进行代替。经过整理,有:
对比一下二次上界引理,它们确实比较相似,但并不是。因为 L 2 ∣ ∣ z 2 ∣ ∣ 2 − L 2 ∣ ∣ z 1 ∣ ∣ 2 \begin{aligned}\frac{\mathcal L}{2}||z_2||^2 - \frac{\mathcal L}{2}||z_1||^2\end{aligned} 2L∣∣z2∣∣2−2L∣∣z1∣∣2与 L 2 ∣ ∣ z 2 − z 1 ∣ ∣ 2 \begin{aligned}\frac{\mathcal L}{2}||z_2 - z_1||^2\end{aligned} 2L∣∣z2−z1∣∣2绝大多数情况不相等。
H x 1 ( z 2 ) ≤ L 2 ∣ ∣ z 2 ∣ ∣ 2 − L 2 ∣ ∣ z 1 ∣ ∣ 2 + H x 1 ( z 1 ) + [ ∇ H x 1 ( z 1 ) − L ⋅ z 1 ] T ( z 2 − z 1 ) \mathcal H_{x_1}(z_2) \leq \frac{\mathcal L}{2}||z_2||^2 - \frac{\mathcal L}{2} ||z_1||^2 + \mathcal H_{x_1}(z_1) + \left[\nabla \mathcal H_{x_1}(z_1) - \mathcal L \cdot z_1\right]^T(z_2 - z_1) Hx1(z2)≤2L∣∣z2∣∣2−2L∣∣z1∣∣2+Hx1(z1)+[∇Hx1(z1)−L⋅z1]T(z2−z1)
但该式子并不影响我们使用二次上界引理中的操作:将 z 1 z_1 z1视作上一次迭代产生的数值解,因而 z 1 z_1 z1是已知项,从而不等式右侧是关于 z 2 z_2 z2的函数,记作 ϕ ( z 2 ) \phi(z_2) ϕ(z2):
H x 1 ( z 2 ) ≤ ϕ ( z 2 ) ≜ L 2 ∣ ∣ z 2 ∣ ∣ 2 − L 2 ∣ ∣ z 1 ∣ ∣ 2 + H x 1 ( z 1 ) + [ ∇ H x 1 ( z 1 ) − L ⋅ z 1 ] T ( z 2 − z 1 ) \mathcal H_{x_1}(z_2) \leq \phi(z_2) \triangleq \frac{\mathcal L}{2}||z_2||^2 - \frac{\mathcal L}{2} ||z_1||^2 + \mathcal H_{x_1}(z_1) + \left[\nabla \mathcal H_{x_1}(z_1) - \mathcal L \cdot z_1\right]^T(z_2 - z_1) Hx1(z2)≤ϕ(z2)≜2L∣∣z2∣∣2−2L∣∣z1∣∣2+Hx1(z1)+[∇Hx1(z1)−L⋅z1]T(z2−z1)
再次观察 ϕ ( z 2 ) \phi(z_2) ϕ(z2)中与 z 2 z_2 z2相关的项(其中仅与 z 1 z_1 z1相关的项被视作常数):
- L 2 ∣ ∣ z 2 ∣ ∣ 2 \begin{aligned}\frac{\mathcal L}{2}||z_2||^2\end{aligned} 2L∣∣z2∣∣2是关于 z 2 z_2 z2的二次项,是凸函数;且二次项系数 L 2 ≥ 0 \begin{aligned}\frac{\mathcal L}{2} \geq 0\end{aligned} 2L≥0,必然存在最小值;
- [ ∇ H x 1 ( z 1 ) − L ⋅ z 1 ] T ( z 2 − z 1 ) \left[\nabla \mathcal H_{x_1}(z_1) - \mathcal L \cdot z_1\right]^T(z_2 - z_1) [∇Hx1(z1)−L⋅z1]T(z2−z1)是关于 z 1 z_1 z1的一次函数,同样是凸函数。
最终通过保凸运算,能够确定 ϕ ( z 2 ) \phi(z_2) ϕ(z2)是一个凸二次函数。由于 H x 1 ( z 2 ) ≤ ϕ ( z 2 ) \mathcal H_{x_1}(z_2) \leq \phi(z_2) Hx1(z2)≤ϕ(z2),必然也小于 ϕ ( z 2 ) \phi(z_2) ϕ(z2)的最小值,也就是下界 inf { ϕ ( z 2 ) } = min ϕ ( z 2 ) \inf \{\phi(z_2)\} = \mathop{\min} \phi(z_2) inf{ϕ(z2)}=minϕ(z2):
H x 1 ( z 2 ) ≤ inf { ϕ ( z 2 ) } \mathcal H_{x_1}(z_2) \leq \inf \{\phi(z_2)\} Hx1(z2)≤inf{ϕ(z2)}
下面关于 inf { ϕ ( z 2 ) } \inf\{\phi(z_2)\} inf{ϕ(z2)}进行求解:
- 求解梯度 ∇ ϕ ( z 2 ) \nabla \phi(z_2) ∇ϕ(z2):
∇ ϕ ( z 2 ) = L ⋅ z 2 + ∇ H x 1 ( z 1 ) − L ⋅ z 1 \nabla \phi(z_2) = \mathcal L \cdot z_2 + \nabla \mathcal H_{x_1}(z_1) - \mathcal L \cdot z_1 ∇ϕ(z2)=L⋅z2+∇Hx1(z1)−L⋅z1 - 令 ∇ ϕ ( z 2 ) ≜ 0 \nabla \phi(z_2) \triangleq 0 ∇ϕ(z2)≜0,有:
也就是说:ϕ ( z 2 ; m i n ) = min ϕ ( z 2 ) \phi(z_{2;min}) = \min \phi(z_2) ϕ(z2;min)=minϕ(z2)。
z 2 ; m i n = z 1 − ∇ H x 1 ( z 1 ) L z_{2;min} =z_1 - \frac{\nabla \mathcal H_{x_1}(z_1)}{\mathcal L} z2;min=z1−L∇Hx1(z1) - 将 z 2 ; m i n z_{2;min} z2;min带回原式,得到 min ϕ ( z 2 ) \min \phi(z_2) minϕ(z2)有:
ϕ ( z 2 ; m i n ) = L 2 ∣ ∣ L ⋅ z 1 − ∇ H x 1 ( z 1 ) L ∣ ∣ 2 − L 2 ∣ ∣ z 1 ∣ ∣ 2 + H x 1 ( z 1 ) + [ ∇ H x 1 ( z 1 ) − L ⋅ z 1 ] T [ − ∇ H x 1 ( z 1 ) L ] \phi(z_{2;min}) = \frac{\mathcal L}{2} ||\frac{\mathcal L\cdot z_1 - \nabla \mathcal H_{x_1}(z_1)}{\mathcal L}||^2 - \frac{\mathcal L}{2}||z_1||^2 + \mathcal H_{x_1}(z_1) + [\nabla \mathcal H_{x_1}(z_1) - \mathcal L \cdot z_1]^T\left[- \frac{\nabla \mathcal H_{x_1}(z_1)}{\mathcal L}\right] ϕ(z2;min)=2L∣∣LL⋅z1−∇Hx1(z1)∣∣2−2L∣∣z1∣∣2+Hx1(z1)+[∇Hx1(z1)−L⋅z1]T[−L∇Hx1(z1)] - 很明显,只剩下了已知项 z 1 z_1 z1。整理有:
提出公因式1 2 L [ L ⋅ z 1 − ∇ H x 1 ( z 1 ) ] \begin{aligned}\frac{1}{2\mathcal L}[\mathcal L \cdot z_1 - \nabla \mathcal H_{x_1}(z_1)]\end{aligned} 2L1[L⋅z1−∇Hx1(z1)]使用乘法分配律~
ϕ ( z 2 ; m i n ) = 1 2 L ∣ ∣ L ⋅ z 1 − ∇ H x 1 ( z 1 ) ∣ ∣ 2 − L 2 ∣ ∣ z 1 ∣ ∣ 2 + H x 1 ( z 1 ) + 1 L [ L ⋅ z 1 − ∇ H x 1 ( z 1 ) ] T ∇ H x 1 ( z 1 ) = 1 2 L [ L ⋅ z 1 − ∇ H x 1 ( z 1 ) ] T { L ⋅ z 1 − ∇ H x 1 ( z 1 ) + 2 ∇ H x 1 ( z 1 ) } + h x 1 ( z 1 ) − L 2 ∣ ∣ z 1 ∣ ∣ 2 = 1 2 L [ L ⋅ z 1 − ∇ H x 1 ( z 1 ) ] T { L ⋅ z 1 + ∇ H x 1 ( z 1 ) } ⏟ 分配律 + h x 1 ( z 1 ) − L 2 ∣ ∣ z 1 ∣ ∣ 2 = 1 2 L [ L 2 ⋅ ∣ ∣ z 1 ∣ ∣ 2 − ∣ ∣ ∇ H x 1 ( z 1 ) ∣ ∣ 2 ] + H x 1 ( z 1 ) − L 2 ∣ ∣ z 1 ∣ ∣ 2 = H x 1 ( z 1 ) − 1 2 L ∣ ∣ ∇ H x 1 ( z 1 ) ∣ ∣ 2 \begin{aligned} \phi(z_{2;min}) & = \frac{1}{2\mathcal L}||\mathcal L \cdot z_1 - \nabla \mathcal H_{x_1}(z_1)||^2 - \frac{\mathcal L}{2}||z_1||^2 + \mathcal H_{x_1}(z_1) + \frac{1}{\mathcal L} [\mathcal L \cdot z_1 - \nabla \mathcal H_{x_1}(z_1)]^T \nabla \mathcal H_{x_1}(z_1) \\ & = \frac{1}{2\mathcal L} [\mathcal L \cdot z_1 - \nabla \mathcal H_{x_1}(z_1)]^T \left\{\mathcal L \cdot z_1 - \nabla \mathcal H_{x_1}(z_1) + 2 \nabla \mathcal H_{x_1}(z_1)\right\} + h_{x_1}(z_1) - \frac{\mathcal L}{2}||z_1||^2 \\ & = \frac{1}{2\mathcal L} \underbrace{[\mathcal L \cdot z_1 - \nabla \mathcal H_{x_1}(z_1)]^T \left\{\mathcal L \cdot z_1 + \nabla \mathcal H_{x_1}(z_1) \right\}}_{分配律} + h_{x_1}(z_1) - \frac{\mathcal L}{2}||z_1||^2 \\ & = \frac{1}{2\mathcal L} \left[\mathcal L^2 \cdot ||z_1||^2 - ||\nabla \mathcal H_{x_1}(z_1)||^2\right] + \mathcal H_{x_1}(z_1) - \frac{\mathcal L}{2}||z_1||^2 \\ & = \mathcal H_{x_1}(z_1) - \frac{1}{2\mathcal L}||\nabla \mathcal H_{x_1}(z_1)||^2 \end{aligned} ϕ(z2;min)=2L1∣∣L⋅z1−∇Hx1(z1)∣∣2−2L∣∣z1∣∣2+Hx1(z1)+L1[L⋅z1−∇Hx1(z1)]T∇Hx1(z1)=2L1[L⋅z1−∇Hx1(z1)]T{L⋅z1−∇Hx1(z1)+2∇Hx1(z1)}+hx1(z1)−2L∣∣z1∣∣2=2L1分配律 [L⋅z1−∇Hx1(z1)]T{L⋅z1+∇Hx1(z1)}+hx1(z1)−2L∣∣z1∣∣2=2L1[L2⋅∣∣z1∣∣2−∣∣∇Hx1(z1)∣∣2]+Hx1(z1)−2L∣∣z1∣∣2=Hx1(z1)−2L1∣∣∇Hx1(z1)∣∣2
至此,我们找到了关于 H x 1 ( z 2 ) \mathcal H_{x_1}(z_2) Hx1(z2)的二次上界:
H x 1 ( z 2 ) ≤ H x 1 ( z 1 ) − 1 2 L ∣ ∣ ∇ H x 1 ( z 1 ) ∣ ∣ 2 \mathcal H_{x_1}(z_2) \leq \mathcal H_{x_1}(z_1) - \frac{1}{2\mathcal L}||\nabla \mathcal H_{x_1}(z_1)||^2 Hx1(z2)≤Hx1(z1)−2L1∣∣∇Hx1(z1)∣∣2
在 H x 1 ( ⋅ ) \mathcal H_{x_1}(\cdot) Hx1(⋅)函数的收敛过程中,其最小值 H x 1 ∗ \mathcal H_{x_1}^* Hx1∗必然有:
通过数值解只能无限接近最小值。
H x 1 ∗ ≤ H x 1 ( z 2 ) ≤ H x 1 ( z 1 ) − 1 2 L ∣ ∣ ∇ H x 1 ( z 1 ) ∣ ∣ 2 \mathcal H_{x_1}^* \leq \mathcal H_{x_1}(z_2) \leq \mathcal H_{x_1}(z_1) - \frac{1}{2\mathcal L}||\nabla \mathcal H_{x_1}(z_1)||^2 Hx1∗≤Hx1(z2)≤Hx1(z1)−2L1∣∣∇Hx1(z1)∣∣2
因为 H x 1 ( ⋅ ) \mathcal H_{x_1}(\cdot) Hx1(⋅)函数在 x 1 x_1 x1处取得最小值: H x 1 ( x 1 ) = H x 1 ∗ \mathcal H_{x_1}(x_1) = \mathcal H_{x_1}^* Hx1(x1)=Hx1∗,并且 z 1 z_1 z1与 x 1 x_1 x1定义域相同,不妨设: z 1 = x 2 z_1 = x_2 z1=x2,有:
H x 1 ( x 1 ) ≤ H x 1 ( x 2 ) − 1 2 L ∣ ∣ ∇ H x 1 ( x 2 ) ∣ ∣ 2 ⇒ H x 1 ( x 2 ) − H x 1 ( x 1 ) ≥ 1 2 L ∣ ∣ ∇ H x 1 ( x 2 ) ∣ ∣ 2 \begin{aligned} & \mathcal H_{x_1}(x_1) \leq \mathcal H_{x_1}(x_2) - \frac{1}{2\mathcal L}||\nabla \mathcal H_{x_1}(x_2)||^2 \\ \Rightarrow & \mathcal H_{x_1}(x_2) - \mathcal H_{x_1}(x_1) \geq \frac{1}{2\mathcal L}||\nabla \mathcal H_{x_1}(x_2)||^2 \end{aligned} ⇒Hx1(x1)≤Hx1(x2)−2L1∣∣∇Hx1(x2)∣∣2Hx1(x2)−Hx1(x1)≥2L1∣∣∇Hx1(x2)∣∣2
由于 Δ 1 = H x 1 ( x 2 ) − H x 1 ( x 1 ) \Delta_1 = \mathcal H_{x_1}(x_2) - \mathcal H_{x_1}(x_1) Δ1=Hx1(x2)−Hx1(x1),因而最终有:
将 ∇ H x 1 ( Z = x 2 ) = ∇ f ( x 2 ) − ∇ f ( x 1 ) \nabla \mathcal H_{x_1}(\mathcal Z = x_2) = \nabla f(x_2) - \nabla f(x_1) ∇Hx1(Z=x2)=∇f(x2)−∇f(x1)代入:
Δ 1 ≥ 1 2 L ∣ ∣ ∇ H x 1 ( x 2 ) ∣ ∣ 2 = 1 2 L ∣ ∣ ∇ f ( x 2 ) − ∇ f ( x 1 ) ∣ ∣ 2 = 1 2 L ∣ ∣ ∇ f ( x 1 ) − ∇ f ( x 2 ) ∣ ∣ 2 \begin{aligned} \Delta_1 & \geq \frac{1}{2\mathcal L}||\nabla \mathcal H_{x_1}(x_2)||^2 \\ & = \frac{1}{2\mathcal L} ||\nabla f(x_2) - \nabla f(x_1)||^2 \\ & = \frac{1}{2\mathcal L} ||\nabla f(x_1) - \nabla f(x_2)||^2 \end{aligned} Δ1≥2L1∣∣∇Hx1(x2)∣∣2=2L1∣∣∇f(x2)−∇f(x1)∣∣2=2L1∣∣∇f(x1)−∇f(x2)∣∣2
当然,这仅仅证明了一半,我们同样需要针对 Δ 2 \Delta_2 Δ2执行上述流程:
和上述流程完全相同,只不过可变参数由 x 1 x_1 x1变成了 x 2 x_2 x2,这里不再赘述。
Δ 2 = [ f ( x 1 ) − f ( x 2 ) ] − { [ ∇ f ( x 2 ) ] T x 1 − [ ∇ f ( x 2 ) ] T x 2 } = f ( x 1 ) − [ ∇ f ( x 2 ) ] T x 1 ⏟ 1 − { f ( x 2 ) − [ ∇ f ( x 2 ) ] T x 2 } ⏟ 2 = H x 2 ( x 1 ) − H x 2 ( x 2 ) \begin{aligned} \Delta_2 & = [f(x_1) - f(x_2)] - \left\{[\nabla f(x_2)]^T x_1 - [\nabla f(x_2)]^T x_2 \right\} \\ & = \underbrace{f(x_1) - [\nabla f(x_2)]^T x_1}_{1} - \underbrace{\{f(x_2) - [\nabla f(x_2)]^T x_2\}}_{2} \\ & = \mathcal H_{x_2}(x_1) - \mathcal H_{x_2}(x_2) \end{aligned} Δ2=[f(x1)−f(x2)]−{[∇f(x2)]Tx1−[∇f(x2)]Tx2}=1 f(x1)−[∇f(x2)]Tx1−2 {f(x2)−[∇f(x2)]Tx2}=Hx2(x1)−Hx2(x2)
最终也可以得到一个类似结果:
Δ 2 ≥ 1 2 L ∣ ∣ ∇ f ( x 1 ) − ∇ f ( x 2 ) ∣ ∣ 2 \Delta_2 \geq \frac{1}{2\mathcal L} ||\nabla f(x_1) - \nabla f(x_2)||^2 Δ2≥2L1∣∣∇f(x1)−∇f(x2)∣∣2
从而最终可得:
Δ 1 + Δ 2 ≥ 2 ⋅ 1 2 L ∣ ∣ ∇ f ( x 1 ) − ∇ f ( x 2 ) ∣ ∣ 2 = 1 L ∣ ∣ ∇ f ( x 1 ) − ∇ f ( x 2 ) ∣ ∣ 2 \begin{aligned} \Delta_1 + \Delta_2 & \geq 2 \cdot \frac{1}{2\mathcal L}||\nabla f(x_1) - \nabla f(x_2)||^2 \\ & = \frac{1}{\mathcal L} ||\nabla f(x_1) - \nabla f(x_2)||^2 \end{aligned} Δ1+Δ2≥2⋅2L1∣∣∇f(x1)−∇f(x2)∣∣2=L1∣∣∇f(x1)−∇f(x2)∣∣2
即:
[ ∇ f ( x 1 ) − ∇ f ( x 2 ) ] T ( x 1 − x 2 ) ≥ 1 L ∣ ∣ ∇ f ( x 1 ) − ∇ f ( x 2 ) ∣ ∣ 2 [\nabla f(x_1) - \nabla f(x_2)]^T(x_1 - x_2) \geq \frac{1}{\mathcal L} ||\nabla f(x_1) - \nabla f(x_2)||^2 [∇f(x1)−∇f(x2)]T(x1−x2)≥L1∣∣∇f(x1)−∇f(x2)∣∣2
即梯度函数 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)具备余强制性,证毕。
相关参考:
【优化算法】梯度下降法-白老爹定理(上)
【优化算法】梯度下降法-白老爹定理(下)
相关文章:

机器学习笔记之优化算法(十五)Baillon Haddad Theorem简单认识
机器学习笔记之优化算法——Baillon Haddad Theorem简单认识 引言 Baillon Haddad Theorem \text{Baillon Haddad Theorem} Baillon Haddad Theorem简单认识证明过程证明:条件 1 ⇒ 1 \Rightarrow 1⇒ 条件 2 2 2证明:条件 3 ⇒ 3 \Rightarrow 3⇒条件 1…...

HighTec工程用命令行编译
当工程中含有太多模型生成的代码的时候,如果修改了一部分代码,HighTec自带的编译器编译时间会非常的慢,有的需要半个小时甚至一个小时,这是因为每次修改之后HighTec都会从头重新检索更新,太浪费时间了,于是…...
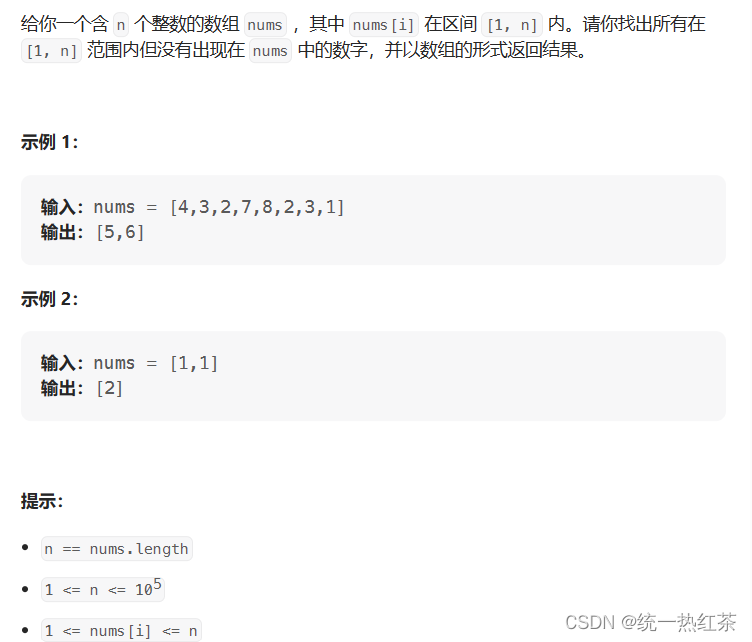
【C语言】每日一题(找到所有数组中消失的数字)
找到所有数组中消失的数字,链接奉上。 这里简单说一下,因为还没有接触到动态内存,数据结构,所以知识有限,也是尽力而为,结合题库的评论区找到了适合我的解法,以后有机会,会补上各种…...
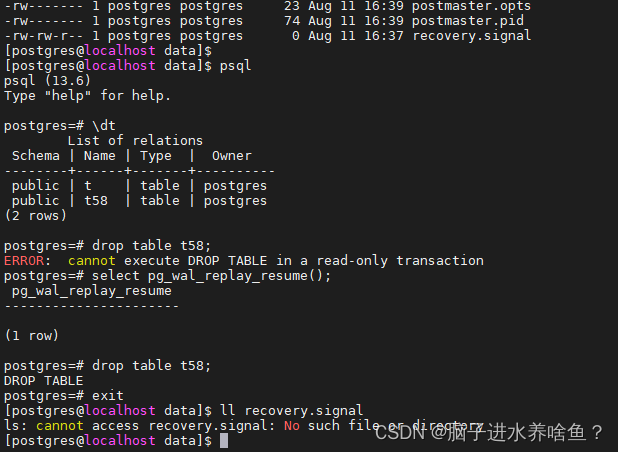
PostgreSql 备份恢复
一、概述 数据库备份一般可分为物理备份和逻辑备份,其中物理备份又可分为物理冷备和物理热备,下面就各种备份方式进行详细说明(一般情况下,生产环境采取的定时物理热备逻辑备份的方式,均是以下述方式为基础进一步研发编…...

鲲鹏916/920处理器性能比较
CPUKunpeng916Kunpeng920指令集Cotex-A75TaiShan-V110主频2.4GHz2.6GHz/3.0GHz核数3224/32/48/64CacheL1: 48 KB instruction cache and 32 KB data cache L2: 256 KB private per core L3: 32 MB L1: 64 KB instruction cache and 64 KB data cache L2: 512 KB private per co…...
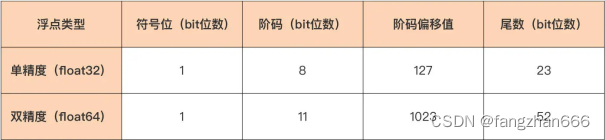
《Go 语言第一课》课程学习笔记(八)
基本数据类型 Go 原生支持的数值类型有哪些? Go 语言的类型大体可分为基本数据类型、复合数据类型和接口类型这三种。 其中,我们日常 Go 编码中使用最多的就是基本数据类型,而基本数据类型中使用占比最大的又是数值类型。 整型 Go 语言的…...

管理类联考——逻辑——真题篇——按知识分类——汇总篇——一、形式逻辑——联选言
文章目录 第五节 联言+选言-摩根定理-非(A或B)=非A且非B,非(A且B)=非A或非B真题(2013-49)-联言+选言-摩根定理-非(A或B)=非A且非B,非(A且B)=非A或非B真题(2012-33)-联言+选言-摩根定理-非(A或B)=非A且非B,非(A且B)=非A或非B真题(2014-42)-联言+选言-摩根定理-非(A或B…...
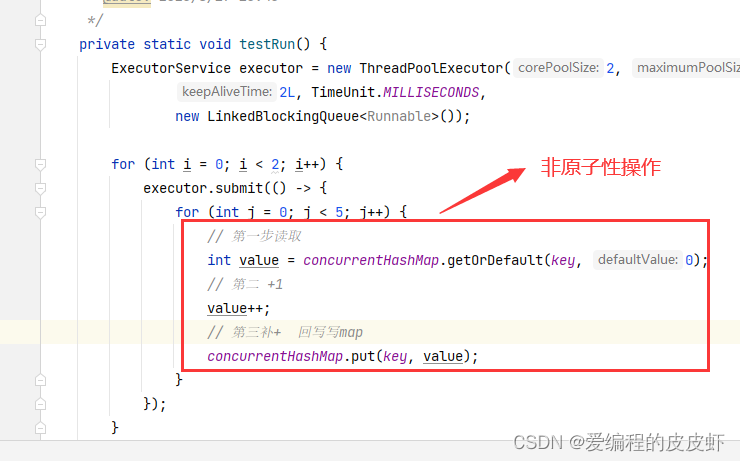
CAS 一些隐藏的知识,您了解吗
目录 ConcurrentHashMap 一定是线程安全的吗 CAS 机制的注意事项 使用java 并行流 ,您要留意了 ConcurrentHashMap 在JDK1.8中ConcurrentHashMap 内部使用的是数组加链表加红黑树的结构,通过CASvolatile或synchronized的方式来保证线程安全的,这些原理…...

ChatGPT逐句逐句地解释代码并分析复杂度的提示词prompt
前提安装chrome 插件 AI Prompt Genius, 请参考 3 个 ChatGPT 插件您需要立即下载 你是首席软件工程师。请解释这段代码:{{code}} 添加注释并重写代码,用注释解释每一行代码的作用。最后分析复杂度。快捷键 / 选择 Explain Code 输入代码提…...

【Lua语法】算术、条件、逻辑、位、三目运算符
1.算术运算符 加减乘除取余: - * / % Lua中独有的:幂运算 ^ 注意: 1.Lua中没有自增自减(、–),也没有复合运算符(、-) 2.Lua中字符串可以进行算术运算符操作,会自动转成number 如:“10.3” 1 结果为11.3…...
Cygwin 配置C/C++编译环境以及如何编译项目
文章目录 一、安装C、C编译环境需要的包1. 选择gcc-core、gcc-g2. 选择gdb3. 选择mingw64下的gcc-core、gcc-g4. 选择make5. 选择cmake6. 确认更改7. 查看包安装状态 二、C、C 项目编译示例step1:解压缩sed-4.9.tar.gzstep2:执行./configure生成Makefile…...

回归预测 | MATLAB实现FA-BP萤火虫算法优化BP神经网络多输入单输出回归预测(多指标,多图)
回归预测 | MATLAB实现FA-BP萤火虫算法优化BP神经网络多输入单输出回归预测(多指标,多图) 目录 回归预测 | MATLAB实现FA-BP萤火虫算法优化BP神经网络多输入单输出回归预测(多指标,多图)效果一览基本介绍程…...
【100天精通python】Day39:GUI界面编程_PyQt 从入门到实战(下)_图形绘制和动画效果,数据可视化,刷新交互
目录 专栏导读 6 图形绘制与动画效果 6.1 绘制基本图形、文本和图片 6.2 实现动画效果和过渡效果 7 数据可视化 7.1 使用 Matplotlib绘制图表 7.2 使用PyQtGraph绘制图表 7.3 数据的实时刷新和交互操作 7.3.1 数据的实时刷新 7.3.2 交互操作 7.4 自定义数据可视化…...
Java课题笔记~ Ajax
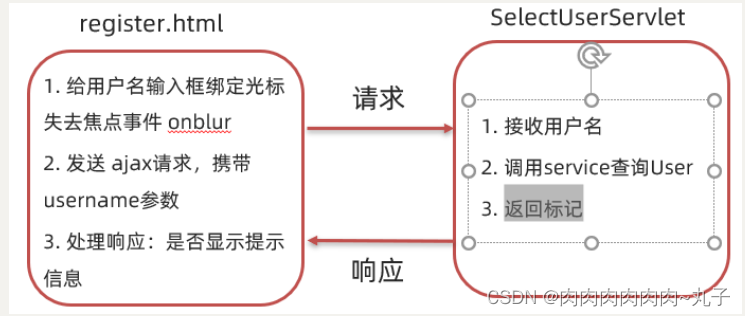
1.1 概述 AJAX (Asynchronous JavaScript And XML):异步的 JavaScript 和 XML。 我们先来说概念中的 JavaScript 和 XML,JavaScript 表明该技术和前端相关;XML 是指以此进行数据交换。 1.1.1 作用 AJAX 作用有以下两方面: 与服…...
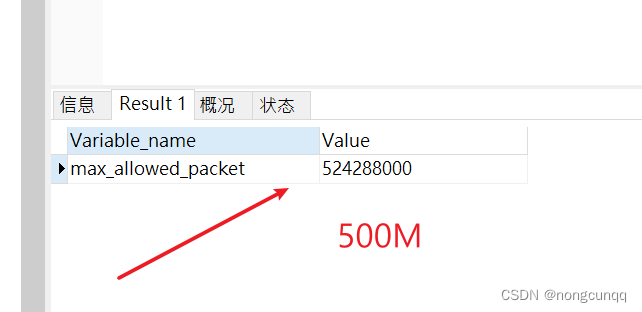
调整mysql 最大传输数据 max_allowed_packet=500M
查看 -- show VARIABLES like %max_allowed_packet%; -- set global max_allowed_packet 1024*1024*64;-- show variables like %timeout%; -- show global status like com_kill; show global variables like max_allowed_packet; -- set global max_allowed_packet1024*102…...
【工具】 删除Chrome安装的“创建快捷方式”
创建Chrome的快捷方式,可以放在桌面,想用时双击就可以打开网页,比书签(brookmark)结构化管理更方便。 但是,安装一时爽,卸载有问题。 如果用 windows 控制面板\所有控制面板项\程序和功能 卸载…...
windows上的docker自动化部署到服务器脚本
1、mvn install后,双击这个bat,实现docker build后上传到124服务器,并且重启124服务器 **echo offsetlocal:: 定义镜像名称和版本变量 set IMAGE_NAMEweb set IMAGE_VERSION1.3.1:: 清理本地文件 echo Cleaning up... del service-%IMAGE_N…...

VoxWeekly|The Sandbox 生态周报|20230814
欢迎来到由 The Sandbox 发布的《VoxWeekly》。我们会在每周发布,对上一周 The Sandbox 生态系统所发生的事情进行总结。 如果你喜欢我们内容,欢迎与朋友和家人分享。请订阅我们的 Medium 、关注我们的 Twitter,并加入 Discord 社区…...
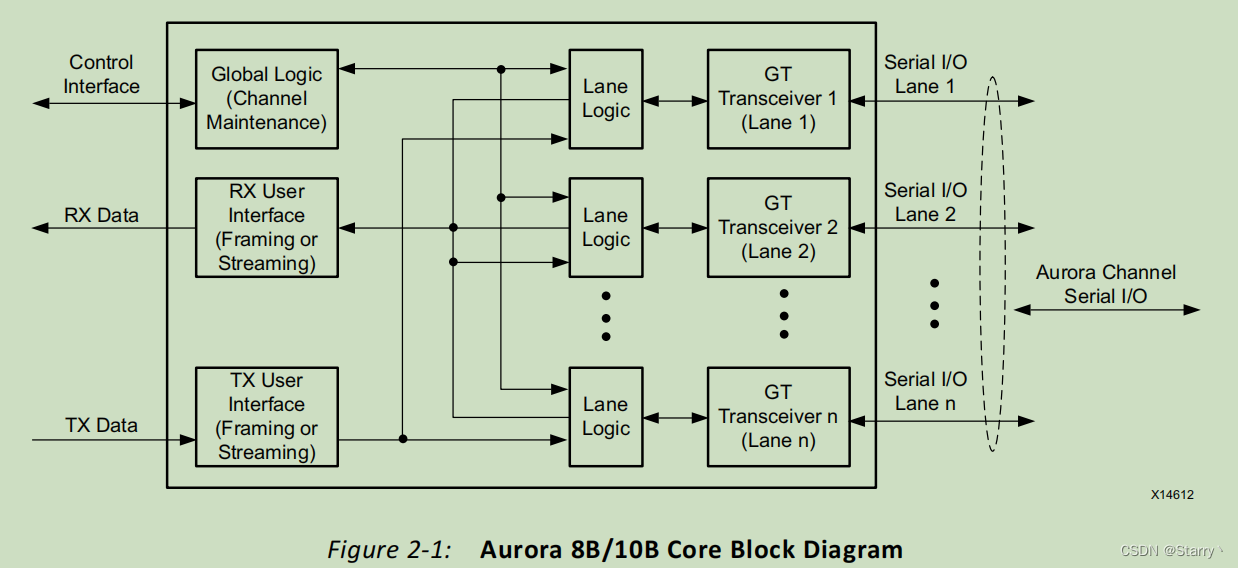
Aurora 8B/10B
目录 1. Overview2. Feature List2. Block Diagram3. Ports Description3.1. User InterfaceFraming InterfaceStreaming InterfaceUser Flow Control(UFC)Native Flow Control(NFC) 3.2. Status and Control Ports3.3. Transceiv…...

如何关闭“若要接收后续google chrome更新,您需使用windows10或更高版本”
Windows Registry Editor Version 5.00[HKEY_CURRENT_USER\Software\Policies\Google\Chrome] "SuppressUnsupportedOSWarning"dword:00000001 如何关闭“若要接收后续 google chrome 更新,您需使用 windows 10 或更高版本” - 知乎...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

Neko虚拟浏览器远程协作方案:Docker+内网穿透技术部署实践
前言:本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中,跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南,你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案,并结合内网…...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...
