Tableau画图
目录
蝴蝶图
四象图
排序图
盒型图/散点图
圆环图
火柴图
直方图
瀑布图
地理图
面积图
树地图
面积图
条形图
词云图
双轴图
填充地图
tableau2023.2
须知

蝴蝶图

拉好数据之后

创建新字段正负销售额,并拖入第一个颜色标记卡

四象图

智能推荐 散点图-> 分析 -》参考线 -》创建新参数 -》自定义参数名 -》修改值


单独设置x/y轴,可以单击x线或y线 右键编辑
排序图

拉好数据之后(重复拉两个销售额)一个设置为线 另一个为圆
第二个销售额右键点击双轴
再将类别(想放在一张表里对比的字段)拉入颜色
盒型图/散点图

圆环图

先拉好数据之后,建两个饼图(a选饼图)
上方的计数订单右键-》快速表计算 -》 合计百分比(两个字段的饼图操作一样)
将下面一个饼图的颜色换为白色 -》 标签全部去除
再右键行的计数字段,点击双轴

蓝色区域右键编辑轴 -》 范围改为固定 -》固定结束值自己调
让下方的白色饼图覆盖上方造成中间空白,做成圆环图
火柴图

本质是条形图+圆形
拉好数据之后,度量值重复拉两个,一个条形图 另一个圆
,将条形图大小拉小一点,其中一个的标记关掉
直方图

瀑布图

拉好数据之后点击智能推荐条形图,点击上方的转置
点击a -》甘特条形图
再创建一个度量字段改为负值

将这个新创建字段拉入标记里的大小
再将行列的值右键 点击快速表计算 -》累计汇总
地理图

点击智能推荐地理图 /可以点击上方地图更换背景
树地图
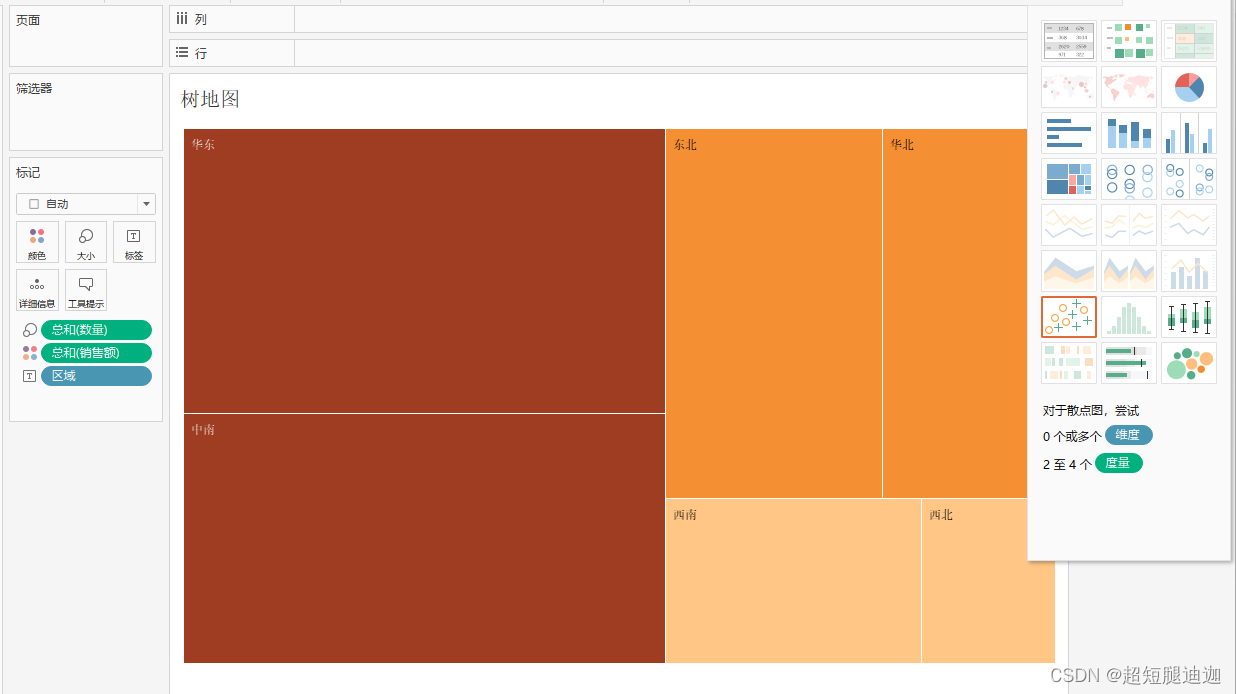
拉好需要数据,智能推荐树状图
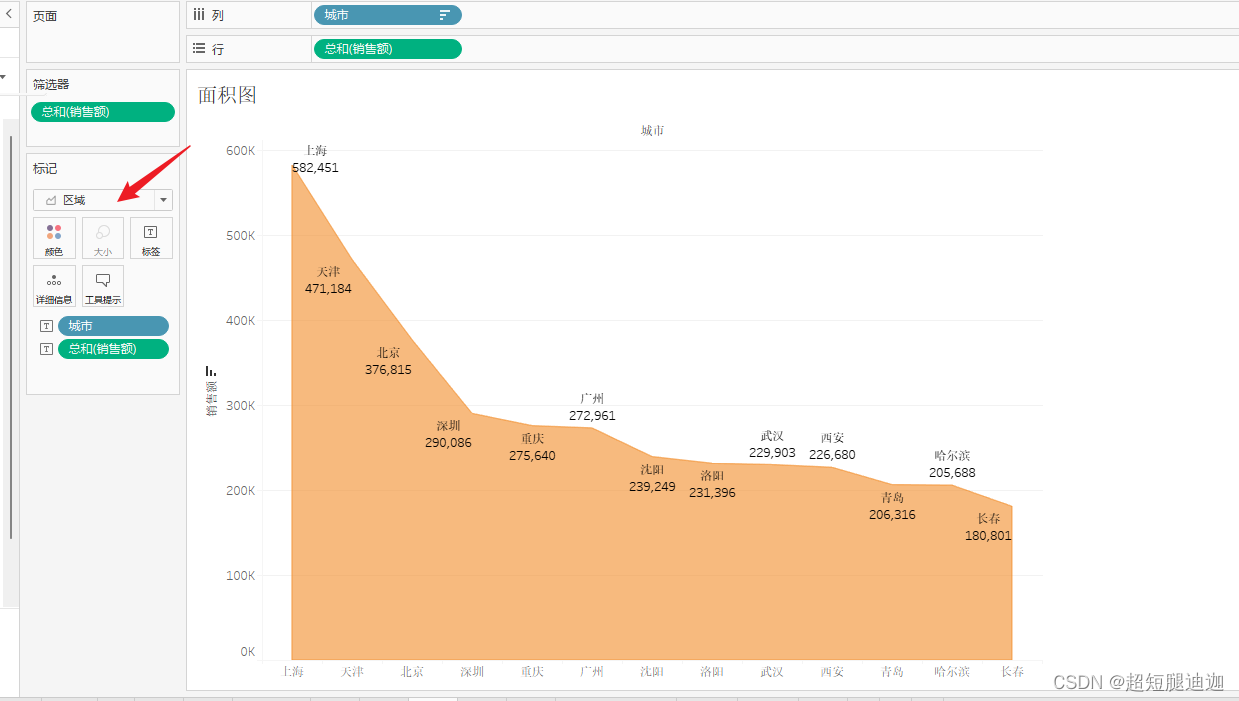
面积图
a改成区域
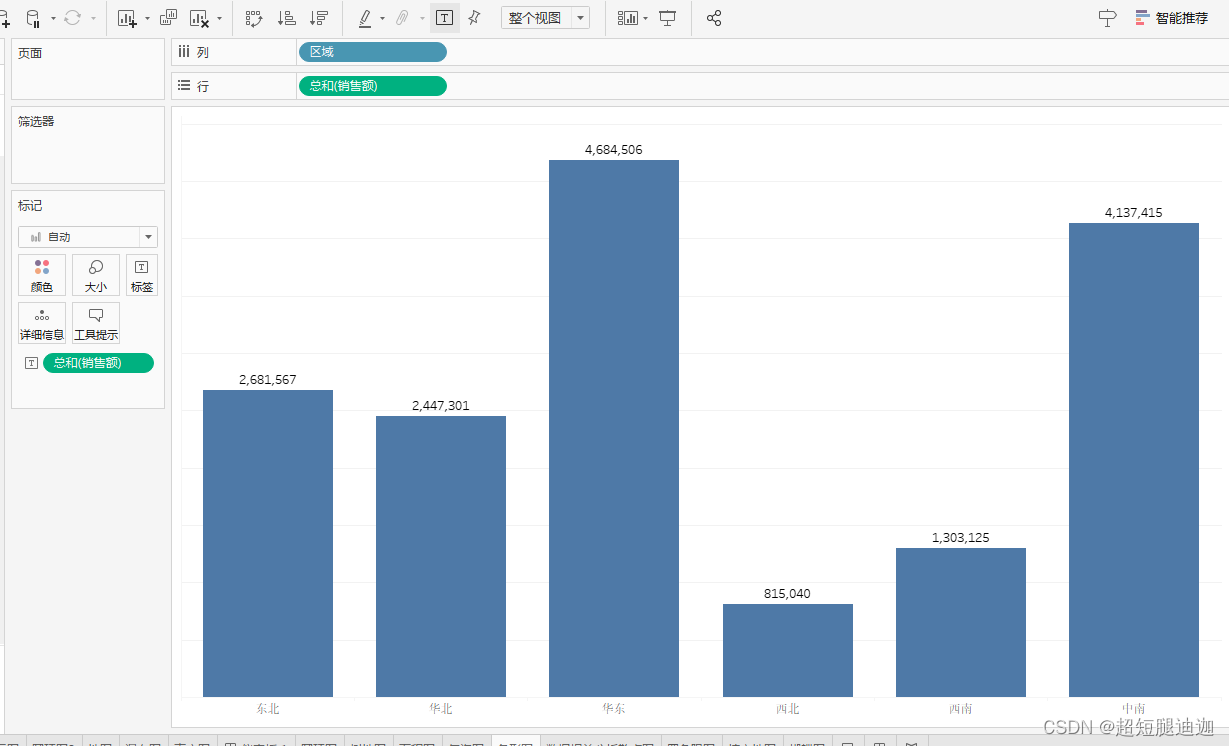
条形图
智能推荐水平条,再转置
词云图

拉好自己需要的数据 -> 点击智能推荐的树状图 ->将a改为文本
如需换色板 点击颜色 -> 编辑颜色
双轴图
智能推荐双组合图
或者使用双轴

气泡图
a改成圆
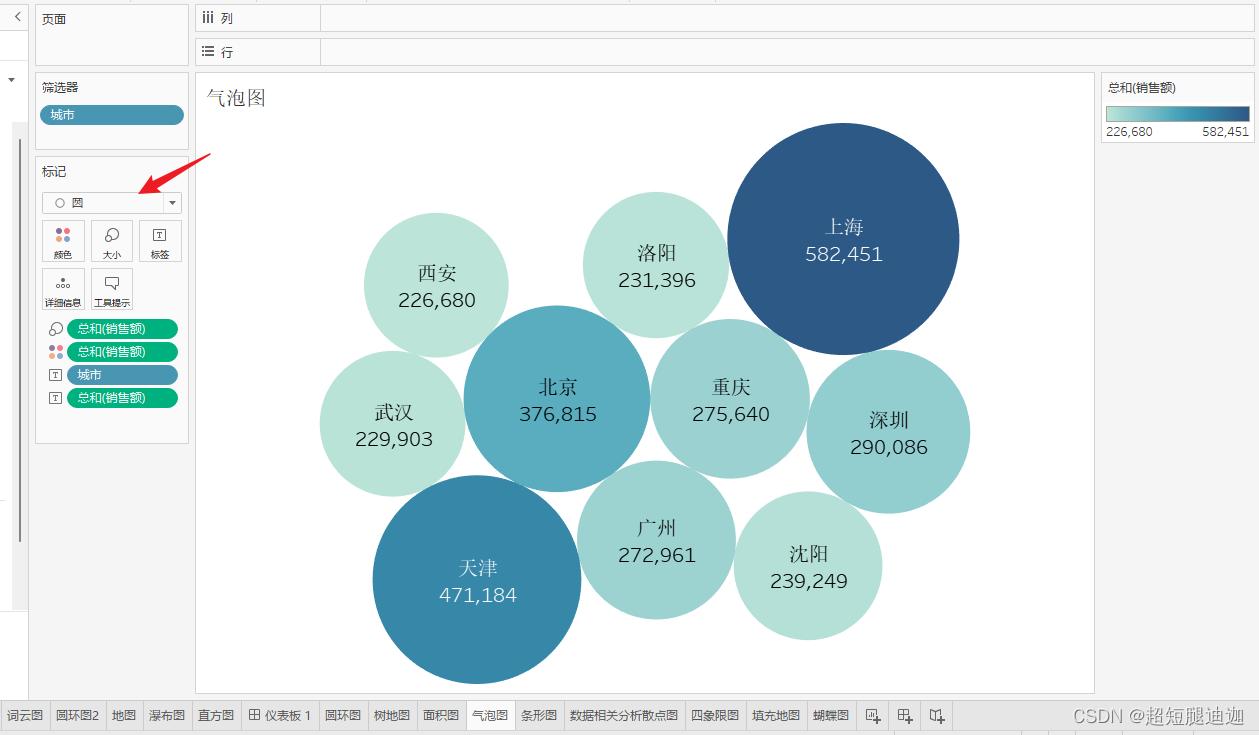
拉好数据之后智能推荐点击树状图
将a改为圆,调整大小
相关文章:

Tableau画图
目录 蝴蝶图 四象图 排序图 盒型图/散点图 圆环图 火柴图 直方图 瀑布图 地理图 面积图 树地图 面积图 条形图 词云图 双轴图 填充地图 tableau2023.2 须知 蝴蝶图 拉好数据之后 创建新字段正负销售额,并拖入第一个颜色标记卡 四象图 智能推荐 散…...
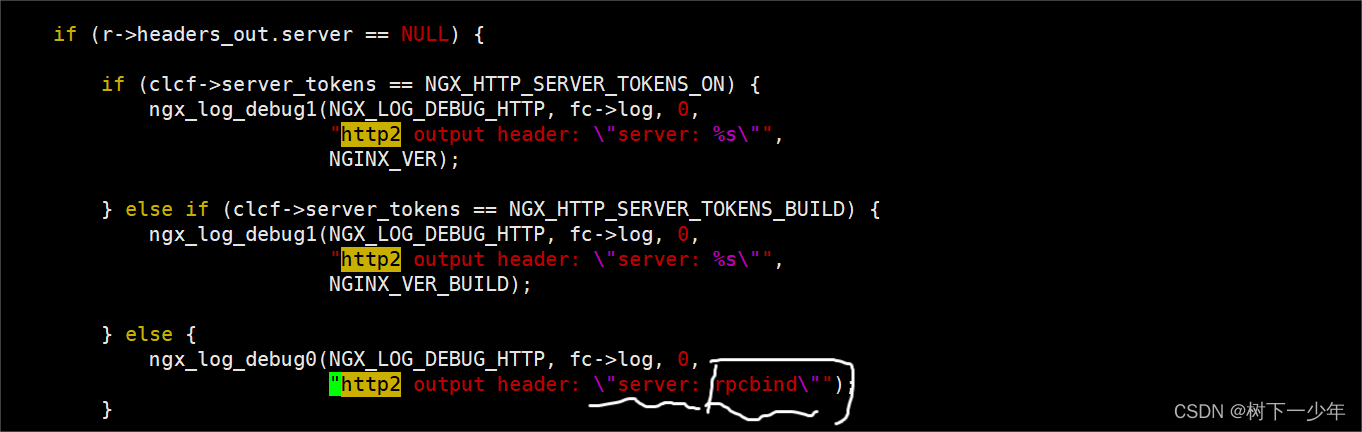
nginx上web服务的基本安全优化、服务性能优化、访问日志优化、目录资源优化和防盗链配置简介
一.基本安全优化 1.隐藏nginx软件版本信息 2.更改源码来隐藏软件名和版本 (1)修改第一个文件(核心头文件),在nginx安装目录下找到这个文件并修改 (2)第二个文件 (3)…...

himall3.0商城源码
目录 1 himall3.0商城源码 1.1 /// 获取待评价订单数量 1.2 /// 保存支付订单信息,生成支付订单 1.3 /// 取最近time分钟内的满足打印的订单数据 himall3.0商城源码 /// <summary>...

【LeetCode75】第二十九题 删除链表的中间节点
目录 题目: 示例; 分析: 代码: 题目: 示例; 分析: 给我们一个链表,让我们把链表中间的节点删了。 那么最直观最基础的办法是遍历两边链表,第一遍拿到链表长度,第二次把链表中间节点删了。 这个暴力做法我没事过…...

Floyd(多源汇最短路)
Floyd求最短路 给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,边权可能为负数。 再给定 k 个询问,每个询问包含两个整数 x 和 y,表示查询从点 x 到点 y 的最短距离,如果路径不存在,则输出 impo…...
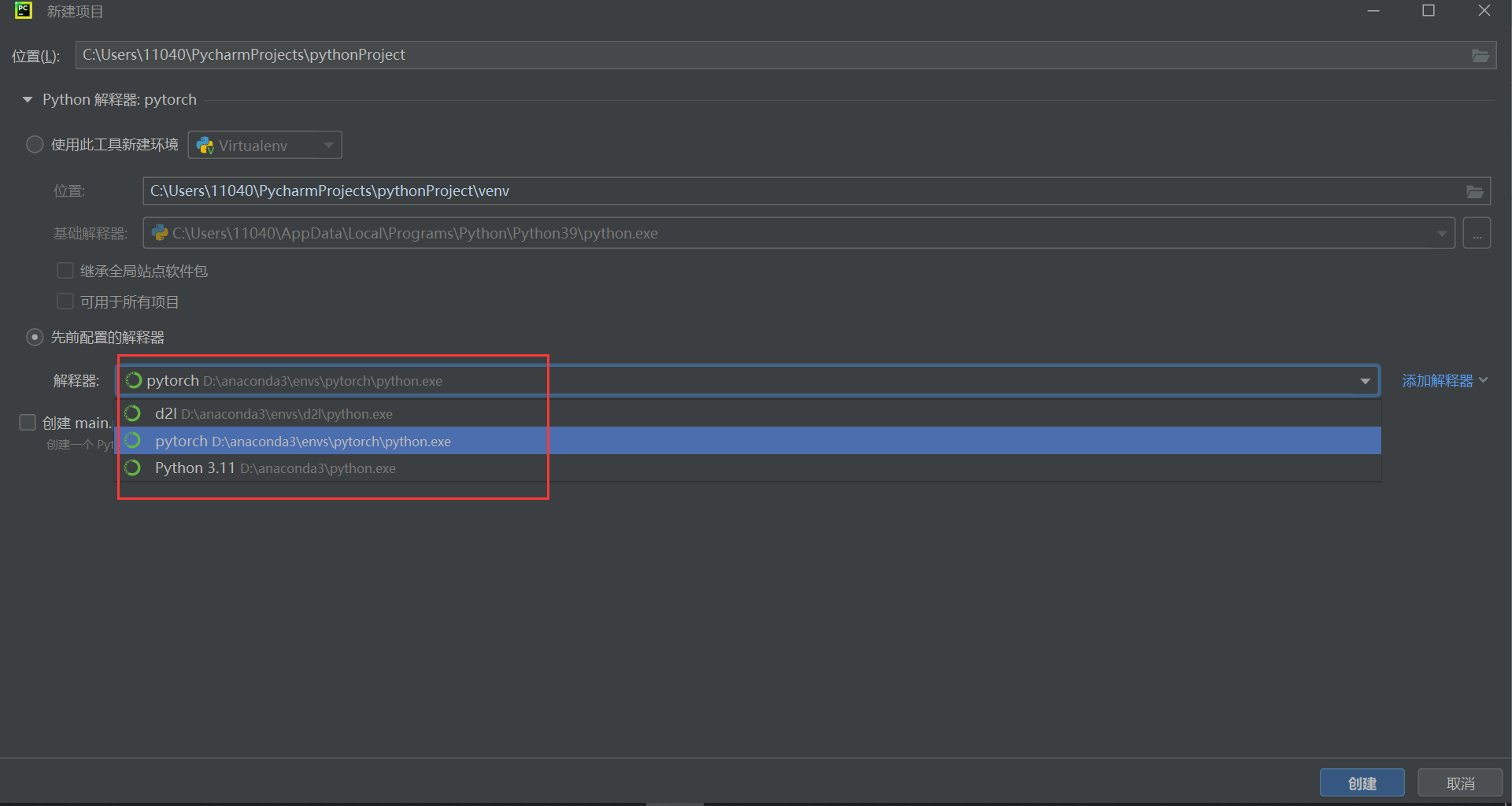
Pycharm找不到Conda可执行文件路径(Pycharm无法导入Anaconda已有环境)
在使用Pycharm时发现无法导入Anaconda创建好的环境,会出现找不到Conda可执行文件路径的问题。 解决 在输入框内输入D:\anaconda3\Scripts\conda.exe,点击加载环境。 注意前面目录是自己Anaconda的安装位置,之后就可以找到Anaconda的现有环…...

国产之光:讯飞星火最新大模型V2.0
大家好,我是herosunly。985院校硕士毕业,现担任算法研究员一职,热衷于机器学习算法研究与应用。曾获得阿里云天池比赛第一名,CCF比赛第二名,科大讯飞比赛第三名。拥有多项发明专利。对机器学习和深度学习拥有自己独到的…...
通讯录实现【C语言】
目录 前言 一、整体逻辑分析 二、实现步骤 1、创建菜单和多次操作问题 2、创建通讯录 3、初始化通讯录 4、添加联系人 5、显示联系人 6、删除指定联系人 7、查找指定联系人 8、修改联系人信息 9、排序联系人信息 三、全部源码 前言 我们上期已经详细的介绍了自定…...

pcl欧式聚类
欧式聚类实现方法大致是: 1、找到空间中某点 p 1 p_1 p1,用KD-Tree找到离他最近的n个点,判断这n个点到 p 1 p_1 p1的距离。将距离小于阈值r的点 p 2 、 p 3 、 p 4 p_2、p_3、p_4 p2、p3、p4…放在类Q里 2、在 Q ( p 1 ) Q(p_1…...
macOS Ventura 13.5.1(22G90)发布(附黑/白苹果系统镜像地址)
系统镜像下载:百度:黑果魏叔 系统介绍 黑果魏叔 8 月 18 日消息,苹果今日向 Mac 电脑用户推送了 macOS 13.5.1 更新(内部版本号:22G90),本次更新距离上次发布隔了 24 天。 本次更新重点修复了…...

分布式监控平台——Zabbix
市场上常用的监控软件: 传统运维:zabbix、 Nagios 一、zabbix概述 作为一个运维,需要会使用监控系统查看服务器状态以及网站流量指标,利用监控系统的数据去了解上线发布的结果,和网站的健康状态。 利用一个优秀的监…...
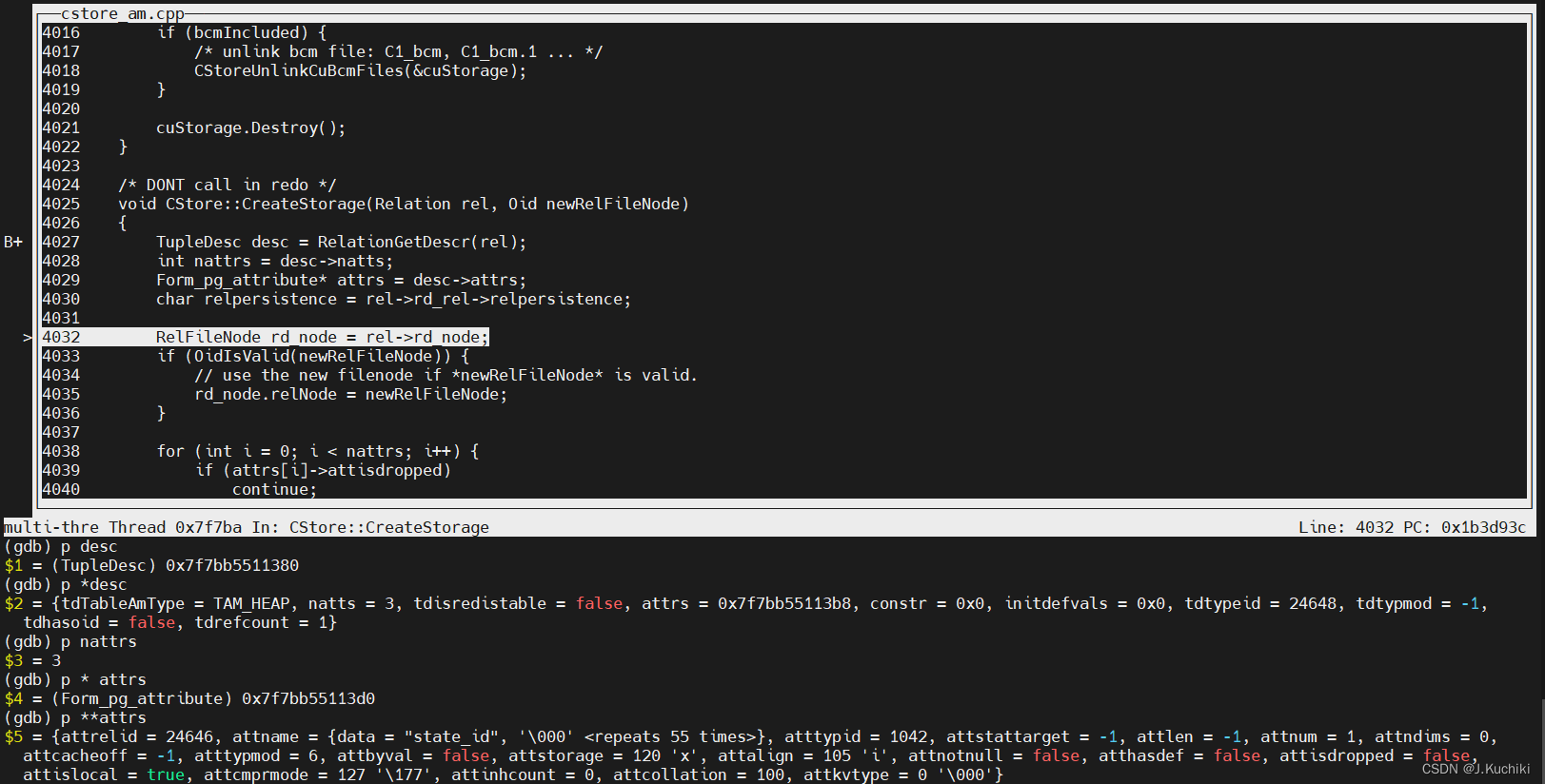
【OpenGauss源码学习 —— 列存储(创建表)】
列存储 什么是列存储?语法实现语法格式参数说明示例源码分析(创建表)语法层(Gram.y)子模块(utility.cpp) 总结 声明:本文的部分内容参考了他人的文章。在编写过程中,我们…...
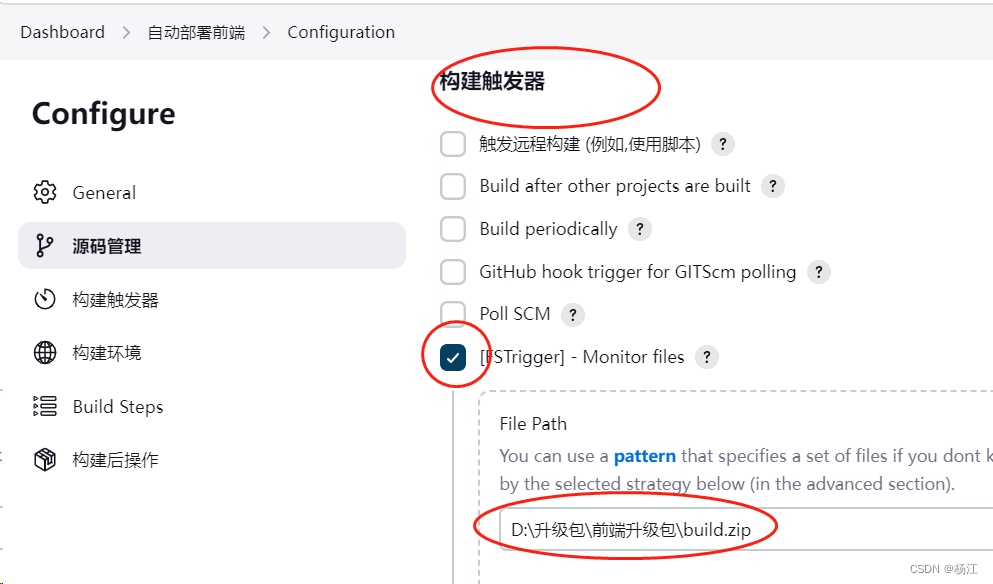
Jenkins 监控dist.zip文件内容发生变化 触发自动部署
为Jenkins添加plugin http://xx:xx/manage 创建一个任务 构建触发器 每3分钟扫描一次,发现指定文件build.zip文件的MD5发生变化后 触发任务...
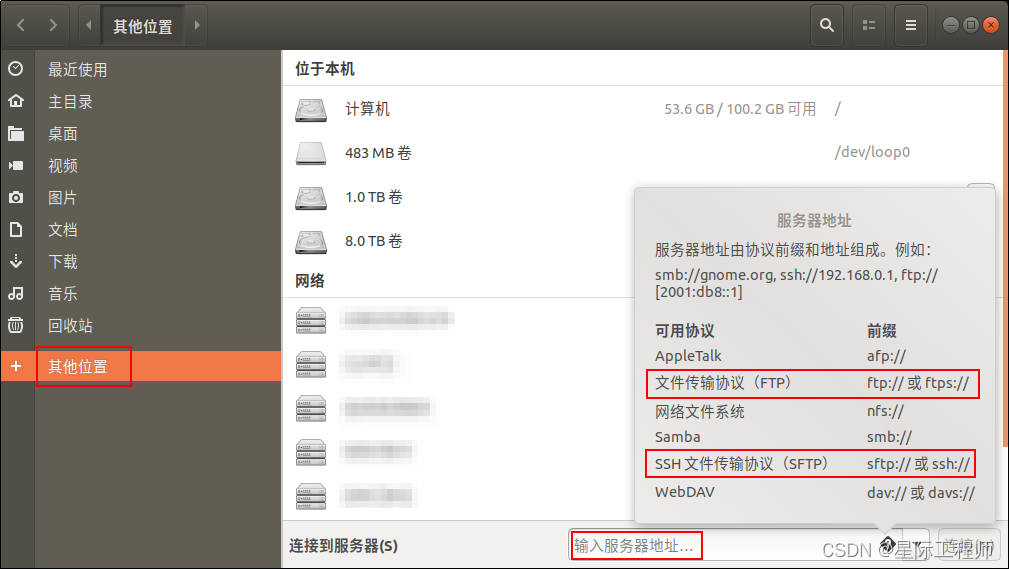
Linux系列讲解 —— FTP协议的应用
简单介绍一下FTP文件传输协议在linux系统中的应用。 目录 0. 基本概念1. FTP Server1.1 安装FTP Server1.2 FTP Server开启和关闭1.3 查看FTP Server是否开启1.4 FTP服务器配置 2. FTP Client2.1 lftp2.2 ftp2.3 sftp2.4 文件资源管理器集成的ftp和sftp 3. ftp常用命令 0. 基本…...

Rancher-RKE-install 部署k8s集群
一、为什么用Rancher-RKE-install 1.CNCF认证的k8s安装程序。 2.有中文文档。 二、安装步骤 1.下载Rancher-Rke的二进制包-下面是项目的地址 GitHub - rancher/rke: Rancher Kubernetes Engine (RKE), an extremely simple, lightning fast Kubernetes distrib…...

PHP8的正则表达式-PHP8知识详解
在网页程序的时候,经常会有查找符合某些复杂规则的字符串的需求。正则表达式就是描述这些规则的工具。 正则表达式是把文本或者字符串按照一定的规范或模型表示的方法,经常用于文本的匹配操作。 例如:我们在填写手机号码的时候,…...
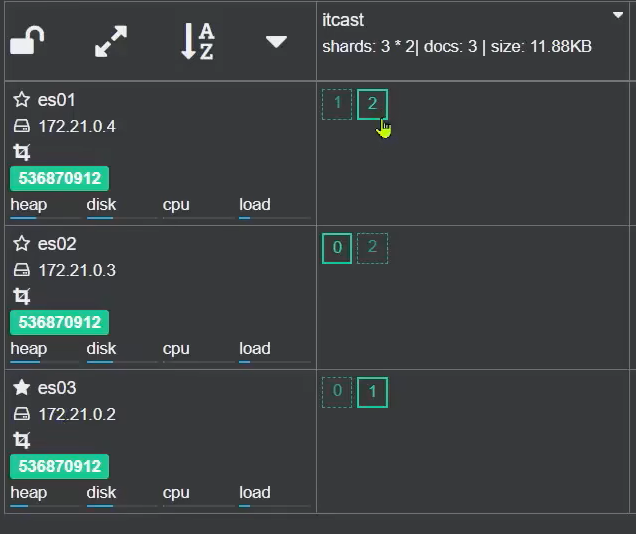
SpringCloud实用篇7——深入elasticsearch
目录 1 数据聚合1.1 聚合的种类1.2 DSL实现聚合1.2.1 Bucket聚合语法1.2.2 聚合结果排序1.2.3 限定聚合范围1.2.4 Metric聚合语法1.2.5.小结 1.3 RestAPI实现聚合1.3.1 API语法1.3.2 业务需求1.3.3 业务实现 2 自动补全2.1 拼音分词器2.2 自定义分词器2.3 自动补全查询2.4 实现…...

uni-app 经验分享,从入门到离职(二)—— tabBar 底部导航栏实战篇
文章目录 📋前言⏬关于专栏 🎯关于小程序 tabbar 的一些知识🎯创建一个基本的 tabBar📝最后 📋前言 这篇文章的内容主题是关于小程序的 tabBar 底部导航栏的入门使用和实战技巧。通过上一篇文章的基础,我们…...
:内存区域)
Java虚拟机(JVM):内存区域
一、内存区域介绍 Java虚拟机(JVM)内存可以分为以下几个区域: 程序计数器(Program Counter Register):用于记录当前线程执行的字节码指令的地址,属于线程私有的区域。在任意时刻,一…...
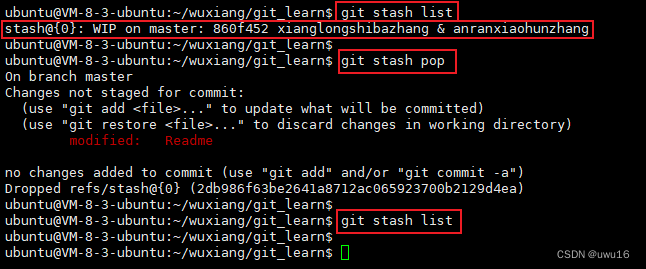
11 - git stash 开发中临时加塞了紧急任务怎么处理
查看所有文章链接:(更新中)GIT常用场景- 目录 文章目录 开发中临时加塞了紧急任务怎么处理 开发中临时加塞了紧急任务怎么处理 当你此时工作区已经修改了 Readme 文件,然后突然需要解决其他问题(紧急问题、新任务&…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

对象回调初步研究
_OBJECT_TYPE结构分析 在介绍什么是对象回调前,首先要熟悉下结构 以我们上篇线程回调介绍过的导出的PsProcessType 结构为例,用_OBJECT_TYPE这个结构来解析它,0x80处就是今天要介绍的回调链表,但是先不着急,先把目光…...

Qwen系列之Qwen3解读:最强开源模型的细节拆解
文章目录 1.1分钟快览2.模型架构2.1.Dense模型2.2.MoE模型 3.预训练阶段3.1.数据3.2.训练3.3.评估 4.后训练阶段S1: 长链思维冷启动S2: 推理强化学习S3: 思考模式融合S4: 通用强化学习 5.全家桶中的小模型训练评估评估数据集评估细节评估效果弱智评估和民间Arena 分析展望 如果…...

【字节拥抱开源】字节团队开源视频模型 ContentV: 有限算力下的视频生成模型高效训练
本项目提出了ContentV框架,通过三项关键创新高效加速基于DiT的视频生成模型训练: 极简架构设计,最大化复用预训练图像生成模型进行视频合成系统化的多阶段训练策略,利用流匹配技术提升效率经济高效的人类反馈强化学习框架&#x…...
