算法基础课——基础算法(模板整理)
快速排序
快速排序
#include <iostream>
#include <algorithm>
using namespace std;
int n;
int s[100000];
int main()
{cin>>n;for(int i=0;i<n;i++){cin>>s[i];}sort(s,s+n);for(int i=0;i<n;i++){cout<<s[i]<<" ";}cout<<endl;return 0;
}第K个数
#include <iostream>
#include <algorithm>
using namespace std;
int a[100005];
int main()
{int n,k;cin>>n>>k;for(int i=1;i<=n;i++){cin>>a[i];}nth_element(a+1,a+k,a+1+n);cout<<a[k]<<endl;return 0;
}归并排序
归并排序
#include <iostream>
using namespace std;
const int N = 100010;
int n;
int q[N],tmp[N];
void merge_sort(int q[],int l,int r)
{if(l>=r){return;}int mid=(l+r)>>1;merge_sort(q,l,mid);merge_sort(q,mid+1,r);int k=1,i=l,j=mid+1;while(i<=mid&&j<=r){if(q[i]<=q[j]){tmp[k++]=q[i++];}else{tmp[k++]=q[j++];}}while(i<=mid){tmp[k++]=q[i++];}while(j<=r){tmp[k++]=q[j++];}for(int i=l,j=1;i<=r;i++,j++){q[i]=tmp[j];}
}
int main()
{scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d",&q[i]);}merge_sort(q,1,n);for(int i=1;i<=n;i++){printf("%d ",q[i]);}return 0;
}逆序对的数量
#include <iostream>
using namespace std;
typedef long long ll;
const int N = 100010;
int n;
int q[N],tmp[N];
ll merge_sort(int l,int r)
{if(l>=r){return 0;}int mid = (l+r)>>1;ll res=merge_sort(l,mid)+merge_sort(mid+1,r);//归并的过程int k=1,i=l,j=mid+1;while(i<=mid&&j<=r){if(q[i]<=q[j]){tmp[k++]=q[i++];}else{tmp[k++]=q[j++];res+=(mid-i+1);}}//扫尾while(i<=mid){tmp[k++]=q[i++];}while(j<=r){tmp[k++]=q[j++];}//物归原主for(int i=l,j=1;i<=r;i++,j++){q[i]=tmp[j];}return res;
}
int main()
{cin>>n;for(int i=1;i<=n;i++){cin>>q[i];}cout<<merge_sort(1,n)<<endl;return 0;
}二分
数的范围
#include <iostream>
using namespace std;
const int N = 100010;
int q[N];
int main()
{int n,m;cin>>n>>m;for(int i=0;i<n;i++){cin>>q[i];}while(m--){int x;cin>>x;int l=0,r=n-1;while(l<r){int mid=l+r>>1;if(q[mid]>=x){r=mid;}else l=mid+1;}if(q[l]!=x){cout<<"-1 -1"<<endl;}else{cout<<l<<" ";l=0;r=n-1;while(l<r){int mid=l+r+1>>1;if(q[mid]<=x){l=mid;}else r=mid-1;}cout<<l<<endl;}}return 0;
}数的三次方根
#include <iostream>
using namespace std;
int main()
{double n;cin>>n;double l=-10000,r=10000;while(r-l>1e-8){double mid = (l+r)/2;if(mid*mid*mid>=n){r=mid;}else l=mid;}printf("%.6lf\n",l);return 0;
}高精度
高精度加法
Python一行就可以解决
print(int(input())+int(input()))#include <iostream>
#include <string>
#include <vector>
using namespace std;
vector<int> add(vector<int> &A,vector<int> &B)
{vector<int>C;int t=0;for(int i=0;i<A.size()||i<B.size();i++){if(i<A.size()){t+=A[i];}if(i<B.size()){t+=B[i];}C.push_back(t%10);t/=10;}if(t){C.push_back(t);}return C;
}
int main()
{string a,b;cin>>a>>b;vector<int>A,B;for(int i=a.size()-1;i>=0;i--){A.push_back(a[i]-'0');}for(int i=b.size()-1;i>=0;i--){B.push_back(b[i]-'0');}auto C = add(A,B);for(int i=C.size()-1;i>=0;i--){cout<<C[i];}return 0;
}高精度减法
#include <iostream>
#include <string>
#include <vector>
using namespace std;
//判断是否有A>=B
bool cmp(vector<int> &A,vector<int> &B)
{if(A.size()!=B.size()){return A.size()>B.size();}for(int i=A.size()-1;i>=0;i--){if(A[i]!=B[i]){return A[i]>B[i];}}return true;
}
//C=A-B
vector<int> sub(vector<int> &A,vector<int> &B)
{vector<int>C;int t=0;for(int i=0;i<A.size();i++){t=A[i]-t;if(i<B.size()){t-=B[i];}C.push_back((t+10)%10);if(t<0){t=1;}else t=0;}while(C.size()>1&&C.back()==0){C.pop_back();}return C;
}
int main()
{string a,b;cin>>a>>b;vector<int>A,B;for(int i=a.size()-1;i>=0;i--){A.push_back(a[i]-'0');}for(int i=b.size()-1;i>=0;i--){B.push_back(b[i]-'0');}if(cmp(A,B)){auto C = sub(A,B);for(int i=C.size()-1;i>=0;i--){cout<<C[i];}}else{auto C = sub(B,A);cout<<"-";for(int i=C.size()-1;i>=0;i--){cout<<C[i];}}return 0;
}高精度乘法
#include <iostream>
#include <vector>
using namespace std;
vector<int> mul(vector<int>& A, int b)
{vector<int>C;int t = 0;for (int i = 0; i < A.size() || t; i++){if (i < A.size()){t += A[i] * b;}C.push_back(t % 10);t /= 10;}while(C.size()>1&&C.back()==0){C.pop_back();}return C;
}
int main()
{string a;int b;cin >> a >> b;vector<int>A;for (int i = a.size() - 1; i >= 0; i--){A.push_back(a[i] - '0');}auto C = mul(A, b);for (int i = C.size() - 1; i >= 0; i--){cout << C[i];}return 0;
}高精度除法
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
vector<int> div(vector<int>& A, int b,int &r)
{vector<int>C;r=0;for (int i = A.size()-1; i >= 0; i--){r = r * 10 + A[i];C.push_back(r/b);r%=b;}reverse(C.begin(),C.end());while(C.size()>1&&C.back()==0){C.pop_back();}return C;
}
int main()
{string a;int b;cin >> a >> b;vector<int>A;for (int i = a.size() - 1; i >= 0; i--){A.push_back(a[i] - '0');}int r;auto C = div(A, b,r);for (int i = C.size() - 1; i >= 0; i--){cout << C[i];}cout<<endl<<r<<endl;return 0;
}前缀和与差分
前缀和
#include <iostream>
using namespace std;
const int N = 100005;
int a[N],s[N];
int main()
{int n,m;cin>>n>>m;for(int i=1;i<=n;i++){cin>>a[i];}for(int i=1;i<=n;i++){s[i]=s[i-1]+a[i];}while(m--){int l,r;cin>>l>>r;cout<<s[r]-s[l-1]<<endl;}return 0;
}子矩阵的和
#include <iostream>
using namespace std;
const int N = 1010;
int a[N][N], s[N][N];
int main()
{int n, m, q;cin >> n >> m >> q;for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++){scanf("%d", &a[i][j]);s[i][j] = s[i][j - 1] + s[i - 1][j] - s[i - 1][j - 1] + a[i][j]; // 求前缀和}while (q--) {int x1,y1,x2,y2;scanf("%d%d%d%d", &x1, &y1, &x2, &y2);// 算子矩阵的和printf("%d\n", s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1]); }return 0;
}差分
#include <iostream>
using namespace std;
const int N = 100010;
int n,m;
int a[N],b[N];
void insert(int l,int r,int c)
{b[l]+=c;b[r+1]-=c;
}
int main()
{cin>>n>>m;for(int i=1;i<=n;i++){cin>>a[i];}for(int i=1;i<=n;i++){insert(i,i,a[i]);}while(m--){int l,r,c;cin>>l>>r>>c;insert(l,r,c);}for(int i=1;i<=n;i++){b[i]+=b[i-1];}for(int i=1;i<=n;i++){cout<<b[i]<<" ";}return 0;
}差分矩阵
#include <iostream>
using namespace std;
const int N = 1010;
int n,m,q;
int a[N][N],b[N][N];
void insert(int x1,int y1,int x2,int y2,int c)
{b[x1][y1]+=c;b[x2+1][y1]-=c;b[x1][y2+1]-=c;b[x2+1][y2+1]+=c;
}
int main()
{cin>>n>>m>>q;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>a[i][j];}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){insert(i,j,i,j,a[i][j]);}}while(q--){int x1,y1,x2,y2,c;cin>>x1>>y1>>x2>>y2>>c;insert(x1,y1,x2,y2,c);}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1];}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cout<<b[i][j]<<" ";}cout<<endl;}return 0;
}双指针算法
最长连续不重复子序列
#include <iostream>
using namespace std;
const int N = 100010;
int n;
int a[N],s[N];
int main()
{cin>>n;for(int i=1;i<=n;i++){cin>>a[i];}int res=0;for(int i=1,j=1;i<=n;i++){s[a[i]]++;while(s[a[i]]>1){s[a[j]]--;j++;}res=max(res,i-j+1);}cout<<res<<endl;return 0;
}数组元素的目标和
#include <iostream>
using namespace std;
const int N = 100005;
int n,m,x;
int a[N],b[N];
int main()
{cin>>n>>m>>x;for(int i=1;i<=n;i++){cin>>a[i];}for(int i=1;i<=m;i++){cin>>b[i];}for(int i=1,j=m;i<=n;i++){while(j>=1&&a[i]+b[j]>x) j--;if(a[i]+b[j]==x){cout<<i-1<<" "<<j-1<<endl;break;}}return 0;
}判断子序列
#include <iostream>
using namespace std;
const int N = 100005;
int n,m;
int a[N],b[N];
int main()
{cin>>n>>m;for(int i=0;i<n;i++){cin>>a[i];}for(int i=0;i<m;i++){cin>>b[i];}int i=0,j=0;while(i<n&&j<m){if(a[i]==b[j])i++;j++;}if(i==n){cout<<"Yes"<<endl;}else{cout<<"No"<<endl;}return 0;
}位运算
二进制中1的个数
#include <iostream>
using namespace std;
int lowbit(int x)
{return x & -x;
}
int main()
{int n;cin>>n;while(n--){int x;cin>>x;int res=0;while(x){x-=lowbit(x);res++;}cout<<res<<" ";}return 0;
}离散化
区间和
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 300010; //n次插入和m次查询相关数据量的上界
int n, m;
int a[N];//存储坐标插入的值
int s[N];//存储数组a的前缀和
vector<int> alls; //存储(所有与插入和查询有关的)坐标
vector<pair<int, int>> add, query; //存储插入和询问操作的数据int find(int x)
{ //返回的是输入的坐标的离散化下标int l = 0, r = alls.size() - 1;while (l < r) {int mid = l + r >> 1;if (alls[mid] >= x) r = mid;else l = mid + 1;}return r + 1;
}int main()
{scanf("%d%d", &n, &m);for (int i = 1; i <= n; i++) {int x, c;scanf("%d%d", &x, &c);add.push_back({x, c});alls.push_back(x);}for (int i = 1; i <= m; i++) {int l , r;scanf("%d%d", &l, &r);query.push_back({l, r});alls.push_back(l);alls.push_back(r);}//排序,去重sort(alls.begin(), alls.end());alls.erase(unique(alls.begin(), alls.end()), alls.end());//执行前n次插入操作for (auto item : add) {int x = find(item.first);a[x] += item.second;}//前缀和for (int i = 1; i <= alls.size(); i++) s[i] = s[i-1] + a[i];//处理后m次询问操作for (auto item : query) {int l = find(item.first);int r = find(item.second);printf("%d\n", s[r] - s[l-1]);}return 0;
}区间和并
区间和并
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
typedef pair<int,int>pii;
const int N = 100010;
int n;
vector<pii>segs;
void merge(vector<pii>&segs)
{vector<pii>res;sort(segs.begin(),segs.end());int st=-2e9,ed=-2e9;for(auto seg:segs){if(ed<seg.first){if(ed!=-2e9) res.push_back({st,ed});st=seg.first;ed=seg.second;}else ed=max(ed,seg.second);}if(st!=2e9) res.push_back({st,ed});cout<<res.size()<<endl;
}
int main()
{cin>>n;for(int i=0;i<n;i++){int l,r;cin>>l>>r;segs.push_back({l,r});}merge(segs);return 0;
}相关文章:
)
算法基础课——基础算法(模板整理)
快速排序 快速排序 #include <iostream> #include <algorithm> using namespace std; int n; int s[100000]; int main() {cin>>n;for(int i0;i<n;i){cin>>s[i];}sort(s,sn);for(int i0;i<n;i){cout<<s[i]<<" ";}cout<…...
如何解决使用npm出现Cannot find module ‘XXX\node_modules\npm\bin\npm-cli.js’错误
遇到问题:用npm下载组件时出现Cannot find module ‘D:software\node_modules\npm\bin\npm-cli.js’ 问题,导致下载组件不能完成。 解决方法:下载缺少的npm文件即可解决放到指定node_modules目录下即可解决。 分析问题࿱…...
【华为认证数通高级证书实验-分享篇2】
实验拓扑 注:代码块为各交换机路由器中的配置命令 配置拓扑文件 实验要求 实现全网通 实验配置 SW3 [SW3]v b 10 20 [SW3]int e0/0/1 [SW3-Ethernet0/0/1]po link-t a [SW3-Ethernet0/0/1]po de v 10 [SW3-Ethernet0/0/1]int e0/0/2 [SW3-Ethernet0/0/2]po li…...

ui设计需要学编程吗难不难学习 优漫动游
ui设计需要学编程吗难不难学习,对于基础小白来说学习编程确实有一定难度,所以很想知道零基础学习ui设计需要学编程吗,需不需要写代码呢,这些问题小编来简单的分析分析解决零基础小白的一些困惑,希望对你有帮助。 ui…...

什么是线程优先级?Java中的线程优先级是如何定义和使用的?
线程优先级是指在多线程环境中,通过给线程分配不同的优先级来决定线程获取CPU时间片的顺序。优先级较高的线程会更有可能被调度执行,而优先级较低的线程可能会获得较少的CPU时间。 在Java中,线程优先级是通过整数表示的,范围从1到…...

无涯教程-TensorFlow - XOR实现
在本章中,无涯教程将学习使用TensorFlow的XOR实现,在TensorFlow中开始XOR实施之前,看一下XOR表值。这将帮助了解加密和解密过程。 A B A XOR B 0 0 0 0 1 1 1 0 1 1 1 0 XOR密码加密方法基本上用于加密,即通过生成与适当密钥匹配…...

计算机组成与设计 Patterson Hennessy 笔记(二)MIPS 指令集
计算机的语言:汇编指令集 也就是指令集。本书主要介绍 MIPS 指令集。 汇编指令 算数运算: add a,b,c # abc sub a,b,c # ab-cMIPS 汇编的注释是 # 号。 由于MIPS中寄存器大小32位,是基本访问单位,因此也被称为一个字 word。M…...
)
【设计模式】模板方法模式(Template Method Pattern)
23种设计模式之模板方法模式(Template Method Pattern) 基本概念 模板方法模式是一种行为型设计模式,它定义了一个算法骨架,将某些算法步骤的实现延迟到子类中。 这样可以使得算法的框架不被修改,但是具体的实现可以…...

【潮州饶平】联想 IBM x3850 x6 io主板故障 服务器维修
哈喽 最近比较忙也好久没有更新服务器维修案例了,这次分享一例潮州市饶平县某企业工厂一台IBM System x3850 x6服务器亮黄灯告警且无法正常开机的服务器故障问题。潮州饶平ibm服务器维修IO主板故障问题 故障如下图所示: 故障服务器型号:IBM 或…...
【AIGC】 国内版聊天GPT
国内版聊天GPT 引言一、国内平台二、简单体验2.1 提问2.2 角色扮演2.3 总结画图 引言 ChatGPT是OpenAI发开的聊天程序,功能强大,可快速获取信息,节省用户时间和精力,提供个性化的服务。目前国产ChatGPT,比如文心一言&a…...

如何在Vue中进行单元测试?什么是Vue的模块化开发?
1、如何在Vue中进行单元测试? 在Vue中进行单元测试可以提高代码的可维护性和可读性,同时也能够帮助开发者更快地找到代码中的问题和潜在的错误。下面是一些在Vue中进行单元测试的步骤: 安装单元测试工具 首先需要安装一个单元测试工具&…...

Matlab编程示例3:Matlab求二次积分的编程示例
1.在MATLAB中,可以使用符号计算工具箱(Symbolic Math Toolbox)中的int函数来求解二次积分。 2.下面是一个简单的MATLAB程序示例,演示二次函数f (x,y) x^2 y^2,在x∈[0 1]和y∈[0 1]的积分区间上,计算积分结果: syms…...
【Linux】线程同步和死锁
目录 死锁 什么是死锁 构成死锁的四个必要条件 如何避免死锁 线程同步 同步的引入 同步的方式 条件变量 条件变量的使用 整体代码 死锁 什么是死锁 死锁是指在一组进程中的各个进程均占有不会释放的资源,但因互相申请被其他进程所占用不会释放 的资源而处…...
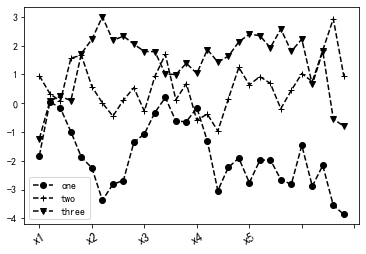
Matplotlib数据可视化(二)
目录 1.rc参数设置 1.1 lines.linestype取值 1.2 lines.marker参数的取值 1.3 绘图中文预设 1.4 示例 1.4.1 示例1 1.4.2 示例2 1.rc参数设置 利用matplotlib绘图时为了让绘制出的图形更加好看,需要对参数进行设置rc参数设置。可以通过以下代码查看matplotli…...

图像去雨-雨线清除-图像处理-(计算机作业附代码)
背景 多年来,图像去雨已经被广泛研究,使用传统方法和基于学习的方法。然而,传统方法如高斯混合模型和字典学习方法耗时,并且无法很好地处理受到严重雨滴影响的图像块。 算法 通过考虑雨滴条状特性和角度分布,这个问…...
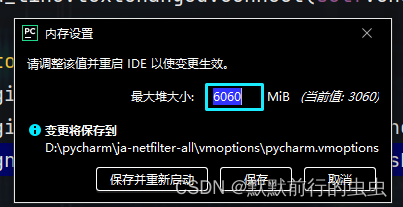
pycharm调整最大堆发挥最大
python程序运行时,怎么提高效率,设置pycharm最大堆过程如下; 一、进入设置pycharm最大堆; 二、进入设置pycharm最大堆; 如果8g设置为6g左右,占75%左右最佳...

uni-app 经验分享,从入门到离职(二)—— tabBar 底部导航栏实战基础篇
文章目录 📋前言⏬关于专栏 🎯关于小程序 tabbar 的一些知识🎯创建一个基本的 tabBar📝最后 📋前言 这篇文章的内容主题是关于小程序的 tabBar 底部导航栏的入门使用和实战技巧。通过上一篇文章的基础,我们…...
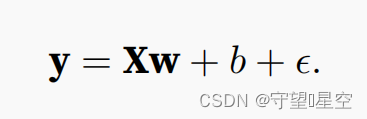
【李沐】3.2线性回归从0开始实现
%matplotlib inline import random import torch from d2l import torch as d2l1、生成数据集: 看最后的效果,用正态分布弄了一些噪音 上面这个具体实现可以看书,又想了想还是上代码把: 按照上面生成噪声,其中最后那…...
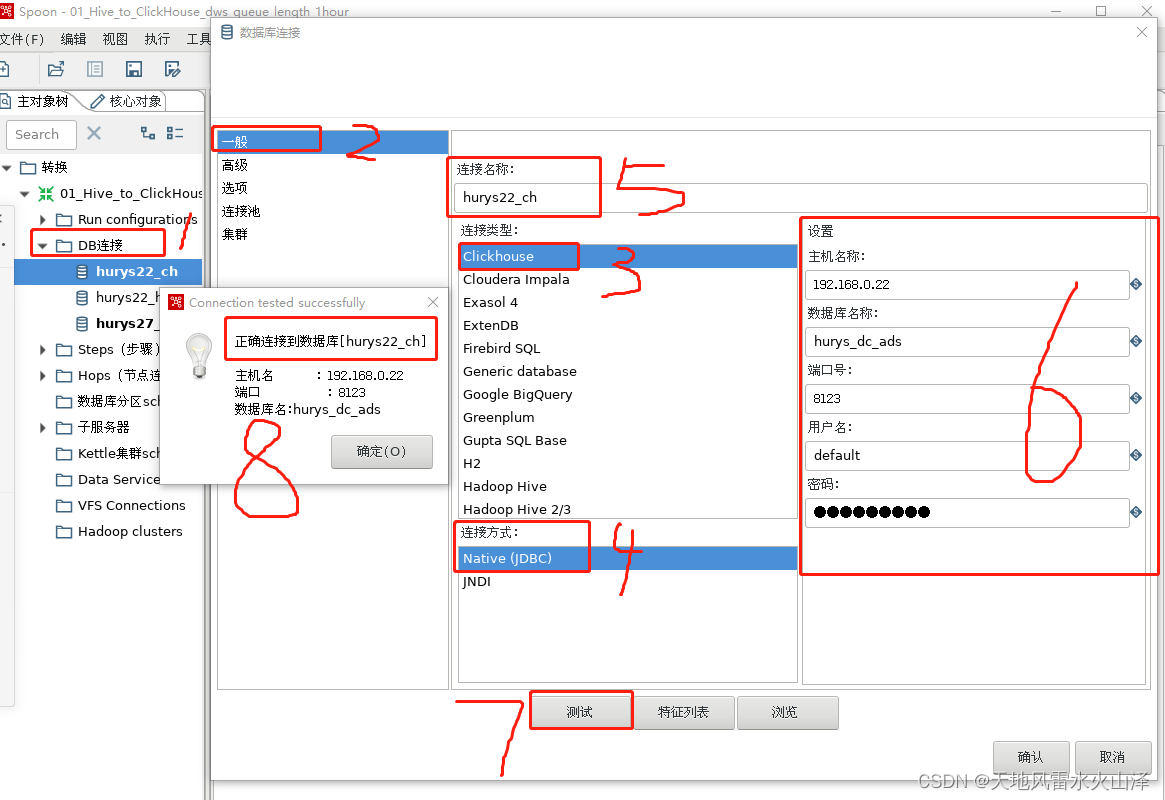
一百五十六、Kettle——Linux上安装的Kettle9.3连接ClickHouse数据库(亲测,附流程截图)
一、目标 kettle9.3在Linux上安装好后,需要与ClickHouse数据库建立连接 二、前提准备 (一)在Linux已经安装好kettle并可以启动kettle (二)已知kettle和ClickHouse版本 1、kettle版本是9.3 2、ClickHouse版本是21…...
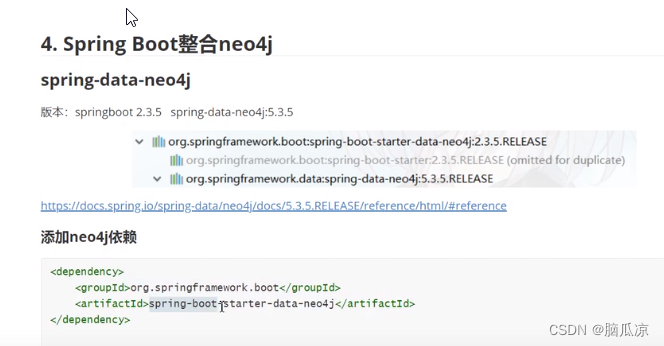
图数据库_Neo4j和SpringBoot整合使用_创建节点_删除节点_创建关系_使用CQL操作图谱---Neo4j图数据库工作笔记0009
首先需要引入依赖 springboot提供了一个spring data neo4j来操作 neo4j 可以看到它的架构 这个是下载下来的jar包来看看 有很多cypher对吧 可以看到就是通过封装的驱动来操作graph database 然后开始弄一下 首先添加依赖...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...
