Android 13.0 强制app横屏显示
1.概述
在13.0产品定制化开发中,对于处理屏幕旋转方向,首先有kernel底层处理,从底层驱动gsensor 中获取数据,从而判断屏幕方向的,然后事件上报后 最后由WMS就是WindowManagerService 来处理旋转的相关事件
2.强制app横屏显示的核心类
/framework/base/services/java/com/android/server/wm/DisplayRotation.java3.强制app横屏显示核心功能分析和处理
在系统中wms主要是处理屏幕相关的核心类,WMS中在处理屏幕自动旋转,主要是调用
DisplayRotation的freezeRotation方法锁定用户指定的屏幕方向,调用thawRotation方法,解锁用户固定屏幕,
恢复屏幕自动旋转。最后调用updateRotationUnchecked,发送新的Configuration变化,
以及如果布局发生变化,也会重新计算布局。
关于处理屏幕方法的api在13.0的系统中也是DisplayRotation.java 里负责处理的,
具体需要看源码然后分析具体的旋转功能
路径为:/framework/base/services/java/com/android/server/wm/DisplayRotation.java
int rotationForOrientation(int orientation, int lastRotation) {
if (DEBUG_ORIENTATION) {
Slog.v(TAG, "rotationForOrientation(orient="
+ orientation + ", last="相关文章:

Android 13.0 强制app横屏显示
1.概述 在13.0产品定制化开发中,对于处理屏幕旋转方向,首先有kernel底层处理,从底层驱动gsensor 中获取数据,从而判断屏幕方向的,然后事件上报后 最后由WMS就是WindowManagerService 来处理旋转的相关事件 2.强制app横屏显示的核心类 /framework/base/services/java/com…...

平方数之和(力扣)双指针 JAVA
给定一个非负整数 c ,你要判断是否存在两个整数 a 和 b,使得 a^2 b^2 c 。 示例 1: 输入:c 5 输出:true 解释:1 * 1 2 * 2 5 示例 2: 输入:c 3 输出&am…...

深入浅出Pytorch函数——torch.nn.init.sparse_
分类目录:《深入浅出Pytorch函数》总目录 相关文章: 深入浅出Pytorch函数——torch.nn.init.calculate_gain 深入浅出Pytorch函数——torch.nn.init.uniform_ 深入浅出Pytorch函数——torch.nn.init.normal_ 深入浅出Pytorch函数——torch.nn.init.c…...

OpenCV实现BGR2BayerGB/BG格式的转换
1、说明 OpenCV没有提供从BGR生成Bayer格式的接口,需要自己写 OpenCV定义为4种格式,分别为: BGGR排列 -> RG格式 RGGB排列 -> BG格式 GRBG排列 -> GB格式 GBRG排列 -> GR格式 2、转换 void CUtils::BGR2BayerGB(const cv::Mat &matSrc, cv::Mat &matDst)…...

Gateway网关路由以及predicates用法(项目中使用场景)
1.Gatewaynacos整合微服务 服务注册在nacos上,通过Gateway路由网关配置统一路由访问 这里主要通过yml方式说明: route: config: #type:database nacos yml data-type: yml group: DEFAULT_GROUP data-id: jeecg-gateway-router 配置路由:…...

深入浅出Pytorch函数——torch.nn.init.constant_
分类目录:《深入浅出Pytorch函数》总目录 相关文章: 深入浅出Pytorch函数——torch.nn.init.calculate_gain 深入浅出Pytorch函数——torch.nn.init.uniform_ 深入浅出Pytorch函数——torch.nn.init.normal_ 深入浅出Pytorch函数——torch.nn.init.c…...
)
centos mysql8解决Access denied for user ‘root‘@‘localhost‘ (using password: YES)
环境 系统:CentOS Stream release 9 mysql版本:mysql Ver 8.0.34 for Linux on x86_64 问题 mysql登录提示 Access denied for user rootlocalhost (using password: YES)解决方法 编辑 /etc/my.cnf ,在[mysqld] 部分最后添加一行 skip-…...

Docker实战:Docker常用命令
一、镜像相关 1.1、查看镜像 docker images1.2、拉取镜像 docker pull nginx1.3、保存镜像 docker save -o nginx.tar nginx:latest1.4、移除镜像 docker rmi -f nginx:latest1.5、导入镜像 docker load -i nginx.tar二、容器相关 2.1、启动容器 docker run --name red…...
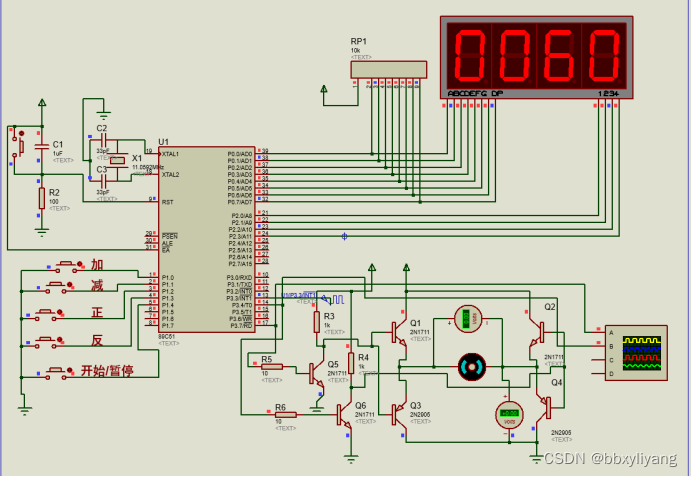
基于51单片机直流电机转速数码管显示控制系统
一、系统方案 本文主要研究了利用MCS-51系列单片机控制PWM信号从而实现对直流电机转速进行控制的方法。本文中采用了三极管组成了PWM信号的驱动系统,并且对PWM信号的原理、产生方法以及如何通过软件编程对PWM信号占空比进行调节,从而控制其输入信号波形等…...
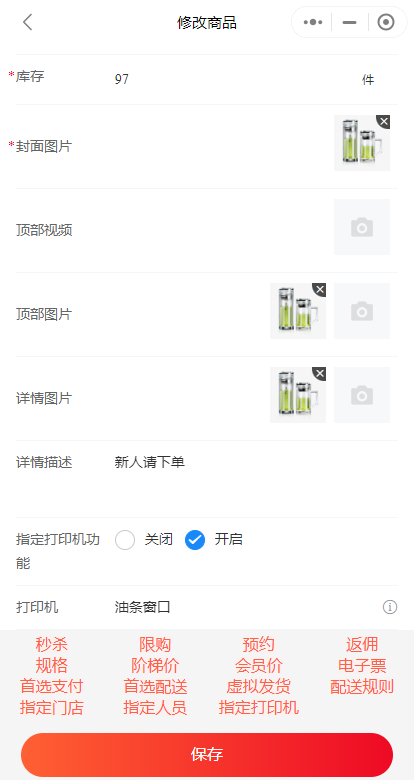
小程序商品如何指定打印机
有些商家,可能有多个仓库。不同的仓库,存放不同的商品。当客户下单时,小程序如何自动按照仓库拆分订单,如何让打印机自动打印对应仓库的订单呢?下面就来介绍一下吧。 1. 设置订单分发模式。进入管理员后台,…...

LLaMA-7B微调记录
Alpaca(https://github.com/tatsu-lab/stanford_alpaca)在70亿参数的LLaMA-7B上进行微调,通过52k指令数据(https://github.com/tatsu-lab/stanford_alpaca/blob/main/alpaca_data.json),在8个80GB A100上训…...
)
域名子目录发布问题(nginx、vue-element-admin、uni-app)
域名子目录发布问题(nginx、vue-element-admin、uni-app) 说明Vue-Element-Admin 代码打包nginx配置:uni-app打包 说明 使用一个域名下子目录进行打包: 比如: http://www.xxx.com/merchant 商户端代码 http://www.xx…...
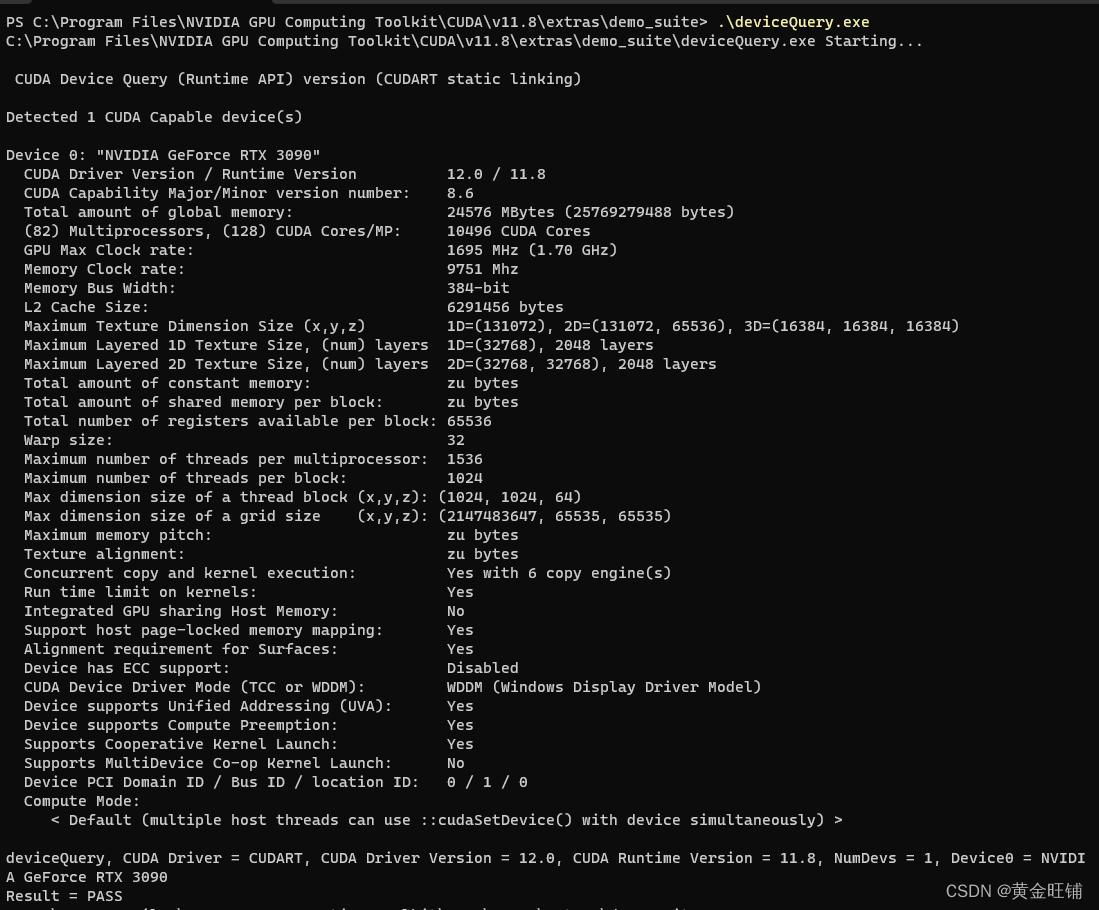
【环境配置】Windows 10 安装 PyTorch 开发环境,以及验证 YOLOv8
Windows 10 安装 PyTorch 开发环境,以及验证 YOLOv8 最近搞了一台Windows机器,准备在上面安装深度学习的开发环境,并搭建部署YOLOv8做训练和测试使用; 环境: OS: Windows 10 显卡: RTX 3090 安…...
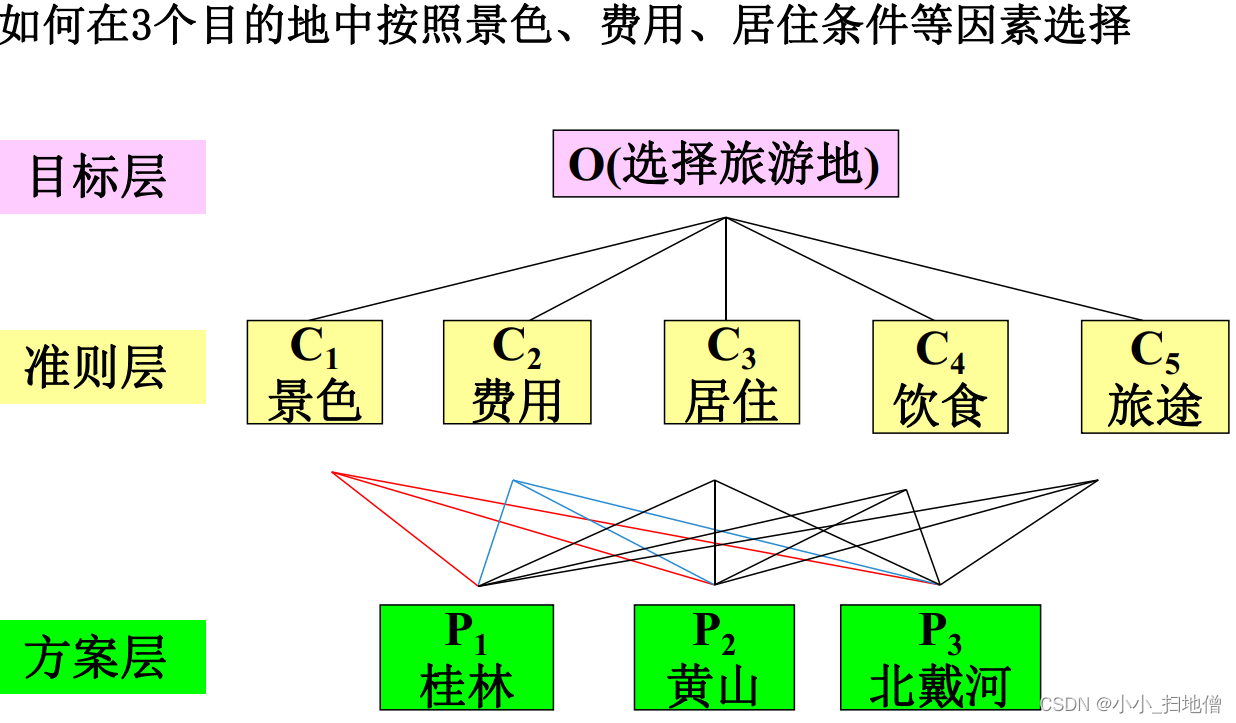
数学建模之“层次分析法”原理和代码详解
一、层次分析法简介 层次分析法(Analytic Hierarchy Process,AHP)是一种用于多准则决策分析和评估问题的定量方法,常用于数学建模中。它是由数学家托马斯赛蒂(Thomas Saaty)开发的。 层次分析法将复杂的决…...

使用IText导出复杂pdf
1、问题描述 需要将发票导出成pdf,要求每页都必须包含发票信息和表头行。 2、解决方法 使用IText工具实现PDF导出 IText8文档:Examples (itextpdf.com) 3、我的代码 引入Itext依赖,我这里用的是8.0.1版本 <dependency><groupId>…...
多线程并发服务器(TCP)
服务器 客户端 结果...
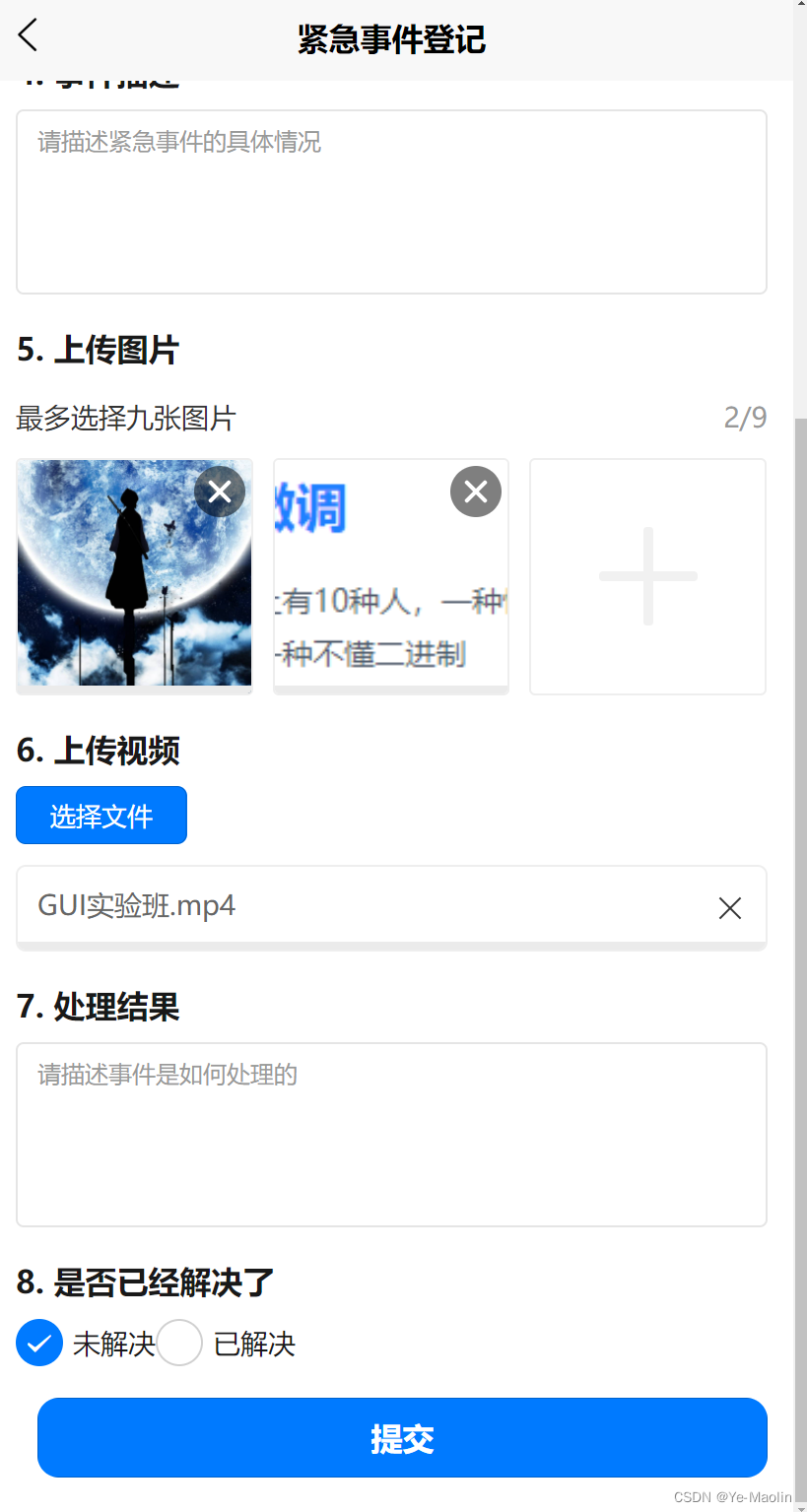
uni-app的Vue.js实现微信小程序的紧急事件登记页面功能
主要功能实现 完成发生时间选择功能,用户可以通过日期选择器选择事件发生的时间。实现事件类型选择功能,用户可以通过下拉选择框选择事件的类型。添加子养殖场编号输入框,用户可以输入与事件相关的子养殖场编号。完成事件描述输入功能&#…...

面试题 17.16.按摩师
题目来源: leetcode题目,网址:面试题 17.16. 按摩师 - 力扣(LeetCode) 解题思路: 动态规划,对于第 i 个预约,若接下,其最大值为不接上一个时的最大值与当前值之和&a…...
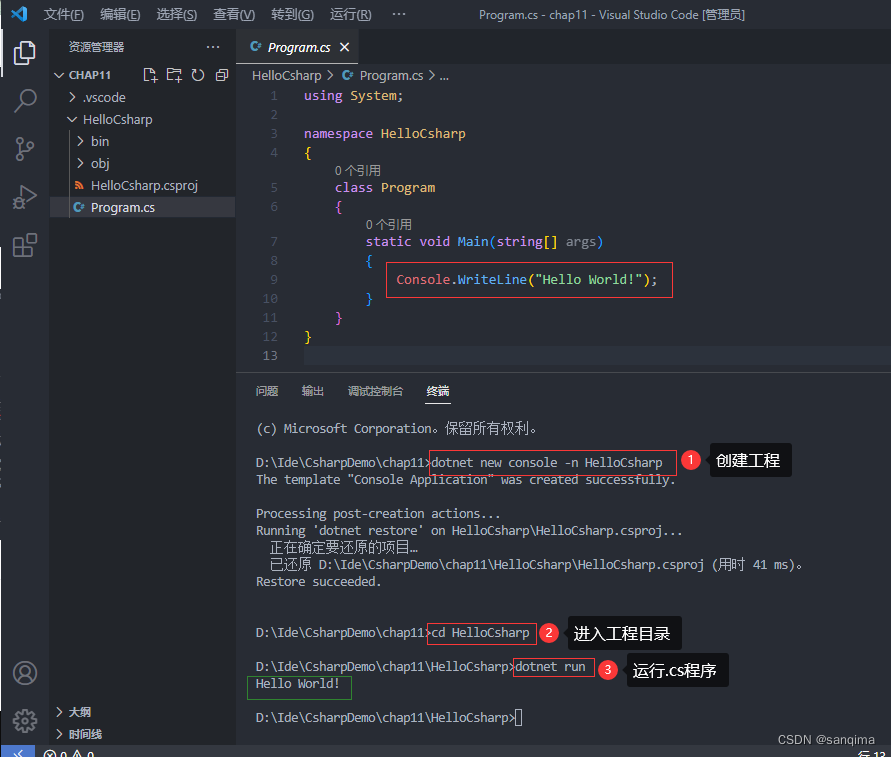
vscode里配置C#环境并运行.cs文件
vscode是一款跨平台、轻量级、开源的IDE, 支持C、C、Java、C#、R、Python、Go、Nodejs等多种语言的开发和调试。下面介绍在vscode里配置C#环境。这里以配置.Net SDK v5.0,语言版本为C#9.0,对应的开发平台为VS2019,作为案例说明。 1、下载vsc…...
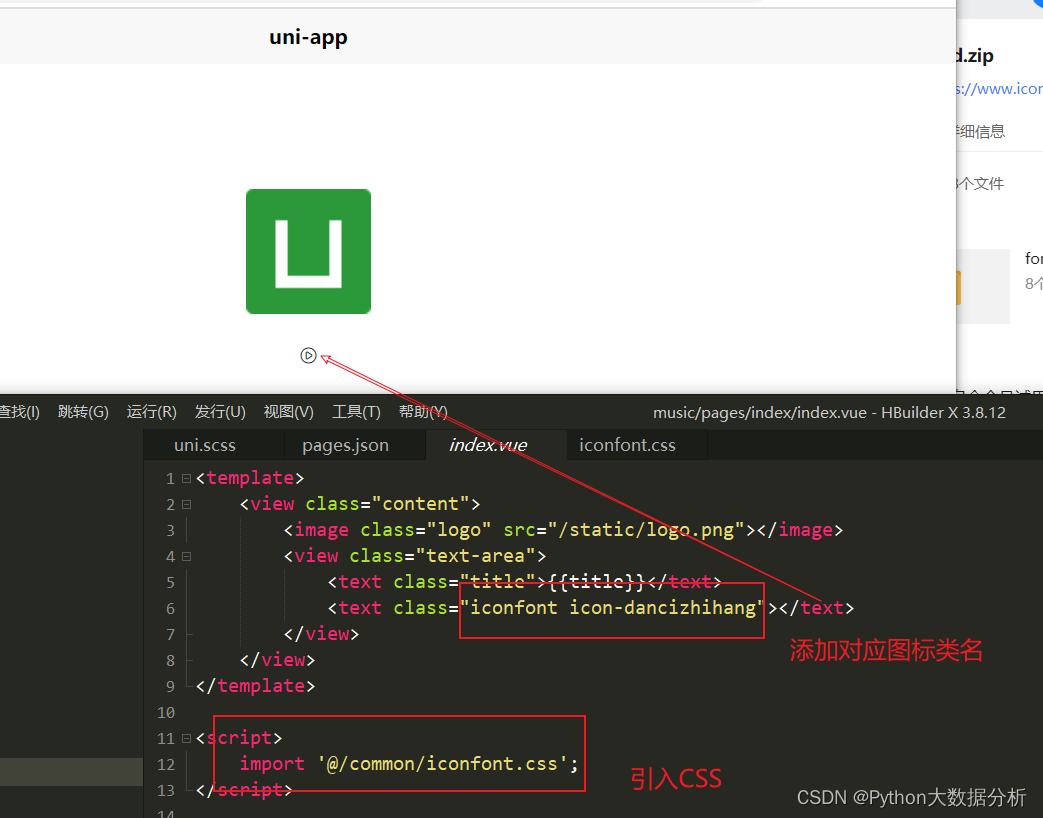
uniapp配置添加阿里巴巴图标icon流程步骤
文章目录 下载复制文件到项目文件夹里项目配置目录结构显示图标 下载 阿里巴巴icon官网 https://www.iconfont.cn/ 复制文件到项目文件夹里 项目配置目录结构 显示图标...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
