【算法题】2 的 n 次幂的背后
前言: 说实话,真的不爱写算法题相关的文章了,觉得没啥意义,但是对这种比较好玩并且简单,学会了就能很好提高算法效率的文章,还是要写一写,不哭不哭,你不会不是你的错,只是因为你懒,学会了就好了,加油!!
一、2 的 n 次幂的特点
我们先看看 2 的 n 次幂都有什么 ?
| n | 2 的 n 次幂 | 二进制表示 |
|---|---|---|
| 1 | 2 | 10 |
| 2 | 4 | 100 |
| 3 | 8 | 1000 |
| 4 | 16 | 10000 |
| … | … | … |
通过观察,我们可以得出,2 的 n 次幂的二进制表示只有最高位是 1, 其余位都是 0,这也是 2 的 n 次幂的特点 。
二、如何判断某个数 x 是否是 2 的 n 次幂
1. 暴力法
对 x 一直除 2 取余数 % , 看看最后当 x == 0 时,余数是否为 0 ,若是为 0 ,说明其是 2 的 n 次幂
2. 利用 2 的 n 次幂的二进制特点
2 的 n 次幂的二进制表示只有最高位为 1,其余位都为 0。因此,我们对其减 1 得到的结果的二进制表示只有原二进制最高位为 0, 其余位都为 1。如下表所示:
| n | 2 的 n 次幂 (x) | 二进制表示 | (x-1) 的二进制表示 | x & (x-1) |
|---|---|---|---|---|
| 1 | 2 | 10 | 01 | 0 |
| 2 | 4 | 100 | 011 | 0 |
| 3 | 8 | 1000 | 0111 | 0 |
| 4 | 16 | 10000 | 01111 | 0 |
| … | … | … | … | 0 |
因此,我们将 该数字 x 按位与 (x - 1),若是结果为 0 ,说明该数字是 2 的 n 次幂
Java 代码表示如下:
if((x & (x-1)) == 0){// 说明是 2 的幂次return true;}
三、如何找到距离某个数最近的 2 的 n 次幂
1. 暴力法
排除 , 我们就不使用暴力法,就不用,就不用 ~~
2. 重点:以数字的二进制形式进行思考
以数字 5 为例,距离它最近的2的幂次,比5大的有一个,比5小的有一个,5 的二进制表示为 101。
因为 2 的幂次只有最高位为 1,那么问题的关键就在于如何消除最低位的 1,消除的方法为 加上最低位 1xx(xx位置为 k 个 0) ,或者减去最低位的 1xx(xx位置为 k 个 0) 。
我们不断进行消除,最后就一定能得到距离 x 的最近的两个 2 的幂次
得到数字 x 的最低位 1xx(xx位置为 k 个 0) 的方法为 : x & (-x)
理解 x & (-x) 之前,我们先恶补一下计算机基础知识:
以 -5 为例:
1. 把这个负数的绝对值转换为二进制,即求原码 (101)
2. 把原码取反,即求反码 (11111111111111111111111111111010)
3. 把反码加1,即求补码 (11111111111111111111111111111011)
所以, 5 & -5 = 1
解释: 通过上述变化 -5 只有最低位的 1xx(xx位置为 k 个 0) 和 5相同,其余位都变得和 5 不同(即被取反了)
3. 寻找最近位置完整代码
// 得到小于 n 的距离 n 最近的 2 的幂次public int getMinDistance(int n){// 直接就是 2 的 n 次幂if((n & (n - 1)) == 0){return n;}// 最低位的 1int lb = n & (-n);// 我们要通过不断加上减去最低位1,来消除低位的1,从而得到只有最高位为1的2的幂次// 但是我们要的是距离n最近的小于n的幂次,因此取两者的最小值return Math.min(getMinDistance(n + lb), getMinDistance(n - lb));}// 得到大于 n 的距离 n 最近的 2 的幂次public int getMaxDistance(int n){// 直接就是 2 的 n 次幂if((n & (n - 1)) == 0){return n;}// 最低位的 1int lb = n & (-n);// 我们要通过不断加上减去最低位1,来消除低位的1,从而得到只有最高位为1的2的幂次// 但是我们要的是距离n最近的大于n的幂次,因此取两者的最大值return Math.max(getMinDistance(n + lb), getMinDistance(n - lb));}
我们在对上面代码得到的结果,进行一个距离绝对值的判断,就能得到我们要的结果了
纠错: 需要这么绕嘛?
当然不需要,在实际实现时,我们只需要找到 x 的最高位 1 的位置,然后进行两次 1 的左移操作就行了。 (以 5 为例子, 1 << 2 (距离最近的小于 5 的位置),1 << 3 (距离最近的大于 5 的位置))
为了下一道题铺垫才这么做的 (试图为自己被绕进去了找借口,wwwww)
四、如何通过不断加减 2 的 n 次幂使得某个数最终结果为 0,最少操作次数
通过上面的分析,我们可以轻松得出这道综合题的完整代码,如下:
class Solution {// 6365. 将整数减少到零需要的最少操作数// 操作依据 —— 找到距离目标值最近的2的n次幂public int minOperations(int n) {return dfs(n);}public int dfs(int n){// 说明是 2 的幂次if((n & (n-1)) == 0){// 说明是 2 的幂次,最后再处理一次,即减去这个数字return 1;}int lb = n & (-n);// 操作次数 + 1,然后递归得到的新的数字return 1 + Math.min(dfs(n + lb), dfs(n - lb));}
}
相关文章:

【算法题】2 的 n 次幂的背后
前言: 说实话,真的不爱写算法题相关的文章了,觉得没啥意义,但是对这种比较好玩并且简单,学会了就能很好提高算法效率的文章,还是要写一写,不哭不哭,你不会不是你的错,只是…...

【人工智能AI】一、NoSQL 企业级基础入门《NoSQL 企业级基础入门与进阶实战》
写一篇介绍什么是NoSQL的技术文章,分5个章节,每个章节细分到3级目录,重点介绍一下优缺点,适用场景,未来发展趋势等。 一、NoSQL简介 1.1 什么是NoSQL NoSQL(Not only SQL),意思是“…...

Ubuntu安装opencv库3.4.10,并在cmake工程中引入opencv库
Windows下安装不同,Ubuntu安装OpenCV库时,需要事先安装依赖,而且不同OpenCV库所需的依赖可能会有所不同,下面的依赖亲测 3.4.10 和 4.5.5版本的有效,但是4.6以上版本安装可能会报错。 参考链接:https://bl…...
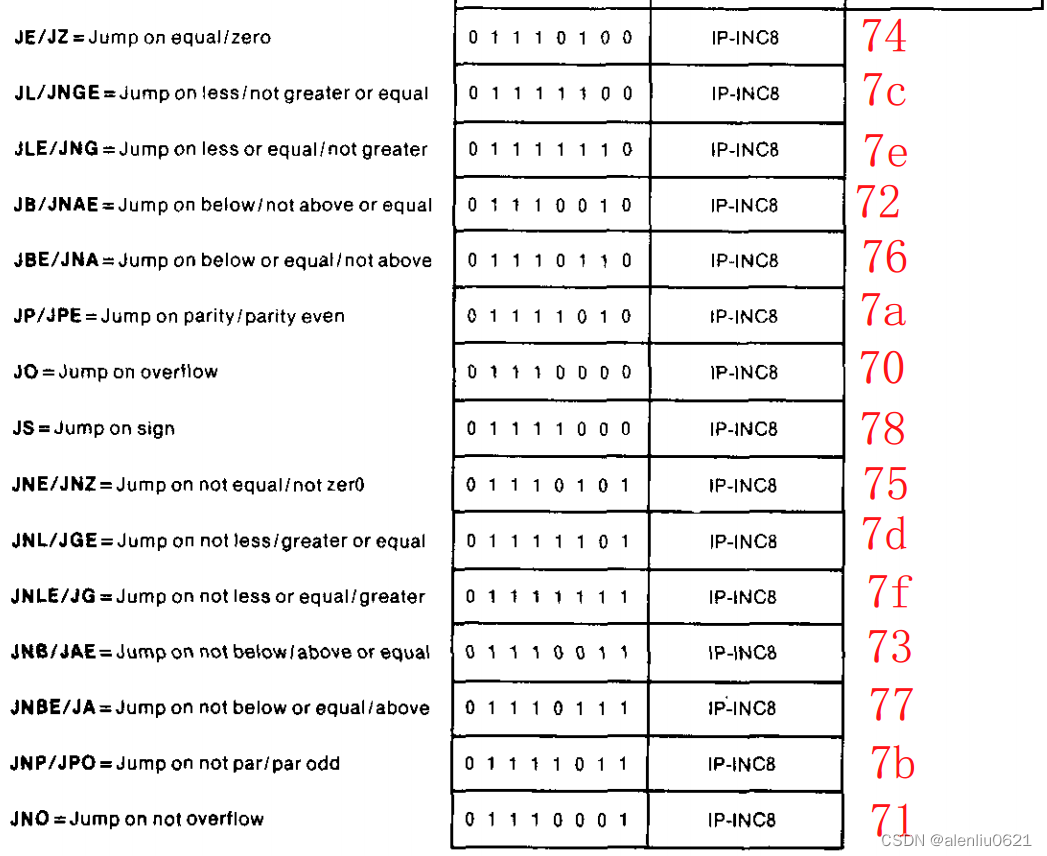
实现8086虚拟机(四)——mov 和 jmp 指令解码
文章目录mov 指令解码jmp 指令解码这篇文章举例来讲讲 mov 指令和 jmp 指令解码函数的实现,其他的指令解码函数都与这些类似。mov 指令解码 以 mov 指令中的一类:寄存器/内存 到/从 寄存器,来详细说明解码函数的实现。 机器指令格式如下&am…...
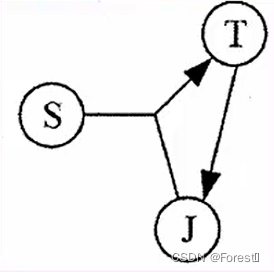
数据库技术-函数依赖、键与约束、范式
一、函数依赖 给定一个x,能唯一确定一个Y,就称x确定Y,或者说Y依赖于x,例如YX*X函数。 函数依赖又可扩展以下两种规则: 部分函数依赖:A可确定C,(A,B)也可确定C,(A,B)中的一部分(即A)可以确定C&a…...
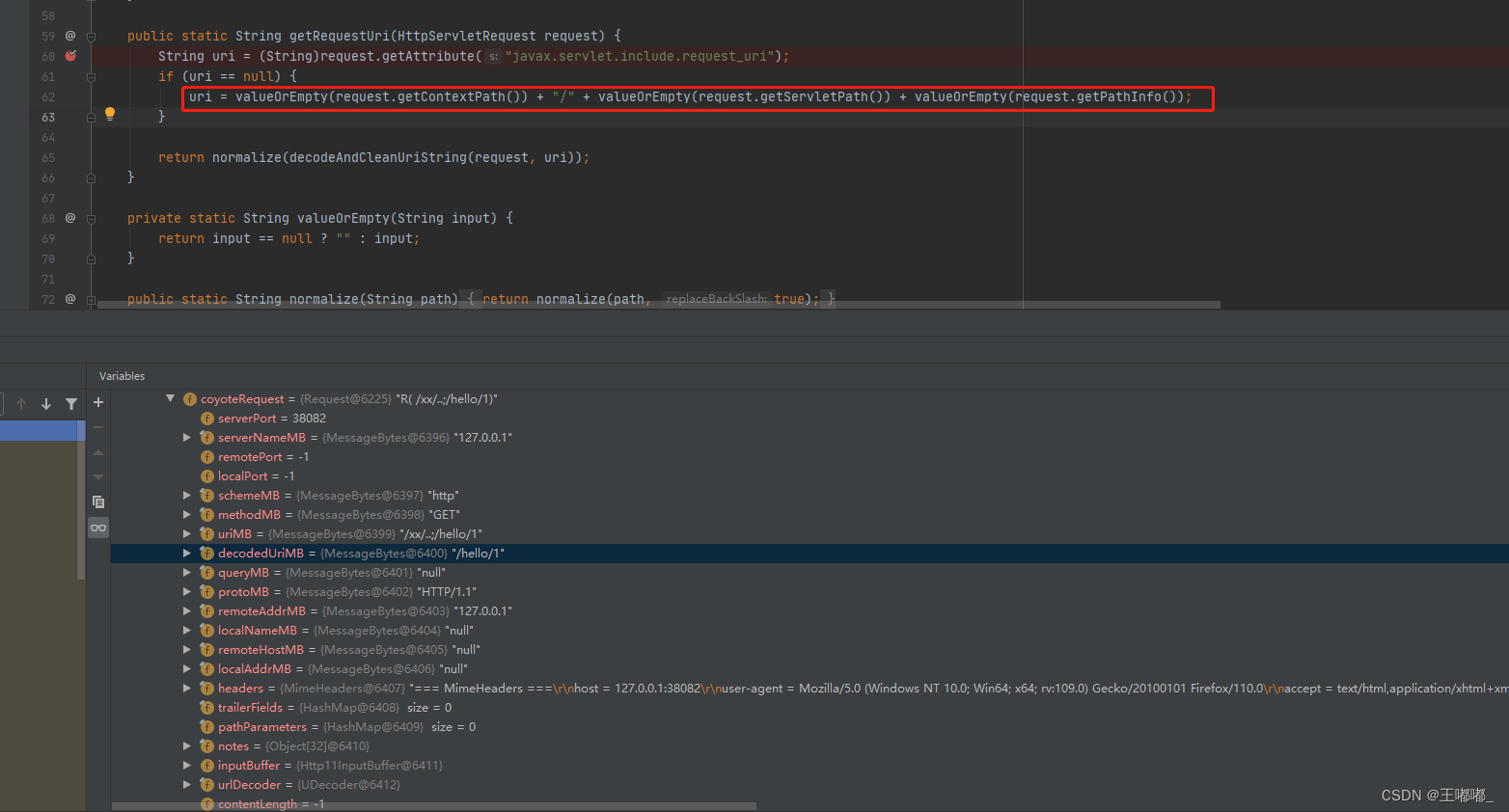
shiro CVE-2020-1957
0x00 前言 在之前只是单纯的复现了漏洞,没有记笔记,所以补充了这篇分析笔记。 影响版本:shiro < 1.5.2 0x01 环境搭建 环境用的是:https://github.com/lenve/javaboy-code-samples/tree/master/shiro/shiro-basic 0x02 漏…...
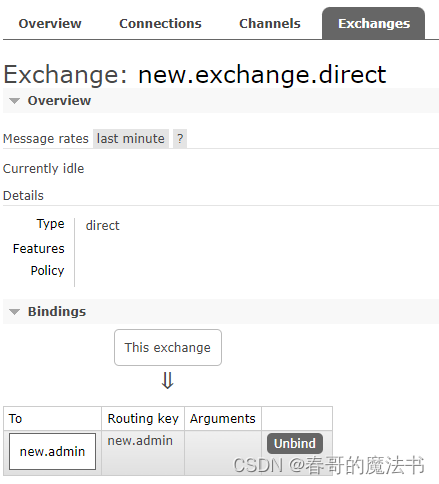
RabbitMQ 入门到应用 ( 五 ) 基本应用
6.更多应用 6.1.AmqpAdmin 工具类 可以通过Spring的Autowired 注入 AmqpAdmin 工具类 , 通过这个工具类创建 队列, 交换机及绑定 import org.springframework.amqp.core.AmqpAdmin; import org.springframework.amqp.core.Binding; import org.springframework.amqp.core.Di…...

部署dapr的辛酸历程
前言dapr大概的了解,个人理解他就是一个分布式服务的管理,把微服务常用的组件(缓存,消息中间件、分布式锁、安全id4等)和监控以及服务注册、发现等等一系列功能以一个很抽象的方式管理起来。可能我们部署微服务用consul、ocelot、polly套件、…...
golang入门笔记——内存管理
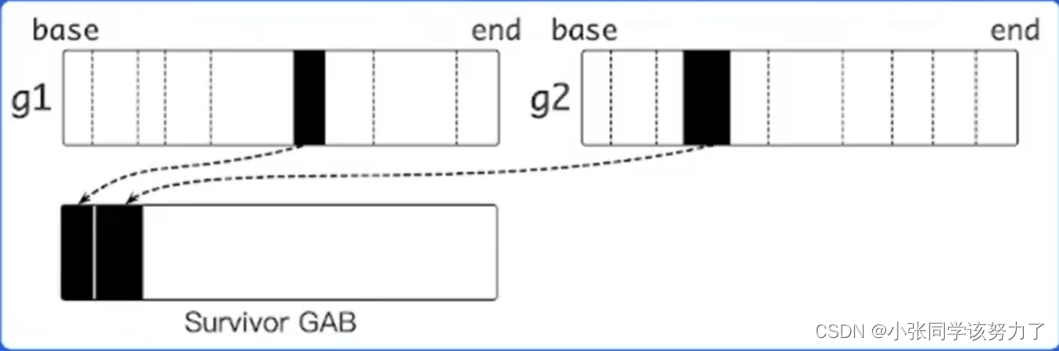
文章目录自动内存管理概念自动内存管理-相关概念:追踪垃圾回收:分代GC(Generational GC)引用计数内存分配Go内存分配-分块Go内存分配——多级缓存Go内存管理优化Balanced GC自动内存管理 概念 1.动态内存 程序在运行时根据需求…...

97. 约数之和
Powered by:NEFU AB-IN Link 文章目录97. 约数之和题意思路代码97. 约数之和 题意 假设现在有两个自然数 A和 B,S是 A^B的所有约数之和。 请你求出 S mod 9901的值是多少。 思路 ABA^BAB的约数之和为:sumAB(1p1p12...p1Ba1)(1p2p22...p2Ba2)...sum_{A^B…...

想和20岁的自己说
男生床头千万不要放卫生纸不要叫自己的女朋友早睡,更不能叫她早起,否则有你好受的。成年人的默契:和异性单独出去旅游,如果没有明确拒绝开一间房,那基本上默认后面会发生的事情不要去考验人性,世上99%的人经…...
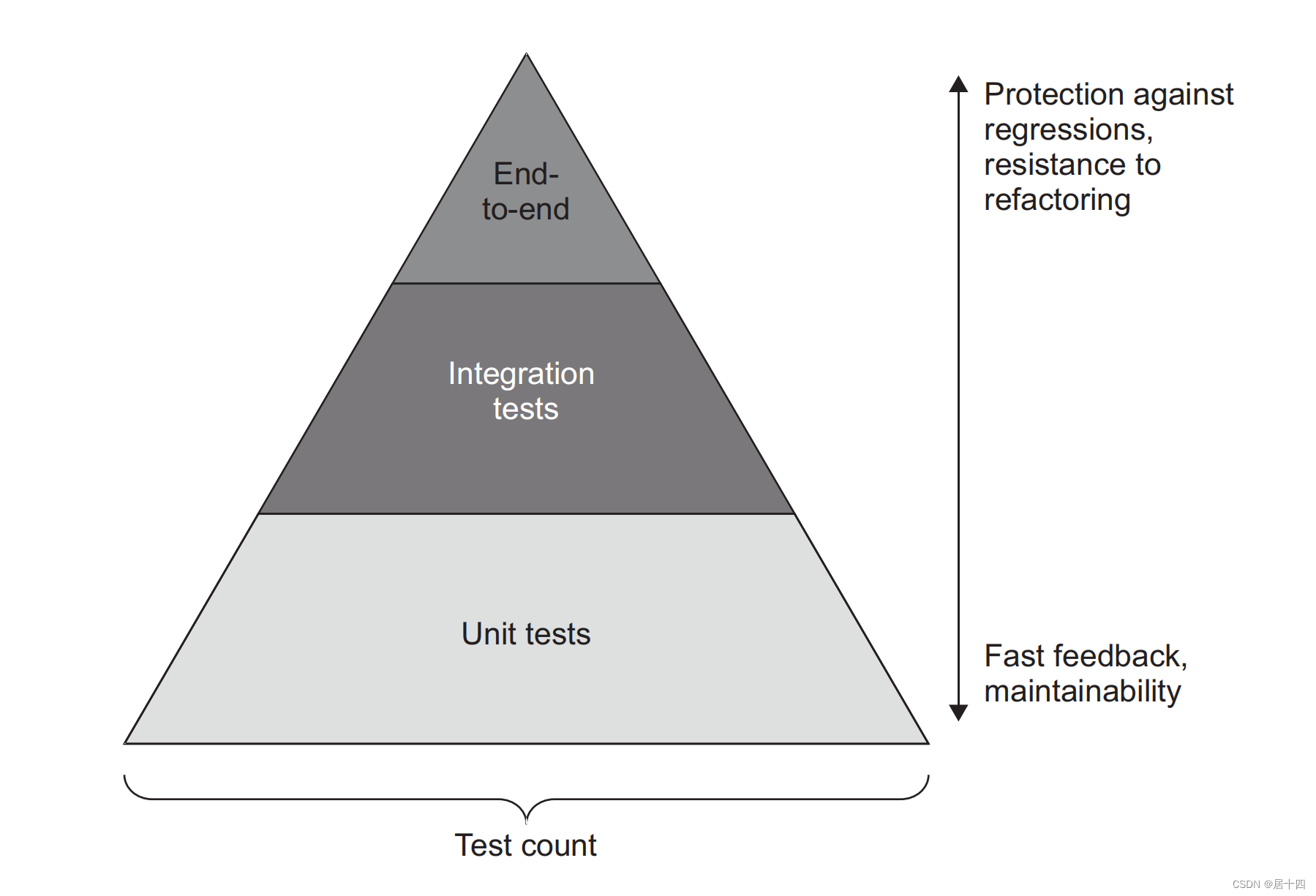
Unit Test and Integration Test
Unit Test and Integration Test Background It is the first time that I try to write an article in English. In the past, I didn’t write test code. Just thinking QA is responsible for testing. As a developer, I don’t need to care about tests. Although I …...

2022年全国职业院校技能大赛(中职组)网络安全竞赛试题(3)
目录 模块A 基础设施设置与安全加固 (本模块20分) 一、项目和任务描述: 假定你是某企业的网络安全工程师,对于企业的服务器系统,根据任务要求确保各服务正常运行,并通过综合运用用户安全管理与密码策略、…...
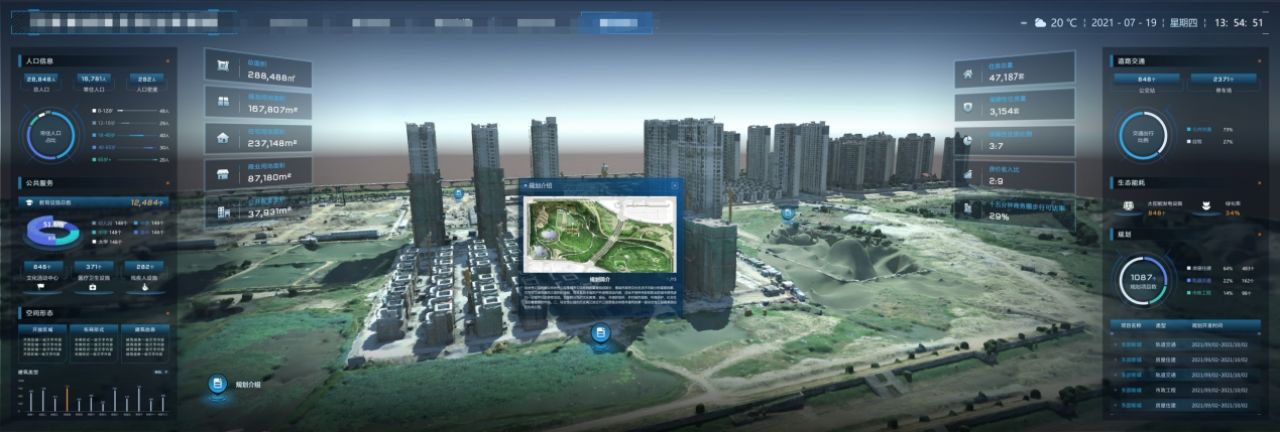
智慧城市应急指挥中心数字化及城市驾驶舱建设方案
目 录 第一章 项目概述 1.1 项目背景 1.2 项目范围 第二章 建设内容 2.1 三维可视化平台 2.1.1 多源数据接入 2.1.2 可视化编排 2.1.3 三维可视化编辑 2.1.4 空间数据可视化 2.1.5 集成框架支持 2.2 可视化场景定制开发 2.2.1 城市驾驶总舱 2.2.2 城市安全分舱 2.…...
HSCSEC 2023 个人练习
😋 大家好,我是YAy_17,是一枚爱好网安的小白。本人水平有限,欢迎各位大佬指点,欢迎关注😁,一起学习 💗 ,一起进步 ⭐ 。⭐ 此后如竟没有炬火,我便是唯一的光。…...
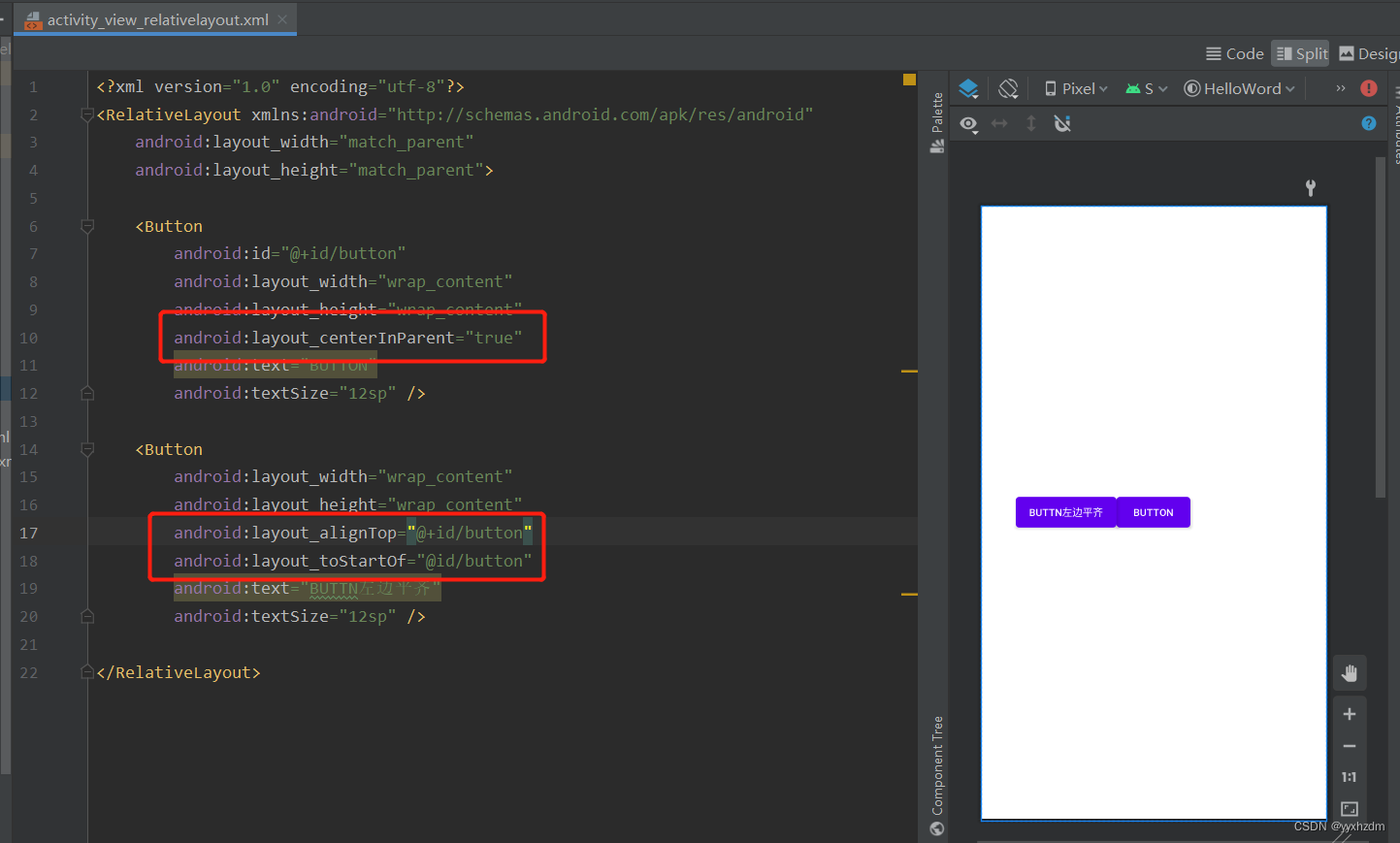
Android 基础知识4-2.7 RelativeLayout(相对布局)
一、RelativeLayout的概述 RelativeLayout(相对布局)是一种根据父容器和兄弟控件作为参照来确定控件位置的布局方式。在很多时候,线性布局还不能满足我们的需求,比如,我们在一行(列)上显示多个控…...

关于云计算,我们问了ChatGPT 10个问题
ChatGPT懂云计算吗?前些天,我们问了ChatGPT(非Plus收费版)一些问题。1. 什么是云计算?2. 云计算行业的护城河是什么?3. 什么是云原生?4. 微软Azure与亚马逊AWS的主要区别是什么?5. 为…...

Netty学习笔记1
Netty学习笔记(一) 在的互联网环境下,分布式系统大行其道,而分布式系统的根基在于网络编程,而 Netty 恰恰是 Java 领域网络编程的王者。如果要致力于开发高性能的服务器程序、高性能的客户端程序,必须掌握…...
)
RISK-V品牌的中国化历程(中)
目录 1.技术优势 出道即巅峰 2.生态布道 品牌根植中国 3.应用场景 加速品牌的商业化运作 生态布道 品牌根植中国 2015年成立非盈利组织RISC-V基金会,目前已吸引全球28个国家327家会员,包括英伟达、联发科、苹果、特斯拉、谷歌、高通、IBM、三星、麻省理…...

2023.02.19 学习周报
文章目录摘要文献阅读1.题目2.摘要3.介绍4.本文贡献5.方法5.1 Local Representation Learning5.2 Global Representation Learning5.3 Item Similarity Gating6.实验6.1 数据集6.2 结果7.结论深度学习1.对偶问题1.1 拉格朗日乘数法1.2 强对偶性2.SVM优化3.软间隔3.1 解决问题3.…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...
