【数据结构】二叉树的链式结构的实现 -- 详解
一、前置说明
在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。为了降低大家学习成本,此处手动快速创建一棵简单的二叉树,快速进入二叉树操作学习。
typedef char BTDataType;typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;// 动态申请一个新节点
BTNode* BuyNode(BTDataType x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));assert(newnode);newnode->data = x;newnode->left = NULL;newnode->right = NULL;return newnode;
}BTNode* CreatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}注意:上述代码并不是创建二叉树的方式。
二、构建二叉树
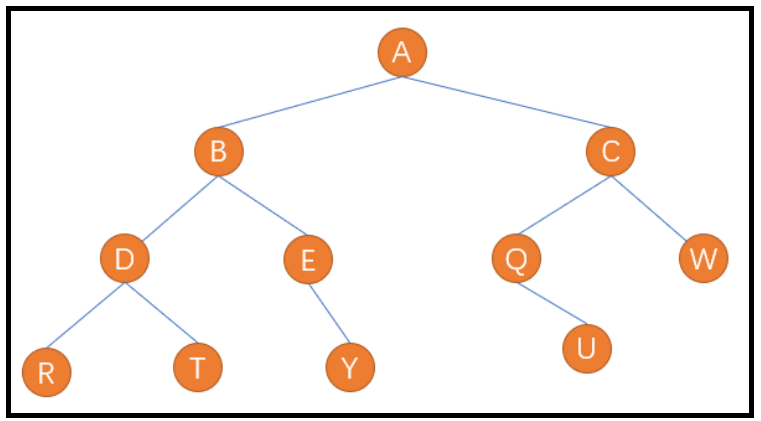
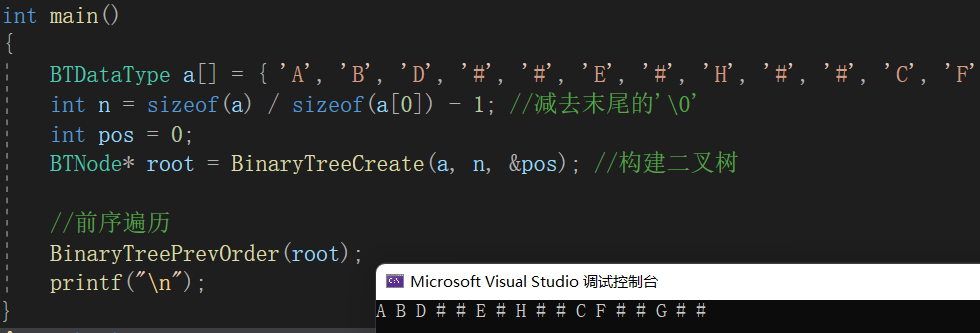
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{if (*pi >= n){return NULL;}char ch = a[*pi];(*pi)++;if (ch == '#'){return NULL;}BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));newNode->data = ch;newNode->left = BinaryTreeCreate(a, n, pi);newNode->right = BinaryTreeCreate(a, n, pi);return newNode;
}
三、二叉树的遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历 (Traversal) 是按照某种特定的规则,依次对二叉 树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
二叉树的遍历方式主要有四种,先介绍三种,最后再介绍第四种。(利用了分治的思想)
- 前序遍历 (Preorder Traversal 亦称先序遍历),方式为先遍历根结点,左子树,右子树。
- 中序遍历 (Inorder Traversal),方式为先遍历左子树,根结点,右子树。
- 后序遍历 (Postorder Traversal),方式为先遍历左子树,右子树,根结点。
// 二叉树前序遍历 void PreOrder(BTNode* root); // 二叉树中序遍历 void InOrder(BTNode* root); // 二叉树后序遍历 void PostOrder(BTNode* root);
其中这三种遍历方式一般都用递归进行实现。
由于被访问的结点必是某子树的根,所以 N(Node)、L(Left subtree)和 R(Right subtree)又可解释为 根、根的左子树和根的右子树。NLR、LNR 和 LRN分别又称为先根遍历、中根遍历和后根遍历。注意 :1️⃣ 深度优先遍厉:前序遍厉、中序遍厉、后序遍厉,注意有些说法只认同前序遍厉。
2️⃣ 广度优先遍厉:层序遍厉。
1、前序遍历
按照前序遍历的方式,我们应该先遍历根结点 A,然后再去遍历左子树。当进入左子树后,我们需要再执行前序遍历方式,即遍历 A 的左子树中的根结点 B,然后再遍历 B 的左子树。当我们再进入左子树,又是先遍历根结点D,然后又遍历左子树,按照顺序遍历到 R,此时终于完成根结点,左子树,接下来遍历右子树。进入右子树后,又遍历根结点T... ...,所以这种遍历方式属于递归性质的。(遍历顺序为:A–>B–>D–>R–>T–>E–>Y–>C–>Q–>U–>W)
// 二叉树前序遍历 void BinaryTreePrevOrder(BTNode* root) // 根->左子树->右子树 {if (root == NULL){printf("# "); // 用#代表NULLreturn;}printf("%c ", root->data);BinaryTreePrevOrder(root->left);BinaryTreePrevOrder(root->right); }
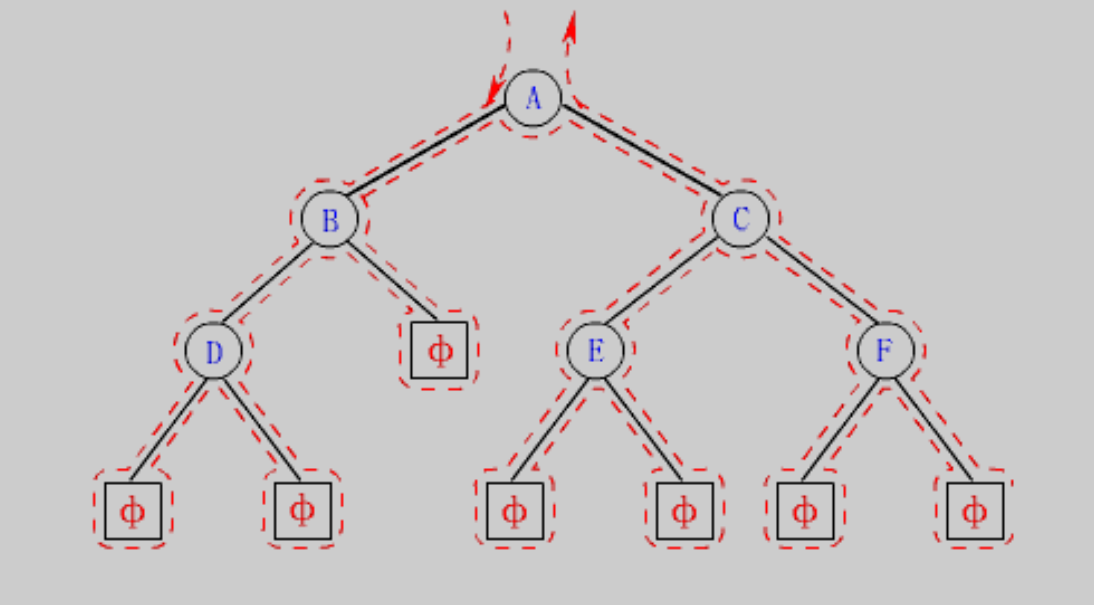
【递归图解】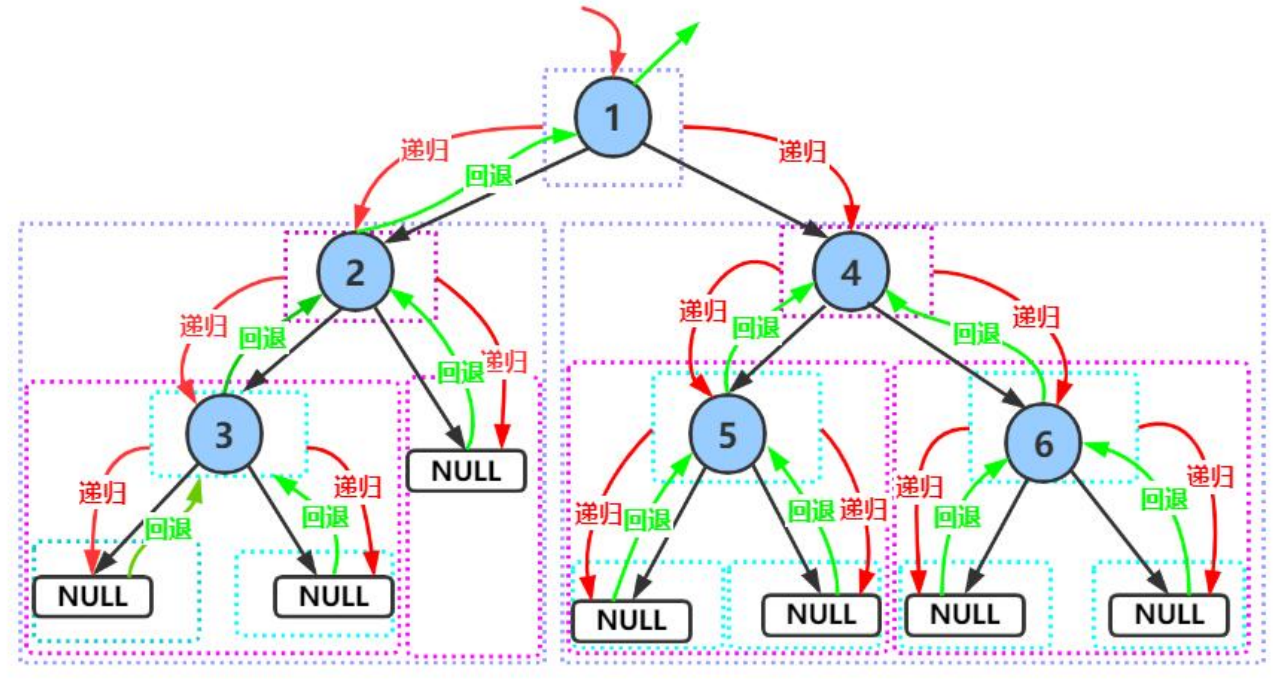
2、中序遍历
中序遍历方式为左子树,根结点,右子树。仍以上面的图为例,遍历顺序为:
R–>D–>T–>B–>E–>Y–>A–>Q–>U–>C–>W
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)// 左子树->根->右子树
{if (root == NULL){printf("# ");return;}BinaryTreeInOrder(root->left);printf("%c ", root->data);BinaryTreeInOrder(root->right);
}3、后序遍历
后序遍历方式为 左子树,右子树,根结点。仍以上面的图为例,遍历顺序应该为:
R–>T–>D–>Y–>E–>B–>U–>Q–>W–>C–>A
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root) // 左子树->右子树->根
{if (root == NULL){printf("# ");return;}BinaryTreePostOrder(root->left);BinaryTreePostOrder(root->right);printf("%c ", root->data);
}【总结】
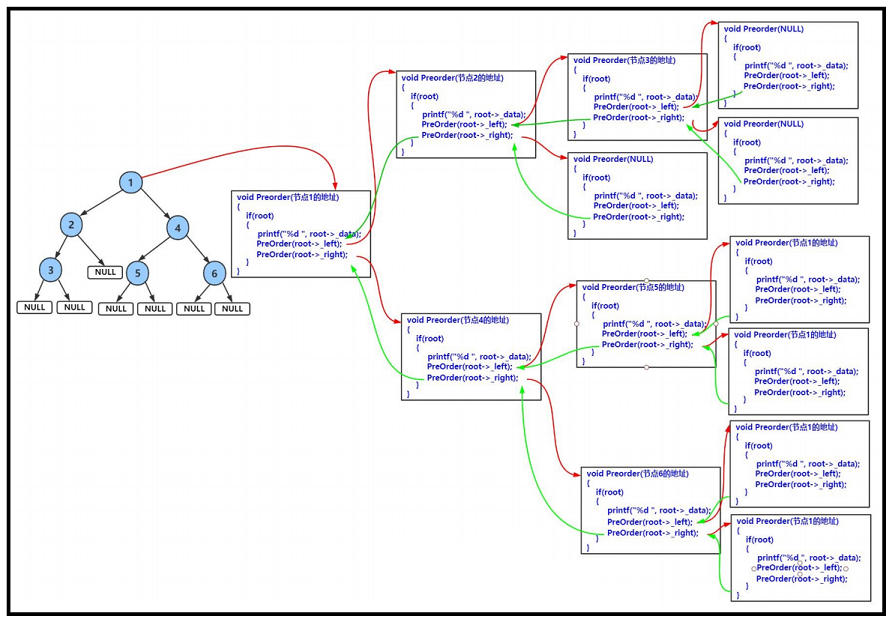
- 前序遍历结果:1->2->3->4->5->6
- 中序遍历结果:3->2->1->5->4->6
- 后序遍历结果:3->2->5->6->4->1
4、层序遍历
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为 1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第 2 层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
// 层序遍历 void LevelOrder(BTNode* root);
注意:层序遍历一般需要使用队列。 (队列内容前面已经详细介绍过了)
【思路】先让根入队列,然后再让根出队列,当左子树不为 NULL 时让左子树入队列,当右子树不为NULL时让右子树入队列,然后不断地迭代下去,直至队列为空。记得出队列前要保存当前值来访问到该元素,Pop 到队列当中的值是地址,通过该地址来访问其中的 data。
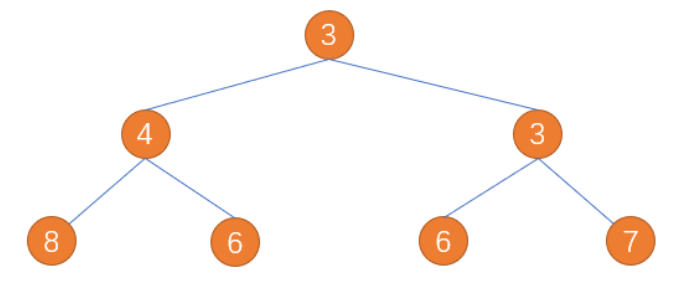
层序遍历结果为: 3->4->3->8->6->6->7
我们该如何利用队列实现呢?
- 判断当前队列是否为空。
- 队列为空:结束;队列非空:取出队列第一个元素入队列。
- 上一层出来后,再入下一层(即它的左右孩子节点)。
由于前面已经对队列的各种操作进行了详解,这里就不展开讲了。(直接运用之前写的 Queue.c 和 Queue.h)
// 层序遍历
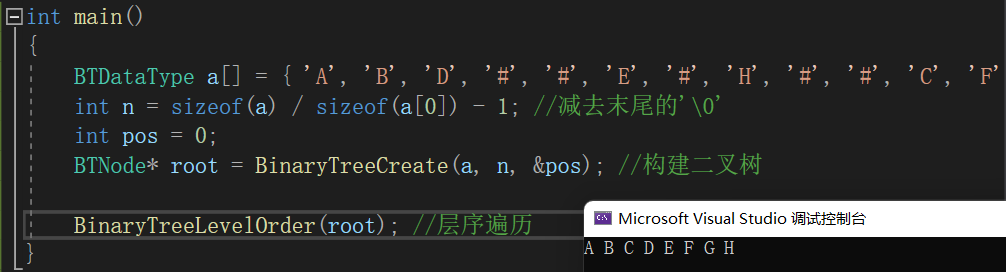
void BinaryTreeLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root) // 树的根节点root不为空 将根节点入队列{QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q); // 获取队列头部元素printf("%c ", front->data); // 打印节点值QueuePop(&q); // 出队列// 如果当前树根的左右孩子不为空 则分别入队列if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}}printf("\n");QueueDestroy(&q);
}
四、二叉树其它接口的实现
1、二叉树的节点个数
按照递归的思想,计算二叉树的节点数量,我们可以认为 二叉树的节点个数 = 左子树数量 + 右子树数量 + 1,其中 1 是当前根节点数量(前提条件是存在根节点)。
⚪【思想 1】
迭代,使用栈来模拟递归的过程,用全局变量 / 静态局部变量来记录节点个数,遍历二叉树的所有节点,并累加节点的个数。
⚪【思想 2】
递归,利用分治的思想,函数使用带返回值的方式,其内部的递归本质上是一个后序遍厉(左子树->右子树->根节点)。
// 二叉树节点个数
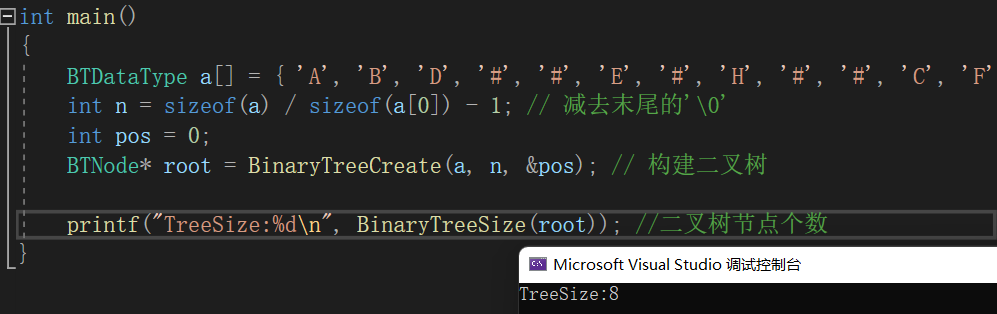
int BinaryTreeSize(BTNode* root)
{return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
2、二叉树叶子节点个数
按照递归的思想,计算二叉树的叶子节点数量,我们可以认为 叶子节点个数 = 左子树叶子节点个数 + 右子树叶子节点个数 + 0,0 是因为当前根结点有子树,说明根结点不是叶子结点。
⚪【思想】
以 left 和 right 为标志,如果都为 NULL,则说明该节点是叶子节点。
// 二叉树叶子节点个数
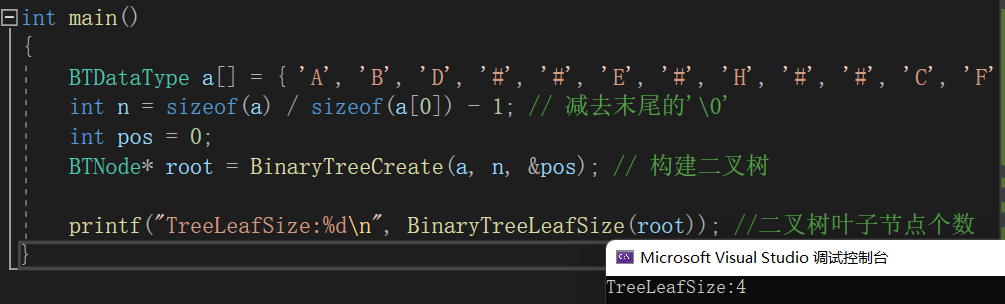
int BinaryTreeLeafSize(BTNode* root)
{// 先判断当前访问的节点是否为空if (root == NULL) {return 0;}// 当前节点不为空,它的左右孩子都为空,说明该节点是叶子节点if (root->left == NULL && root->right == NULL){return 1;}// 当前节点不为空,左右孩子不都为空,则继续往下遍历return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
3、二叉树第k层节点个数
⚪【思想】
求当前树的第 k 层节点个数 = 左子树的第 k-1 层节点个数 + 右子树的第 k-1 层节点个数 (当 k=1 时,说明此层就是目标层)
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{assert(k >= 1);if (root == NULL) // 先判断当前访问的节点是否为空{return 0;}if (k == 1) // 当前节点不为空,而k已经减到1了,说明遍历到了第k层,说明该节点是第k层的{return 1;}// 还没有遍历到第k层,我们就继续往下遍历return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}如何知道这个节点是不是第 k 层的?
求二叉树第 k 层的节点个数,我们从根节点开始往下遍历(按根->左->右的顺序),每遍历一次 k 就减 1一次,当 k==1 时,说明我们遍历到了第 k 层,此时访问该层的节点。如果它不为空,则二叉树第 k 层的节点个数就要 +1。
4、二叉树查找值为x的节点
⚪【思想】
按照递归思想,先判断当前结点是否是目标节点,然后查找左子树,再查找右子树。
如果左右子树都没有找到,就返回NULL。
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL) // 先判断当前访问的节点是否为空{return NULL;}if (root->data == x) // 判断要找的x值节点是不是当前节点{return root;}// 不是当前节点,则继续去该节点的左子树中找BTNode* ret1 = BinaryTreeFind(root->left, x);if (ret1){return ret1;}// 还没找到,再继续去该节点的右子树中找BTNode* ret2 = BinaryTreeFind(root->right, x);if (ret2){return ret2;}return NULL; // 当前节点及其左右子树中都没找到,返回NULL
}5、销毁二叉树
// 二叉树销毁
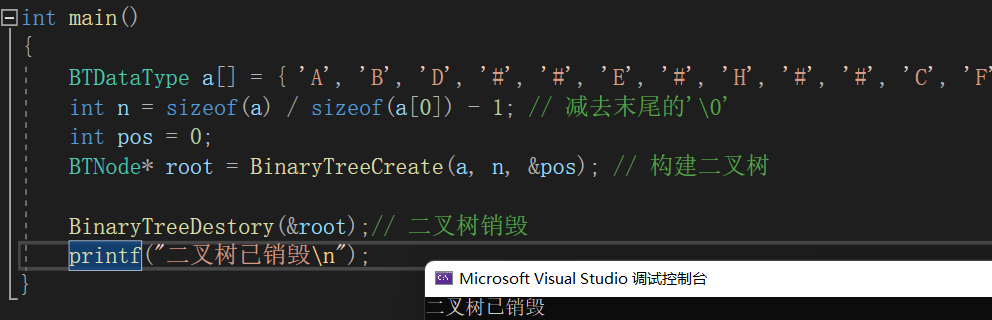
void BinaryTreeDestory(BTNode** root)
{// 如果使用前中序遍历销毁,节点会先被销毁,变成随机值,就不知道它的左右子树位置了 所以采用后序遍历销毁if (*root == NULL){return;}BinaryTreeDestory(&((*root)->left));BinaryTreeDestory(&((*root)->right));free(*root);*root = NULL; // 将根节点设置为NULL 防止野指针
}
注意:如果这里使用前序遍历或中序遍历进行销毁,节点会先被销毁,变成随机值,就不知道它的左右子树位置了,所以应该采用后序遍历来销毁二叉树。
如果这里传进来的是一级指针,由于要在函数内改变形参的值,无法改变外部实参的值,所以我们需要在函数外置头节点指针为NULL。
6、判断二叉树是否是完全二叉树
⚪【思想】
层序遍历时,把空节点也入队列。
- 完全二叉树中,非空节点是连续的,则空节点是连续的。
- 非完全二叉树中,非空节点不是连续的,则空节点不是连续的。
所以在出队时,判断一下,出到第一个空节点时,跳出循环;
在下面重新写一个循环继续出队,并检查出队元素:
- 如果第一个空节点后面的全是空节点,说明是完全二叉树。
- 如果第一个空节点后面的有非空节点,说明是非完全二叉树。
// 判断二叉树是否是完全二叉树(利用层序遍历的思想来判断)
int BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root) // 树的根节点root不为空 将根节点入队列{QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q); // 获取队列头部元素QueuePop(&q); //出队列if (front){// 不管当前树根的左右孩子是否为空,都分别入队列QueuePush(&q, front->left);QueuePush(&q, front->right);}else{break; //遇到空后,跳出层序遍历}}// 如果后面全是空,则是完全二叉树,否则不是完全二叉树while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true; // 出队的节点中,如果没有出现非空节点,说明是完全二叉树出队的节点中,如果没有出现非空节点,说明是完全二叉树
}
五、代码整合
1、Queue.h
// Queue.h
#pragma once#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>struct BinaryTreeNode;typedef struct BinaryTreeNode* QDataType;typedef struct QueueNode
{struct QueueNode* next;QDataType data;
}QNode;typedef struct Queue
{QNode* head;QNode* tail;
}Queue;void QueueInit(Queue* pq);
void QueueDestroy(Queue* pq);
void QueuePush(Queue* pq, QDataType x);
void QueuePop(Queue* pq);
QDataType QueueFront(Queue* pq);
QDataType QueueBack(Queue* pq);
int QueueSize(Queue* pq);
bool QueueEmpty(Queue* pq);2、Queue.c
// Queue.c
#define _CRT_SECURE_NO_WARNINGS 1#include "Queue.h"void QueueInit(Queue* pq)
{assert(pq);pq->head = pq->tail = NULL;
}void QueueDestroy(Queue* pq)
{assert(pq);QNode* cur = pq->head;while (cur){QNode* next = cur->next;free(cur);cur = next;}pq->head = pq->tail = NULL;
}void QueuePush(Queue* pq, QDataType x)
{assert(pq);QNode* newnode = (QNode*)malloc(sizeof(QNode));newnode->data = x;newnode->next = NULL;if (pq->head == NULL){pq->head = pq->tail = newnode;}else{pq->tail->next = newnode;pq->tail = newnode;}
}void QueuePop(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));QNode* next = pq->head->next;free(pq->head);pq->head = next;if (pq->head == NULL){pq->tail = NULL;}
}QDataType QueueFront(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->head->data;
}QDataType QueueBack(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->tail->data;
}int QueueSize(Queue* pq)
{assert(pq);int n = 0;QNode* cur = pq->head;while (cur){++n;cur = cur->next;}return n;
}bool QueueEmpty(Queue* pq)
{assert(pq);return pq->head == NULL;
}3、test.c
// test.c
#define _CRT_SECURE_NO_WARNINGS 1#include "Queue.h"typedef char BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;//动态申请一个新节点
BTNode* BuyNode(BTDataType x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));assert(newnode);newnode->data = x;newnode->left = NULL;newnode->right = NULL;return newnode;
}// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{if (*pi >= n){return NULL;}char ch = a[*pi];(*pi)++;if (ch == '#'){return NULL;}BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));newNode->data = ch;newNode->left = BinaryTreeCreate(a, n, pi);newNode->right = BinaryTreeCreate(a, n, pi);return newNode;
}// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{// 先判断当前访问的节点是否为空if (root == NULL) {return 0;}// 当前节点不为空,它的左右孩子都为空,说明该节点是叶子节点if (root->left == NULL && root->right == NULL){return 1;}// 当前节点不为空,左右孩子不都为空,则继续往下遍历return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{assert(k >= 1);if (root == NULL) // 先判断当前访问的节点是否为空{return 0;}if (k == 1) // 当前节点不为空,而k已经减到1了,说明遍历到了第k层,说明该节点是第k层的{return 1;}// 还没有遍历到第k层,我们就继续往下遍历return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL) // 先判断当前访问的节点是否为空{return NULL;}if (root->data == x) // 判断要找的x值节点是不是当前节点{return root;}// 不是当前节点,则继续去该节点的左子树中找BTNode* ret1 = BinaryTreeFind(root->left, x);if (ret1){return ret1;}// 还没找到,再继续去该节点的右子树中找BTNode* ret2 = BinaryTreeFind(root->right, x);if (ret2){return ret2;}return NULL; // 当前节点及其左右子树中都没找到,返回NULL
}// 二叉树销毁
void BinaryTreeDestory(BTNode** root)
{// 如果使用前中序遍历销毁,节点会先被销毁,变成随机值,就不知道它的左右子树位置了 所以采用后序遍历销毁if (*root == NULL){return;}BinaryTreeDestory(&((*root)->left));BinaryTreeDestory(&((*root)->right));free(*root);*root = NULL; // 将根节点设置为NULL 防止野指针
}// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root) // 根->左子树->右子树
{if (root == NULL){printf("# "); // 用#代表NULLreturn;}printf("%c ", root->data);BinaryTreePrevOrder(root->left);BinaryTreePrevOrder(root->right);
}// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)// 左子树->根->右子树
{if (root == NULL){printf("# ");return;}BinaryTreeInOrder(root->left);printf("%c ", root->data);BinaryTreeInOrder(root->right);
}// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root) // 左子树->右子树->根
{if (root == NULL){printf("# ");return;}BinaryTreePostOrder(root->left);BinaryTreePostOrder(root->right);printf("%c ", root->data);
}// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root) // 树的根节点root不为空 将根节点入队列{QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q); // 获取队列头部元素printf("%c ", front->data); // 打印节点值QueuePop(&q); // 出队列// 如果当前树根的左右孩子不为空 则分别入队列if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}}printf("\n");QueueDestroy(&q);
}// 判断二叉树是否是完全二叉树(利用层序遍历的思想来判断)
int BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root) // 树的根节点root不为空 将根节点入队列{QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q); // 获取队列头部元素QueuePop(&q); //出队列if (front){// 不管当前树根的左右孩子是否为空,都分别入队列QueuePush(&q, front->left);QueuePush(&q, front->right);}else{break; //遇到空后,跳出层序遍历}}// 如果后面全是空,则是完全二叉树,否则不是完全二叉树while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true; // 出队的节点中,如果没有出现非空节点,说明是完全二叉树出队的节点中,如果没有出现非空节点,说明是完全二叉树
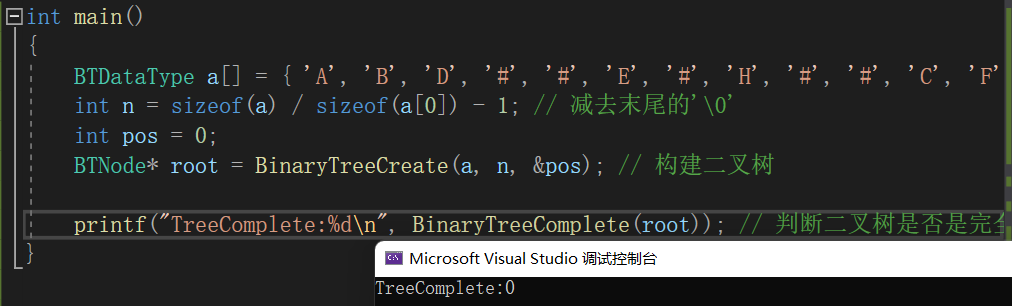
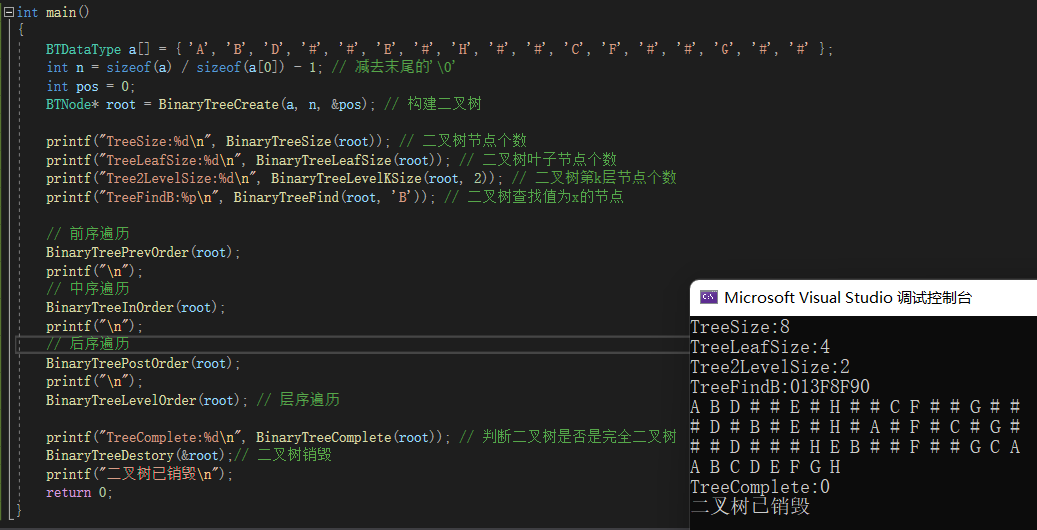
}int main()
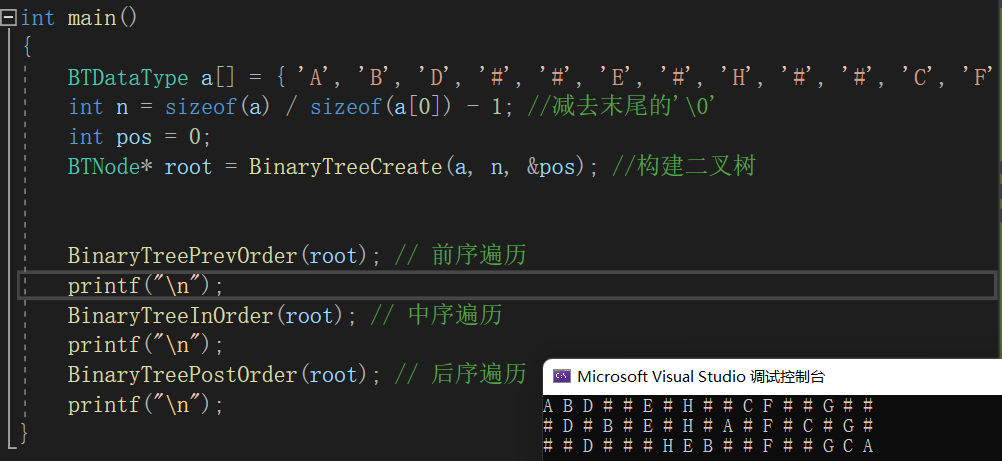
{BTDataType a[] = { 'A', 'B', 'D', '#', '#', 'E', '#', 'H', '#', '#', 'C', 'F', '#', '#', 'G', '#', '#' };int n = sizeof(a) / sizeof(a[0]) - 1; // 减去末尾的'\0'int pos = 0;BTNode* root = BinaryTreeCreate(a, n, &pos); // 构建二叉树printf("TreeSize:%d\n", BinaryTreeSize(root)); // 二叉树节点个数printf("TreeLeafSize:%d\n", BinaryTreeLeafSize(root)); // 二叉树叶子节点个数printf("Tree2LevelSize:%d\n", BinaryTreeLevelKSize(root, 2)); // 二叉树第k层节点个数printf("TreeFindB:%p\n", BinaryTreeFind(root, 'B')); // 二叉树查找值为x的节点// 前序遍历BinaryTreePrevOrder(root);printf("\n");// 中序遍历BinaryTreeInOrder(root);printf("\n");// 后序遍历BinaryTreePostOrder(root);printf("\n");BinaryTreeLevelOrder(root); // 层序遍历printf("TreeComplete:%d\n", BinaryTreeComplete(root)); // 判断二叉树是否是完全二叉树BinaryTreeDestory(&root);// 二叉树销毁printf("二叉树已销毁\n");return 0;
}六、程序运行整体效果
相关文章:

【数据结构】二叉树的链式结构的实现 -- 详解
一、前置说明 在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。为了降低大家学习成本,此处手动快速创建一棵简单的二叉树,快速进入二叉树操作学习。 typedef char BTDataType;typedef struct Binar…...

【C语言】什么是结构体内存对齐?结构体的大小怎么计算?
目录 1.结构体内存对齐 对偏移量的理解: 2.结构体的大小计算 2.1结构体中只有普通的数据类型的大小计算 2.2 结构体中有嵌套的结构体的大小计算 3.修改默认对齐数 4.为什么存在内存对齐? 这篇文章主要介绍结构体内存对齐和如何计算大小。 在学习结构体内存…...

【Redis】Redis中的布隆过滤器
【Redis】Redis中的布隆过滤器 前言 在实际开发中,会遇到很多要判断一个元素是否在某个集合中的业务场景,类似于垃圾邮件的识别,恶意IP地址的访问,缓存穿透等情况。类似于缓存穿透这种情况,有许多的解决方法…...

接口测试 —— Jmeter 参数加密实现
Jmeter有两种方法可以实现算法加密 1、使用__digest自带函数 参数说明: Digest algorithm:算法摘要,可输入值:MD2、MD5、SHA-1、SHA-224、SHA-256、SHA-384、SHA-512 String to be hashed:要加密的数据 Salt to be…...

Linux c语言字节序
文章目录 一、简介二、大小端判断2.1 联合体2.2 指针2.3 网络字节序 一、简介 字节序(Byte Order)指的是在存储和表示多字节数据类型(如整数和浮点数)时,字节的排列顺序。常见的字节序有大端字节序(Big En…...

批量将excel中第5列中内容将人名和电话号码进行分列
使用Python可以使用openpyxl库来实现批量将Excel中第5列的内容分列为人名和电话号码的操作。下面是示例代码: import openpyxl def split_names_and_phone_numbers(file_path, sheet_name): # 加载Excel文件 workbook openpyxl.load_workbook(file_path) …...

WPF DataGrid columns表头根据数据集动态动态生成Demo
思路是这样的,数组集合装表头的信息,遍历这个集合,遍历过程中处理一下数据,然后就把每表头信息添加到dataGrid2.Columns.Add(templateColumn); 1,页面Xaml代码: <DataGrid x:Name"dataGrid" …...
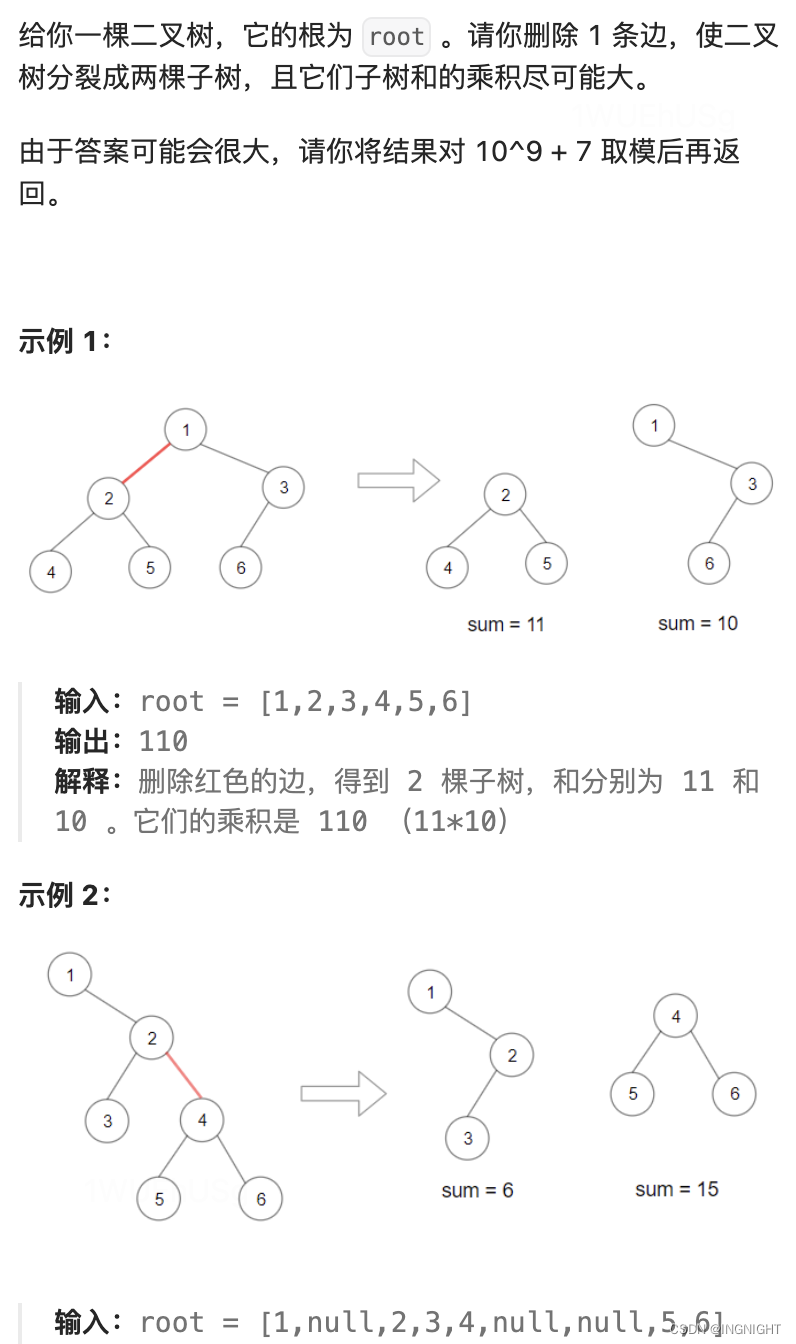
1339. 分裂二叉树的最大乘积
链接: 1339. 分裂二叉树的最大乘积 题解: /*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* …...

【C++】Stack和Queue
欢迎来到Cefler的博客😁 🕌博客主页:那个传说中的man的主页 🏠个人专栏:题目解析 🌎推荐文章:题目大解析3 目录 👉🏻Stack Constructor👉🏻Stack …...

Maven之tomcat7-maven-plugin 版本低的问题
tomcat7-maven-plugin 版本『低』的问题 相较于当前最新版的 tomcat 10 而言,tomcat7-maven-plugin 确实看起来很显老旧。但是,这个问题并不是问题,至少不是大问题。 原因 1:tomcat7-maven-plugin 仅用于我们(程序员&…...
在项目中如何解除idea和Git的绑定
在项目中如何解除idea和Git的绑定 1、点击File--->Settings...(CtrlAltS)--->Version Control--->Directory Mappings--->点击取消Git的注册根路径: 2、回到idea界面就没有Git了: 3、给这个项目初始化 这样就可以重新绑定远程仓库了&#x…...
AGI 在网易云信的技术提效和业务创新
We believe our research will eventually lead to artificial general intelligence, a system that can solve human-level problems. Building safe and beneficial AGI is our mission. ---- OpenAI 通用人工智能 AGI 作为 AI 的终极形态,是 AI 行业内追求的演…...

线性代数的学习和整理9(草稿-----未完成)
3.3 特征值和特征向量是什么? 直接说现在:特征向量这个块往哪个方向进行了拉伸,各个方向拉伸了几倍。这也让人很容易理解为什么,行列式的值就是特征值的乘积。 特征向量也代表了一些良好的性质,即这些线在线性变换后…...

React的useReducer与Reudx对比
useReducer 和 Redux 都是用于处理应用程序的状态管理的工具,但它们在概念和使用场景上存在一些区别。 useReducer: useReducer 是 React 提供的一个 Hook,用于管理局部状态。它接受一个 reducer 函数和初始状态,并返回一个包含当…...
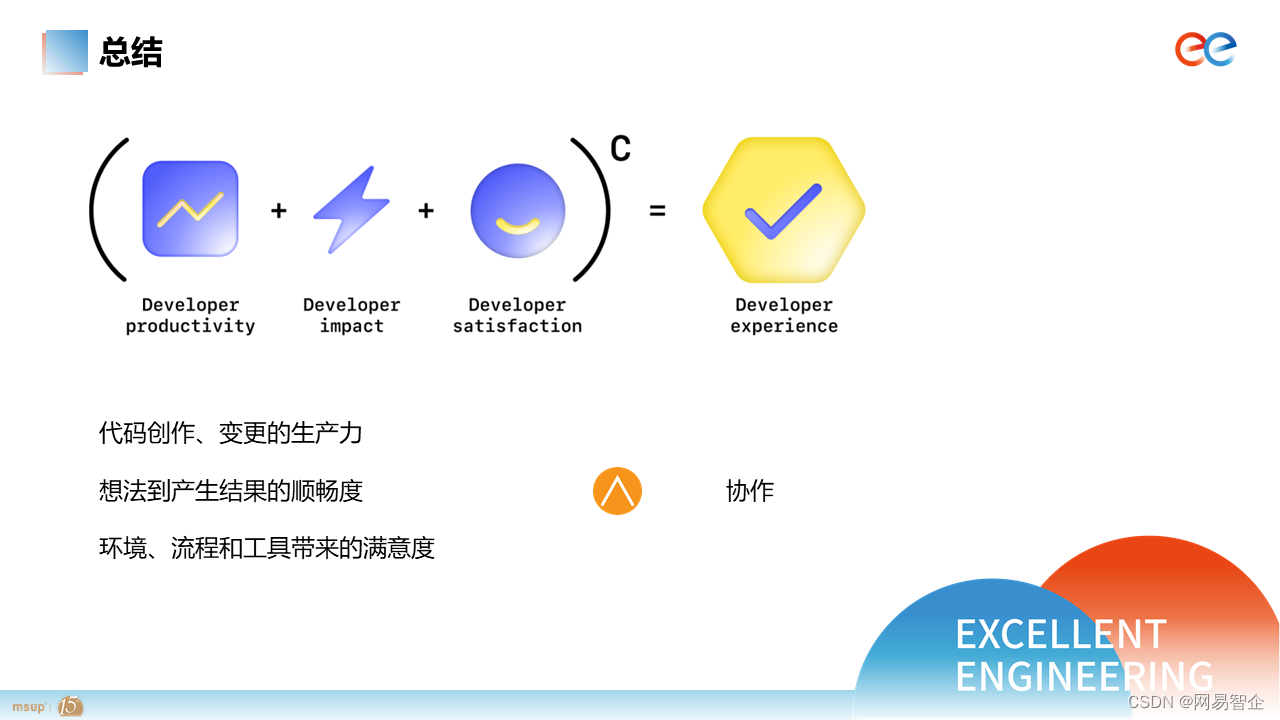
深度学习环境搭建 cuda、模型量化bitsandbytes安装教程 windows、linux
cuda、cudann、conda安装教程 输入以下命令,查看 GPU 支持的最高 CUDA 版本。 nvidia-smi cuda安装(cudatoolkit) 前往 Nvidia 的 CUDA 官网:CUDA Toolkit Archive | NVIDIA Developer CUDA Toolkit 11.8 Downloads | NVIDIA …...

pythond assert 0 <= colx < X12_MAX_COLS AssertionError
python使用xlrd读取excel时,报错: assert 0 < colx < X12_MAX_COLS AssertionError 大意是excel列太多了。主要是xlrd库的问题。最好的方法是不用它,但是我用的其他人提供的工具用到它,没法改。 尝试手动删除excel的列&am…...
js简介以及在html中的2种使用方式(hello world)
简介 javascript :是一个跨平台的脚本语言;是一种轻量级的编程语言。 JavaScript 是 Web 的编程语言。所有现代的 HTML 页面都使用 JavaScript。 HTML: 结构 css: 表现 JS: 行为 HTMLCSS 只能称之为静态网页࿰…...

vsCode使用cuda
一、vsCode使用cuda 前情提要:配置好mingw: 1.安装cuda 参考: **CUDA Toolkit安装教程(Windows):**https://blog.csdn.net/qq_42951560/article/details/116131410 2.在vscode中添加includePath c_cp…...

ubuntu无法使用apt命令时怎么安装库
如题 因为某些原因,不能直接联网使用apt命令安装库。只能手动去ubuntu镜像源里 找对应的包的deb安装文件 镜像源地址(适用于AMD64架构,就是常见的PC的X86-64啦) 镜像源地址(适用于ARM64,armhf,ppc64el,riscv64,s390x架构ÿ…...

防火墙firewall
一、什么是防火墙 二、iptables 1、iptables介绍 2、实验 138的已经被拒绝,1可以 三、firewalld 1、firewalld简介 关闭iptables,开启firewalld,curl不能使用,远程连接ssh可以使用 添加80端口 这样写也可以:添加http…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...