【算法】二分查找(整数二分和浮点数二分)
二分查找也称折半查找(Binary Search),是一种效率较高的查找方法,时间复杂度为O(logN)。
二分查找采用了“分治”策略。使用二分查找时,数组中的元素之间得有单调性(升序或者降序)。
二分的模板据我目前所知有三个,但是下面是我个人认为最好的一种(比较简单,不容易写错~)
1. 整数二分
整数二分过程:
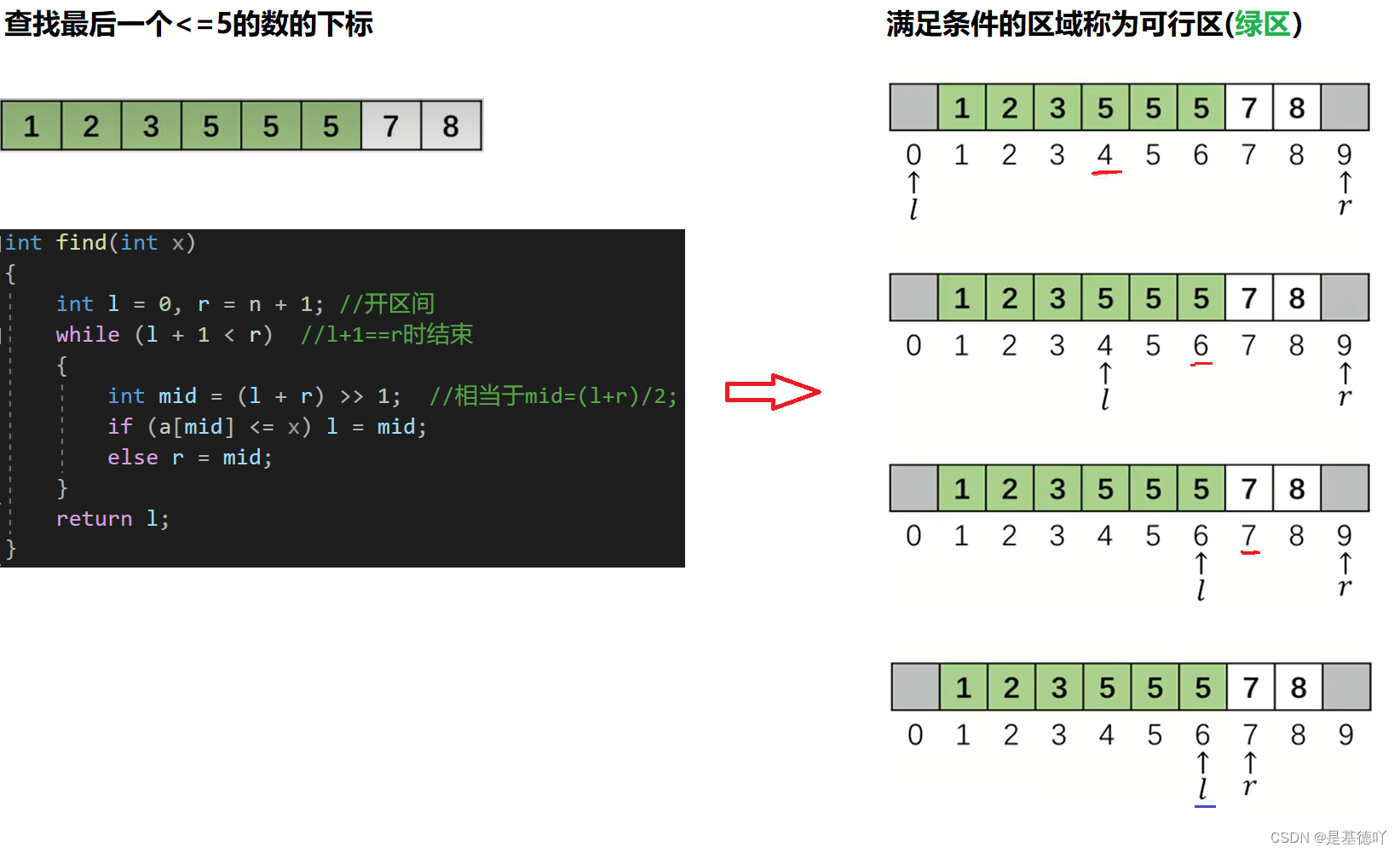
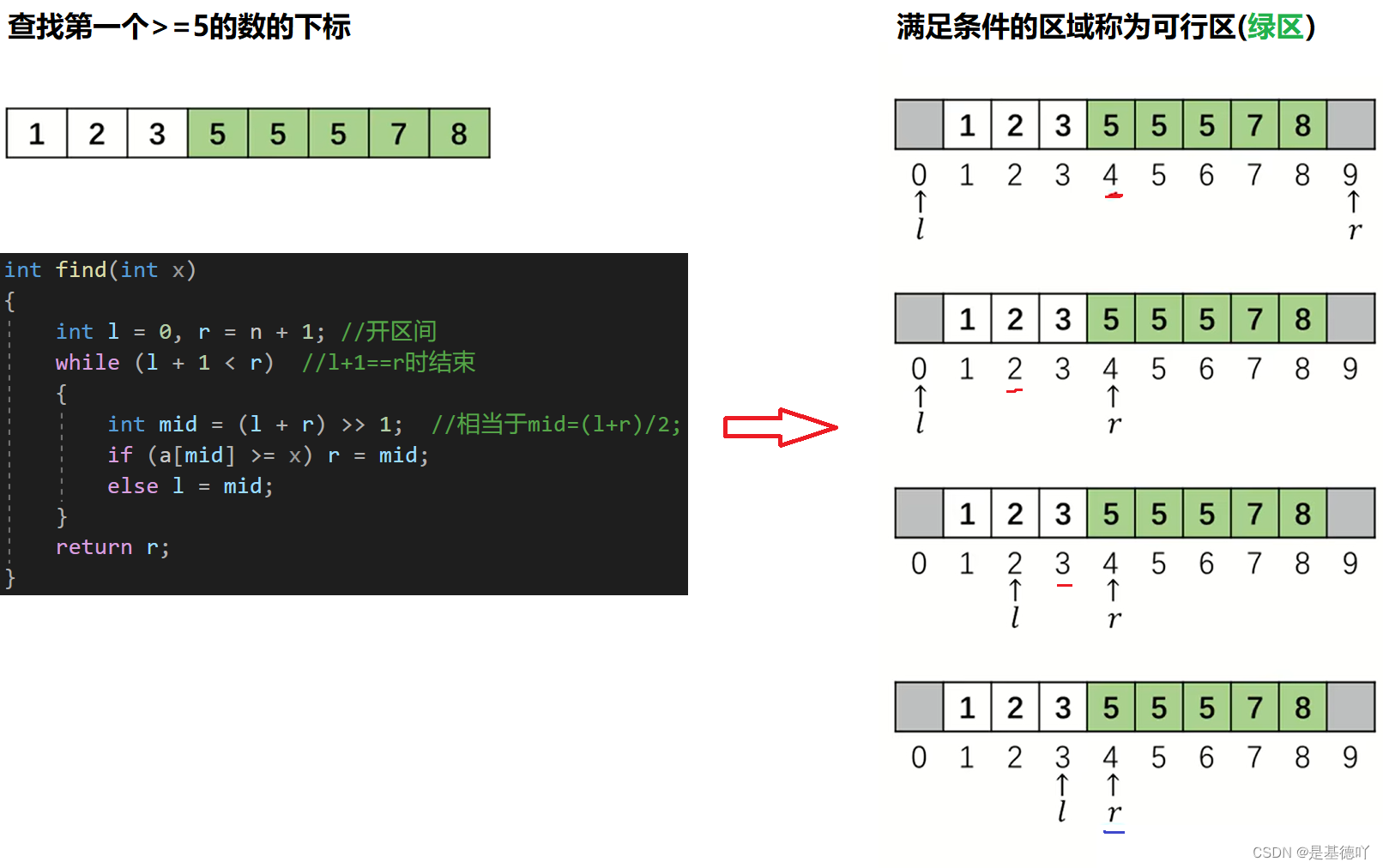
普遍规律:
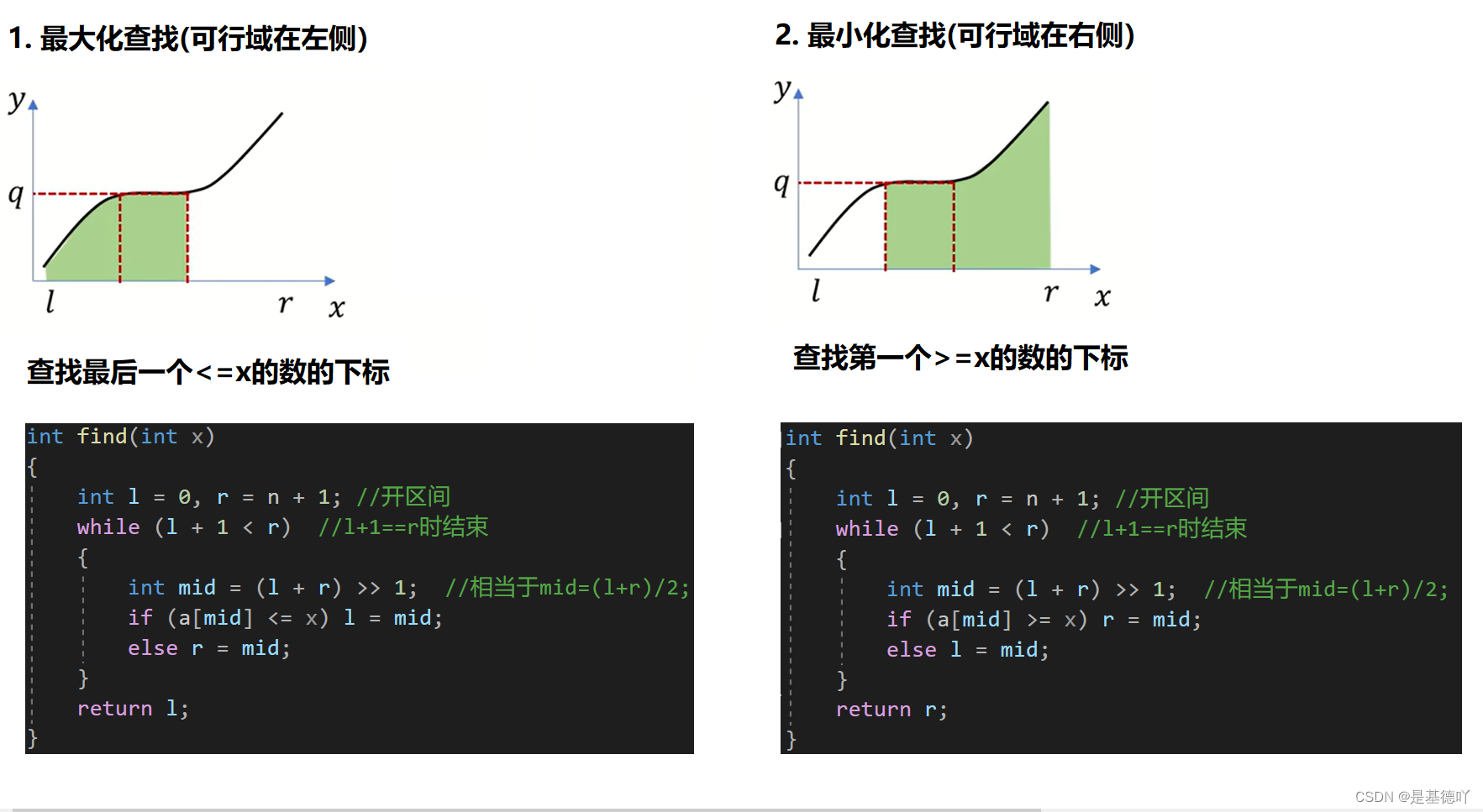
我们发现:

2. 整数二分模板
查找最后一个<=x的数的下标:
int find(int x)
{int l = 0, r = n + 1; //开区间while (l + 1 < r) //l+1==r时结束{int mid = (l + r) >> 1; //相当于mid=(l+r)/2;if (a[mid] <= x) l = mid;else r = mid;}return l;
}查找第一个>=x的数的下标:
int find(int x)
{int l = 0, r = n + 1; //开区间while (l + 1 < r) //l+1==r时结束{int mid = (l + r) >> 1; //相当于mid=(l+r)/2;if (a[mid] >= x) r = mid;else l = mid;}return r;
}3. 整数二分模板题
3.1 洛谷P2249 【深基13.例1】查找
原题链接:https://www.luogu.com.cn/problem/P2249

#define _CRT_SECURE_NO_WARNINGS 1
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int a[N], n, m;
int find(int x)
{int l = 0, r = n + 1;while (l + 1 < r){int mid = (l + r) >> 1;if (a[mid] >= x) r = mid;else l = mid;}if (a[r] == x) return r;else return -1;
}
int main()
{scanf("%d%d", &n, &m);for (int i = 1; i <= n; i++) scanf("%d", &a[i]);while (m--){int k;scanf("%d", &k);printf("%d ", find(k));}return 0;
} 3.2 Acwing789. 数的范围
3.2 Acwing789. 数的范围
原题链接:https://www.acwing.com/problem/content/791/

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int a[N],n,q;
int find1(int x)
{int l=-1,r=n;while(l+1<r){int mid=(l+r)>>1;if(a[mid]>=x) r=mid;else l=mid;}if(a[r]==x) return r;else return -1;
}
int find2(int x)
{int l=-1,r=n;while(l+1<r){int mid=(l+r)>>1;if(a[mid]<=x) l=mid;else r=mid;}if(a[l]==x) return l;else return -1;
}
int main()
{scanf("%d%d",&n,&q);for(int i=0;i<n;i++) scanf("%d",&a[i]);while(q--){int k;scanf("%d",&k);printf("%d %d\n",find1(k),find2(k));}
}4. 浮点数二分
我们看下图:

分析:
(其实是个二分答案的题目)
y=x^3,我们知道这是个单调递增的函数。
-10000开三次方根大概是-27,10000开三次方根大概是27。
因为-10000<=y<=10000,我们为了方便,把左边界设置成-100,右边界设置成100。

我们可以直观看到-27~27包含在-100~100。所以这样设置左右边界是没有问题滴。
我们不断二分缩小范围,当l和r非常接近时(r-l<=1e-8),我们就认为找到了这个三次方根。
否则我们用while(r-l>=1e-8)继续循环遍历。
又因为是递增的,所以mid*mid*mid<=y,我们让区间往右靠(l=mid);反之,当mid*mid*mid>y时,我们让区间往左靠(r=mid)。
最后返回左边界l即可。
5. 浮点数二分模板
double find(double y)
{double l = -100, r = 100;while (r - l > 1e-8){double mid = (l + r) / 2;if (mid * mid * mid <= y) l = mid;else r = mid;}return l;
}6. 浮点数二分模板题
6.1 Acwing 790.数的三次方根
原题链接:https://www.acwing.com/problem/content/792/

#include<bits/stdc++.h>
using namespace std;
double n;
int main()
{scanf("%lf", &n);double l = -100, r = 100;while (r - l > 1e-8){double mid = (l + r) / 2;if (mid * mid * mid <= n) l = mid;else r = mid;}printf("%.6lf\n", r);return 0;
}

相关文章:

【算法】二分查找(整数二分和浮点数二分)
二分查找也称折半查找(Binary Search),是一种效率较高的查找方法,时间复杂度为O(logN)。 二分查找采用了“分治”策略。使用二分查找时,数组中的元素之间得有单调性(升序或者降序)。 二分的模…...
git压缩/合并多次commit提交为1次commit提交
git压缩/合并N次commit提交为1次commit提交 假设有最近3次提交: commit_id1 commit_id2 commit_id3目标是把以上3次commit合并成1个commit,注意,最新的commit提交在最上面。 在git bash里面的操作步骤: (1࿰…...
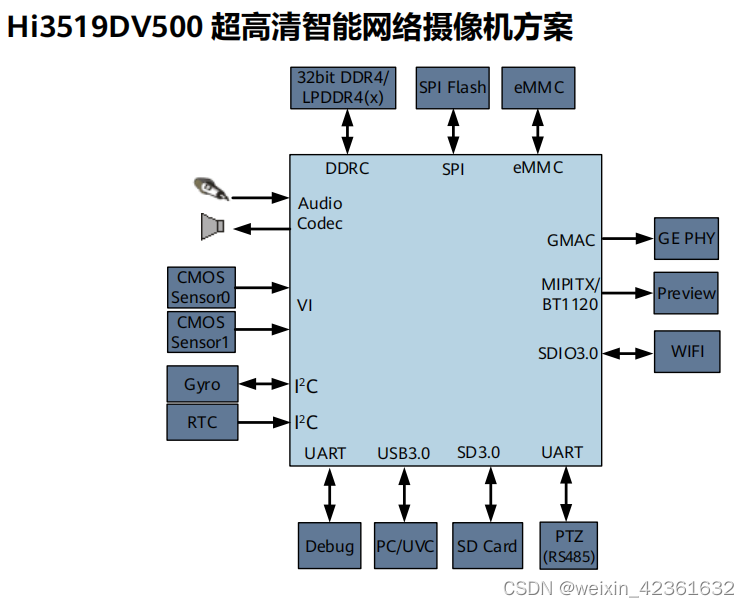
【3519DV500】AI算法承载硬件平台_2.5T算力+AI ISP图像处理_超感光视频硬件方案开发
Hi3519DV500 内置双核 A55 ,提供高效、丰富和灵活的CPU 资源,以满足客户计算和控制需求。 Hi3519DV500集成了高效的神经网络推理引擎,最高2.5Tops NN算力,支持业界主流的神经 网络框架。神经网络支持完整的 API 和工具链…...

Linux系统基础服务启动的方法
服务,其实就是运行在操作系统后台的一个或者多个应用程序,为计算机系统或用户提供某项特定的服务。Linux系统运行的绝大多数服务都是需要安装才有的,例如FTP服务、httpd服务、MySQL、redis、Zookeeper、rabbitmq、vsftpd等等,那么…...
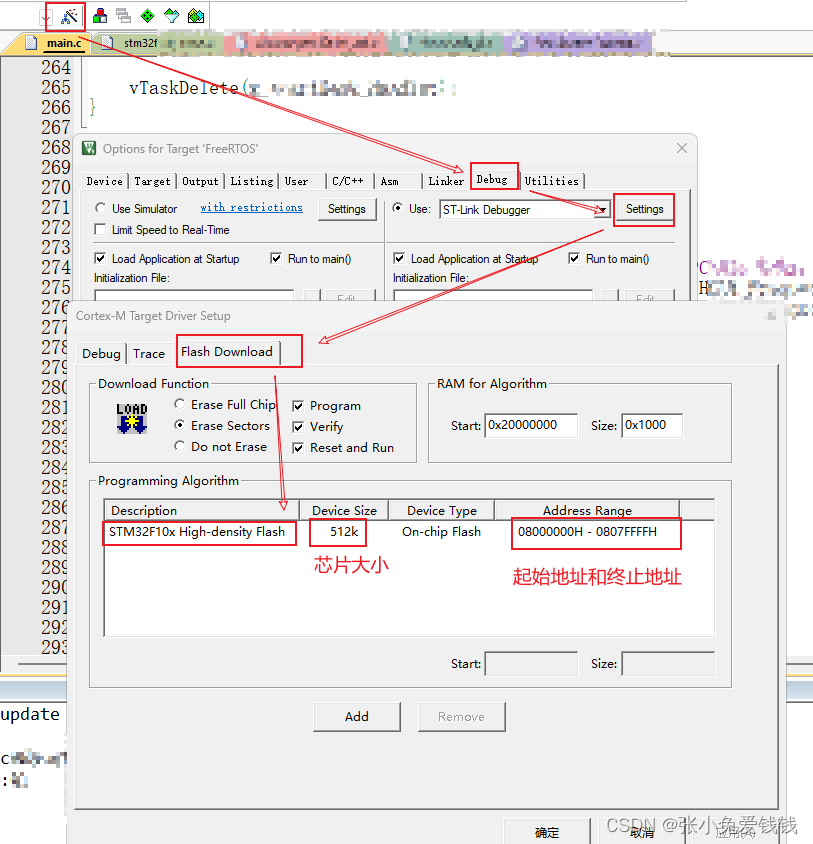
STM32 FLASH 读写数据
1. 《STM32 中文参考手册》,需要查看芯片数据手册,代码起始地址一般都是0x8000 0000,这是存放整个项目代码的起始地址 2. 编译信息查看代码大小,修改代码后第一次编译后会有这个提示信息 2.1 修改代码后编译,会有提示…...
编程笔记--1 初识功能区)
excel功能区(ribbonx)编程笔记--1 初识功能区
再office2003版本以前,excel是具有菜单栏和工具栏的,再office2007及以后的版本中,界面中没有菜单栏和工具栏,使用功能区替换了菜单和工具栏。 您可能意识到自定义用户界面也变得更加困难,其实设置功能区并不会像您想像的那样困难,因为Microsoft也意识到必须有一种方式供开…...
电脑远程接入软件可以进行文件传输吗?快解析内网穿透
电脑远程接入软件的出现,让我们可以在两台电脑之间进行交互和操作。但是,很多人对于这些软件能否进行文件传输还存在一些疑问。下面的文章将解答这个问题。 1.电脑远程接入软件可以进行文件传输。传统上,我们可能会通过传输线或者移动存储设…...
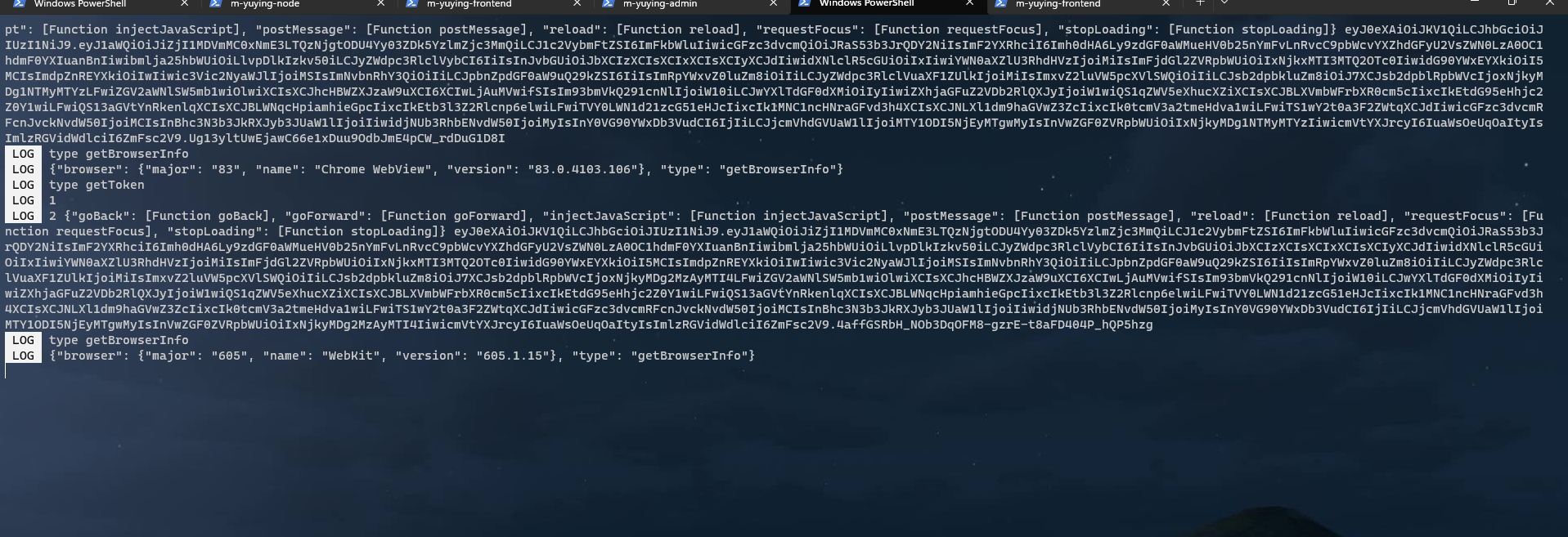
react-native-webview使用postMessage后H5不能监听问题(iOS和安卓的兼容问题)
/* 监听rn消息 */ const eventListener nativeEvent > {//解析数据actionType、extraconst {actionType, extra} nativeEvent.data && JSON.parse(nativeEvent.data) || {} } //安卓用document,ios用window window.addEventListener(message, eventLis…...
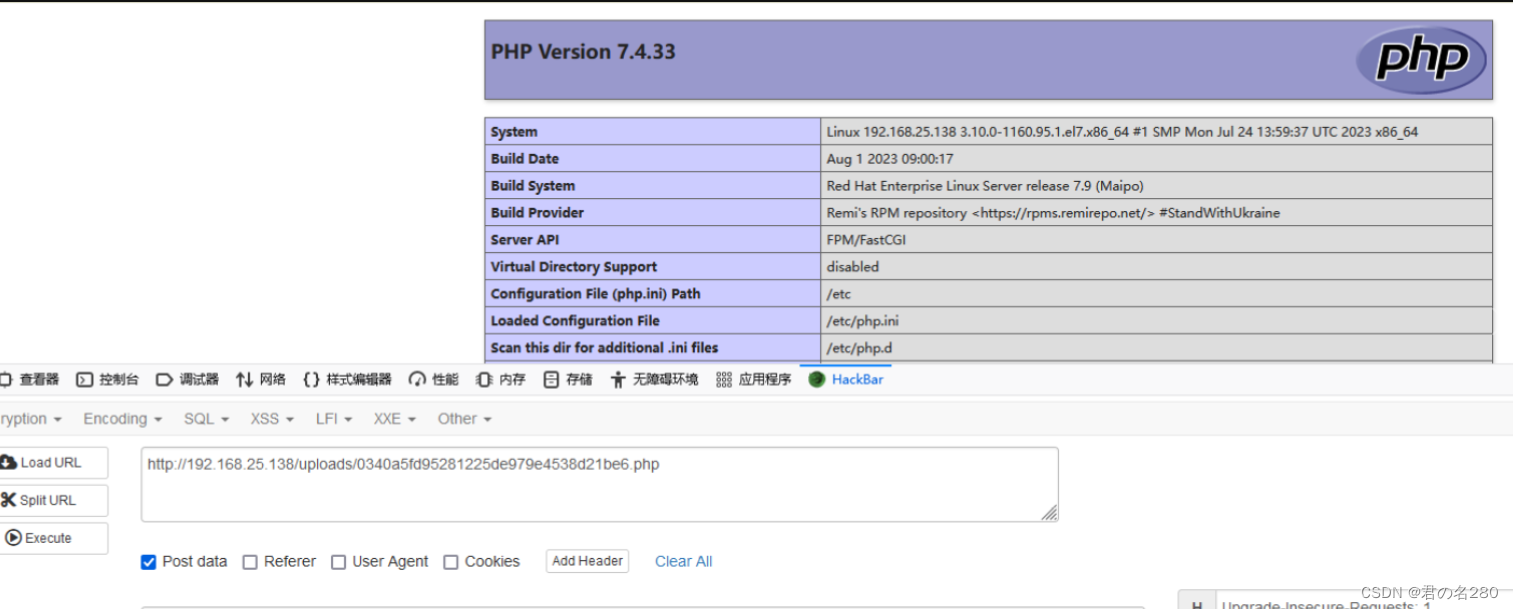
通过LD_PRELOAD绕过disable_functions
LD_PRELOAD LD_PRELOAD是Linux/Unix系统的一个环境变量,它可以影响程序的运行时的链接,它允许在程序运行前定义优先加载的动态链接库。通过这个环境变量,可以在主程序和其动态链接库的中间加载别的动态链接库,甚至覆盖系统的函数…...
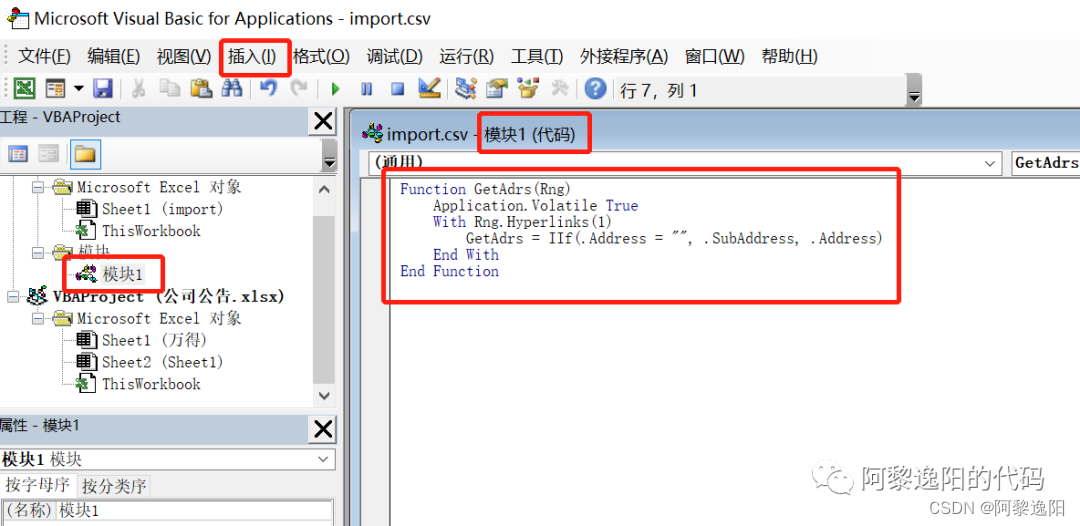
Python批量爬虫下载文件——把Excel中的超链接快速变成网址
本文的背景是:大学关系很好的老师问我能不能把Excel中1000个超链接网址对应的pdf文档下载下来。虽然可以手动一个一个点击下载,但是这样太费人力和时间了。我想起了之前的爬虫经验,给老师分析了一下可行性,就动手实践了。 没…...
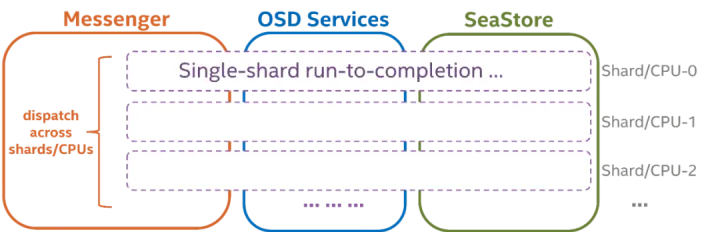
Crimson:高性能,高扩展的新一代 Ceph OSD
背景 随着物理硬件的不断发展,存储软件所使用的硬件的情况也一直在不断变化。 一方面,内存和 IO 技术一直在快速发展,硬件的性能在极速增加。在最初设计 Ceph 的时候,通常情况下,Ceph 都是被部署到机械硬盘上&#x…...

【websocket】websocket-client 与 websockets
websocket-client websocket-client 是 websocket 客户端,提供了对ws低级API的访问。通过导入 websocket 库使用,websocket 库是基于事件驱动的设计模式,通过定义回调函数来处理接收到的消息、错误和连接关闭等事件。 优势: 兼容…...

Qt快速学习(一)--对象,信号和槽
目录 1.Qt概述 1.1 什么是Qt 2.2 手动创建 2.3 pro文件 2.4 一个最简单的Qt应用程序 3 第一个Qt小程序 3.1 按钮的创建 3.2 对象模型(对象树) 3.3 Qt窗口坐标体系 4 信号和槽机制 4.1 系统自带的信号和槽 4.2 自定义信号和槽 4.3信号槽的拓展 4…...
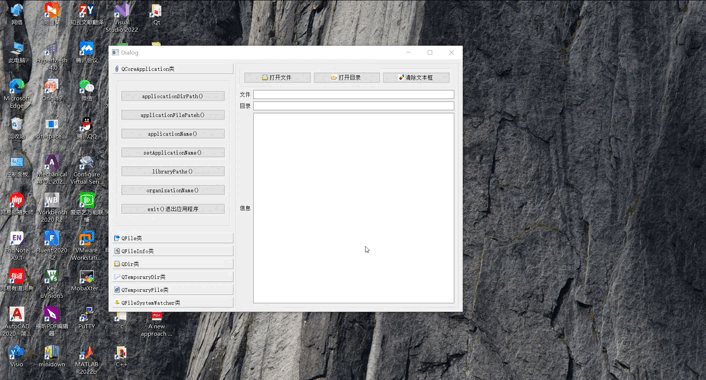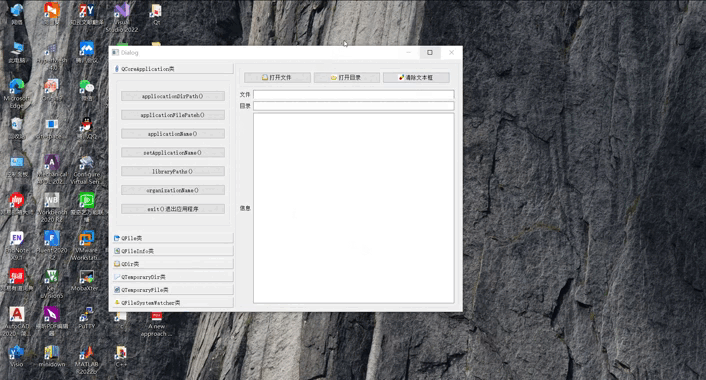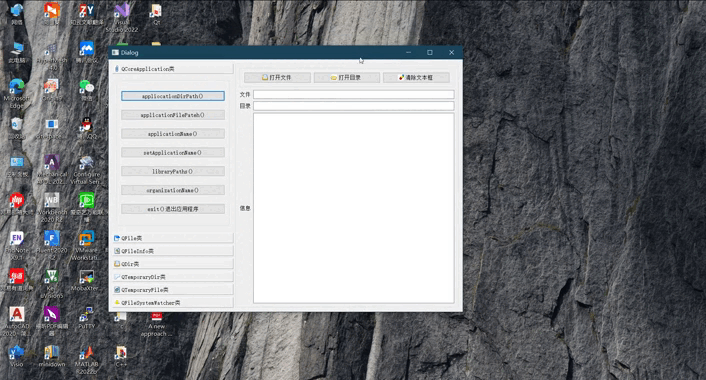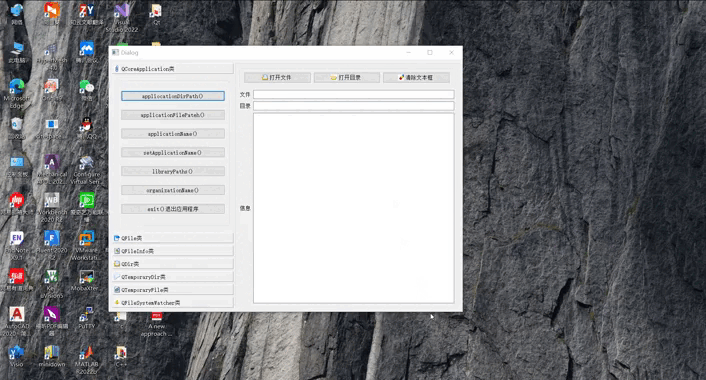
Qt6之如何为QDialog添加最大化和最小化按钮
在QDialog构造函数中添加以下几行代码: // 设置窗体最大化和最小化Qt::WindowFlags windowFlag Qt::Dialog;windowFlag | Qt::WindowMinimizeButtonHint;windowFlag | Qt::WindowMaximizeButtonHint;windowFlag …...

攻防世界-warmup
原题解题思路 只有一张图片,就查看源代码,有一个source.php。 查看source.php,白名单中还有一个hint.php。 hint.php告诉我们flag的位置ffffllllaaaagggg 但是直接跳转是没用的,构造payload。 http://61.147.171.105:55725/sourc…...

02__models
LangChain提供两种封装的模型接口 1.大规模语言模型(LLM):输入文本字符串,返回文本字符串 2.聊天模型:基于一个语言模型,输入聊天消息列表,返回聊天消息 Langchain的支持OpenAI、ChatGLM、Hu…...
MyBatis入门配置及CURD实现
目录 一、MyBatis简介 1. 什么是 MyBatis ? 2. MyBatis的特性 3. 什么是持久层框架? 二、MyBatis环境配置 2.1 创建maven工程 2.2 导入相关pom依赖 2.3 导入jdbc配置文件 2.4 Mybatis相关插件安装 3.5 Mybatis-cfg.xml 核心配置 2.6 引入Log4j2日志文件…...
《游戏编程模式》学习笔记(五)原型模式 Prototype Pattern
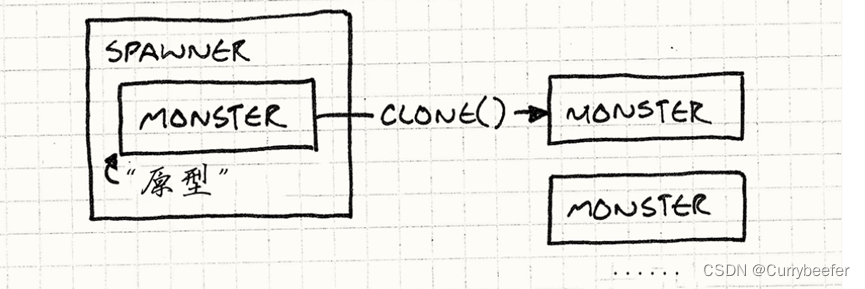
原型的定义 用原型实例指定创建对象的种类,并且通过拷贝这些原型创建新的对象。 举个例子 假设我现在要做一款游戏,这个游戏里有许多不同种类的怪物,鬼魂,恶魔和巫师。这些怪物通过“生产者”进入这片区域,每种敌人…...

ansible案列之LNMP分布式剧本
LNMP分布式剧本 一:环境设置二:编写Nginx剧本准备nginx下载源准备配置文件并开放PHP的访问路径准备php测试页面编写nginx剧本 三:编写Mysql剧本编写密码获取脚本准备Mysql的yum源编写mysql剧本 四:准备PHP剧本准备两个配置文件编写…...
React2023电商项目实战 - 1.项目搭建
古人学问无遗力,少壮工夫老始成。 纸上得来终觉浅,绝知此事要躬行。 —— 陆游《《冬夜读书示子聿》》 系列文章目录 项目搭建App登录及网关App文章自媒体平台(博主后台)内容审核(自动) 文章目录 系列文章目录一、项目介绍1.页面…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

