【LeetCode动态规划】详解买卖票I~IV,经典dp题型买
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
思路
买卖股票除了确定买卖日期之外,还需要确定当天股票的状态
股票状态有两种:持有和不持有
为什么不用"买入"和"卖出"来作为状态?
因为买入和卖出仅能代表两种状态,即买入和卖出
什么意思呢?就比如第i天你卖出了股票,好那第i+1天如果你不买股票,那应该是什么状态?
如果还用“卖出”状态来表示,那么就意味着第i+1天仍然要卖出股票,但实际上我们想表示的是这样一种状态:“第i天卖出股票后,如果第i+1天不买,那么第i天卖掉股票后的状态应该持续到第i+1天”
因此,使用"买入"和"卖出"来作为状态会漏掉一些状态,还得单独为那些情况设定对应的状态进行表示
五步走
1、确定dp数组含义
根据思路,我们需要的dp数组应该是二维的
dp[i][0]:代表第i天持有股票所得到的最大收益
dp[i][1]:代表第i天不持有股票所得到的最大收益
这里在解释一下"持有"和"不持有"
持有指的是我现在手头上有某只股票,但不一定是今天买的,有可能是之前某一天买的,然后该状态延续到了现在
不持有指的是手头上已经没有股票了,但不一定是今天卖的,有可能是之前卖掉了,然后该状态持续到了现在(因为本题的股票只能买卖一次,因此该状态会持续到最后一天)
2、确定递推公式
因为dp的定义是"持有"和"不持有"两种,因此这两种情况需要分开讨论
(1)持有股票
第i天持有股票(dp[i][0])的状态可以通过两种情况推导得到:
- 第i天买了股票
- 第i - 1天之前买了股票
因为本题只能买卖一次股票,因此不管在哪天买入股票,都是第一次买入
因为我们的初始现金是0,所以在买入股票之后,此时的最大收益是 -price[i],即dp[i][0] = -price[i]。因为买股票花钱了嘛,此时的状态变为持有股票
然后如果是第i天不买入股票,但状态仍是持有股票的话,那么此时的状态是dp[i][0] = dp[i - 1][0]
综上,取两者最大的情况,那么持有股票时的递推公式为:dp[i][0] = max(dp[i - 1][0], -price[i])
(2)不持有股票
第i天持有股票(dp[i][1])的状态可以通过两种情况推导得到:
- 第i天卖了股票
- 第i - 1天之前卖了股票
如果是在第i天卖了股票,那么此时除了状态需要转换为持有股票(并且是i - 1天持有,因为第i天卖掉了就不持有了),还需要加上第i天的股价price[i]作为收益,即dp[i][1] = price[i] + dp[i - 1][0]
也就是说,如果当前的状态是不持有并且原因是,那在第i天还没卖股票时,此时的状态应该是
dp[i][0],卖掉之后状态转变为dp[i][1]显然不能用
dp[i][1] = dp[i][0]来表示这件事情那么可以用
price[i]表示第i天卖了股票(因为得到了收益),然后再用dp[i - 1][0]表示我前一天确实有这个股票两件事情加起来就可以证明我在第i天卖了股票
如果是在第i - 1天之前卖了股票,那么此时状态还是不持有股票,即dp[i][1] = dp[i - 1][1]
综上,取两者最大的情况,那么不持有股票时的递推公式为:dp[i][1] = max(dp[i - 1][1], price[i] + dp[i - 1][0])
3、初始化dp数组
从两种情况下的递推公式来看,dp[0][1]和dp[0][0]是递推的基础,因此需要对其进行初始化
结合dp数组的定义,dp[0][1]是第0天不持有股票所得到的最大收益,那没有股票肯定是0啊,而且我们初始资金也是0,即dp[0][1]=0
而dp[0][0]则是第0天持有股票所得到的最大收益,因为是第0天,所以不会存在前一天的情况
因此持有的股票一定是第0天购买的,所以dp[0][0] = -price[i]
4、确定遍历顺序
dp[i][1]由dp[0][1]推导而来,因此需要顺序遍历
代码
class Solution {
public:int maxProfit(vector<int>& prices) {int len = prices.size();if(len == 0) return 0;//定义dp数组vector<vector<int>> dp(len, vector<int>(2));//初始化dp[0][0] = -prices[0];dp[0][1] = 0;//遍历dp数组for(int i = 1; i < len ;++i){dp[i][0] = max(dp[i - 1][0], -prices[i]);//持有股票dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);//不持有股票}return dp[len - 1][1];}
};
为什么返回值是
dp[len - 1][1]而不是max(dp[len][0], dp[len][1])?
如果认为max(dp[len][0], dp[len][1])是返回值的话,存在两个错误
(1)len - 1才是最后一天,不是len
(2)题目要求最大利润,但没有要求具体在哪个状态达成
在这个题目中,只需要求最终的最大利润,而不需要知道具体是在哪个状态(持有股票或不持有股票)达到了最大利润,因此直接返回dp[len - 1][1]即可。这是因为题目中规定,最后一天必须卖出所有持有的股票,而不是可以选择继续持有。
在遍历到最后一天后,dp[len-1][0]表示最后一天持有股票的最大收益,而dp[len-1][1]则表示最后一天不持有股票的最大收益。
我们只需要考虑最后一天的状态,也就是持有股票和不持有股票的两种情况,因为最后一天无法再进行任何交易了,只有卖出股票才能获得收益。因此,我们只需要返回最后一天不持有股票的最大收益 dp[len-1][1] 即可。
买卖股票的最佳时机II
力扣题目链接(opens new window)
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
- 1 <= prices.length <= 3 * 10 ^ 4
- 0 <= prices[i] <= 10 ^ 4
思路
基本的思路和 I 一致
唯一不同的地方,就是推导dp[i][0]和dp[i][0]的时候,第i天买入股票的情况。
这里再推导一下所有的情况吧
(1)持有股票dp[i][0]
如果是第i天买入的,那么要用没有持有该股票时有的钱减去股票的售价,即dp[i][0] = dp[i - 1][1] - prices[i]
如果是第i-1天买入的,就还是和上一题一样,状态延续到第i天即可,即dp[i][0] = dp[i - 1][0]
综上,dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);//持有
(2)不持有股票dp[i][1]
如果是第i天卖掉的,那就要用持有该股票时有的钱加上卖股票得的钱,即dp[i][1] = dp[i - 1][0] + prices[i]
如果是第i-1天卖掉的,延续第i天的状态即可,即dp[i][1] = dp[i - 1][1]
综上,dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);//不持有
代码
class Solution {
public:int maxProfit(vector<int>& prices) {int len = prices.size();//获取prices数组长度(天数)if(len == 0 ) return 0;vector<vector<int>> dp(len, vector<int>(2));//创建dp数组dp[0][0] = -prices[0];//初始化dp[0][1] = 0;for(int i = 1; i < len; ++i){dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);//持有dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);//不持有}return dp[len - 1][1];//最后一天要求把股票卖掉,返回不持有股票的最大金钱数}
};
买卖股票的最佳时机III
力扣题目链接(opens new window)
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1: 输入:prices = [3,3,5,0,0,3,1,4] 输出:6 解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3。
示例 2: 输入:prices = [1,2,3,4,5] 输出:4 解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3: 输入:prices = [7,6,4,3,1] 输出:0 解释:在这个情况下, 没有交易完成, 所以最大利润为0。
示例 4: 输入:prices = [1] 输出:0
提示:
- 1 <= prices.length <= 10^5
- 0 <= prices[i] <= 10^5
思路
与之前的两题最大的不同是,之前一天只可以进行一次交易(买卖),总的交易次数也只有1次
而现在一天可以交易两次,总的次数也是两次
至多买卖两次,意味着可以买卖一次,可以买卖两次,也可以不买卖。
五步走
1、确定dp数组含义
回忆一下,之前只能买卖一次时,我们有两种情况,即:第i天持有或不持有股票
现在因为可以进行两次买卖,所以第i天可能有的所有情况(假设在第i天就进行两次交易,就会有四种情况)有四种:
- 0、没有操作--
dp[i][0] - 1、第i天第一次持有股票--
dp[i][1] - 2、第i天第一次不持有股票--
dp[i][2] - 3、第i天第二次持有股票--
dp[i][3] - 4、第i天第二次不持有股票--
dp[i][4]
即dp[i][j]中,i表示第i天,j表示状态
dp[i][j]表示第i天状态j所剩最大现金
2、确定递推公式
dp[i][0]先不用管,后面要初始化
达到dp[i][1]状态(第一次持有股票),有两个具体操作:
- 操作一:第i天买入股票了,那么
dp[i][1] = dp[i-1][0] - prices[i](用前一天状态下还剩的钱减去第i天买入股票的价格) - 操作二:第i天没有操作,而是沿用前一天买入的状态,即:
dp[i][1] = dp[i - 1][1]
取最大结果:dp[i][1] = max(dp[i- 1][0] - prices[i], dp[i - 1][1]);
dp[i][2](第一次不持有股票)同理:
- 操作一:第i天卖出股票了,那么
dp[i][2] = dp[i - 1][1] + prices[i]( ) - 操作二:第i天没有操作,沿用前一天卖出股票的状态,即:
dp[i][2] = dp[i - 1][2]
取最大结果:dp[i][2] = max(dp[i - 2][1] - prices[i], dp[i - 1][2]);
按上面的形式可以把剩余的情况在不同操作下的状态推导出来:
dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
3、初始化dp数组
(1)如果第0天没有操作,那就是0,即dp[0][0] = 0
(2)如果第0天第一次操作
- 在第0天第一次买入,初始现金为0,那么现在要扣除买股票的钱,即
dp[0][1] = -prices[0] - 在第0天第一次卖出,即
dp[0][2] = 0
如果第0天的第一次操作就是卖出,那此时都没有东西,卖什么呢?
这种情况可以理解为在同一天先买入了,然后又在当天卖出
买卖都是相同的价格,相当于钱花出去了又原路返回,因此
dp[0][2] = 0由此我们可以发现,第一次卖出的操作是依赖第一次买入操作的
(3)如果第0天第二次操作
- 在第0天第二次买入。
dp[0][3] = -prices[0]
所谓的“第二次买入”,意味着我之前已经买入过一次了,也就是说第二次买入依赖于第一次卖出的状态
又因为题目规定买完必须先卖掉才能再买,所以“第二次买入”时,已经经过了第一次买入和卖出
因此在第0天第二次买入时,手头上的钱仍然是0,那么买入之后的状态自然就是 -prices[0]
- 在第0天第二次卖出。
dp[0][4] = 0
与在第0天第一次卖出同理
4、确定遍历顺序
i由i-1推出,因此仍是从小到大遍历,即顺序遍历
代码
class Solution {
public:int maxProfit(vector<int>& prices) {if (prices.size() == 0) return 0;//创建dp数组vector<vector<int>> dp(prices.size(), vector<int>(5, 0));//初始化,根据分析进行初始化dp[0][1] = -prices[0];dp[0][3] = -prices[0];//遍历dp数组for(int i = 1; i < prices.size(); ++i){dp[i][0] = dp[i - 1][0];//不进行操作//第i天第一次进行操作dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);//不操作|买入股票,用前一天状态下还剩的钱减去第i天买入股票的价格dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);//不操作|卖出股票,用前一天状态下还剩的钱加上第i天卖掉股票的收益//第i天第二次进行操作dp[i][3] = max(dp[i - 1][3],dp[i - 1][2] - prices[i]);//不操作|买入股票dp[i][4] = max(dp[i - 1][4],dp[i - 1][3] + prices[i]);//不操作|卖出股票}return dp[prices.size() - 1][4];}
};
买卖股票的最佳时机IV
力扣题目链接(opens new window)
给定一个整数数组 prices ,它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1: 输入:k = 2, prices = [2,4,1] 输出:2 解释:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2。
示例 2: 输入:k = 2, prices = [3,2,6,5,0,3] 输出:7 解释:在第 2 天 (股票价格 = 2) 的时候买入,在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4。随后,在第 5 天 (股票价格 = 0) 的时候买入,在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。
提示:
- 0 <= k <= 100
- 0 <= prices.length <= 1000
- 0 <= prices[i] <= 1000
思路
本题与上题的不同点在于买卖次数,现在我们可以任意买卖k次了
从上题来看,买卖两次已经需要列出4个状态了(不算不操作状态),因此在k次交易的条件下,罗列处所有状态是可能的
需要使用循环去控制
五步走
1、dp数组的含义
与上一题一样
二维数组 dp[i][j] :dp[i][j]表示第i天状态j所剩最大现金
j的状态可以表示为:
- 0 表示不操作
- 1 第一次买入
- 2 第一次卖出
- 3 第二次买入
- 4 第二次卖出
- .....
除了0以外,上述状态的规律可以总结为:偶数卖出,奇数买入
因为买卖次数变成k次,每多一次买卖会新增两种状态,所以dp数组的大小要设置为2k + 1
vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));
2、确定递推公式
正如上面的分析,k次买卖的话是不可能都列出来所有状态的,因此需要进行抽象,抽象出一个通用的递推公式
先来看看上一题中,两次买卖时的递推公式:
dp[i][0] = dp[i - 1][0];//不进行操作//第i天第一次进行操作dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);//不操作|买入股票,用前一天状态下还剩的钱减去第i天买入股票的价格dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);//不操作|卖出股票,用前一天状态下还剩的钱加上第i天卖掉股票的收益//第i天第二次进行操作dp[i][3] = max(dp[i - 1][3],dp[i - 1][2] - prices[i]);//不操作|买入股票dp[i][4] = max(dp[i - 1][4],dp[i - 1][3] + prices[i]);//不操作|卖出股票
这里可以发现,二维dp数组中,第二个维度我们是写成具体数字的,用来表示买入和卖出状态
可以使用一个变量j来代替具体的数字,j + 1表示买入;j + 2表示卖出
使用for循环控制j,j从0开始循环,每次自增2
for(int j = 0; i < 2 * k; j += 2){dp[i][j] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);//不操作|奇数买入,用前一天状态下还剩的钱减去第i天买入股票的价格dp[i][j] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);//不操作|偶数卖出,用前一天状态下还剩的钱加上第i天卖掉股票的收益
}
类比j为奇数是买,偶数是卖的状态。
为什么j是小于2 * k,而不是别的值,比如2 * k - 1 ?
遇到边界不确定的情况时,就代入具体值来判断是否合理
这里假设一共至多可以买卖2次
如果j < 2 * k ,那么 j < 4
以上面 两次买卖时的递推公式 为例来看
当循环开始,
j = 0,所以 j + 1 指向
dp[i][1], j + 2 指向dp[i][2],一切正常j = 2,所以 j + 1 指向
dp[i][3], j + 2 指向dp[i][4],一切正常j = 3,所以 j + 1 指向
dp[i][3], j + 2 指向dp[i][4],一切正常j = 4,循环结束,所有状态被完整覆盖,边界正确
3、初始化dp数组
基本上与买卖III的思路一致
(1)如果第0天没有操作,那就是0,即dp[0][0] = 0
(2)如果第0天第一次操作
- 在第0天第一次买入,初始现金为0,那么现在要扣除买股票的钱,即
dp[0][1] = -prices[0] - 在第0天第一次卖出,即
dp[0][2] = 0
(3)如果第0天第二次操作
- 在第0天第二次买入。
dp[0][3] = -prices[0] - 在第0天第二次卖出。
dp[0][4] = 0
(关于推导的细节与注释详见买卖III)
我们还是从上面初始化中总结规律进行抽象
即:j为奇数时候,要初始化为-prices[0];j为偶数时候,要初始化为0;
使用for循环进行初始化
for(int j = 1; j < 2 * k; j += 2){dp[0][j] = -prices[0];//0在创建dp数组的时候就初始化了
}
为什么j是小于2 * k,而不是别的值,比如2 * k - 1 ?
还是代入来看, 这里假设至多可以买卖2次,那么 j < 4
当j = 1时,奇数初始化为-prices[0]
然后自增2,j = 3,奇数初始化为-prices[0]
再自增就超过4,结束循环,过程没有问题
4、确定遍历顺序
i由i-1推出,因此仍是从小到大遍历,即顺序遍历
代码
class Solution {
public:int maxProfit(int k, vector<int>& prices) {if(prices.size() == 0) return 0;//创建dp数组vector<vector<int>> dp(prices.size() + 1, vector<int>(2 * k + 1, 0));//初始化dp数组for(int j = 1; j < 2 * k; j += 2){dp[0][j] = -prices[0];//0在创建dp数组的时候就初始化了,所以不用在此处初始化}//遍历dp数组for(int i = 1; i < prices.size(); ++i){for(int j = 0; j < 2 * k; j += 2){//不操作|奇数买入,用前一天状态下还剩的钱减去第i天买入股票的价格dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);//不操作|偶数卖出,用前一天状态下还剩的钱加上第i天卖掉股票的收益dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);}}return dp[prices.size() - 1][2 * k];//返回最后一天卖掉股票后的总金额}
};相关文章:

【LeetCode动态规划】详解买卖票I~IV,经典dp题型买
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。 返回你可以从这笔交易中获取的最大利润。…...

【深入探究人工智能】:常见机器学习算法总结
文章目录 1、前言1.1 机器学习算法的两步骤1.2 机器学习算法分类 2、逻辑回归算法2.1 逻辑函数2.2 逻辑回归可以用于多类分类2.3 逻辑回归中的系数 3、线性回归算法3.1 线性回归的假设3.2 确定线性回归模型的拟合优度3.3线性回归中的异常值处理 4、支持向量机(SVM&a…...

设计模式之解释器模式详解及实例
1、解释器设计模式概述: 解释器模式(Interpreter Pattern)是一种设计模式,它主要用于描述如何构建一个解释器以解释特定的语言或表达式。该模式定义了一个文法表示和解释器的类结构,用于解释符合该文法规则的语句。解…...
Nodejs沙箱逃逸--总结
一、沙箱逃逸概念 JavaScript和Nodejs之间有什么区别:JavaScript用在浏览器前端,后来将Chrome中的v8引擎单独拿出来为JavaScript单独开发了一个运行环境,因此JavaScript也可以作为一门后端语言,写在后端(服务端&#…...

No115.精选前端面试题,享受每天的挑战和学习
文章目录 变量提升和函数提升的顺序Event Loop封装 FetchAPI,要求超时报错的同时,取消执行的 promise(即不继续执行)强缓存和协商缓存的区别token可以放在cookie里吗? 变量提升和函数提升的顺序 在JavaScript中&#…...
Elasticsearch:语义搜索 - Semantic Search in python
当 OpenAI 于 2022 年 11 月发布 ChatGPT 时,引发了人们对人工智能和机器学习的新一波兴趣。 尽管必要的技术创新已经出现了近十年,而且基本原理的历史甚至更早,但这种巨大的转变引发了各种发展的“寒武纪大爆炸”,特别是在大型语…...
Flink学习笔记(一)
流处理 批处理应用于有界数据流的处理,流处理则应用于无界数据流的处理。 有界数据流:输入数据有明确的开始和结束。 无界数据流:输入数据没有明确的开始和结束,或者说数据是无限的,数据通常会随着时间变化而更新。 在…...
[Raspberry Pi]如何用VNC遠端控制樹莓派(Ubuntu desktop 23.04)?
之前曾利用VMware探索CentOS,熟悉Linux操作系統的指令和配置運作方式,後來在樹莓派價格飛漲的時期,遇到貴人贈送Raspberry Pi 4 model B / 8GB,這下工具到位了,索性跳過樹莓派官方系統(Raspberry Pi OS),直…...

17.HPA和rancher
文章目录 HPA部署 metrics-server部署HPA Rancher部署Rancherrancher添加集群仪表盘创建 namespace仪表盘创建 Deployments仪表盘创建 service 总结 HPA HPA(Horizontal Pod Autoscaling)Pod 水平自动伸缩,Kubernetes 有一个 HPA 的资源&…...
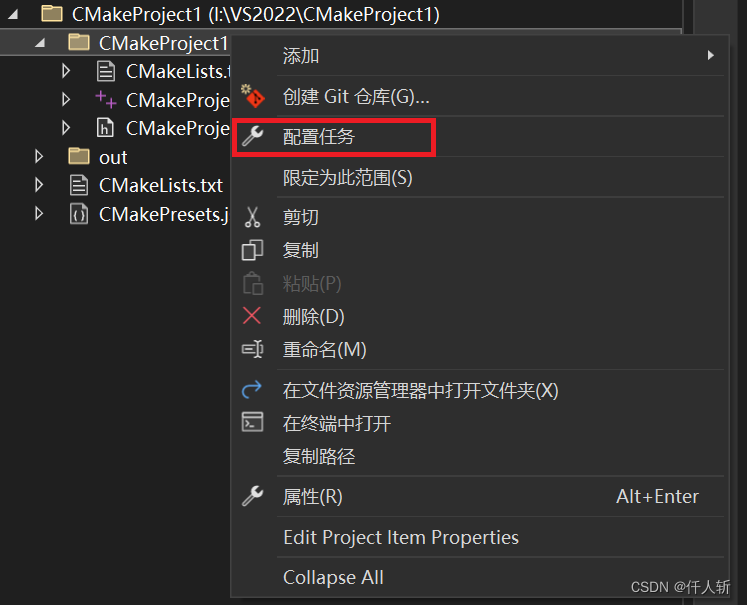
VS2022远程Linux使用cmake开发c++工程配置方法
文章目录 远程连接CMakePresets.json的配置Task.vs.json配置launch.vs.json配置最近使用别人在VS2015上使用visualgdb搭建的linux开发环境,各种不顺手,一会代码不能调转了,一会行号没了,调试的时候断不到正确的位置,取消的断点仍然会进。因此重新摸索了一套使用vs的远程开…...

《强化学习:原理与Python实战》——可曾听闻RLHF
前言: RLHF(Reinforcement Learning with Human Feedback,人类反馈强化学习)是一种基于强化学习的算法,通过结合人类专家的知识和经验来优化智能体的学习效果。它不仅考虑智能体的行为奖励,还融合了人类专家…...
STM32——RTC实时时钟
文章目录 Unix时间戳UTC/GMT 时间戳转换BKP简介BKP基本结构读写BKP备份寄存器电路设计关键代码 RTC简介RTC框图RTC基本结构硬件电路RTC操作注意事项读写实时时钟电路设计关键代码 Unix时间戳 Unix 时间戳(Unix Timestamp)定义为从UTC/GMT的1970年1月1日…...

webSocket 开发
1 认识webSocket WebSocket_ohana!的博客-CSDN博客 一,什么是websocket WebSocket是HTML5下一种新的协议(websocket协议本质上是一个基于tcp的协议)它实现了浏览器与服务器全双工通信,能更好的节省服务器资源和带宽…...
c#设计模式-结构型模式 之 代理模式
前言 由于某些原因需要给某对象提供一个代理以控制对该对象的访问。这时,访问对象不适合或者不能直接 引用目标对象,代理对象作为访问对象和目标对象之间的中介。在学习代理模式的时候,可以去了解一下Aop切面编程AOP切面编程_aop编程…...

openpnp - 自动换刀的设置
文章目录 openpnp - 自动换刀的设置概述笔记采用的openpnp版本自动换刀库的类型选择自动换刀设置前的注意事项先卸掉吸嘴座上所有的吸嘴删掉所有的吸嘴设置自动换刀的视觉识别设置吸嘴座为自动换刀 - 以N1为例备注补充 - 吸嘴轴差个0.3mm, 就有可能怼坏吸嘴END openpnp - 自动换…...
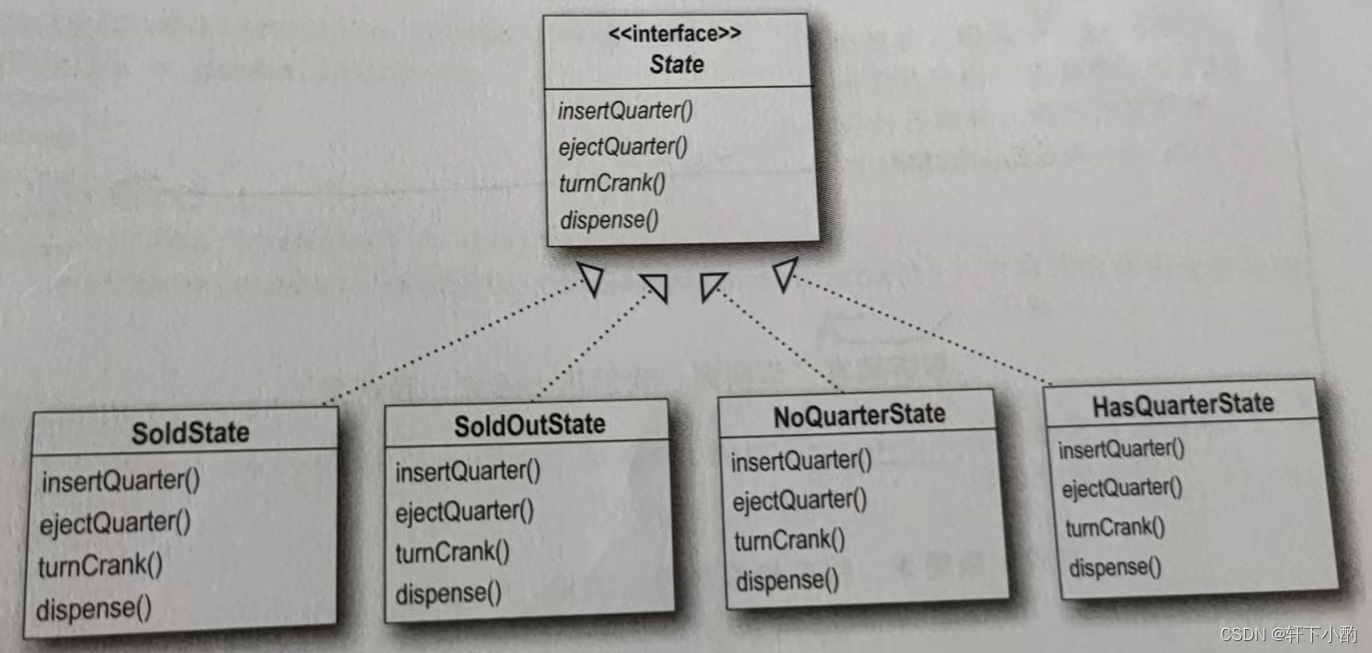
《HeadFirst设计模式(第二版)》第十章代码——状态模式
如下图所示,这是一个糖果机的状态机图,要求使用代码实现: 初始版本: package Chapter10_StatePattern.Origin;/*** Author 竹心* Date 2023/8/19**/public class GumballMachine {final static int SOLD_OUT 0;final static int…...
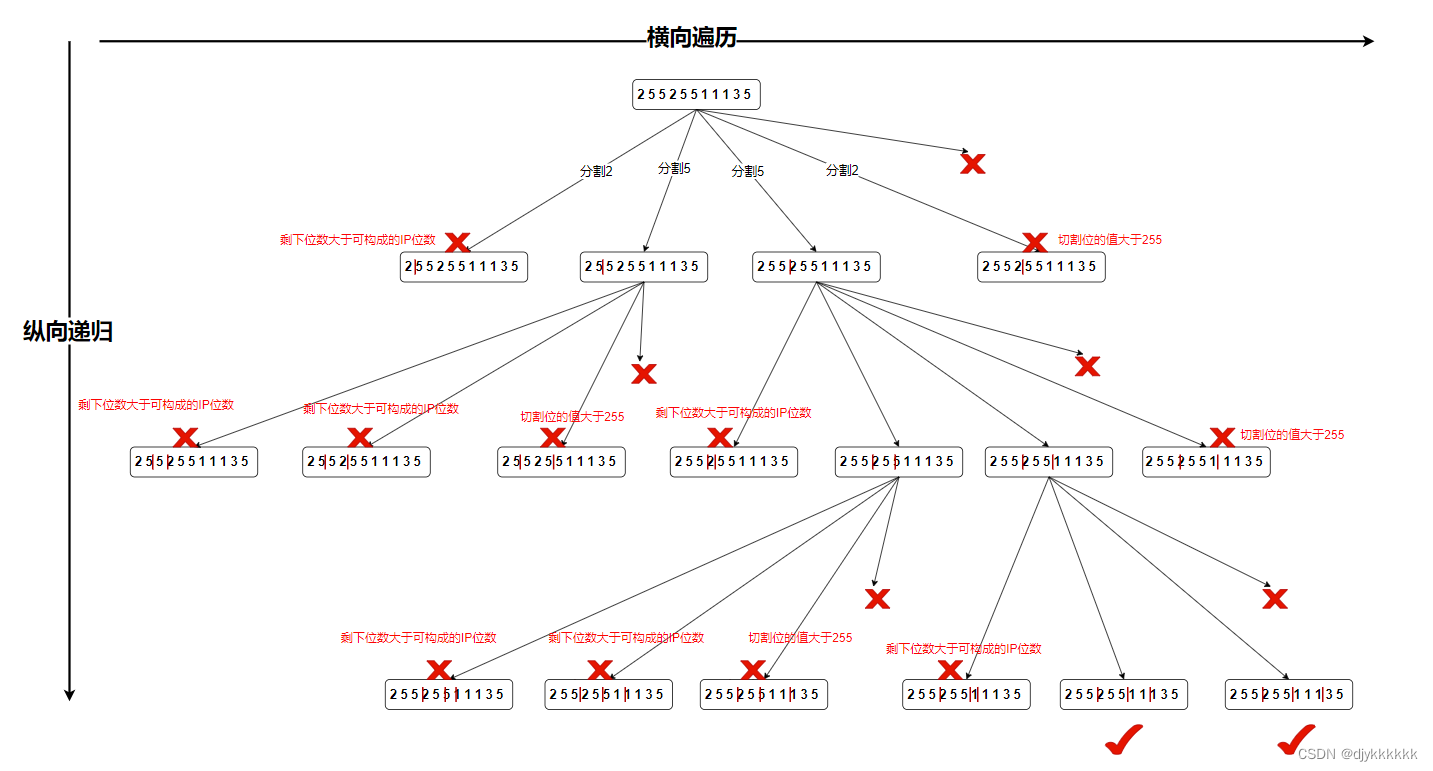
day-25 代码随想录算法训练营(19)回溯part02
216.组合总和||| 思路:和上题一样,差别在于多了总和,但是数字局限在1-9 17.电话号码的字母组合 思路:先纵向遍历第i位电话号码对于的字符串,再横向递归遍历下一位电话号码 93.复原IP地址 画图分析: 思…...

PG逻辑备份与恢复
文章目录 创建测试数据pg_dump 备份pg_restore 恢复pg_restore 恢复并行备份的文件PG 只导出指定函数 创建测试数据 drop database if exists test; create database test ; \c test create table t1(id int primary key); create table t2(id serial primary key, name varch…...
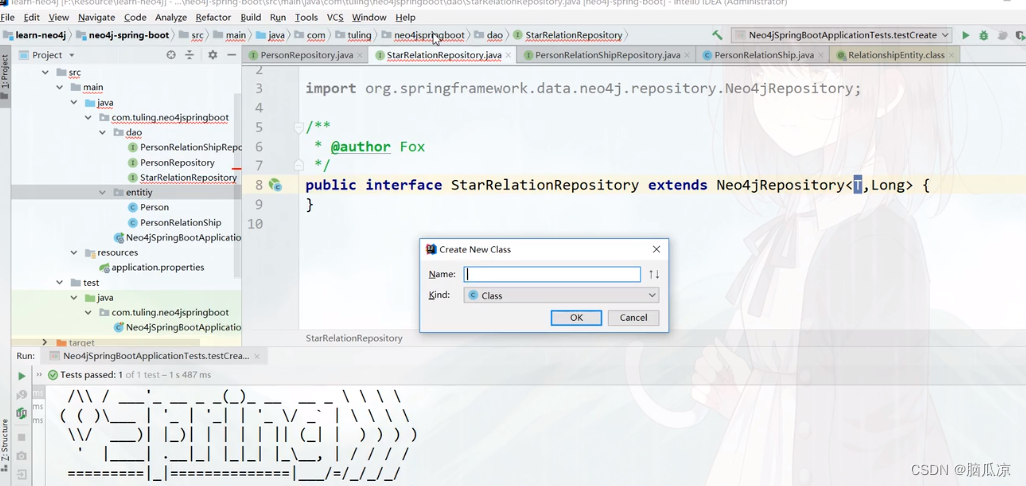
图数据库_Neo4j和SpringBoot整合使用_实战创建明星关系图谱---Neo4j图数据库工作笔记0010
然后我们再来看一下这个明星关系图谱 可以看到这里 这个是原来的startRelation 我们可以写CQL去查询对应的关系 可以看到,首先查询出来以后,然后就可以去创建 我们可以把写的创建明星关系的CQL,拿到 springboot中去执行 可以看到,这里我们先写一个StarRelationRepository,然…...
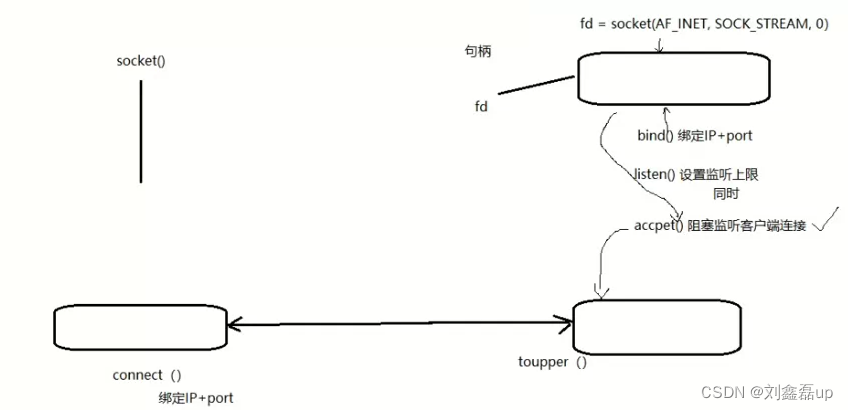
Linux网络编程:Socket套接字编程(Server服务器 Client客户端)
文章目录: 一:定义和流程分析 1.定义 2.流程分析 3.网络字节序 二:相关函数 IP地址转换函数inet_pton inet_ntop(本地字节序 网络字节序) socket函数(创建一个套接字) bind函数(给socket绑定一个服务器地址结…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...
