数学建模-模型详解(1)
规划模型
线性规划模型:
当涉及到线性规划模型实例时,以下是一个简单的示例:
假设我们有两个变量 x 和 y,并且我们希望最大化目标函数 Z = 5x + 3y,同时满足以下约束条件:
- x >= 0
- y >= 0
- 2x + y <= 10
- x + 2y <= 8
这是一个典型的线性规划问题,我们可以使用线性规划算法来求解最优解。
非线性模型:
非线性规划(Nonlinear Programming,NLP)是一类优化问题,目标函数和约束条件都是非线性的。下面是一个非线性规划模型的示例:
假设有一个制造商要生产两种产品A和B,每种产品的利润分别为x和y。制造商有两个工厂,每个工厂的生产能力有限。产品A的生产需要消耗一定数量的原材料和劳动力,产品B也是如此。制造商希望最大化利润,同时满足工厂的生产能力和原材料、劳动力的限制。
假设x和y分别表示产品A和B的生产数量,c1和c2表示两个工厂的生产能力,m1和m2表示原材料的供应量,l1和l2表示劳动力的供应量。利润函数为:
Profit = 5x + 8y
约束条件如下:
1. 工厂1的生产能力限制:
x <= c1
2. 工厂2的生产能力限制:
y <= c2
3. 原材料供应限制:
2x + 3y <= m1
4x + 2y <= m2
4. 劳动力供应限制:
3x + 2y <= l1
x + 2y <= l2
目标是最大化利润Profit。
这个问题可以表示为一个非线性规划模型,可以使用优化算法(如梯度下降法、牛顿法等)求解最优解。
多目标规划模型:
在多目标规划模型中当涉及到多目标规划模型实例时,有许多不同的案例可以讨论。以下是一些常见的多目标规划模型实例:
-
多目标线性规划:在这种情况下,目标函数是线性的,并且存在多个目标函数。例如,可以考虑一个生产问题,其中目标是最大化收益和最小化生产成本。
-
多目标整数规划:在这种情况下,目标函数是线性的,并且决策变量是整数。例如,可以考虑一个资源分配问题,其中目标是最大化利润和最小化资源使用量。
-
多目标非线性规划:在这种情况下,目标函数是非线性的。例如,可以考虑一个投资组合问题,其中目标是最大化收益和最小化风险。
预测模型
灰色预测模型:
灰色预测模型(Grey Prediction Model)是一种基于灰色系统理论的预测模型。它是由中国科学家陈纳德在1982年提出的。
灰色系统理论是一种系统分析与控制的方法,它适用于研究那些数据不完备、信息不充分、系统结构不明确的问题。在灰色系统理论中,将数据序列分为两个部分:已知数据和未知数据。已知数据是指已经知道的数据序列,未知数据是指未来需要预测的数据序列。
灰色预测模型通过对已知数据的分析,建立数学模型,然后利用该模型对未知数据进行预测。常用的灰色预测模型有GM(1,1)模型和GM(2,1)模型。
GM(1,1)模型是最常用的灰色预测模型之一,它假设已知数据序列满足一阶线性微分方程,通过对该方程进行求解,可以得到未知数据的预测值。GM(2,1)模型是在GM(1,1)模型的基础上进行改进得到的,它考虑了数据的二阶累加特性,提高了预测的准确性。
灰色预测模型在很多领域都有广泛的应用,例如经济预测、环境预测、能源预测等。它具有简单、快速、准确的特点,适用于数据量较小、数据质量较差的情况下进行预测。然而,灰色预测模型也有一些限制,例如对数据的要求较高、不适用于非线性系统等。
总之,灰色预测模型是一种基于灰色系统理论的预测模型,通过对已知数据的分析建模,对未知数据进行预测。它在某些情况下可以提供较为准确的预测结果,但也需要根据具体问题进行合理的应用。
最短路径问题:
最短路径模型是一种用于寻找图中最短路径的算法或模型。在图论中,最短路径是指两个顶点之间的最短距离或最小权重的路径。最短路径模型可以应用于许多领域,例如网络路由、物流规划、交通导航等。
常见的最短路径算法包括:
1. Dijkstra算法:Dijkstra算法用于解决带权重的单源最短路径问题,即从一个顶点出发,找到到达图中其他所有顶点的最短路径。
2. Bellman-Ford算法:Bellman-Ford算法用于解决带权重的单源最短路径问题,与Dijkstra算法不同的是,Bellman-Ford算法可以处理带有负权重的图。
3. Floyd-Warshall算法:Floyd-Warshall算法用于解决带权重的全源最短路径问题,即找到图中任意两个顶点之间的最短路径。
4. A*算法:A*算法是一种启发式搜索算法,常用于解决带权重的单源最短路径问题。它通过估计到目标顶点的距离来指导搜索过程,以提高搜索效率。
这些算法在不同的场景下有不同的适用性和性能特点,选择最合适的算法取决于具体的问题和需求。
相关文章:
)
数学建模-模型详解(1)
规划模型 线性规划模型: 当涉及到线性规划模型实例时,以下是一个简单的示例: 假设我们有两个变量 x 和 y,并且我们希望最大化目标函数 Z 5x 3y,同时满足以下约束条件: x > 0y > 02x y < 10…...

MySQL 数据库表的基本操作
一、数据库表概述 在数据库中,数据表是数据库中最重要、最基本的操作对象,是数据存储的基本单位。数据表被定义为列的集合,数据在表中是按照行和列的格式来存储的。每一行代表一条唯一的记录,每一列代表记录中的一个域。 二、数…...
企业微信电脑端开启chrome调试
首先: Mac端调试开启的快捷键:control shift command d Window端调试开启的快捷键: control shift alt d 这边以Mac为例,我们可以在电脑顶部看到调试的入口: 然后我们点击 『浏览器、webView相关』菜单,勾选上…...
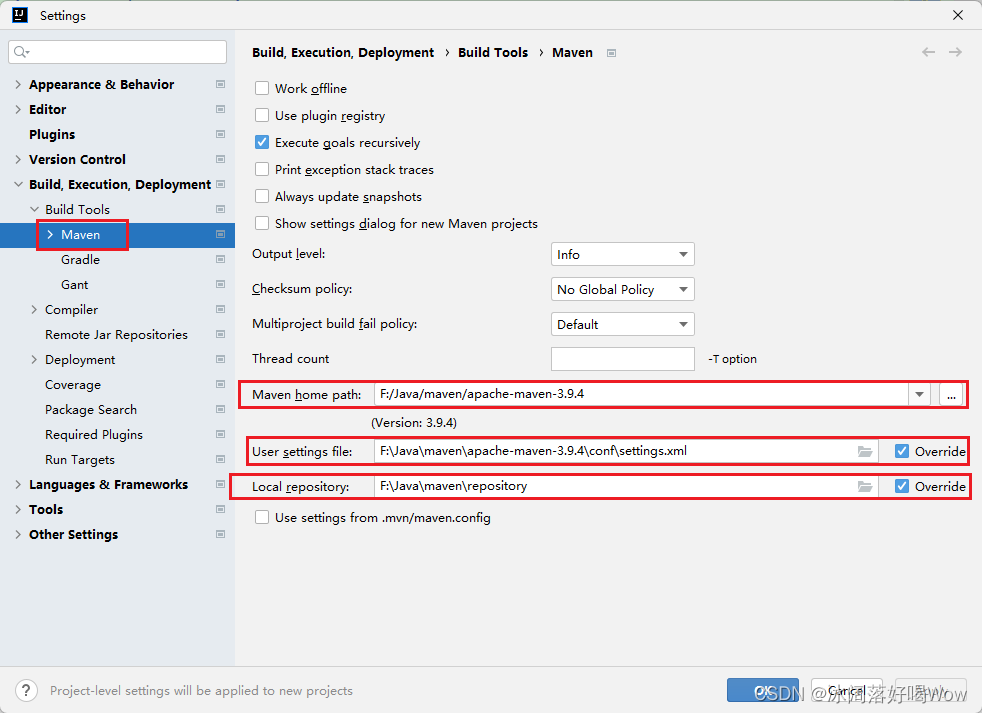
Maven官网下载配置新仓库
1.Maven的下载 Maven的官网地址:Maven – Download Apache Maven 点击Download,查找 Files下的版本并下载如下图: 2.Maven的配置 自己在D盘或者E盘创建一个文件夹,作为本地仓库,存放项目依赖。 将下载好的zip文件进行解…...

银河麒麟V10 达梦安装教程
安装前先准备要安装包,包需要需要区分X86和arm架构。 版本为:dm8_20230419_FTarm_kylin10_sp1_64.iso 达梦数据库下载地址: https://www.aliyundrive.com/s/Qm7Es5BQM5U 第一步创建用户 su - root 1. 创建安装用户组 dminstall。 groupad…...
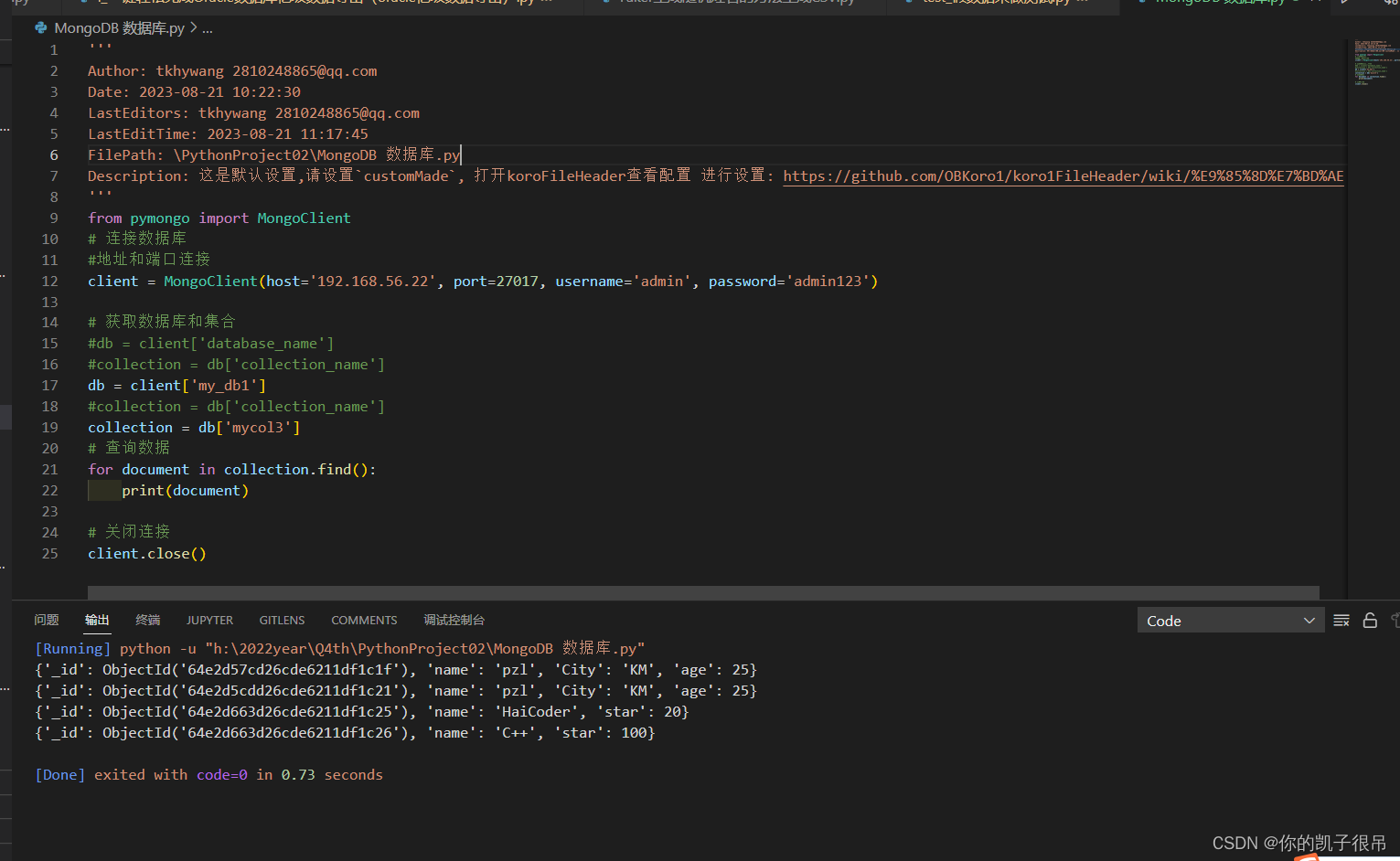
Python操作MongoDB数据库
安装MongoDB库 pip install pymongopython 代码 Author: tkhywang 2810248865qq.com Date: 2023-08-21 10:22:30 LastEditors: tkhywang 2810248865qq.com LastEditTime: 2023-08-21 11:17:45 FilePath: \PythonProject02\MongoDB 数据库.py Description: 这是默认设置,请设置…...
《HeadFirst设计模式(第二版)》第十一章代码——代理模式
代码文件目录: RMI: MyRemote package Chapter11_ProxyPattern.RMI;import java.rmi.Remote; import java.rmi.RemoteException;public interface MyRemote extends Remote {public String sayHello() throws RemoteException; }MyRemoteClient packa…...
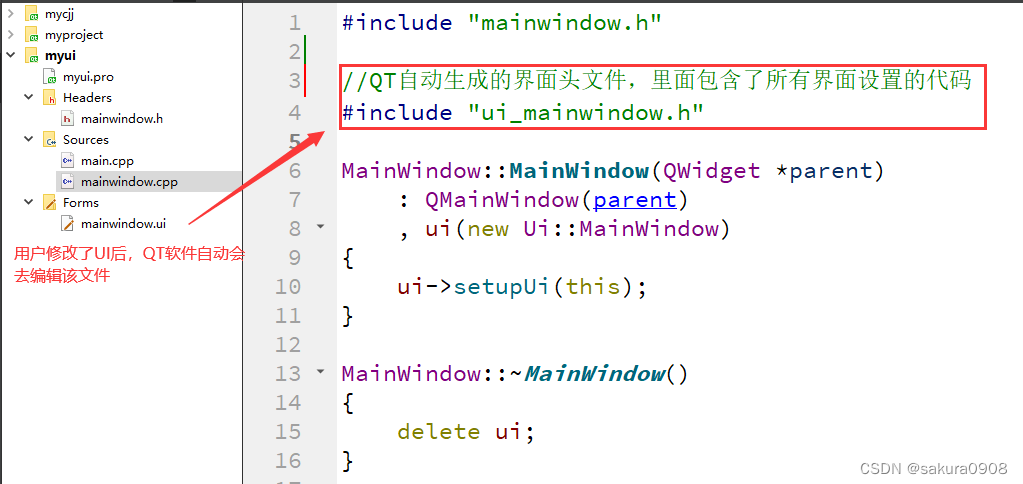
QT的工程文件认识
目录 1、QT介绍 2、QT的特点 3、QT模块 3.1基本模块 3.2扩展模块 4、QT工程创建 1.选择应用的窗体格式 2.设置工程的名称与路径 3.设置类名 4.选择编译器 5、QT 工程解析 xxx.pro 工程配置 xxx.h 头文件 main.cpp 主函数 xxx.cpp 文件 6、纯手工创建一个QT 工程…...
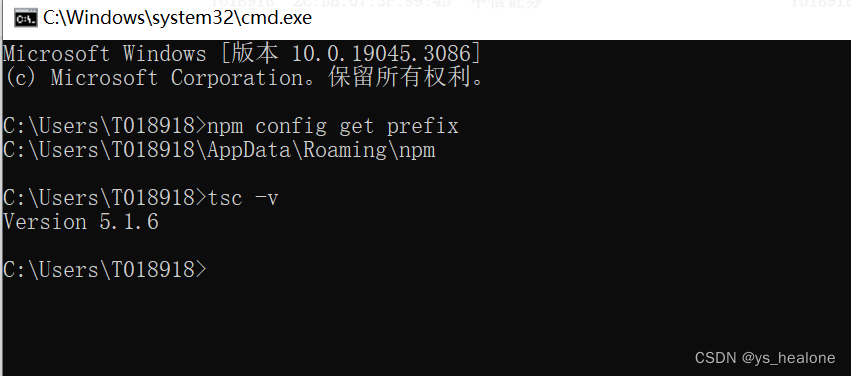
typeScript安装及TypeScript tsc 不是内部或外部命令,也不是可运行的程序或批处理文件解决办法
一、typeScript安装: 1、首先确定系统中已安装node, winr 输入cmd 打开命令行,得到版本号证明系统中已经安装node node -v //v18.17.0 2、使用npm 全局安装typeScript # 全局安装 TypeScript npm i -g typescript 二、检查是否安装成功ts #检查t…...

SWUST 派森练习题:P111. 摩斯密码翻译器
描述 摩斯密码(morse code),又称摩斯电码、摩尔斯电码(莫尔斯电码),是一种时通时断的信号代码,通过不同的信号排列顺序来表达不同的英文字母、数字和标点符号;通信时,将英文字母等内…...
如何在控制台查看excel内容
背景 最近发现打开电脑的excel很慢,而且使用到的场景很少,也因为mac自带了预览的功能。但是shigen就是闲不住,想自己搞一个excel预览软件,于是在一番技术选型之后,我决定使用python在控制台显示excel的内容。 具体的需…...
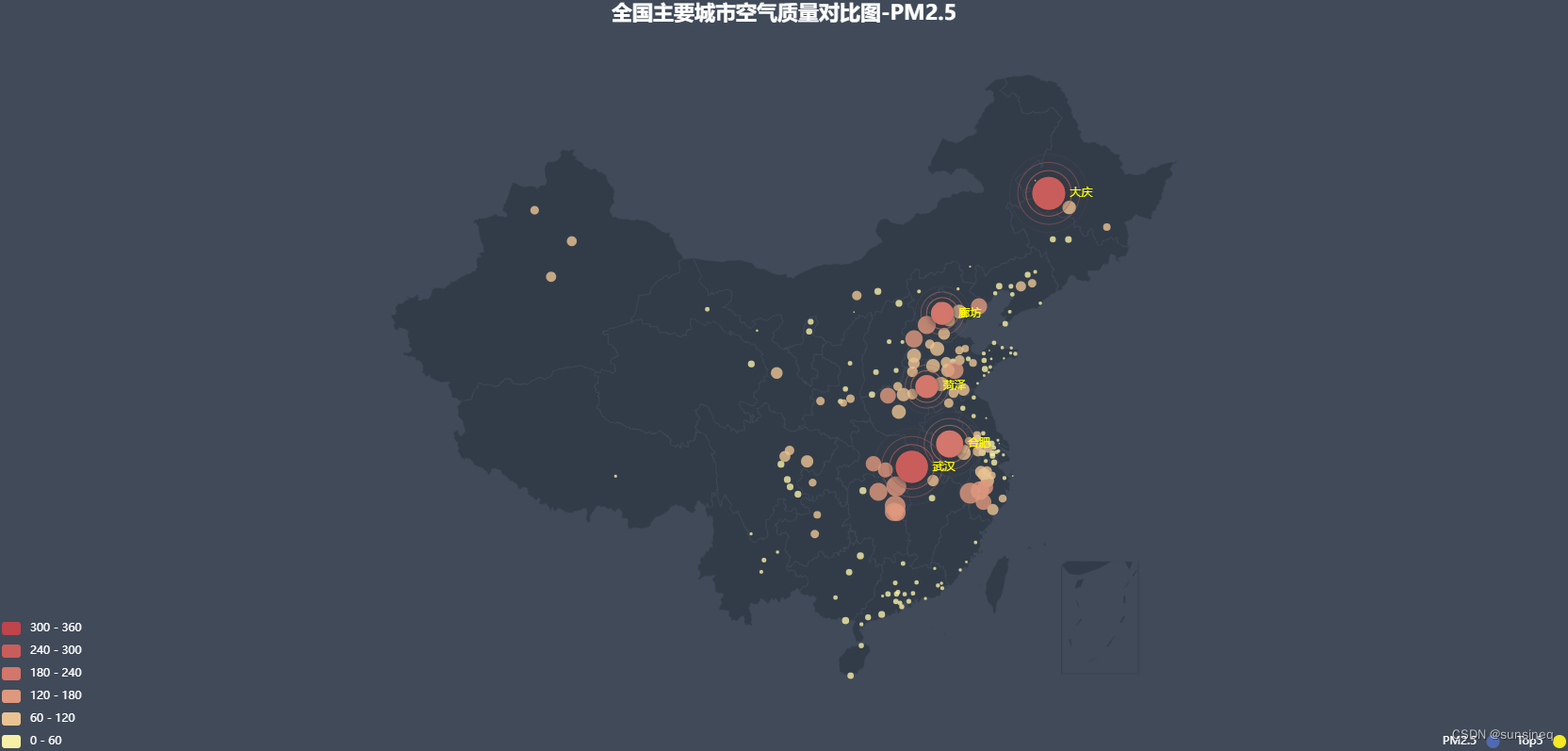
Echarts、js编写“中国主要城市空气质量对比”散点图 【亲测】
本次实验通过可视化工具Echarts来对全国主要城市的PM2.5的值进行直观的展示,使人们可以快速的发现信息的关键点,从而对各个城市的空气质量情况有直观的了解。 先看效果 上代码: <!DOCTYPE html> <html>&…...

linux不分区直接在文件系统根上开swap
root下,直接创swapfile dd if/dev/zero of/swapfile bs1M count8192然后 mkswap swapfile swapon swapfile修改fstab # /etc/fstab: static file system information. # # Use blkid to print the universally unique identifier for a # device; this may be us…...
React请求机制优化思路 | 京东云技术团队
说起数据加载的机制,有一个绕不开的话题就是前端性能,很多电商门户的首页其实都会做一些垂直的定制优化,比如让请求在页面最早加载,或者在前一个页面就进行预加载等等。随着react18的发布,请求机制这一块也是被不断谈起…...

CompletableFuture总结和实践
CompletableFuture被设计在Java中进行异步编程。异步编程意味着在主线程之外创建一个独立的线程,与主线程分隔开,并在上面运行一个非阻塞的任务,然后通知主线程进展,成功或者失败。 一、概述 1.CompletableFuture和Future的区别&…...
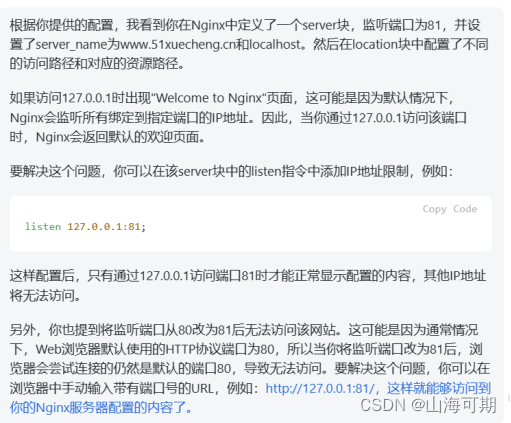
使用Nginx调用网关,然后网关调用其他微服务
问题前提:目前我的项目是已经搭建了网关根据访问路径路由到微服务,然后现在我使用了Nginx将静态资源都放在了Nginx中,然后我后端定义了一个接口访问一个html页面,但是html页面要用到静态资源,这个静态资源在我的后端是…...
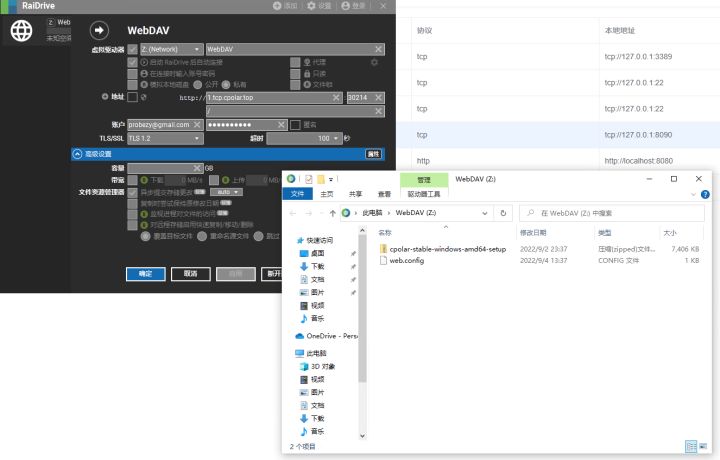
windows搭建WebDAV服务,并内网穿透公网访问【无公网IP】
windows搭建WebDAV服务,并内网穿透公网访问【无公网IP】 文章目录 windows搭建WebDAV服务,并内网穿透公网访问【无公网IP】1. 安装IIS必要WebDav组件2. 客户端测试3. cpolar内网穿透3.1 打开Web-UI管理界面3.2 创建隧道3.3 查看在线隧道列表3.4 浏览器访…...

PAT 1097 Deduplication on a Linked List
个人学习记录,代码难免不尽人意 Given a singly linked list L with integer keys, you are supposed to remove the nodes with duplicated absolute values of the keys. That is, for each value K, only the first node of which the value or absolute value o…...

Flink 数据集成服务在小红书的降本增效实践
摘要:本文整理自实时引擎研发工程师袁奎,在 Flink Forward Asia 2022 数据集成专场的分享。本篇内容主要分为四个部分: 小红书实时服务降本增效背景Flink 与在离线混部实践实践过程中遇到的问题及解决方案未来展望 点击查看原文视频 & 演…...
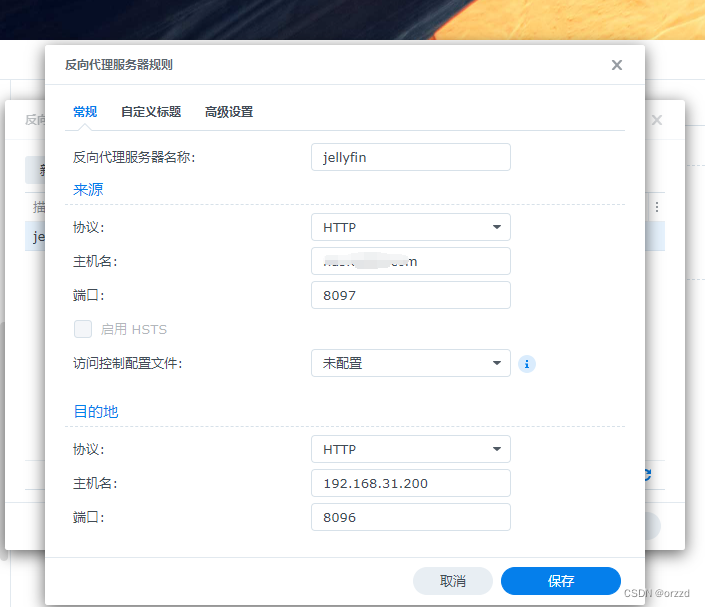
jellyfin使用ipv6+DDNS实现外网访问
前言 原本使用frp的方案进行外网访问jellyfin,但是阿里云的轻量服务器的带宽只有5M,只能支持看1080p的视频,看4K有点吃力,为了有更好的观影体验,选择ipv6DDNS的方式实现外网访问,此方案能跑满群晖的上行带宽…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...
