【C++习题集】-- 堆
(用于复习)
目录
树概念及结构
名词概念
二叉树概念及结构
特殊的二叉树
满二叉树
完全二叉树
运算性质
二叉树存储结构
顺序存储
链式存储
堆 - 顺序存储
堆的性质
堆的实现
堆的应用
堆排序
直接建堆法
树概念及结构
概念:非线性的数据结构(形成的倒挂似树的结构 - 根朝上,叶朝下,子树之间不能有交集)。

名词概念
- 节点的度:一个节点含有的子树的个数称为该节点的度。
- 叶节点或终端节点:度为0的节点称为叶节点。
- 非终端节点或分支节点:度不为0的节点。
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点。
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点。
- 兄弟节点:具有相同父节点的节点互称为兄弟节点。
- 树的度:一棵树中,最大的节点的度称为树的度。
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推。
- 树的高度或深度:树中节点的最大层次。
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟。
- 节点的祖先:从根到该节点所经分支上的所有节点。
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
- 森林:由m(m>0)棵互不相交的树的集合称为森林。
二叉树概念及结构
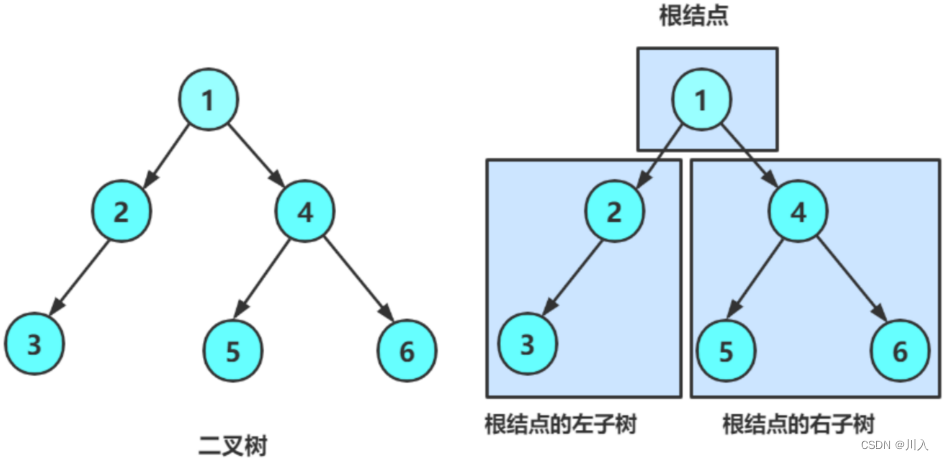
由一个根节点加上两棵别称为左子树和右子树的二叉树组成 - 子树可为空。

- 不存在度大于2的结点。
特殊的二叉树
满二叉树
每一个层的结点数都达到最大值,则结点总数:2^k - 1(K层数)。

完全二叉树
特殊的完全二叉树 - 最后一层不满,但是是左到右是连续的。
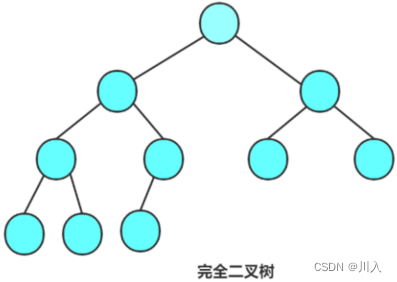
(满二叉树是特殊的完全二叉树)
运算性质
- 根节点的层数为1,则第i层上最多有2^(i - 1)个结点
- 根节点的层数为1,则深度h的最大结点数是2^h - 1
- 根节点的层数为1,n个结点的满二叉树的深度h = log2(n + 1)
- 如果度为0其叶结点个数为n,度为2的分支结点个数为m,则有:n = m + 1
- n个结点的完全二叉树,以数组顺序对所有节点开始编号:
- 若i>0,i位置节点的双亲序号:(i - 1) / 2
- 若2i + 1 < n,左孩子序号:2i + 1,2i + 1 >= n否则无左孩子
- 若2i + 2 < n,右孩子序号:2i + 2,2i + 2 >= n否则无右孩子
一个具有767个节点的完全二叉树,其叶子节点个数为()
A、383B、384C、385D、386------------------------------------------正确答案:B------------------------------------------解析:不要只想最后一层,倒数第二层也是会有叶子节点的。首先以:
可以推算出是第1 ~ 9层为满二叉树,对应节点数:511。可以知道最后一层一定为叶子节点:256个。
然后根据完全二叉树是最后一层不满,但是是左到右是连续的,于是256 / 2 = 128,所以倒数第二层有128个是最后一层的父节点。
再根据:
可知倒数第二层有256个节点,于是叶子节点:256 + 256 - 128 = 384。
二叉树存储结构
顺序存储
用数组来存储,适合表示完全二叉树。
- 物理上:数组
- 逻辑上:二叉树

链式存储
用链表来表示一棵二叉树。
- 二叉链:数据域和左右指针域
- 三叉链:数据域和左右上指针域

堆 - 顺序存储
堆是一种特殊的完全二叉树,只不过父亲与儿子节点间有关系。顺序存储的完全二叉树典型的就是堆。(普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储)
堆的性质
- 堆中某个节点的值总是不大于或不小于其父节点的值
- 小堆:父亲位,比孩子位,要小
- 大堆:父亲位,比孩子位,要大
- 堆总是一棵完全二叉树

堆的实现
#include <iostream>
#include <cassert>namespace qcr_heap
{typedef int HeapType;struct Heap{int64_t _capacity; // 动态开辟可用大小int64_t _size; // 实际数据占用大小HeapType *_array; // 动态开辟一维数组};/********** 初始化堆*********/void HeapInit(Heap *heap){assert(heap);heap->_capacity = 0;heap->_size = 0;heap->_array = 0;}/********** 销毁堆*********/void HeapDestory(Heap *heap){assert(heap);heap->_capacity = 0;heap->_size = 0;free(heap->_array);heap->_array = nullptr;}/********** 小根堆*********/bool less(HeapType element_1, HeapType element_2){return element_1 < element_2;}/********** 大根堆*********/bool greater(HeapType element_1, HeapType element_2){return element_1 > element_2;}/********** 交换数据*********/void swap(HeapType *element_1, HeapType *element_2){HeapType tmp = *element_1;*element_1 = *element_2;*element_2 = tmp;}/****************************** 向上调整* heap: 输入型参数,堆地址* child: 输入型参数,排序的插入节点* Func: 输入型参数,大小堆*****************************/void AdjustUp(Heap *heap, int64_t child, bool (*Func)(HeapType, HeapType)){assert(heap);int64_t parent = (child - 1) / 2;while (child > 0){if (Func(heap->_array[child], heap->_array[parent])){swap(&(heap->_array[child]), &(heap->_array[parent]));child = parent;parent = (child - 1) / 2;}elsebreak;}}/****************************** 向下调整* heap: 输入型参数,堆地址* root: 输入型参数,排序的根节点* Func: 输入型参数,大小堆*****************************/void AdjustDown(Heap *heap, int64_t root, bool (*Func)(HeapType, HeapType)){assert(heap);int64_t parent = root;int64_t child = parent * 2 + 1;while (child < heap->_size){if (child + 1 < heap->_size && Func(heap->_array[child + 1], heap->_array[child])){child++;}if (Func(heap->_array[child], heap->_array[parent])){swap(&(heap->_array[child]), &(heap->_array[parent]));parent = child;child = parent * 2 + 1;}else{break; // 符合堆就成立了,就没必要进行交换了。}}}/****************************** 存入数据* heap: 输入型参数,堆地址* data: 输入型参数,插入的数据* Func: 输入型参数,大小堆*****************************/void HeapPush(Heap *heap, HeapType data, bool (*Func)(HeapType, HeapType)){assert(heap);if (heap->_capacity == heap->_size){int64_t newcapacity = heap->_capacity == 0 ? 5 : heap->_capacity * 2;HeapType * tmp = (HeapType *)realloc(heap->_array, heap->_capacity*sizeof(HeapType);if (tmp == nullptr){printf("Capacuty Get Error!\n");exit(-1);}heap->_array = tmp;heap->_capacity = newcapacity;}heap->_array[heap->_size] = data;AdjustUp(heap, heap->_size, Func);(heap->_size)++;}/****************************** 按顺序全部输出* heap: 输入型参数,堆地址*****************************/void HeapPrint(Heap *heap){assert(heap);for (uint64_t i = 0; i < heap->_size; i++){std::cout << heap->_array[i] << " ";}std::cout << '\n';}/****************************** 首元素* heap: 输入型参数,堆地址*****************************/HeapType HeapTop(Heap *heap){assert(heap);assert(heap->_size > 0);return heap->_array[0];}/****************************** 判空* heap: 输入型参数,堆地址*****************************/bool HeapEmpty(Heap *heap){assert(heap);return heap->_size == 0;}/****************************** 有效数据个数* heap: 输入型参数,堆地址*****************************/int HeapSize(Heap *heap){assert(heap);return heap->_size;}/****************************** 判空* heap: 输入型参数,堆地址* Func: 输入型参数,大小堆*****************************/void HeapPop(Heap *heap, bool (*Func)(HeapType, HeapType)){assert(heap);assert(heap->_size > 0);heap->_array[0] = heap->_array[heap->_size - 1];(heap->_size)--;AdjustDown(heap, 0, Func);}
}已知小根堆为8,15,10,21,34,16,12,删除关键字 8 之后需重建堆,在此过程中,关键字之间的比较次数是()A、1B、2C、3D、4------------------------------------------正确答案:B------------------------------------------解析:首先我们需要知道,删除对应的调整算法是向下调整,所以其实在比较中有一个很重要的一项就是左右节点的比较,于是此处本质上的比较是需要在加上一次左右节点的比较。
堆的应用
堆排序
利用堆删除思想来进行排序。
TOP-K问题
1. 用数据集合中前K个元素来建堆
- 前k个最大的元素,则建小堆
- 前k个最小的元素,则建大堆
面试题 17.14. 最小K个数 - 力扣(LeetCode)
class Solution
{
public:// 向上建堆void adjustUp(vector<int> &nums, int child){int parent = (child - 1) / 2;while (child > 0){if (nums[child] > nums[parent]){swap(nums[child], nums[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}}// 向下建堆void adjustDown(vector<int> &nums, int parent){int child = parent * 2 + 1;while (child < nums.size()){if (child + 1 < nums.size() && nums[child + 1] > nums[child]){child++;}if (nums[child] > nums[parent]){swap(nums[child], nums[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}// 堆排序的TOP-k问题vector<int> smallestK(vector<int> &arr, int k){vector<int> nums;nums.reserve(k);// 前K个元素来建堆for (int i = 0; i < k; i++){nums.push_back(arr[i]);adjustUp(nums, nums.size() - 1);}// 对比堆顶元素if (k != 0){for (int i = k; i < arr.size(); i++){if (arr[i] < nums[0]){nums[0] = arr[i];adjustDown(nums, 0);}}}return nums;}
};并不是最优的,并且还实现了两个堆算法,编码效率过低。
直接建堆法
原本利用向上建堆的方式,是并不够完美的,建堆的时间复杂度为O(N)。
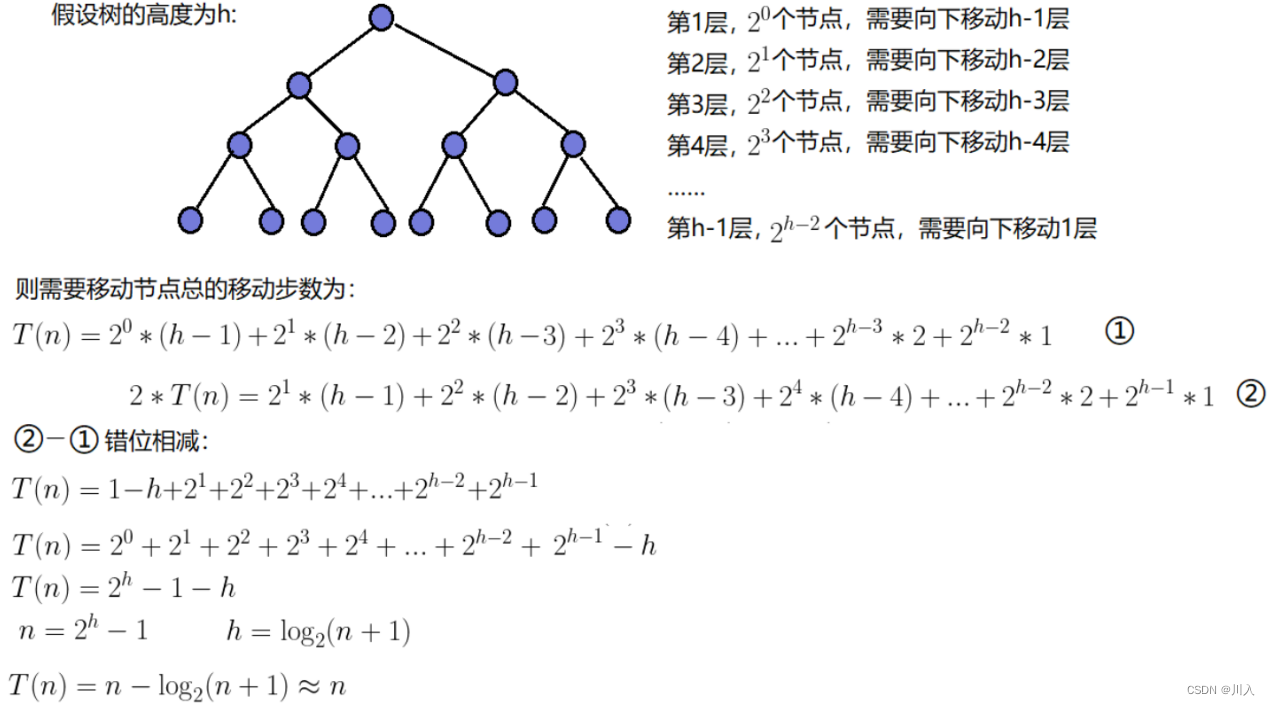
而直接建堆法时间复杂度O(logn),其根本是利用向下建堆实现。
for (int i = (size - 1 - 1) / 2; i >= 0; i--)
{ADjustDown(nums, i);
}class Solution
{
public:// 向下建堆void adjustDown(vector<int> &nums, int parent){int child = parent * 2 + 1;while (child < nums.size()){if (child + 1 < nums.size() && nums[child + 1] > nums[child]){child++;}if (nums[child] > nums[parent]){swap(nums[child], nums[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}// 堆排序的TOP-k问题vector<int> smallestK(vector<int> &arr, int k){vector<int> nums;nums.reserve(k);// 前K个元素来建堆for (int i = 0; i < k; i++){nums.push_back(arr[i]);}for(int i = (k - 1 - 1) / 2; i >= 0; i--){adjustDown(nums, i);}// 对比堆顶元素if (k != 0){for (int i = k; i < arr.size(); i++){if (arr[i] < nums[0]){nums[0] = arr[i];adjustDown(nums, 0);}}}return nums;}
};相关文章:

【C++习题集】-- 堆
(用于复习) 目录 树概念及结构 名词概念 二叉树概念及结构 特殊的二叉树 满二叉树 完全二叉树 运算性质 二叉树存储结构 顺序存储 链式存储 堆 - 顺序存储 堆的性质 堆的实现 堆的应用 堆排序 直接建堆法 树概念及结构 概念:…...

vue + vue-office 实现多种文件(docx、excel、pdf)的预览
支持多种文件( docx、excel、pdf)预览的vue组件库,支持vue2/3。也支持非Vue框架的预览。 github: 《仓库地址》 演 示: 《演示效果》 功能特色 一站式:提供docx、pdf、excel多种文档的在线预览方案,有它就够了简单:…...

30.Netty源码服务端启动主要流程
highlight: arduino-light 服务端启动主要流程 •创建 selector •创建 server socket channel •初始化 server socket channel •给 server socket channel 从 boss group 中选择一个 NioEventLoop •将 server socket channel 注册到选择的 NioEventLoop 的 selector •…...
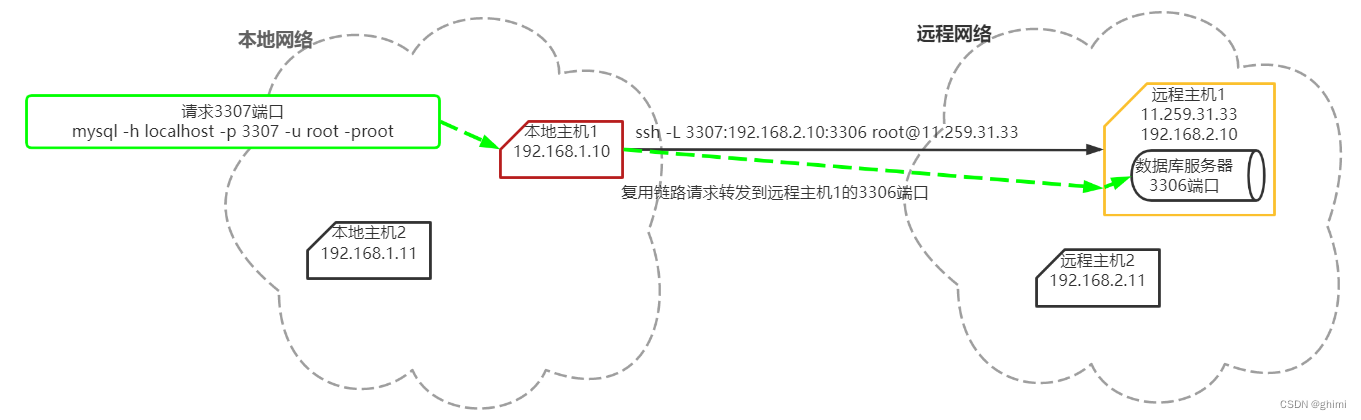
ssh端口转发
在本地客户端操作: ssh远程连接一段时间会失效的问题 vim /etc/ssh_config或vim /etc/ssh/ssh_config 在末尾添加ServerAliveInterval 30,意思是30s会发送一次向服务器连接的请求,以保持会话始终在线 验证: 放一段时间不操作,…...
独立站SEO是什么意思?自主网站SEO的含义?
什么是独立站SEO优化?自建站搜索引擎优化是指什么? 独立站SEO,作为网络营销的重要一环,正在逐渐引起人们的关注。在当今数字化时代,独立站已经成为许多企业、个人宣传推广的首选平台之一。那么,究竟什么是…...

Android JNI系列详解之NDK和JNI介绍
一、前提 针对自己在Android JNI和NDK这块技术的空白知识点,进行这个JNI系列的学习,记录这一阶段的学习。学习的主要步骤:从概念原理解析--->边学边实战--->从易到难,循序渐进。(学习这一阶段的前提:需要有Android开发基础) 学完JNI-NDK开发系列,达到的目的有:…...

LeetCode //C - 20. Valid Parentheses
20. Valid Parentheses Given a string s containing just the characters ‘(’, ‘)’, ‘{’, ‘}’, ‘[’ and ‘]’, determine if the input string is valid. An input string is valid if: Open brackets must be closed by the same type of brackets.Open bracke…...
浅析Java设计模式之四策略模式
title: 浅析Java设计模式之四策略模式 date: 2018-12-29 17:26:17 categories: 设计模式 description: 浅析Java设计模式之四策略模式 1. 目录 1. 目录2. 概念 2.1. 应用场景2.2. 优缺点 2.2.1. 优点2.2.2. 缺点 3. 模式结构4. 样例 4.1. 定义策略4.2. 定义具体策略4.3. 定义…...
基于Spring Boot的餐厅订餐网站的设计与实现(Java+spring boot+MySQL)
获取源码或者论文请私信博主 演示视频: 基于Spring Boot的餐厅订餐网站的设计与实现(Javaspring bootMySQL) 使用技术: 前端:html css javascript jQuery ajax thymeleaf 微信小程序 后端:Java springbo…...
评估指标代码实现)
【图像分割】理论篇(1)评估指标代码实现
图像分割是计算机视觉中的重要任务,用于将图像中的不同区域分割成具有语义意义的区域。以下是几种常用的图像分割评价指标以及它们的代码实现示例(使用Python和常见的计算机视觉库): 1. IoU (Intersection over Union) 与目标检…...

Git checkout 某个版本到指定文件夹下
文章目录 场景说明方案一:git archive 最简单省事方案二:git show 最灵活, 但文件较多时麻烦方案三:git --work-tree 有bug 场景说明 我不想checkout到覆盖本地工作区的文件, 而是想把该版本checkout到另外一个文件夹下ÿ…...
)
Java多态详解(2)
向上转型和向下转型 向上转型 定义:实际就是创建一个子类对象,将其当作父类对象来使用。 语法格式:父类类型 对象名 new 子类类型() Animal animal new Cat("元宝", 2); animal是父类类型,但是可以引用子…...
Camtasia导入srt字幕乱码
我们在使用camtasia制作视频项目时,有时为了用户体验需要导入srt格式的字幕文件,在操作无误的情况下,一顿操作猛如虎之后字幕顺利的导入到软件中了,但字幕却出现了乱码的现象。如下图所示: 如何解决srt乱码问题呢&…...
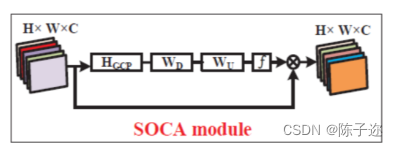
YOLOv5、YOLOv8改进:SOCA注意力机制
目录 简介 2.YOLOv5使用SOCA注意力机制 2.1增加以下SOCA.yaml文件 2.2common.py配置 2.3yolo.py配置 简介 注意力机制(Attention Mechanism)源于对人类视觉的研究。在认知科学中,由于信息处理的瓶颈,人类会选择性地关注所有…...

机器人的运动范围
声明 该系列文章仅仅展示个人的解题思路和分析过程,并非一定是优质题解,重要的是通过分析和解决问题能让我们逐渐熟练和成长,从新手到大佬离不开一个磨练的过程,加油! 原题链接 机器人的运动范围https://leetcode.c…...
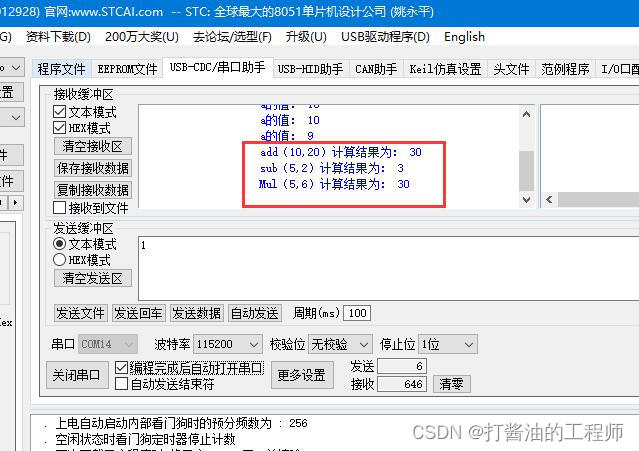
学习笔记|基于Delay实现的LED闪烁|模块化编程|SOS求救灯光|STC32G单片机视频开发教程(冲哥)|第六集(下):实现LED闪烁
文章目录 2 函数的使用1.函数定义(需要带类型)2.函数声明(需要带类型)3.函数调用 3 新建文件,使用模块化编程新建xxx.c和xxx.h文件xxx.h格式:调用头文件验证代码调用:完整的文件结构如下&#x…...
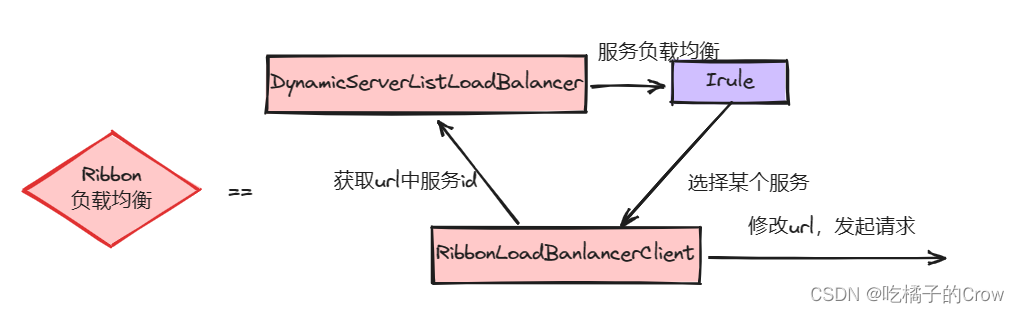
微服务-Ribbon(负载均衡)
负载均衡的面对多个相同的服务的时候,我们选择一定的策略去选择一个服务进行 负载均衡流程 Ribbon结构组成 负载均衡策略 RoundRobinRule:简单的轮询服务列表来选择服务器AvailabilityFilteringRule 对两种情况服务器进行忽略: 1.在默认情…...
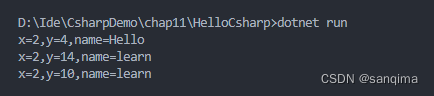
解决C#报“MSB3088 未能读取状态文件*.csprojAssemblyReference.cache“问题
今天在使用vscode软件C#插件,编译.cs文件时,发现如下warning: 图(1) C#报cache没有更新 出现该warning的原因:当前.cs文件修改了,但是其缓存文件*.csprojAssemblyReference.cache没有更新,需要重新清理一下工程&#x…...
GeoScene Pro在地图制图当中的应用
任何地理信息系统建设过程中,背景地图的展示效果对整个系统功能的实现没有直接影响;但是地图的好看与否,会间接的决定着整个项目的高度。 一幅精美的地图不仅能令人赏心悦目、眼前一亮,更能将人吸引到你的系统中,更愿意…...

国标混凝土结构设计规范的混凝土本构关系——基于python代码生成
文章目录 0. 背景1. 代码2. 结果测试 0. 背景 最近在梳理混凝土塔筒的计算指南,在求解弯矩曲率关系以及MN相关曲线时,需要混凝土的本构关系作为输入条件。 1. 代码 这段代码还是比较简单的。不过需要注意的是,我把受拉和受压两种状态统一了…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

