深入浅出Pytorch函数——torch.nn.init.xavier_normal_
分类目录:《深入浅出Pytorch函数》总目录
相关文章:
· 深入浅出Pytorch函数——torch.nn.init.calculate_gain
· 深入浅出Pytorch函数——torch.nn.init.uniform_
· 深入浅出Pytorch函数——torch.nn.init.normal_
· 深入浅出Pytorch函数——torch.nn.init.constant_
· 深入浅出Pytorch函数——torch.nn.init.ones_
· 深入浅出Pytorch函数——torch.nn.init.zeros_
· 深入浅出Pytorch函数——torch.nn.init.eye_
· 深入浅出Pytorch函数——torch.nn.init.dirac_
· 深入浅出Pytorch函数——torch.nn.init.xavier_uniform_
· 深入浅出Pytorch函数——torch.nn.init.xavier_normal_
· 深入浅出Pytorch函数——torch.nn.init.kaiming_uniform_
· 深入浅出Pytorch函数——torch.nn.init.kaiming_normal_
· 深入浅出Pytorch函数——torch.nn.init.trunc_normal_
· 深入浅出Pytorch函数——torch.nn.init.orthogonal_
· 深入浅出Pytorch函数——torch.nn.init.sparse_
torch.nn.init模块中的所有函数都用于初始化神经网络参数,因此它们都在torc.no_grad()模式下运行,autograd不会将其考虑在内。
根据Glorot, X.和Bengio, Y.在《Understanding the difficulty of training deep feedforward neural networks》中描述的方法,用一个正态分布生成值,填充输入的张量或变量。结果张量中的值采样自 N ( 0 , std 2 ) N(0, \text{std}^2) N(0,std2)的正态分布,其中标准差:
std = gain × 2 fan_in + fan_put \text{std}=\text{gain}\times\sqrt{\frac{2}{\text{fan\_in}+\text{fan\_put}}} std=gain×fan_in+fan_put2
这种方法也被称为Glorot initialisation。
语法
torch.nn.init.xavier_normal_(tensor, gain=1.0)
参数
tensor:[Tensor] 一个 N N N维张量torch.Tensorgain:[float] 可选的缩放因子
返回值
一个torch.Tensor且参数tensor也会更新
实例
w = torch.empty(3, 5)
nn.init.xavier_normal_(w)
函数实现
def xavier_normal_(tensor: Tensor, gain: float = 1.) -> Tensor:r"""Fills the input `Tensor` with values according to the methoddescribed in `Understanding the difficulty of training deep feedforwardneural networks` - Glorot, X. & Bengio, Y. (2010), using a normaldistribution. The resulting tensor will have values sampled from:math:`\mathcal{N}(0, \text{std}^2)` where.. math::\text{std} = \text{gain} \times \sqrt{\frac{2}{\text{fan\_in} + \text{fan\_out}}}Also known as Glorot initialization.Args:tensor: an n-dimensional `torch.Tensor`gain: an optional scaling factorExamples:>>> w = torch.empty(3, 5)>>> nn.init.xavier_normal_(w)"""fan_in, fan_out = _calculate_fan_in_and_fan_out(tensor)std = gain * math.sqrt(2.0 / float(fan_in + fan_out))return _no_grad_normal_(tensor, 0., std)
相关文章:

深入浅出Pytorch函数——torch.nn.init.xavier_normal_
分类目录:《深入浅出Pytorch函数》总目录 相关文章: 深入浅出Pytorch函数——torch.nn.init.calculate_gain 深入浅出Pytorch函数——torch.nn.init.uniform_ 深入浅出Pytorch函数——torch.nn.init.normal_ 深入浅出Pytorch函数——torch.nn.init.c…...

Abandon_Ubuntu Declaration
鉴于以下几个原因,持续到明年考研结束,我将不再捣鼓ubuntu和任何linux系统, 原因如下: ubuntu23.04不支持wps编辑pdf这个核心功能,且开机向canonial公司发送远程遥测,暂时不会用iptables禁用,故…...

Java设计模式-抽象工厂模式
简介 设计模式是软件设计中的一种常见方法,通过定义一系列通用的解决方案,来解决常见的软件设计问题。其中,抽象工厂模式是一种非常常见的设计模式,它可以帮助我们创建一组相关的对象,而不需要指定具体的实现方式。 …...

Rust语法:所有权引用生命周期
文章目录 所有权垃圾回收管理内存手动管理内存Rust的所有权所有权转移函数所有权传递 引用与借用可变与不可变引用 生命周期悬垂引用函数生命周期声明结构体的生命周期声明Rust生命周期的自行推断生命周期约束静态生命周期 所有权 垃圾回收管理内存 Python,Java这…...
办手机卡/流量卡需要问清楚啥?
网上的手机卡一搜能出现千千万,那么怎么才能避免购买到那些套路卡呢?今天就给大家分享一下,办理手机卡时需要问清楚什么? 办理流量卡需要咨询的五大问题,下面开始进入正题。 1、是否是正规号卡?正规的号…...

vim基本使用方法
VIM 1.vim介绍2.vim基本操作2.1 模式切换2.2 命令模式2.3 底行模式 1.vim介绍 vim是linux上一个有多个编辑模式的编辑器。 这里主要介绍三种模式: 命令模式(Normal mode) 执行命令的模式,主要任务就是控制光标移动、复制和删除。…...
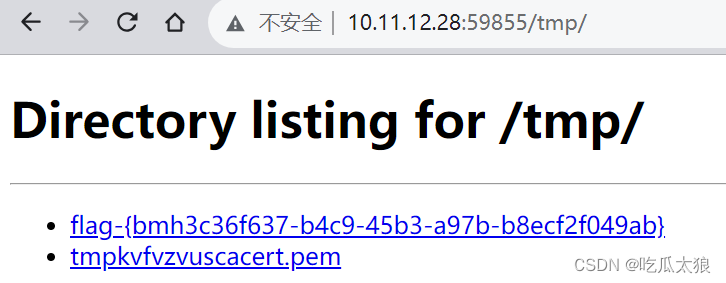
漏洞指北-VulFocus靶场专栏-入门
漏洞指北-VulFocus靶场01-入门 VulFocus靶场前置条件:入门001 命令执行漏洞step1: 输入默认index的提示step2: 入门002 目录浏览漏洞step1:进入默认页面,找到tmp目录step2 进入tmp目录获取flag文件 VulFocus靶场前置条…...

管理类联考——逻辑——真题篇——按知识分类——汇总篇——二、论证逻辑——推论——第二节——数字推理题
文章目录 第二节 数字推理题真题(2017-31)——推论——数字推理题——数量比例模型真题(2014-33)——推论——数字推理题——数量比例模型——(1)若题干既有数量,也有比例,答案一般为数量。(2)若题干只有比例没有数量,答案一般为比例。真题(2018-44)——推论——数…...
 git reflog查看引用日志)
git基础教程(24) git reflog查看引用日志
文章目录 1、`git reflog`命令说明2、`git reflog`命令显示内容3、具体的用法4、引起ref变化的操作有git reflog 命令是用来恢复本地错误操作很重要的一个命令,所以在这里对它进行一下整理。 1、git reflog命令说明 reflog翻译:Reference logs(参考日志) git reflog命令:…...
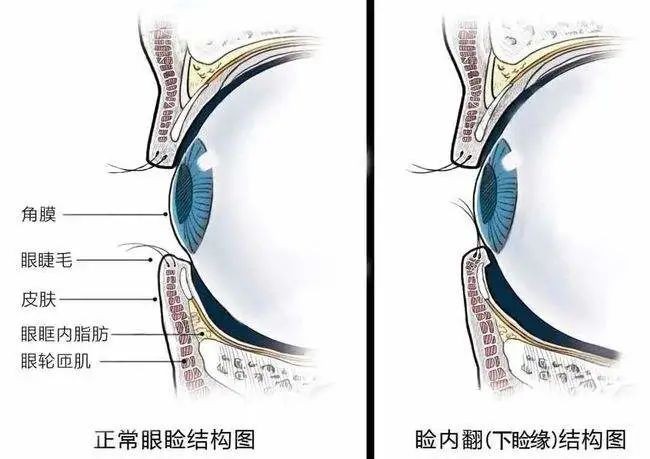
成都爱尔谭娇主任提醒孩子不停揉眼睛是因为什么
孩子总是揉眼睛, 明显眼睛不舒服, 但看着好像没什么? 可孩子不停眨眼流泪, 肯定不对…… 孩子到底怎么了? 孩子可能长了“倒睫”! 孩子出现倒睫毛就是睫毛不朝外长而向内长,是婴幼儿很容易患的一种眼病。 由于孩子的脸颊及鼻梁发…...

医疗设备管理软件哪家好?医院设备全生命周期管理要怎么做?
随着医学技术的不断进步,医疗设备变得越来越先进,越来越复杂。因此,医疗设备的管理也变得越来越重要。传统的医疗设备管理方式存在很多问题,比如设备数据难统计、报修方式难统一、巡检维保难规范等。为了解决这些问题,…...
基于PaddlePaddle实现的声纹识别系统
前言 本项目使用了EcapaTdnn、ResNetSE、ERes2Net、CAM等多种先进的声纹识别模型,不排除以后会支持更多模型,同时本项目也支持了MelSpectrogram、Spectrogram、MFCC、Fbank等多种数据预处理方法,使用了ArcFace Loss,ArcFace loss…...
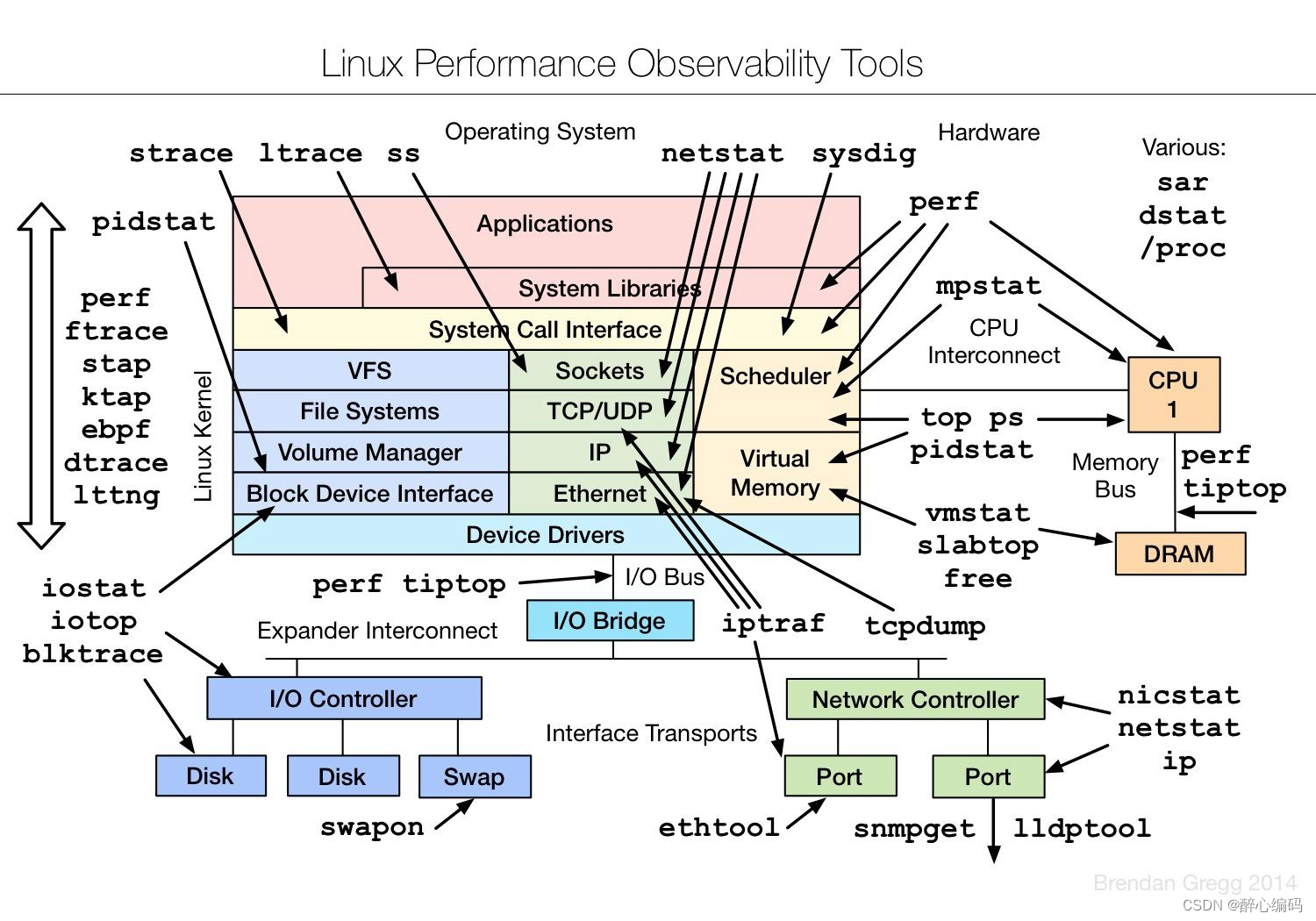
使用GDB工具分析core文件的方法
引言: 在软件开发过程中,我们经常会遇到程序崩溃或异常退出的情况。这时,一个非常有用的工具就是GDB(GNU调试器),它可以帮助我们分析core文件并找出导致程序崩溃的原因。本文将介绍如何使用GDB工具来分析c…...

Maven - 统一构建规范:Maven 插件管理最佳实践
文章目录 Available Plugins开源项目中的使用插件介绍maven-jar-pluginmaven-assembly-pluginmaven-shade-pluginShade 插件 - 标签artifactSetrelocationsfilters 完整配置 Available Plugins https://maven.apache.org/plugins/index.html Maven 是一个开源的软件构建工具&…...

对接海康明眸门禁设备-删除人员信息
对接海康明眸门禁设备-删除人员信息 文中登录 退出登录 长连接和海康hCNetSDK等接口 见文章 初始SDK和登录 /*** 删除人脸 IotCommDataResult 自定义类 收集结果*/Overridepublic List<IotCommDataResult> deleteFace(IotCameraParam camera, Collection<Long> us…...
LEADTOOLS Imaging SDK Crack
LEADTOOLS Imaging SDK Crack 高级开发人员工具包包括ActiveX和WPF/XAML控件。 LEADTOOLS Imaging SDK为文件格式导入/导出、图像压缩、图像显示和效果、颜色转换、图像处理、TWAIN扫描、图像通用对话框、数据库集成、打印和互联网提供了基本和高级的彩色图像功能。 LEADTOOLS …...

2023并发之八股文——面试题
基础知识 并发编程的优缺点为什么要使用并发编程(并发编程的优点) 充分利用多核CPU的计算能力:通过并发编程的形式可以将多核CPU 的计算能力发挥到极致,性能得到提升方便进行业务拆分,提升系统并发能力和性能&#x…...

操作记录日志保存设计实现
定义一个切面类 @Aspect @Slf4j @Component @RequiredArgsConstructor public class OperateLogAopConfig {private final ISysOperateLogService sysOperateLogService;@Around("@annotation(operateLog)")public Object operateLog(ProceedingJoinPoint point, Op…...

PL 侧驱动和fpga 重加载的方法
可以解决很多的问题 时钟稳定后加载特定fpga ip (要不内核崩的一塌糊涂)fpga 稳定复位软件决定fpga ip 加载的时序 dluash load /usr/local/scripts/si5512_setup.lua usleep 30 mkdir -p /lib/firmware cp -rf /usr/local/firmare/{*.bit.bin,*.dtbo} …...
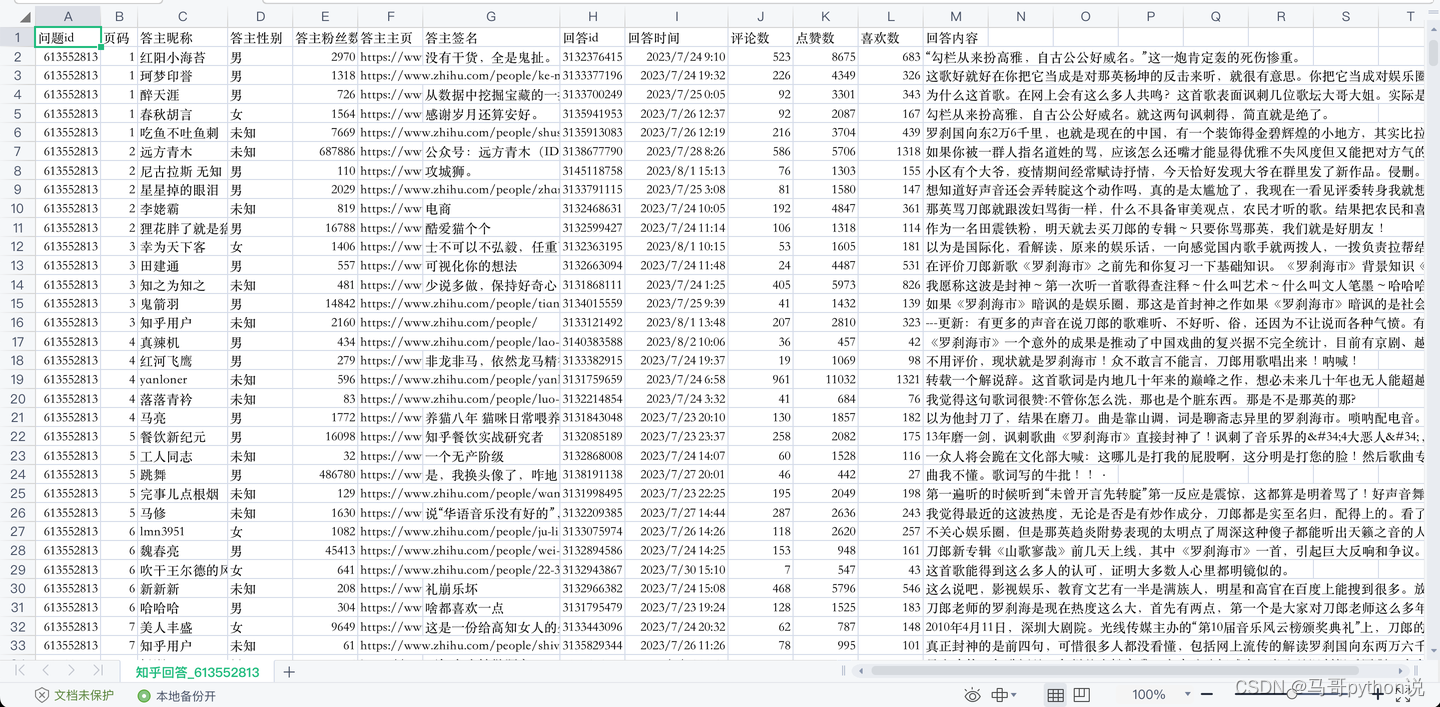
【2023最新爬虫】用python爬取知乎任意问题下的全部回答
老规矩,先上结果: 爬取了前200多页,每页5条数据,共1000多条回答。(程序设置的自动判断结束页,我是手动break的) 共爬到13个字段,包含: 问题id,页码,答主昵称,答主性别,…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...
