【开源三方库】bignumber.js:一个大数数学库
OpenHarmony(OpenAtom OpenHarmony简称“OpenHarmony”)三方库,是经过验证可在OpenHarmony系统上可重复使用的软件组件,可帮助开发者快速开发OpenHarmony应用。如果是发布到开源社区,称为开源三方库,开发者可以通过访问开源社区获取。接下来我们来了解bignumber.js开源三方库。
bignumber.js是一个数学库,用于任意精度十进制和非十进制算术的 JavaScript 库。
特点
- 整数和小数。
- 简单的 API,但功能齐全。
- 比Java的BigDecimal JavaScript版本更快,更小,也许更容易使用。
- 8 KB 缩小和压缩。
- 复制 JavaScript 的 Number 类型的 、 和 方法toExponential、toFixed、toPrecision、toString。
- 包括一个和正确舍入的方法toFraction squareRoot。
- 支持加密安全的伪随机数生成。
- 无依赖关系。
- 广泛的平台兼容性:仅使用 JavaScript 1.5 (ECMAScript 3) 功能。
使用场景
JavaScript因为存在计算的精度问题,所以直接计算就可能会导致各种各样的bug,为了解决这个问题,就可以使用BigNumber.js这个库。它的大概原理是将所有数字当做字符串,重新实现了计算逻辑。
使用示例
- 安装bignumber.js
ohpm install bignumber.js
OpenHarmony ohpm 环境配置等更多内容,请参考如何安装 OpenHarmony ohpm 包
- 导入bignumber.js
import BigNumber from "bignumber.js";
- 调用接口
let x = new BigNumber(123.4567);
let y = BigNumber('123456.7e-3');
let z = new BigNumber(x);
expect(x).assertEqual(y);
expect(y).assertEqual(z);
expect(x).assertEqual(z);
该库导出单个构造函数 BigNumber,该函数接受 Number、String 或 BigNumber 类型的值。
let x = new BigNumber('1111222233334444555566');
x.toString(); // "1.111222233334444555566e+21"
x.toFixed(); // "1111222233334444555566"
要获取BigNumber的字符串值,请使用toString()或toFixed()。
//使用超过15个有效数字的数字文字会导致精度损失。
new BigNumber(1.0000000000000001) // '1'
new BigNumber(88259496234518.57) // '88259496234518.56'
new BigNumber(99999999999999999999) // '100000000000000000000'
//使用数值范围之外的数字文字会导致精度损失。
new BigNumber(2e+308) // 'Infinity'
new BigNumber(1e-324) // '0'
//Number值的算术运算的意外结果导致精度损失。
new BigNumber(0.7 + 0.1) // '0.7999999999999999'
如果不太了解数字值的有限精度,建议从字符串值而不是数字值创建 BigNumbers,以避免潜在的精度损失。
new BigNumber(Number.MAX_VALUE.toString(2), 2)
从数字创建大数时,请注意,大数是从数字的十进制值创建的,而不是从其基础二进制值创建的。如果需要后者,则传递 Number 的值并指定基数 2.toString()或toString(2)。
a = new BigNumber(1011, 2) // "11"
b = new BigNumber('zz.9', 36) // "1295.25"
c = a.plus(b)
可以从 2 到 36 的基数中的值创建大数字。请参阅ALPHABET以扩展此范围。
0.3 - 0.1 // 0.19999999999999998
x = new BigNumber(0.3)
x.minus(0.1) // "0.2"
x // "0.3"
如果未为十进制值指定基数 10,则性能更好。仅当要将输入值的小数位数限制为当前INK http://mik设置时,才指定基数 10。BigNumber 是不可变的,因为它不会被其方法更改。
x.dividedBy(y).plus(z).times(9)
x.times('1.23456780123456789e+9').plus(9876.5432321).dividedBy('4444562598.111772').integerValue() // "0.3"
返回 BigNumber 的方法可以链接。
x = new BigNumber(255.5)
x.toExponential(5) // "2.55500e+2"
x.toFixed(5) // "255.50000"
x.toPrecision(5) // "255.50"
x.toNumber() // 255.5
BigNumber与JavaScript的Number类型一样,有toExponential,toFixed和toPrecision方法。
x.toString(16) // "ff.8"
可以为toString指定基数。
如果没有指定基数10,即使用toString()而不是toString(10),则性能会更好。如果要将字符串的小数位数限制为当前的DECIMAL_PLACES设置,请仅指定基数10。
y = new BigNumber('1234567.898765')
y.toFormat(2) // "1,234,567.90"
有一种toFormat方法可能对国际化有用。
y = new BigNumber(355)
pi = y.dividedBy(113) // "3.1415929204"
pi.toFraction() // [ "7853982301", "2500000000" ]
pi.toFraction(1000) // [ "355", "113" ]
有一个toFraction方法,它有一个可选的最大分母参数。
x = new BigNumber(NaN) // "NaN"
y = new BigNumber(Infinity) // "Infinity"
x.isNaN() && !y.isNaN() && !x.isFinite() && !y.isFinite()
以及isNaN和isFinite方法,因为和是有效值。NaN、Infinity、BigNumber。
x = new BigNumber(-123.456);
x.c // [ 123, 45600000000000 ] coefficient (i.e. significand)
x.e // 2 exponent
x.s // -1 sign
BigNumber的值以系数、指数和符号的十进制浮点格式存储。
//为原始BigNumber构造函数设置DECIMAL_LACES
BigNumber.set({ DECIMAL_PLACES: 10 })
// 创建另一个BigNumber构造函数,可选地传入配置对象
BN = BigNumber.clone({ DECIMAL_PLACES: 5 })
x = new BigNumber(1)
y = new BN(1)
x.div(3) // '0.3333333333'
y.div(3) // '0.33333'
为了高级使用,可以创建多个BigNumber构造函数,每个构造函数都有自己的独立配置。
源码地址&ohpm仓地址
以上就是bignumber.js的一些基本介绍,更多详情可以前往源码地址或者ohpm仓地址参考bignumber.js文档。
参考资料
如何安装 OpenHarmony ohpm 包:
bignumber.js API:
源码地址:
ohpm地址:
点击关注阅读原文,了解更多资讯
相关文章:

【开源三方库】bignumber.js:一个大数数学库
OpenHarmony(OpenAtom OpenHarmony简称“OpenHarmony”)三方库,是经过验证可在OpenHarmony系统上可重复使用的软件组件,可帮助开发者快速开发OpenHarmony应用。如果是发布到开源社区,称为开源三方库,开发者…...

【C++】iota函数 + sort函数实现基于一个数组的多数组对应下标绑定排序
目录 一、iota函数 1. 函数解析 ① 迭代器类型(补充) ② 头文件 ③ 参数 2. 函数用途与实例 二、sort函数 1、 函数解读 2、实现倒序排列 2.1 greater 与 less 模板参数 2.2 lambda表达式 三、下标绑定排序(zip) --- 833.字符串中的查找与替换 一、…...

C# window forms 进度条实现
在 C# Windows Forms 应用程序中,如果在后台执行长时间运行的任务,并希望同时更新进度条,可以使用多线程来实现。这将确保进度条的更新不会阻塞主线程,从而保持界面的响应性。以下是一个示例,演示了如何在后台执行任务…...

ListNode相关
目录 2. 链表相关题目 2.1 合并两个有序链表(简单):递归 2.2 删除排序链表中的重复元素(简单):一次遍历 2.3 两链表相加(中等):递归 2.4 删除链表倒数第N个节点&…...
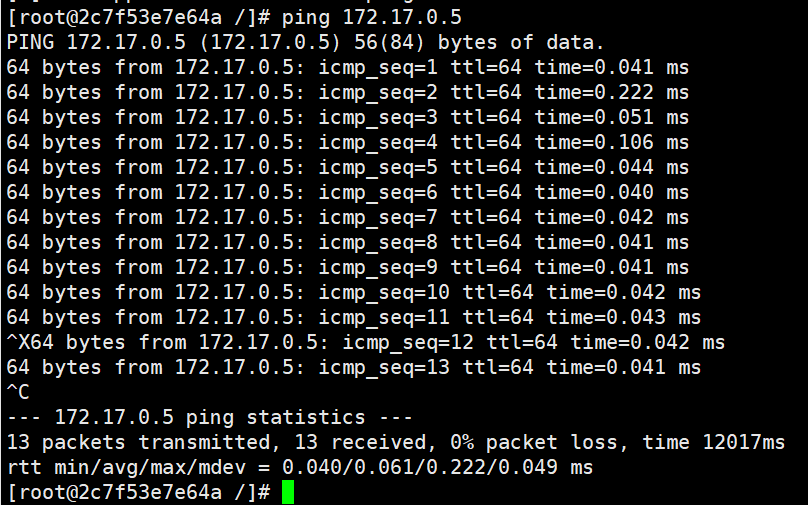
docker的资源控制及docker数据管理
目录 一.docker的资源控制 1.CPU 资源控制 1.1 资源控制工具 1.2 cgroups有四大功能 1.3 设置CPU使用率上限 1.4 进行CPU压力测试 1.5 设置50%的比例分配CPU使用时间上限 1.6 设置CPU资源占用比(设置多个容器时才有效) 1.6.1 两个容器测试cpu 2&…...
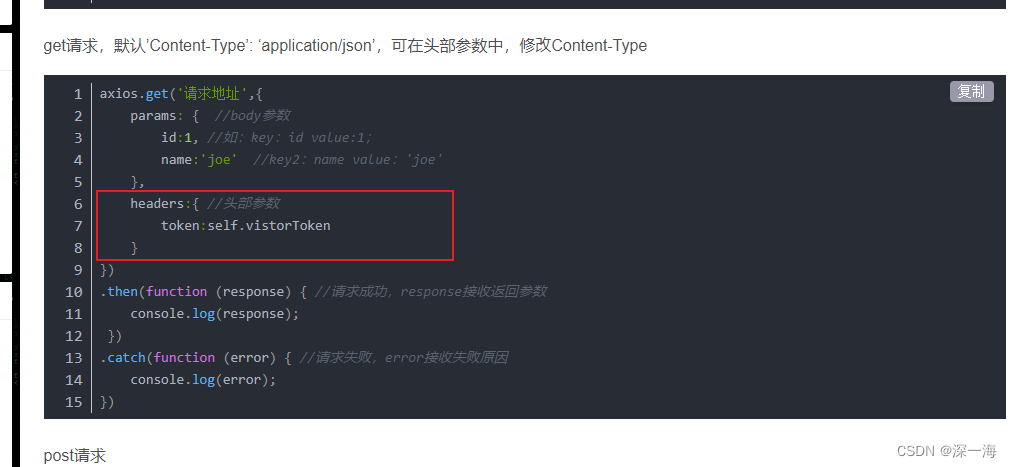
通过请求头传数据向后端发请求
axios (get post请求、头部参数添加)傻瓜式入门axios_axiospost请求参数_web_blog的博客-CSDN博客...
产品流程图是什么?怎么做?
产品流程图是什么? 产品流程图是一种图形化的表达方式,用于描述产品开发、制造、销售、使用等各个阶段中涉及的流程、步骤和关系。它通过图形符号、箭头、文本等元素,展示了产品的各个环节之间的关联和顺序,通常被用于可视化产…...

面试之快速学习STL-map
关联式容器 包括 map、multimap、set 以及 multiset 这 4 种容器。和序列式容器区别: a . 关联式容器在存储元素时还会为每个元素在配备一个键,整体以键值对的方式存储到容器中。 b . 相比前者,关联式容器可以通过键值直接找到对应的元素&am…...
ES的索引结构与算法解析
提到ES,大多数爱好者想到的都是搜索引擎,但是明确一点,ES不等同于搜索引擎。不管是谷歌、百度、必应、搜狗为代表的自然语言处理(NLP)、爬虫、网页处理、大数据处理的全文搜索引擎,还是有明确搜索目的的搜索行为,如各大…...

32.Netty源码之服务端如何处理客户端新建连接
highlight: arduino-light 服务端如何处理客户端新建连接 Netty 服务端完全启动后,就可以对外工作了。接下来 Netty 服务端是如何处理客户端新建连接的呢? 主要分为四步: md Boss NioEventLoop 线程轮询客户端新连接 OP_ACCEPT 事件ÿ…...

代码随想录day11
20. 有效的括号 ● 力扣题目链接 ● 给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串,判断字符串是否有效。 ● 有效字符串需满足: ● 左括号必须用相同类型的右括号闭合。 ● 左…...

RabbitMQ实习面试题
RabbitMQ实习面试题 在 RabbitMQ 中,确保生产者消息正确发布以及确保消费者已经消费是非常重要的任务。以下是一些方法和策略,可以帮助您在 RabbitMQ 中实现这些目标: 确保生产者消息正确发布: 持久化消息:将消息设…...
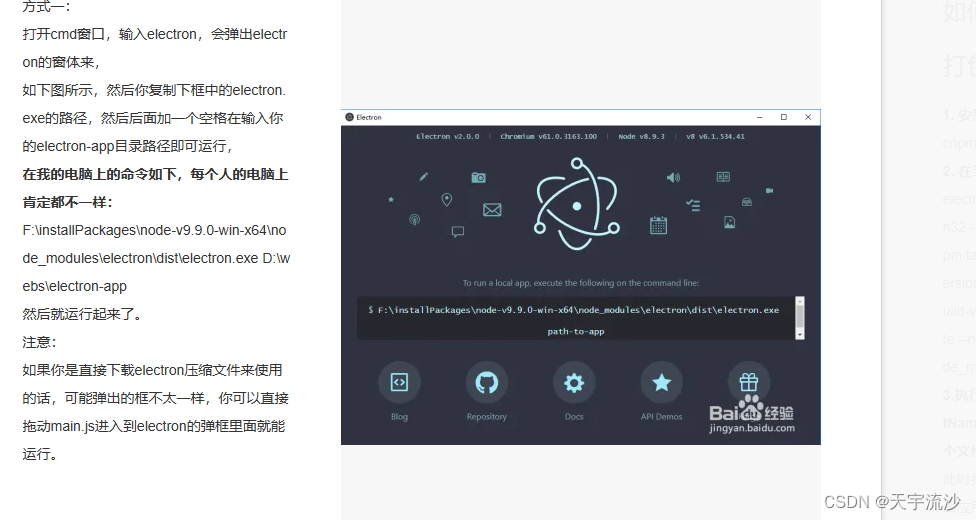
Electron入门,项目运行,只需四步轻松搞定。
electron 简单介绍: 实现:HTML/CSS/JS桌面程序,搭建跨平台桌面应用。 electron 官方文档: [https://electronjs.org/docs] 本文是基于以下2篇文章且自行实践过的,可行性真实有效。 文章1: https://www.cnbl…...
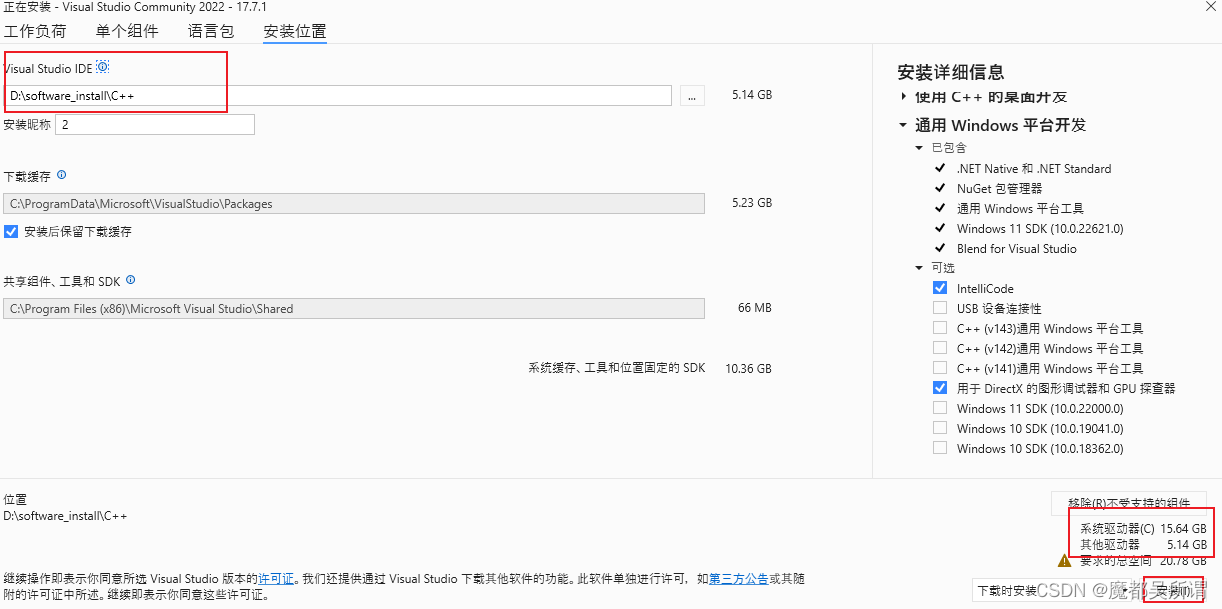
【C++】visualstudio环境安装
记录了部分安装步骤,可能有点不全,参考下,需要的磁盘空间差不多20GB; 下载 https://visualstudio.microsoft.com/zh-hans/vs/ 下载完成: 双击进入安装状态: 根据自己的需求勾选安装项: 选择…...
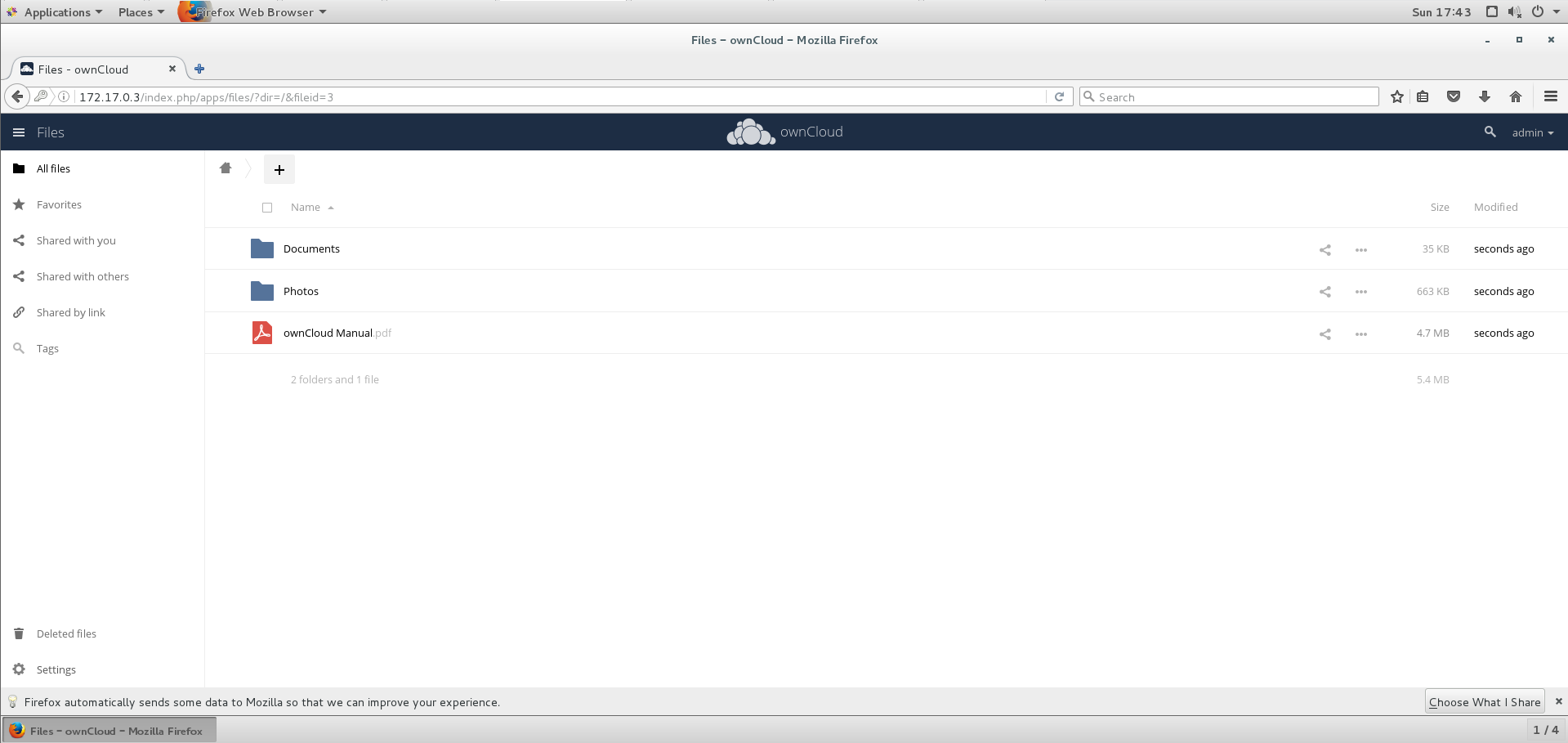
使用MySQL:5.6和owncloud镜像搭建个人网盘
拉取镜像 [rootkvm ~]# docker pull mysql:5.6[rootkvm ~]# docker pull owncloud启动mysql容器 [rootkvm ~]# docker run -d --name db1 -e MYSQL_ROOT_PASSWORDroot mysql:5.6 db832e4e4333a0e9a7c152a67272721fdbe5381054090c5eb24f90455390a852 [rootkvm ~]# docker ps …...

php中创建对象时传递的参数是构造方法
PHP中创建对象时,可以通过构造方法的参数来传递参数值。构造方法是一个特殊的方法,在创建对象时会自动调用,用于进行对象的初始化操作。 以下是一个示例代码,展示了如何在PHP中使用构造方法传递参数: class MyClass …...

C++并发及互斥保护示例
最近要写一个多线程的并发数据库,主要是希望使用读写锁实现库的并发访问,同时考虑到其他平台(如Iar)没有C的读写锁,需要操作系统提供,就将读写锁封装起来。整个过程还是比较曲折的,碰到了不少问题,在此就简…...

新手常犯的错误,anzo capital昂首资本一招避免少走弯路
新手是不是经常交易中赚不到钱,今天anzo capital昂首资本就盘点一下新手常犯的错误,一招教你少走弯路。 一.随便选择交易账户 开立实时账户时选择正确的账户类型,anzo capital昂首资本教你比较所有提供的账户类型,选择最符合财务…...
 前后端 关于时间格式数据的处理方法)
Java Vue (el-date-picker组件) 前后端 关于时间格式数据的处理方法
前端使用 elment-ui 组件 el-date-picker 其中组件需要格式化时间,增加属性 value-format"yyyy-MM-dd" 后端 Java 接收参数类型 后端Dto 使用Date接收,并添加JsonFormat注解 JsonFormat(pattern"yyyy-MM-dd") private Date testTi…...

Python爬虫——scrapy_多条管道下载
定义管道类(在pipelines.py里定义) import urllib.requestclass DangDangDownloadPipelines:def process_item(self, item, spider):url http: item.get(src)filename ../books_img/ item.get(name) .jpgurllib.request.urlretrieve(url, filename…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...
