(搜索) 剑指 Offer 13. 机器人的运动范围 ——【Leetcode每日一题】
❓剑指 Offer 13. 机器人的运动范围
难度:中等
地上有一个 m 行 n 列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于 k 的格子。例如,当 k 为18时,机器人能够进入方格 [35, 37] ,因为3+5+3+7=18。但它不能进入方格 [35, 38],因为 3+5+3+8=19。请问该机器人能够到达多少个格子?
示例 1:
输入:m = 2, n = 3, k = 1
输出:3
示例 2:
输入:m = 3, n = 1, k = 0
输出:1
提示:
1 <= n,m <= 1000 <= k <= 20
💡思路:广度优先搜索
我们将行坐标和列坐标数位之和大于 k 的格子看作障碍物,那么这道题就是一道很传统的搜索题目,我们可以使用广度优先搜索或者深度优先搜索来解决它,本文选择使用 广度优先搜索 的方法来讲解。
那么如何计算一个数的数位之和呢?
- 我们只需要对数
x每次对 10 取余,就能知道数x的个位数是多少,然后再将x除 10,这个操作等价于将 x 的十进制数向右移一位,删除个位数(类似于二进制中的>>右移运算符),不断重复直到x为 0 时结束。
🍁代码:(C++、Java)
C++
class Solution {
private:int getsum(int x){int ans = 0;while(x > 0 ){ans += x % 10;x /= 10;}return ans;}
public:int movingCount(int m, int n, int k) {if(k == 0) return 1;vector<pair<int, int>> dirs{{0, 1}, {1, 0}, {0, -1}, {-1, 0}};queue<pair<int, int>> q;q.push(make_pair(0, 0));vector<vector<int>> visited(m, vector<int>(n));visited[0][0] = 1;int ans = 1;while(!q.empty()){auto [x, y] = q.front();q.pop();for(auto dir : dirs){int cur_x = x + dir.first, cur_y = y + dir.second;if(cur_x < 0 || cur_x >= m || cur_y < 0 || cur_y >= n || visited[cur_x][cur_y] || getsum(cur_x) + getsum(cur_y) > k) continue;q.push(make_pair(cur_x, cur_y));visited[cur_x][cur_y] = 1;ans++;}}return ans;}
};
Java
class Solution {private int getsum(int x){int ans = 0;while(x > 0 ){ans += x % 10;x /= 10;}return ans;}public int movingCount(int m, int n, int k) {if(k == 0) return 1;int[][] dirs = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};Queue<int[]> q = new LinkedList<int[]>();q.offer(new int[]{0, 0});int[][] visited = new int[m][n];visited[0][0] = 1;int ans = 1;while(!q.isEmpty()){int[] cell = q.poll();for(int[] dir : dirs){int cur_x = cell[0] + dir[0], cur_y = cell[1] + dir[1];if(cur_x < 0 || cur_x >= m || cur_y < 0 || cur_y >= n || visited[cur_x][cur_y] == 1 || getsum(cur_x) + getsum(cur_y) > k) continue;q.offer(new int[]{cur_x, cur_y});visited[cur_x][cur_y] = 1;ans++;}}return ans;}
}
🚀 运行结果:
🕔 复杂度分析:
- 时间复杂度: O ( m n ) O(mn) O(mn),其中
m为方格的行数,n为方格的列数。考虑所有格子都能进入,那么搜索的时候一个格子最多会被访问的次数为常数,所以时间复杂度为 O ( 4 m n ) = O ( m n ) O(4mn) = O(mn) O(4mn)=O(mn)。 - 空间复杂度: O ( m n ) O(mn) O(mn),搜索的时候需要一个大小为 O ( m n ) O(mn) O(mn), 的标记结构用来标记每个格子是否被走过。
题目来源:力扣。
放弃一件事很容易,每天能坚持一件事一定很酷,一起每日一题吧!
关注我LeetCode主页 / CSDN—力扣专栏,每日更新!
注: 如有不足,欢迎指正!
相关文章:

(搜索) 剑指 Offer 13. 机器人的运动范围 ——【Leetcode每日一题】
❓剑指 Offer 13. 机器人的运动范围 难度:中等 地上有一个 m 行 n 列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外)&…...
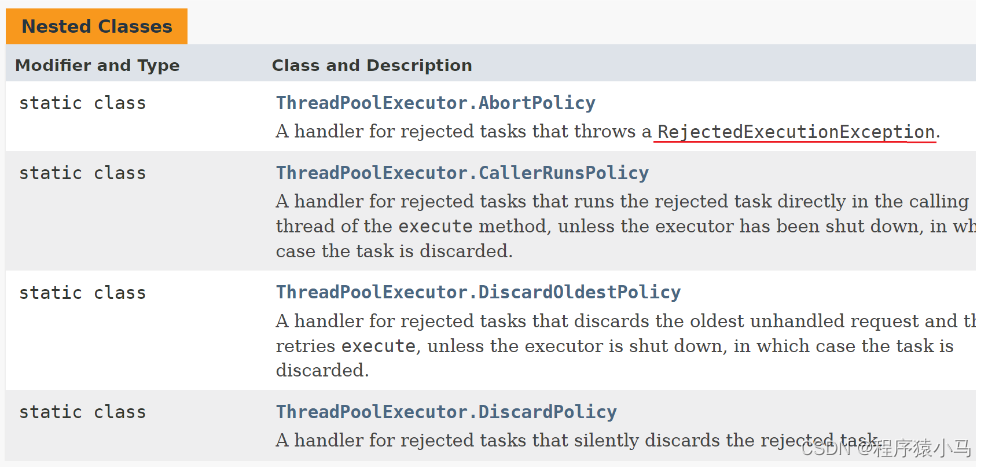
Java并发编程之线程池详解
目录 🐳今日良言:不悲伤 不彷徨 有风听风 有雨看雨 🐇一、简介 🐇二、相关代码 🐼1.线程池代码 🐼2.自定义实现线程池 🐇三、ThreadPoolExecutor类 🐳今日良言:不悲伤 不彷徨 有风听风 有…...

开源数据库Mysql_DBA运维实战 (总结)
开源数据库Mysql_DBA运维实战 (总结) SQL语句都包含哪些类型 DDL DCL DML DQL Yum 安装MySQL的配置文件 配置文件:/etc/my.cnf日志目录:/var/log/mysqld.log错误日志:/var/log/mysql/error.log MySQL的主从切换 查看主…...
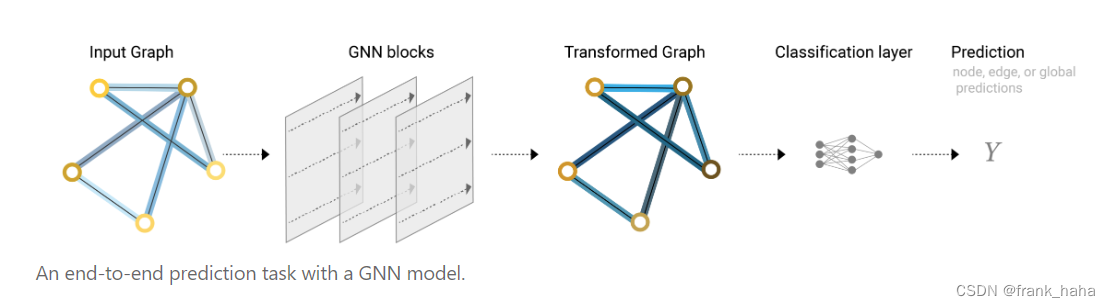
图神经网络与分子表征:1. 分子图和图神经网络基础
CSDN的朋友们大家好,好久没写系列文章了。 近期读了很多图神经网络(GNN)和分子表征(molecular representation)的论文,正好最近不是很忙,所以我决定把自己的学习过程记录下来,与大家…...

Spring Boot与Redisson的整合。分布式锁
Spring Boot与Redisson的整合可以帮助您在Spring Boot应用程序中使用分布式锁、缓存等功能。下面是一些基本步骤来整合Spring Boot与Redisson: 添加Maven/Gradle依赖: 在您的Spring Boot项目的pom.xml(Maven)或build.gradle&#…...

Lua中逻辑运算符and,or,not 区别与用法
在Lua中,逻辑运算符包括 and、or 和 not。它们用于对布尔值进行逻辑运算。 and运算符: 当同时满足两个表达式时,返回第二个表达式的值;否则,返回第一个表达式的值。如果第一个表 达式的值为false或nil,则…...

使用 spaCy 增强 NLP 管道
介绍 spaCy 是一个用于自然语言处理 (NLP) 的 Python 库。SpaCy 的 NLP 管道是免费且开源的。开发人员使用它来创建信息提取和自然语言理解系统,例如 Cython。使用该工具进行生产,拥有简洁且用户友好的 API。 如果您处理大量文本,您会想了解更多相关信息。例如,它是关于什…...
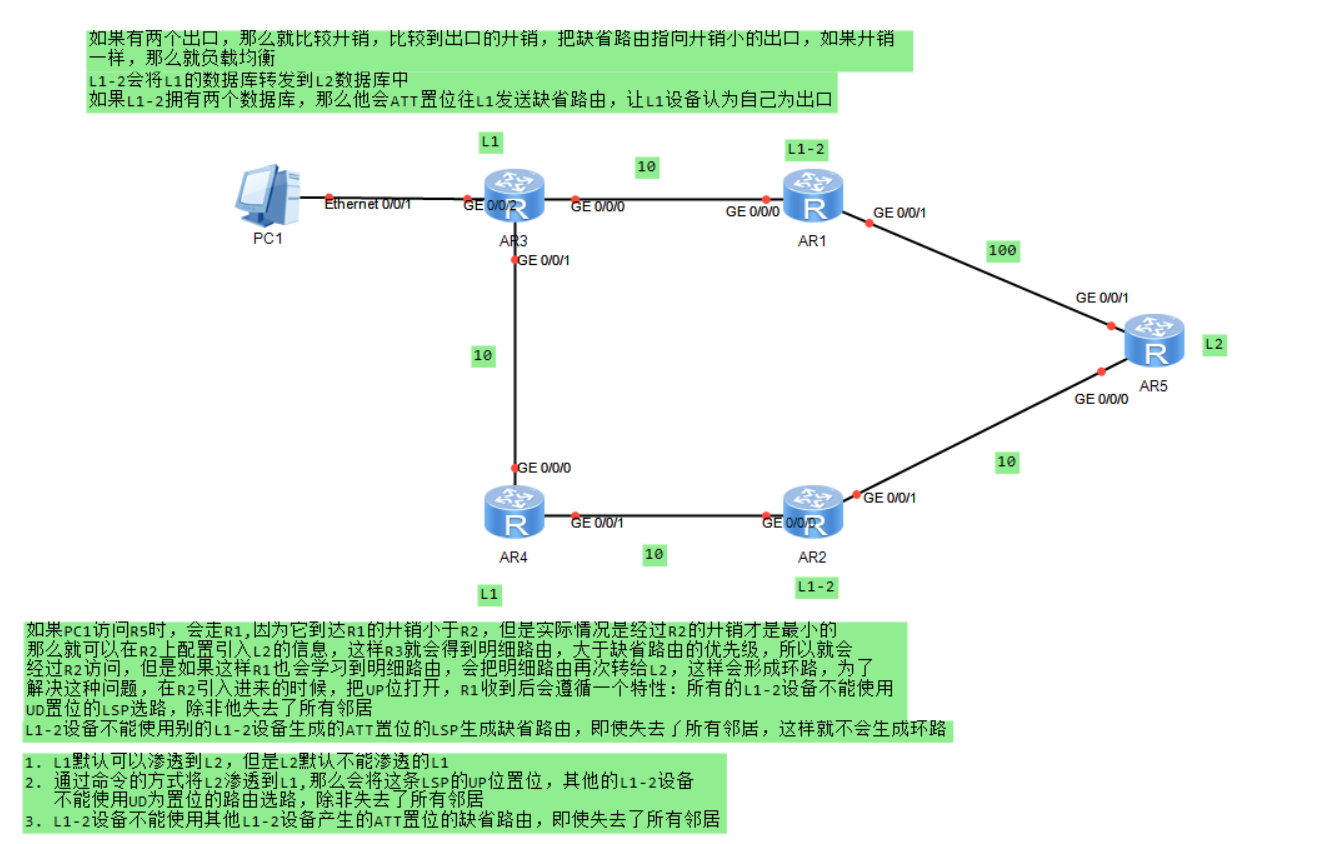
【HCIP】08.ISIS中间系统
链路状态协议,传递LSA信息ISIS基于数据链路层封装在OSI时,也有自己的网络层地址和自己的路由协议,即ISIS。之前的ISIS支持OSI的网络层地址,是为OSI中的CLNP(无连接网络协议)网络设计的路由协议,…...

Android 13 Framework 添加自定义的系统服务CustomService
目的: 添加自定义的系统服务,在自定义的服务中开发定制的API接口和功能,独立于系统核心服务,方便开发和维护。 开发环境:Android 13 MTK平台 涉及修改的文件如下 device/mediatek/sepolicy/base/private/service_contexts device/mediatek/sepolicy/base/vendor/platfo…...

前端食堂技术周刊第 95 期:Fresh 1.4、Rollup 迁移至 SWC计划、RSC Devtools、使用开源库的边界、AI 帮你讲论文
美味值:🌟🌟🌟🌟🌟 口味:冰葡美式 食堂技术周刊仓库地址:https://github.com/Geekhyt/weekly 大家好,我是童欧巴。欢迎来到前端食堂技术周刊,我们先来看下…...

【TypeScript】枚举类型
在 TypeScript 中,枚举(Enum)是一种用于定义命名常量集合的数据类型。枚举使代码更加可读和可维护,因为它们为一组具有语义的值提供了命名。 以下是 TypeScript 中枚举的基本用法和特点: // 声明一个枚举 enum Direc…...
快速通过华为HCIP认证
你可以按照以下步骤进行准备和学习: 华为认证课程和资料--提取码:1234https://pan.baidu.com/s/1YJhD8QbocHhZ30MvrKm8hg 了解认证要求:查看华为官方网站上的HCIP认证要求和考试大纲,了解考试的内容、考试形式和考试要求。 学习相关知识&am…...

派森 #P124. 公式计算
描述 输入数正整数m,输出0! 1! ...m!的计算结果。 样例 输入 5 输出 154 代码: m int(input()) result 1 factorial 1 for i in range(1, m 1):factorial * iresult factorial print(result) # 法2def factorial(n):"""计…...

opencv进阶14-Harris角点检测-cv2.cornerHarris
类似于人的眼睛和大脑,OpenCV可以检测图像的主要特征并将这 些特征提取到所谓的图像描述符中。然后,可以将这些特征作为数据 库,支持基于图像的搜索。此外,我们可以使用关键点将图像拼接起 来,组成更大的图像。&#x…...
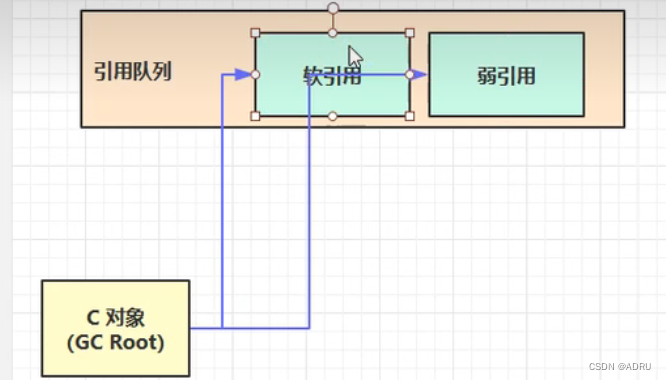
JVM中对象和GC Root之间的四种引用关系
1. 强引用 只有所有 GC Roots 对象都不通过【强引用】引用该对象,该对象才能被垃圾回收 由GC Root直接new出来的对象是强引用,只有当GC Root不再引用该对象的时候,才会被回收 例子: List<String> list new ArrayList<&…...
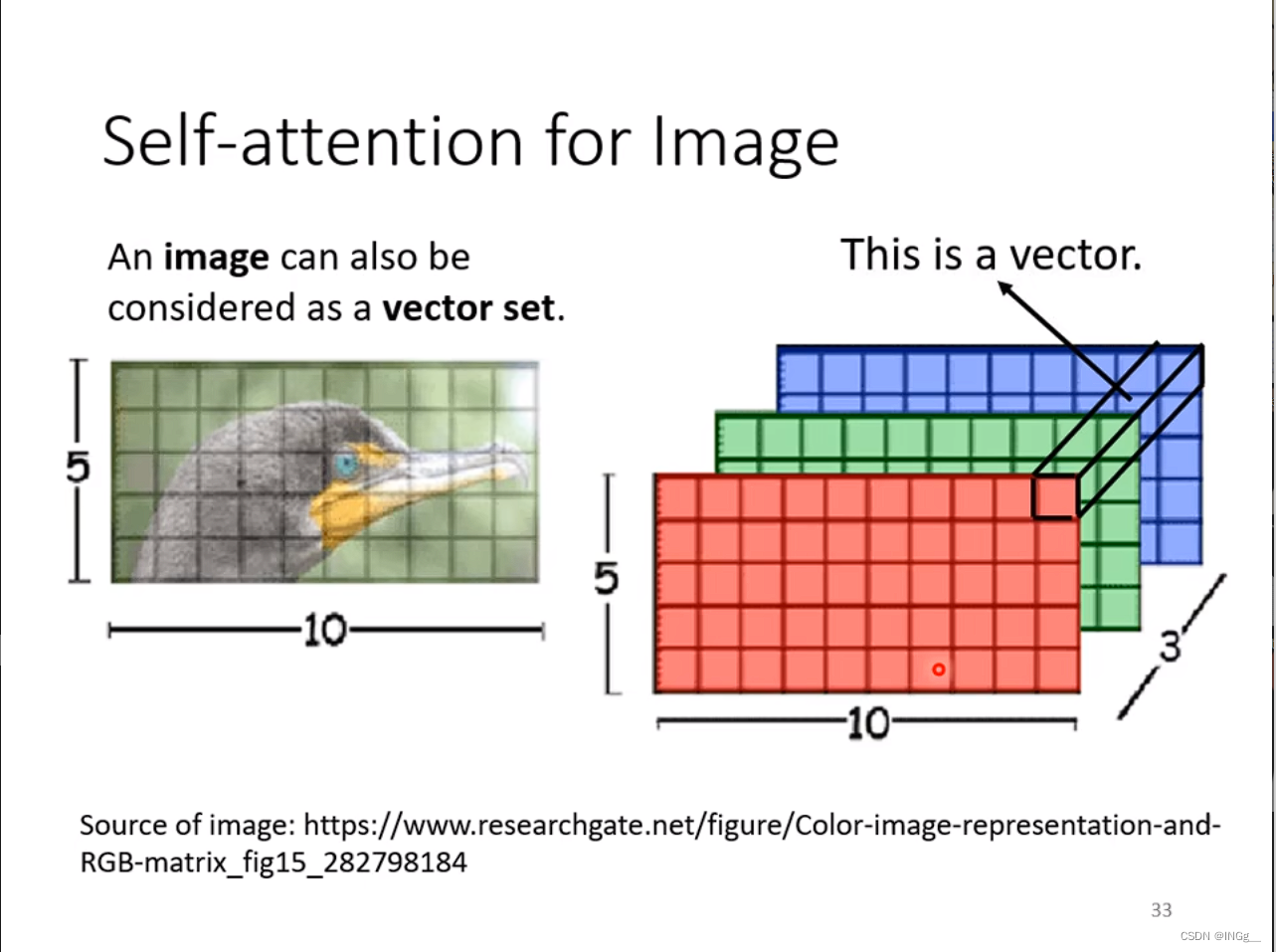
【李宏毅机器学习】注意力机制
输出 我们会遇到不同的任务,针对输出的不一样,我们对任务进行划分 给多少输出多少 给一堆向量,输出一个label,比如说情感分析 还有一种任务是由机器决定的要输出多少个label,seq2seq的任务就是这种,翻译也…...

Nginx使用keepalived配置VIP
VIP常用于负载均衡的高可用,使用VIP可以给多个主机绑定一个IP,这样,当某个负载应用挂了之后,可以自动切到另一个负载。 我这里是在k8s环境中做的测试,集群中有6个节点,我给140和141两个节点配置VIP。 1. 安…...
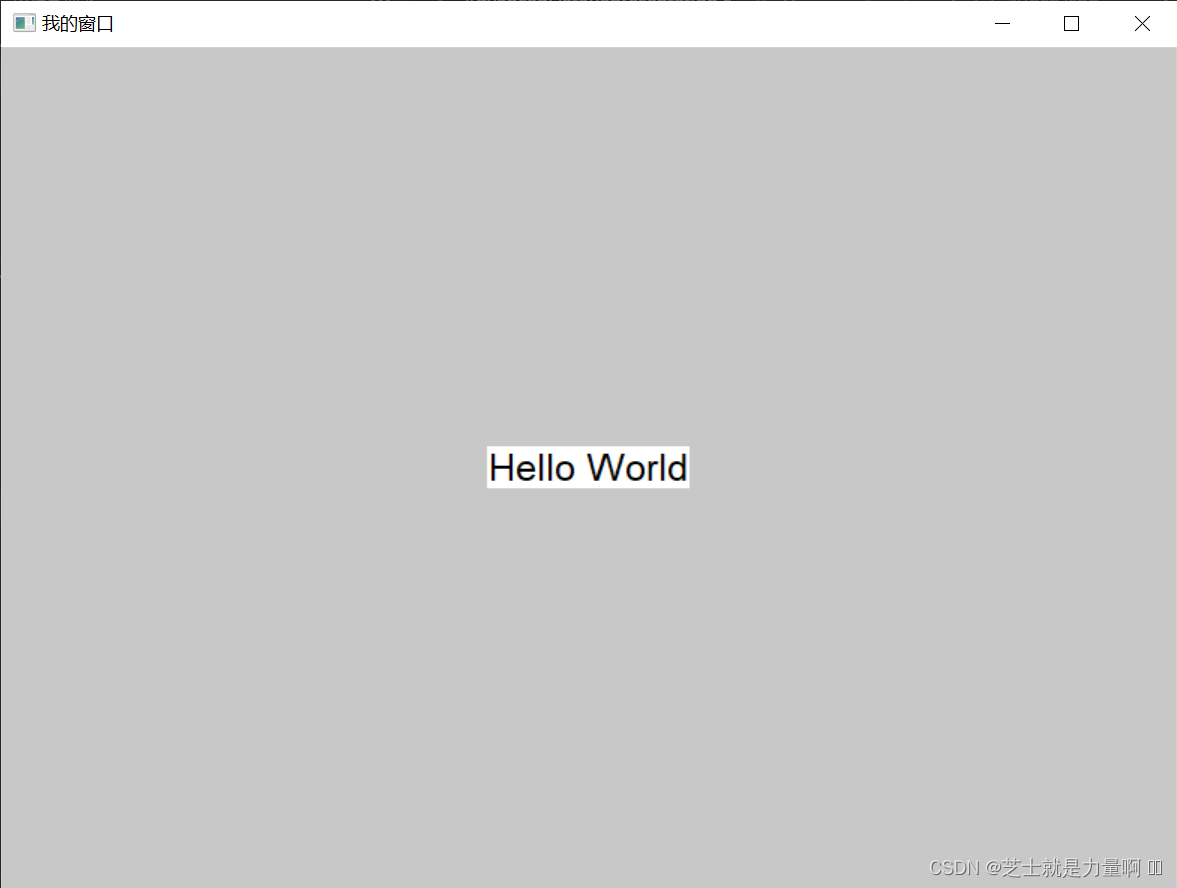
C语言编写图形界面
文章目录 环境使用库基础概念句柄 程序的入口创建窗口定义窗口类注册窗口类创建窗口 完整代码运行效果 环境 使用的是VSCode MinGW; 使用库 我们使用windows.h库来实现图形化界面。 头文件如下: #include <windows.h>windows.h是 Windows 操作…...
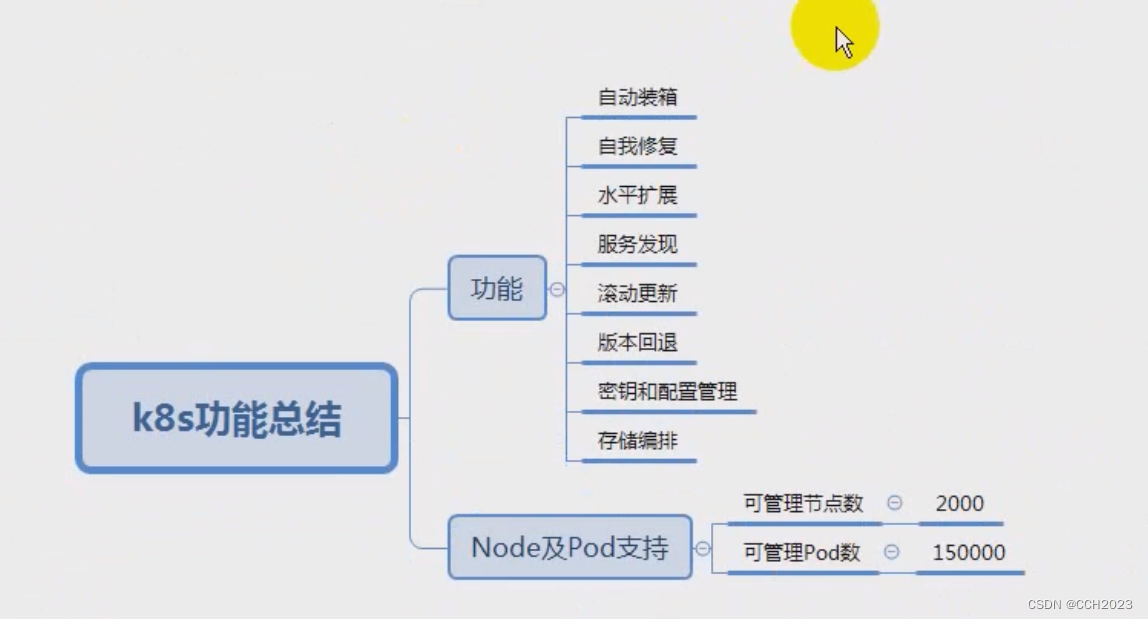
K8s学习笔记3
Kubernetes功能: Kubernetes是一个轻便的可扩展的开源平台,用于管理容器化应用和服务。通过Kubernetes能够进行应用的自动化部署和扩缩容。在Kubernetes中,会将组成应用的容器组合成一个逻辑单元以更易管理和发现。Kubernetes积累了作为Goog…...
ceph集群的扩容缩容
文章目录 集群扩容添加osd使用ceph-deploy工具手动添加 添加节点新节点前期准备新节点安装ceph,出现版本冲突 ceph-deploy增加节点 集群缩容删除osd删除节点 添加monitor节点删除monitor节点使用ceph-deploy卸载集群 实验所用虚拟机均为Centos 7.6系统,8…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...
