【数据结构入门指南】二叉树
【数据结构入门指南】二叉树
- 一、二叉树的概念
- 二、现实中的二叉树
- 三、特殊的二叉树
- 四、二叉树的性质
- 五、二叉树的存储结构
- 5.1 顺序结构
- 5.2 链式结构

一、二叉树的概念
二叉树是一棵特殊的树。一棵二叉树是结点的一个有限集合,该节点:
①:或者为空。
②: 由一个根节点加上两棵别称为左子树和右子树的二叉树组成。

从上图可以看出:
- 二叉树不存在度大于2的结点.
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树。
Tips:对于任意的二叉树都是由以下几种情况复合而成的:

二、现实中的二叉树

三、特殊的二叉树
① 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是2^k -1,则它就是满二叉树。
②完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。

四、二叉树的性质
①: 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2(i-1)个结点。
②: 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2h-1。
③: 对任何一棵二叉树, 如果度为0其叶结点个数为n0 , 度为2的分支结点个数为n2,则n0 = n2 +1。
④: 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h=log2(n+1)。
⑤:对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有:
- 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点。
- 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子。
- 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子。
五、二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
5.1 顺序结构
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费,/font.。而现实中使用中只有堆才会使用数组来存储。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。

5.2 链式结构
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。
通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链,到后期学到高阶数据结构如红黑树等会用到三叉链。


typedef int BTDataType;
// 二叉链
struct BinaryTreeNode
{struct BinTreeNode* _pLeft; // 指向当前节点左孩子struct BinTreeNode* _pRight; // 指向当前节点右孩子BTDataType _data; // 当前节点值域
}
// 三叉链
struct BinaryTreeNode
{struct BinTreeNode* _pParent; // 指向当前节点的双亲struct BinTreeNode* _pLeft; // 指向当前节点左孩子struct BinTreeNode* _pRight; // 指向当前节点右孩子BTDataType _data; // 当前节点值域
}


-【数据结构入门指南】二叉树顺序结构: 堆及实现(全程配图,非常经典)
相关文章:

【数据结构入门指南】二叉树
【数据结构入门指南】二叉树 一、二叉树的概念二、现实中的二叉树三、特殊的二叉树四、二叉树的性质五、二叉树的存储结构5.1 顺序结构5.2 链式结构 一、二叉树的概念 二叉树是一棵特殊的树。一棵二叉树是结点的一个有限集合,该节点: ①:或者…...

C++初阶——string(字符数组),跟C语言中的繁琐设计say goodbye
前言:在日常的程序设计中,我们会经常使用到字符串。比如一个人的身份证号,家庭住址等,只能用字符串表示。在C语言中,我们经常使用字符数组来存储字符串,但是某些场景(比如插入,删除)下操作起来很…...
之图片缓存详解)
Android Bitmap详解(下)之图片缓存详解
前言: 之前有出过俩篇关于bitmap相关的讲解,分别是Bitmap详解(上)常用概念和常用API和Bitmap详解(中)之像素级操作,今天主要是来一个系统的总结。 认识Bitmap: Bitmap是Android系统中的图像处理的最重要类之一。用它可以获取图像…...
)
020-从零搭建微服务-认证中心(九)
写在最前 如果这个项目让你有所收获,记得 Star 关注哦,这对我是非常不错的鼓励与支持。 源码地址(后端):https://gitee.com/csps/mingyue 源码地址(前端):https://gitee.com/csps…...

孤注一掷中的黑客技术
最近孤注一掷电影很火,诈骗团伙的骗术实在厉害,就连电影中的黑客潘生都未能幸免。电影中的陆经理说:不是我们坏, 是他们贪。这句话我觉得有一部分是对的,诈骗分子抓住了人的本性贪婪,才使得被骗的人逐步走向…...
)
机器学习笔记 - PyTorch Image Models图像模型概览 (timm)
一、简述 PyTorch Image Models (timm)是一个用于最先进的图像分类的库,包含图像模型、优化器、调度器、增强等的集合;是比较热门的论文及代码库。 虽然越来越多的低代码和无代码解决方案可以轻松开始将深度学习应用于计算机视觉问题,但我们经常与希望寻求定制解决方案的客户…...
Java 实现证件照底图替换,Java 实现照片头像底图替换
效果图 这里前端用layui实现的案例截图 color底图颜色可以在网页上这样取色 new Color(34, 133, 255) 实现案例下载链接:https://download.csdn.net/download/weixin_43992507/88237432...

周易卦爻解读笔记——未济
第六十四卦未济 火水未济 离上坎下 未济卦由否卦所变,否卦六二与九五换位,象征尚未完成。 天地否 未济卦和既济卦既是错卦又是覆卦,这也是最后一卦,序卦传【物不可穷也,故受之以未济终焉】 未济卦象征尚未完成&…...

AI 绘画Stable Diffusion 研究(十三)SD数字人制作工具SadTlaker使用教程
免责声明: 本案例所用安装包免费提供,无任何盈利目的。 大家好,我是风雨无阻。 想必大家经常看到,无论是在产品营销还是品牌推广时,很多人经常以数字人的方式来为自己创造财富。而市面上的数字人收费都比较昂贵,少则几…...

伦敦金走势图行情值得关注
不知道大家是否了解过伦敦金这个投资品种,或者有否财经网站以及金融终端上看到过它的行情走势图。其实,伦敦金并不是一种实实在在的黄金,而是一种跟踪伦敦现货黄金市场价格走势的黄金保证金交易品种,它每天的行情走势变化…...
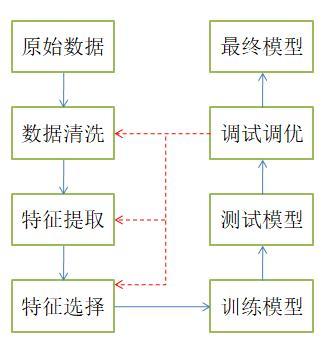
机器学习之数据清洗
一、介绍 数据清洗是机器学习中的一个重要步骤,它涉及对原始数据进行预处理和修复,以使数据适用于机器学习算法的训练和分析。数据清洗的目标是处理数据中的噪声、缺失值、异常值和不一致性等问题,以提高数据的质量和准确性。 二、方法 处理…...
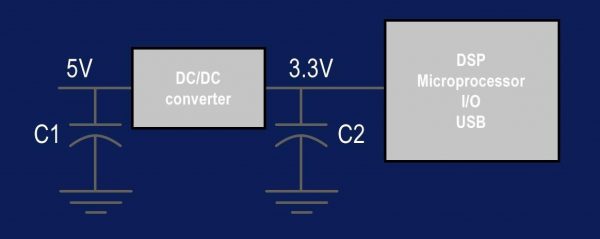
T599聚合物电容器:在汽车应用中提供更长的使用寿命的解决方案
自从电子技术被引入汽车工业以来,汽车的技术含量一直在提升。诸多技术被应用在汽车上,使汽车的形象更接近于轮子上的超级计算机。更多传感器、更强大的计算能力和电力被装载到汽车上,汽车应用中的电子产品数量正在迅速增长。随着电动汽车和自…...

学习ts(五)类
定义 是面向对象程序设计(OOP)实现信息封装的基础 类是一种用户定义的引用数据类型,也称类类型 JavaScript的class,虽然本质是构造函数,但是使用起来已经方便了许多,js中没有加入修饰符和抽象类等特性 ts的class支持面…...

EasyImage简单图床 - 快速搭建私人图床云盘同时远程访问【无公网IP内网穿透】
憧憬blog主页 在强者的眼中,没有最好,只有更好。我们是移动开发领域的优质创作者,同时也是阿里云专家博主。 ✨ 关注我们的主页,探索iOS开发的无限可能! 🔥我们与您分享最新的技术洞察和实战经验࿰…...
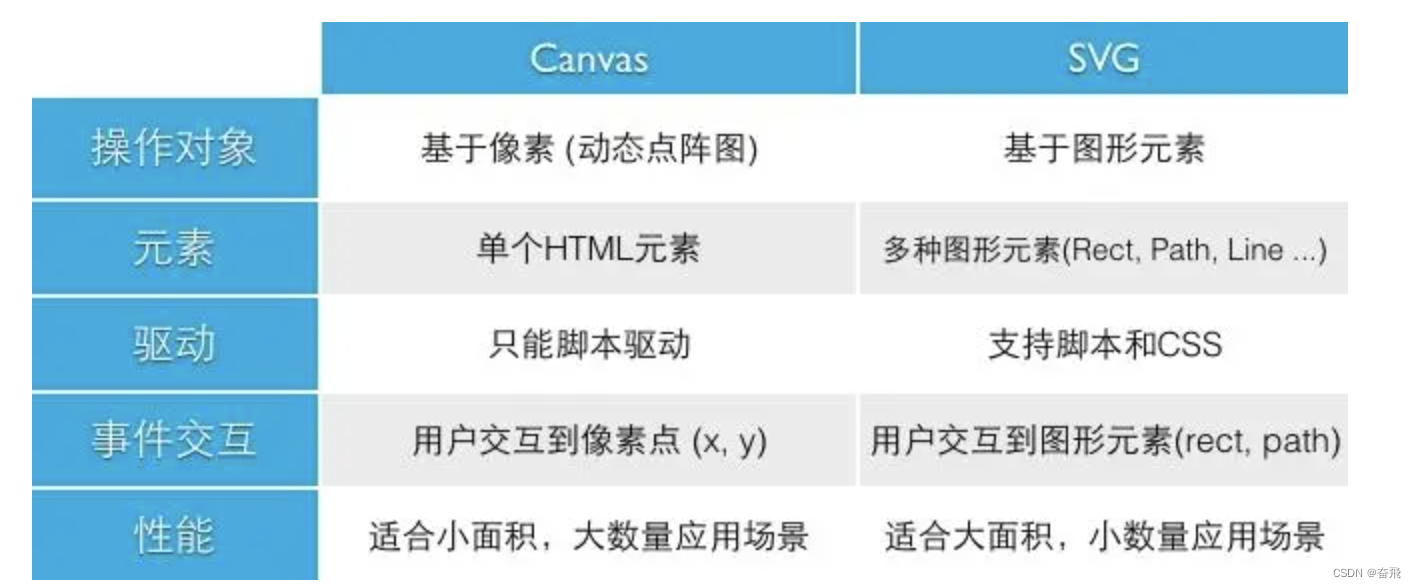
从SVG到Canvas:选择最适合你的Web图形技术
SVG 和 Canvas 都是可以在 Web 浏览器中绘制图形的技术。 众所周知, icon 通常使用 svg(如 iconfont),而交互式游戏采用 Canvas。二者具体的区别是什么?该如何选择? 声明式还是命令式?绘制的图形…...

基于 Redis 实现分布式限流
基于 Redis 实现分布式限流 一、 简介二、分布式限流1 数据结构1.1 Redis List1.2 Redis Set1.3 Redis Sorted Set 2 实现分布式限流3 实现原理分析 三、分布式限流算法1. 计数器算法2. 漏斗算法3. 令牌桶算法 四、分布式限流实战1. 单机限流实现2. 基于Redis Clusters的分布式…...

前端下载文件方式(Blob)
以下以下载图标svg文件为例,实现点击按钮下载文件,其中icon结构如下: const DownloadSvg (props) > {function download(downfile) {const tmpLink document.createElement("a");const objectUrl URL.createObjectURL(downfi…...
【STM32】FreeRTOS软件定时器学习
软件定时器 FreeRTOS提供了现成的软件定时器功能,可以一定程度上替代硬件定时器,但精度不高。 实验:创建一个任务,两个定时器,按键开启定时器,一个500ms打印一次,一个1000ms打印一次。 实现&…...
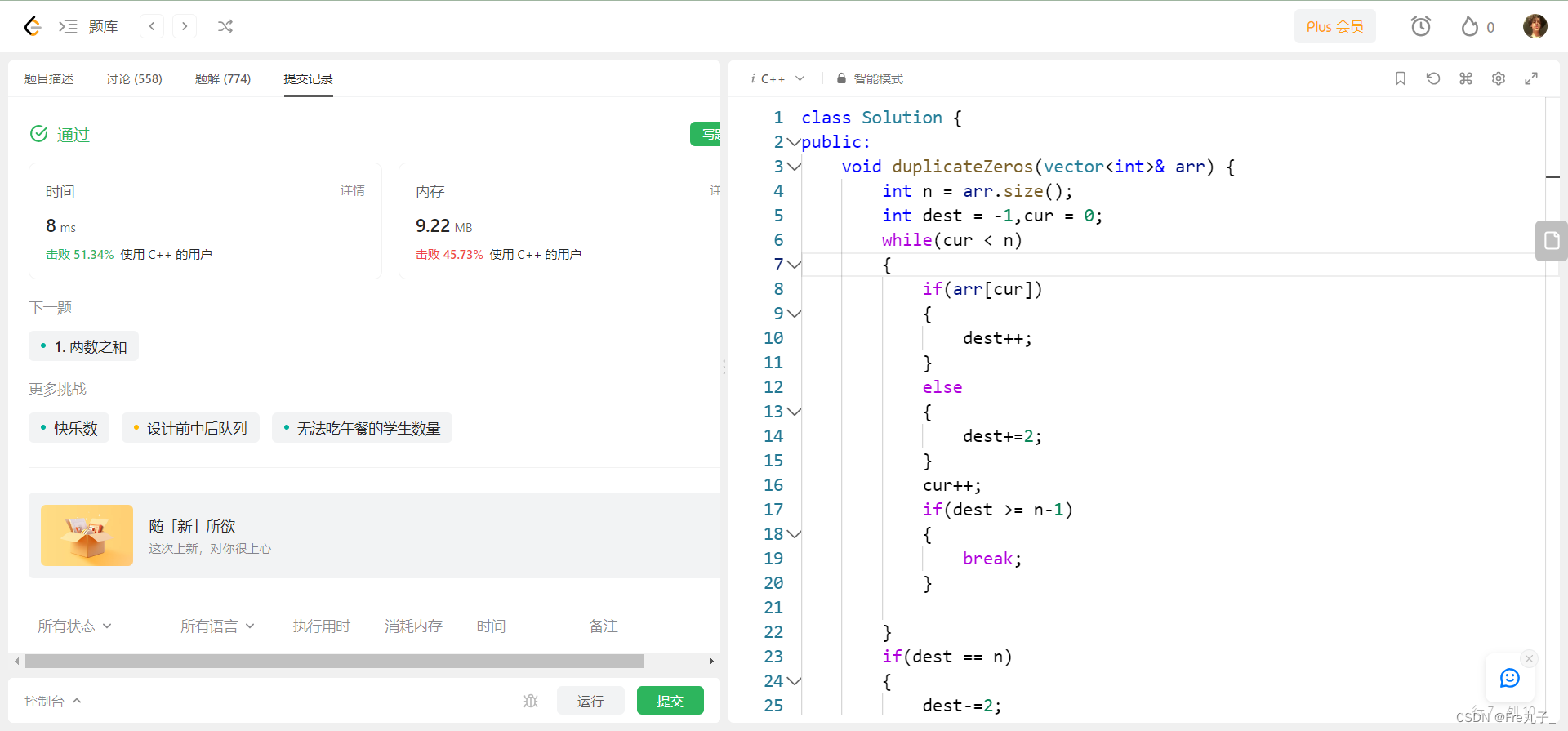
【LeetCode】复写零
复写零 题目描述算法描述编程代码 链接: 复写零 题目描述 算法描述 编程代码 class Solution { public:void duplicateZeros(vector<int>& arr) {int n arr.size();int dest -1,cur 0;while(cur < n){if(arr[cur]){dest;}else{dest2;}cur;if(dest > n-1){…...
使用docker-maven-plugin插件构建镜像并推送至私服Harbor
前言 如下所示,建议使用 Dockerfile Maven 插件,但该插件也停止维护更新了。因此先暂时使用docker-maven-plugin插件。 一、开启Docker服务器的远程访问 1.1 开启2375远程访问 默认的dokcer是不支持远程访问的,需要加点配置,开…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...
