当前位置：首页 > news >正文

数据结构-----树的易错点

news 文章来源：https://blog.csdn.net/weixin_69884785/article/details/132362530 2024/11/25 10:54:41

1.树的度和m叉树

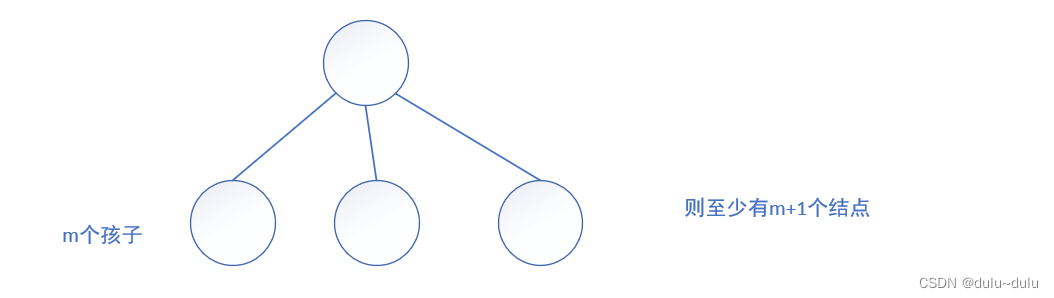
•度为m的树（度表示该结点有多少个孩子（分支））

任意结点的度<=m(最多m个孩子)

至少又一个结点度=m(有m个孩子)

一定是非空树，至少有m+1个结点

•m叉树

任意结点的度<=m(最多有m个孩子)

允许所有结点的度都<m

可以是空树

2.m叉树第i层至多有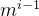 $m^{i-1}$ 个结点或度为m的树第i层至多有 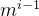$m^{i-1}$ 个结点

二叉树第i层至多有 $2^{i-1}$ 个结点

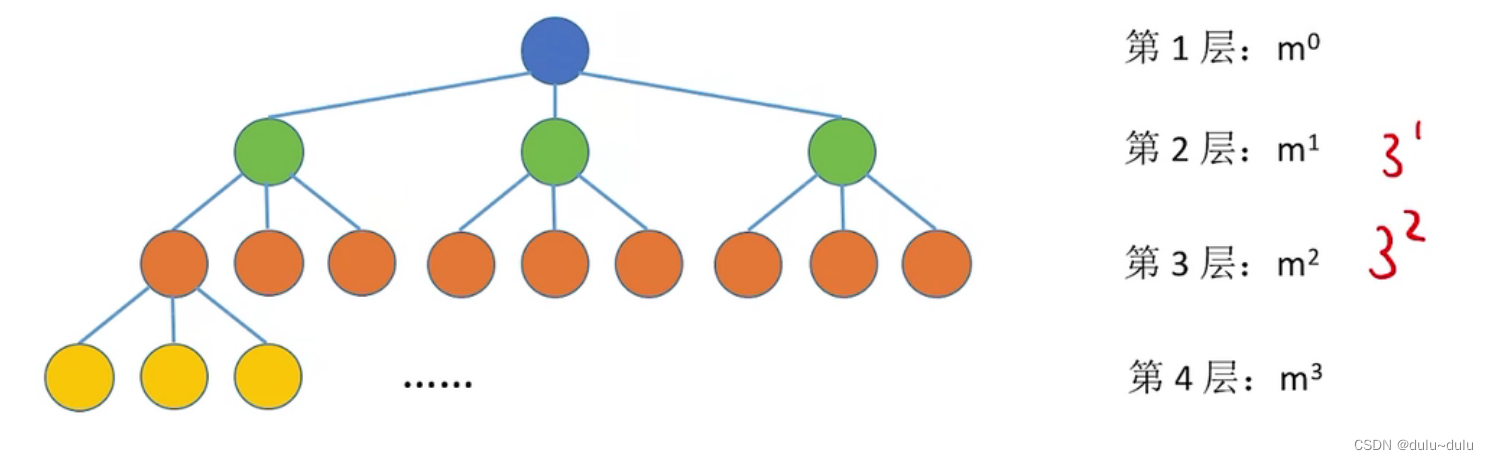
3.高度为h的m叉树至多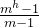 $\frac{m^{h}-1}{m-1}$ 个结点

高度为h的二叉树至多有 $2^{h}-1$ 个结点

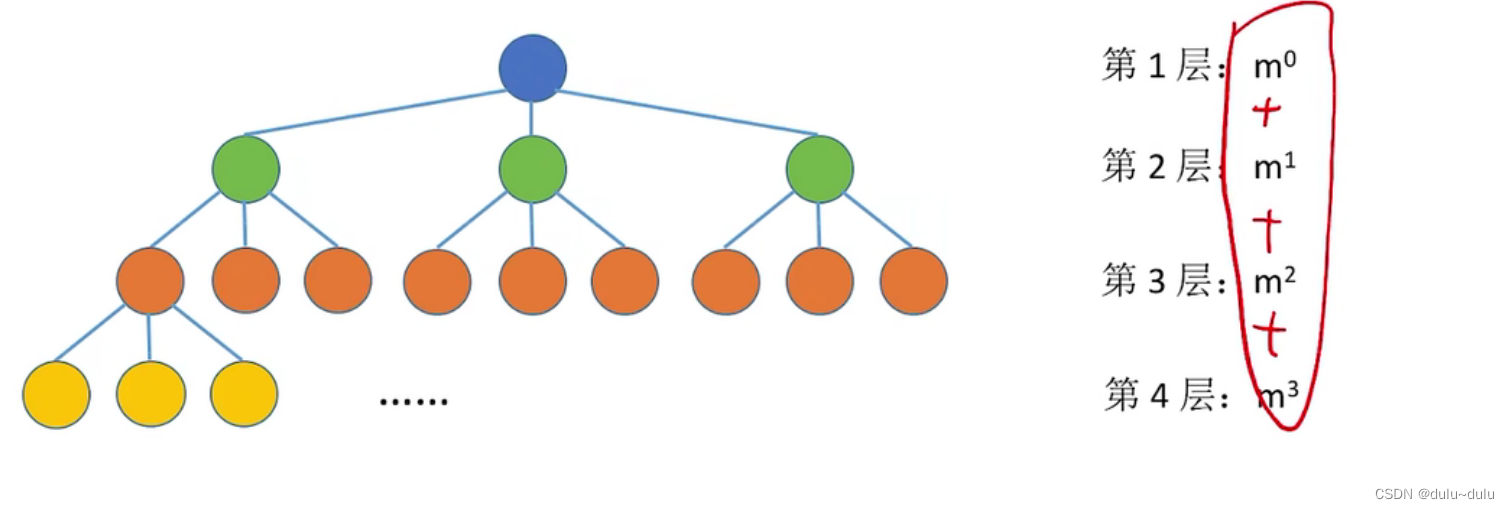
注：

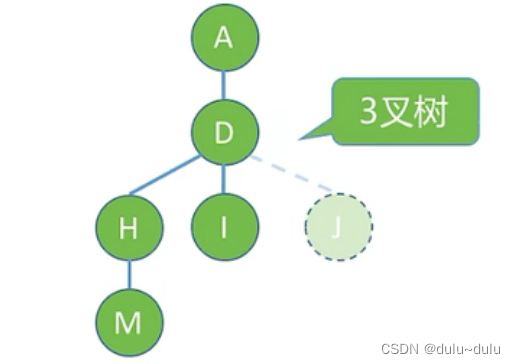
在这里，树的高度和深度可以看作相同的概念，因为这里侧重于树有几层，但是如果侧重于结点，那么高度和深度的概念就不同了

树的深度：(从上往下数)

节点 D、E 和 F 的深度都为 2，因为从根节点 A 到节点 D ，E，F需要经过 2 条边。

树的高度：(从下往上数)

节点 D、E 和 F 的高度都为 1，因为它们都到达任意叶子节点的路径长度最短，只需要经过 1 条边。

总的来说：

树的深度是指从根节点到某个节点的路径长度。
树的高度是指从某个节点到达任意叶子节点的最长路径长度。

4.高度为h的m叉树至少有h个结点（高度为h，度为m的树至少有h+m-1个结点）

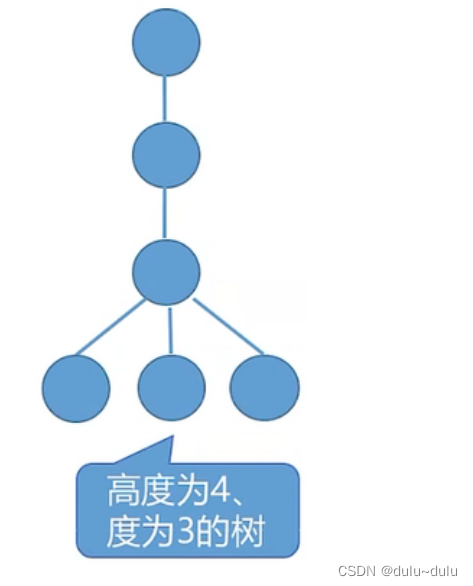
5.具有n个结点的m叉树的最小高度为 $\log _{m}^{(n(m-1)+1)}$

最小高度----每一个结点都有m个孩子

• $\frac{m^{h-1}-1}{m-1}$ $< n$ $\leq$ $\frac{m^{h}-1}{m-1}$

• $m^{h-1}<n(m-1)+1\leq m^{h}$

• $h-1<$ $\log _{m}^{(n(m-1)+1)}$ $\leq h$

• $h_{min}$ = $\log _{m}^{(n(m-1)+1)}$ (向上取整)

6.二叉树

(1).设非空二叉树中度为0，1，和2的结点个数分别为n0，n1，n2,则n0=n2+1（叶子节点的个数要比二分支节点的个数多一个）

假设结点总数为n

①n=n0+n1+n2

②n=n1+2n2+1(树的节点数=总度数+1)

(2).满二叉树

高度为h的二叉树，有 $2^{h}-1$ 个结点

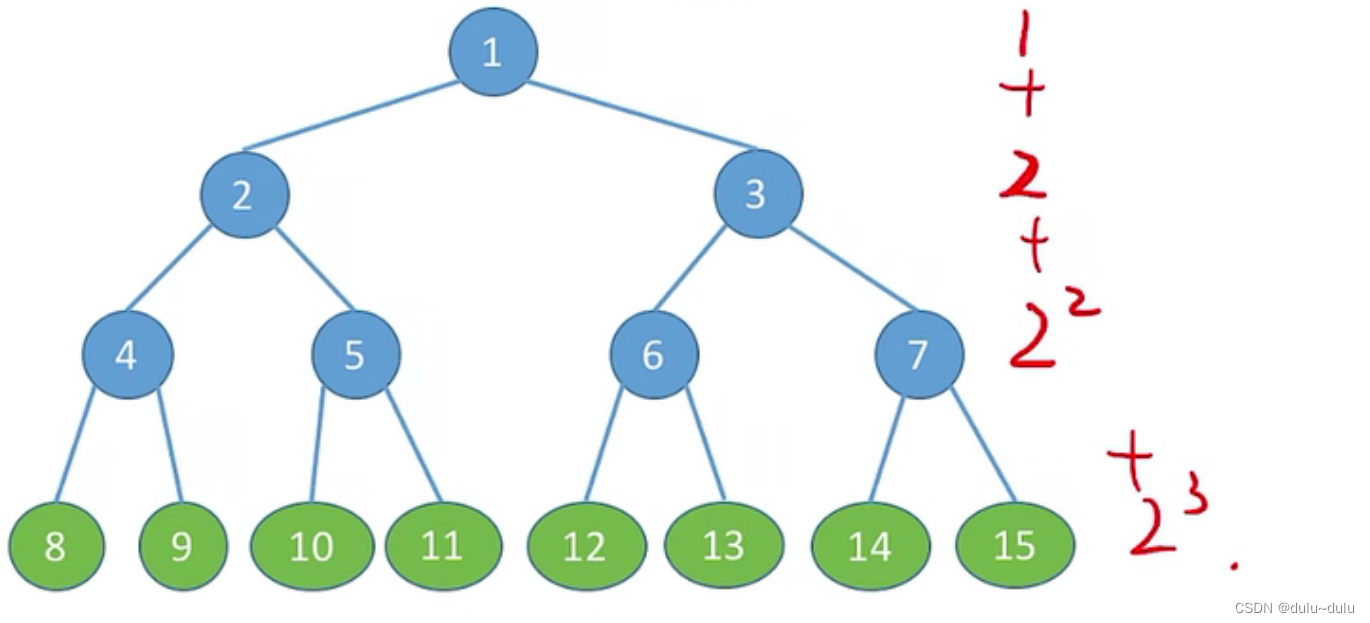
1.只有最后一层有叶子结点

2.不存在度为1的结点

3.按层序从1开始编号，结点i的左孩子为2i，右孩子为2i+1,结点i的父节点为i/2（向下取整）

6/2=3，7/2(向下取整)=3,所以6，7的父节点为3

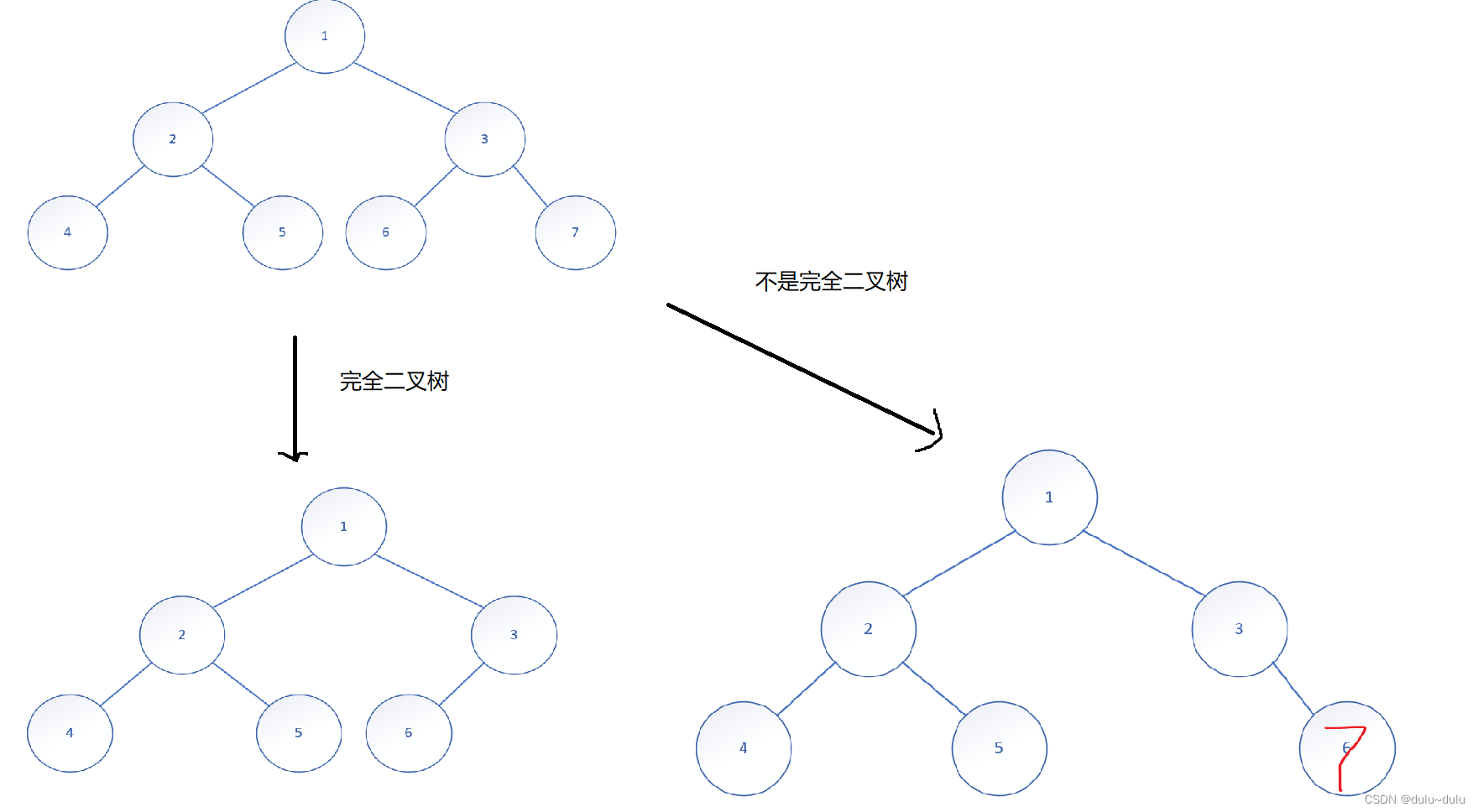
(3).完全二叉树

将叶子节点从大到小删去的，都可以称为完全二叉树，例如

右下角的图，6号结点在满二叉树中本来应该为7，所以序号变了，不是完全二叉树

得出结论

完全二叉树不一定是满二叉树，满二叉树一定是完全二叉树

①只有最后两层可以有叶子节点

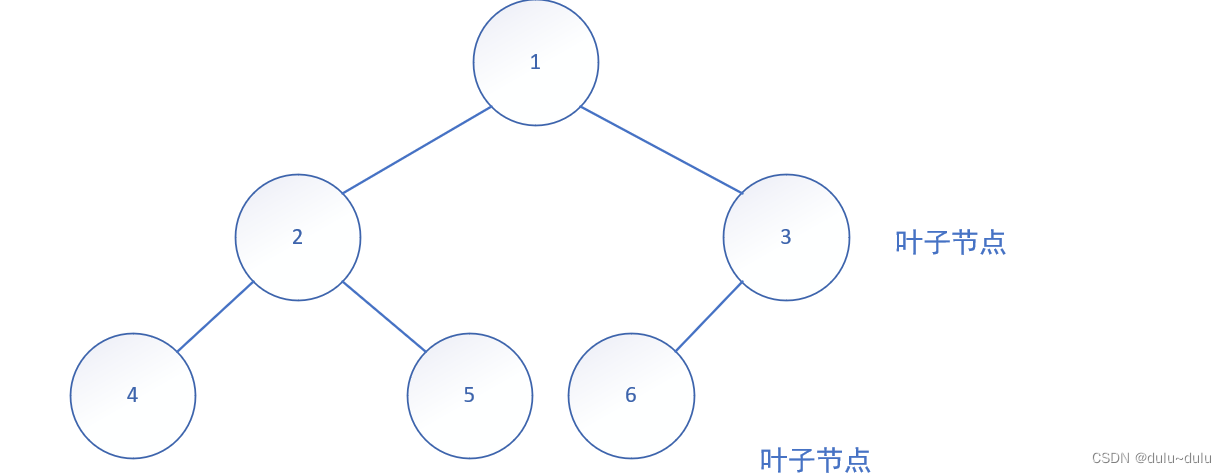
②最多只有1个度为1的结点

③按层序从1开始编号，结点i的左孩子为2i，右孩子为2i+1,结点i的父节点为i/2（向下取整）

④如果一个完全二叉树有n个结点，那么 $i\leq \frac{n}{2}$ (向下取整)为分支节点， $i\geq \frac{n}{2}$ (向下取整)为叶子节点

⑤如果某个节点只有1个结点，那么这个结点只可能是左孩子，不会是右孩子

⑥两个结论均正确

•具有n个（n>0）结点的完全二叉树的高度h（深度）为 $\log _{2}^{(n+1)}$ (向上取整)

推导过程

高为(h)的满二叉树共有 $2^{h}-1$ 个结点

高为(h-1)的满二叉树共有 $2^{h-1}-1$ 个结点

$2^{h-1}-1$ $<n\leqslant$ $2^{h}-1$

$2^{h-1}<n+1\leq 2^{h}$

$h-1<\log _{2}^{(n+1)}\leqslant h$

•具有n个（n>0）结点的完全二叉树的高度h（深度）为 $\log _{2}^{(n)}+1$ (向下取整)

高为h的完全二叉树至少 $2^{h-1}$ 个结点

高为h的完全二叉树至少 $2^{h}-1$ 个结点

$2^{h-1}\leqslant n \leqslant 2^{h}-1$

$2^{h-1}\leqslant n < 2^{h}$

$h-1\leqslant \log _{2}^{n}<h$

$h=$ $\log _{2}^{(n)}+1$ (向下取整)

⑦对于完全二叉树，可以优结点数n，推出度为0，1和2的结点个数为n0，n1和n2

完全二叉树最多只有一个度为1的结点，即

n1=0或1

n0=n2+1--->n0+n1一定为奇数

若完全二叉树有2k个结点，则必有n1=1，n0=k，n2=k-1

若完全二叉树有2k个结点，则必有n1=0，n0=k，n2=k-1

(4).二叉排序树

1.左子树上所有结点的关键字均小于根结点的关键字;

3.左子树和右子树又各是一棵二叉排序树。

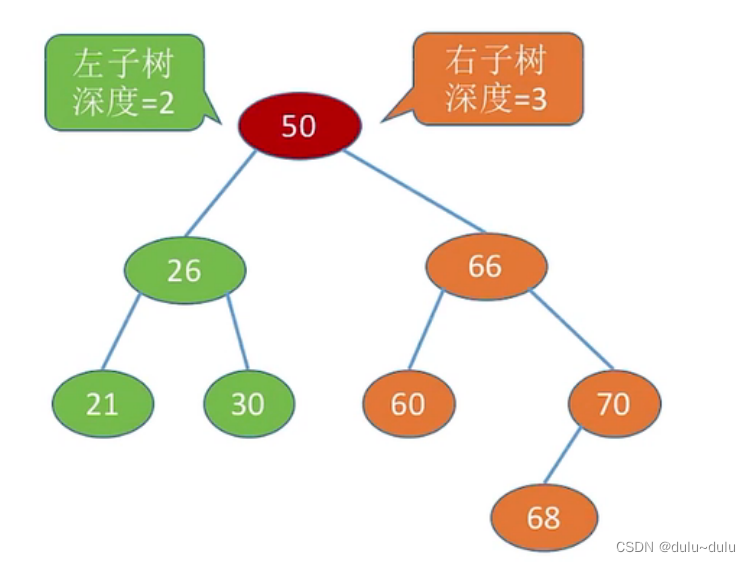
(5).平衡二叉树

树上任一结点的左子树和右子树深度(高度)之差不超过1

数据结构-----树的易错点

1.树的度和m叉树 •度为m的树（度表示该结点有多少个孩子（分支）） 任意结点的度<m(最多m个孩子) 至少又一个结点度m(有m个孩子) 一定是非空树，至少有m1个结点 •m叉树任意结点的度<m(最多有m个孩子) 允许所…...

编程日记 2023/8/23 7:46:49

写之前的项目关于使用git remote -v 找不到项目地址的解决方案

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档文章目录一、报错解析1. 报错内容2. 报错翻译3. 报错解析（1）使用git branch来查看git仓库有几个分支（2）使用git remote -v&am…...

编程日记 2023/8/23 7:45:47

STM32 F103C8T6学习笔记9：0.96寸单色OLED显示屏—自由取模显示—显示汉字与图片

今日学习0.96寸单色OLED显示屏的自由取模显示: 宋体汉字比较复杂，常用字符可以直接复制存下来，毕竟只有那么几十个字母字符，但汉字实在太多了，基本不会全部放在单片机里存着，一般用到多少个字就取几个字的模&#xff…...

编程日记 2023/8/23 7:44:45

直播平台源码搭建协议讲解篇：传输控制协议TCP

简介： 由于直播平台在当今时代发展的越来越迅速，使得直播平台的技术功能越来越智能，让用户在直播平台中能够和其他用户进行实时互动，让用户可以获取到全世界最新的资讯，让一些用户可以作为主播获得工作，让…...

编程日记 2023/8/23 7:43:44

中文编码问题：raw_input输入、文件读取、变量比较等str、unicode、utf-8转换问题

最近研究搜索引擎、知识图谱和Python爬虫比较多，中文乱码问题再次浮现于眼前。虽然市面上讲述中文编码问题的文章数不胜数，同时以前我也讲述过PHP处理数据库服务器中文乱码问题，但是此处还是准备简单做下笔记。方便以后查阅和大家学习。 …...

编程日记 2023/8/23 7:42:43

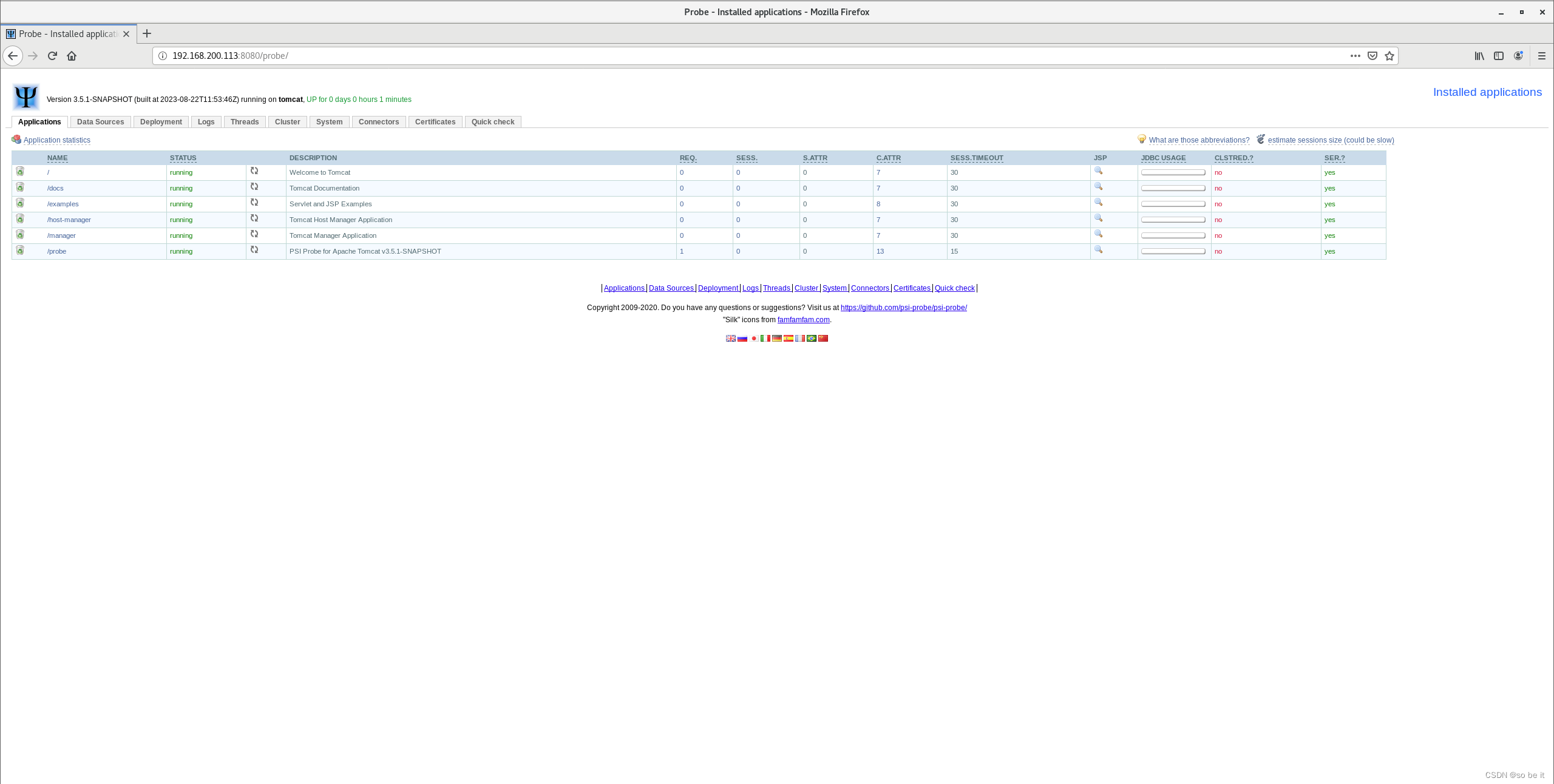
基于Jenkins自动打包并部署Tomcat环境

目录 1、配置git主机 2、配置jenkins主机 3、配置web主机 4、新建Maven项目 5、验证 Jenkins 自动打包部署结果 Jenkins 的工作原理是先将源代码从 SVN/Git 版本控制系统中拷贝一份到本地，然后根据设置的脚本调用Maven进行 build（构建）。…...

编程日记 2023/8/23 7:41:41

开利网络受邀参与御盛马术庄园发展专委会主题会议

近日，开利网络受邀参与深度合作客户御盛马术庄园组织的首届发展专委会主体会议，就马术庄园发展方向进行沟通，数字化也是重要议题之一。目前，御盛马术庄园已经完成数字化系统的初步搭建，将通过线上线下相结合的方式搭建…...

编程日记 2023/8/23 7:40:40

【HarmonyOS北向开发】-05 ArkTS开发语言-ArkTS开发实践

...

编程日记 2023/8/23 7:39:40

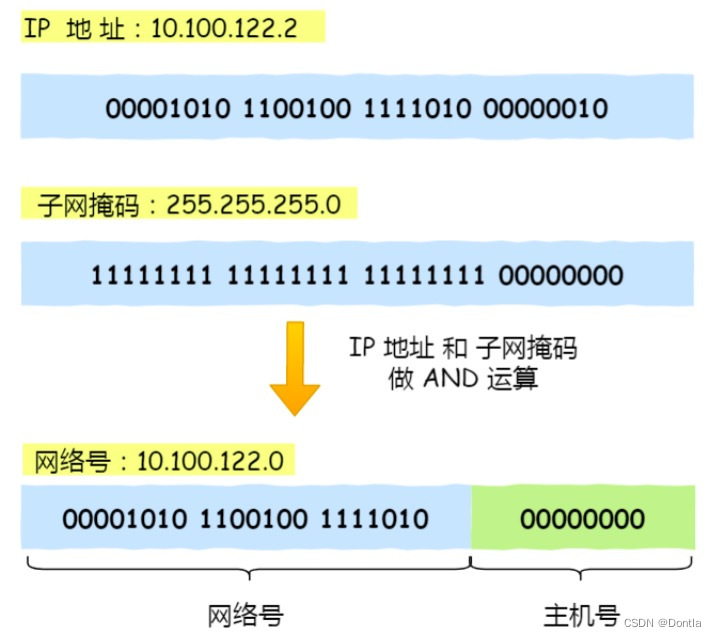
无类别域间路由（Classless Inter-Domain Routing, CIDR）：理解IP网络和子网划分（传统的IP地址类ABCDE：分类网络）

文章目录无类别域间路由（CIDR）：理解IP网络和子网划分引言传统的IP地址类关于“IP地址的浪费” IP地址与CIDRIP地址概述网络号与主机号CIDR记法（网络网络地址/子网掩码）网络和广播地址 CIDR的优势减少路由表项缓解IP…...

编程日记 2023/8/23 7:38:39

合宙Air724UG LuatOS-Air LVGL API-概念

概念在 LVGL 中，用户界面的基本构建块是对象。例如，按钮，标签，图像，列表，图表或文本区域。属性基本属性所有对象类型都共享一些基本属性： Position (位置) Size (尺寸) Parent (父母) Cli…...

编程日记 2023/8/23 7:37:37

【C语言】位段，枚举和联合体详解

目录 1.位段 1.1 什么是位段 1.2 位段的内存分配 1.3 位段的跨平台问题 2.枚举 2.1 枚举类型的定义 2.2 枚举的优点 3. 联合（共用体） 3.1 联合类型的定义 3.2 联合的特点 3.3 联合大小的计算 1.位段 1.1 什么是位段位段的声明和结构体是类…...

编程日记 2023/8/23 7:36:36

python学习-文件管理

文件管理 shutil 文件拷贝 shutil.copy(src,dst) 注：srcrE:\python\.vscode\文件操作 windows上运行时候，如果不加r，上述文件路径在代码运行时会报错，因为其会先将双引号”“去掉，然后系统看到了文件路径中有\nc&…...

编程日记 2023/8/23 7:35:34

【LeetCode 算法】Number of Ways of Cutting a Pizza 切披萨的方案数-记忆化

文章目录 Number of Ways of Cutting a Pizza 切披萨的方案数问题描述：分析代码递归 Tag Number of Ways of Cutting a Pizza 切披萨的方案数问题描述： 给你一个 rows x cols 大小的矩形披萨和一个整数 k ，矩形包含两种字符： A…...

编程日记 2023/8/23 7:34:32

机器视觉之光流

光流（Optical Flow）是计算机视觉领域的一个重要概念，用于描述图像中物体的运动模式。光流可以用来跟踪图像中物体的运动，检测运动中的物体，或者在机器视觉任务中估计物体的速度和位移。光流的基本思想是根据图像像素…...

编程日记 2023/8/23 7:33:31

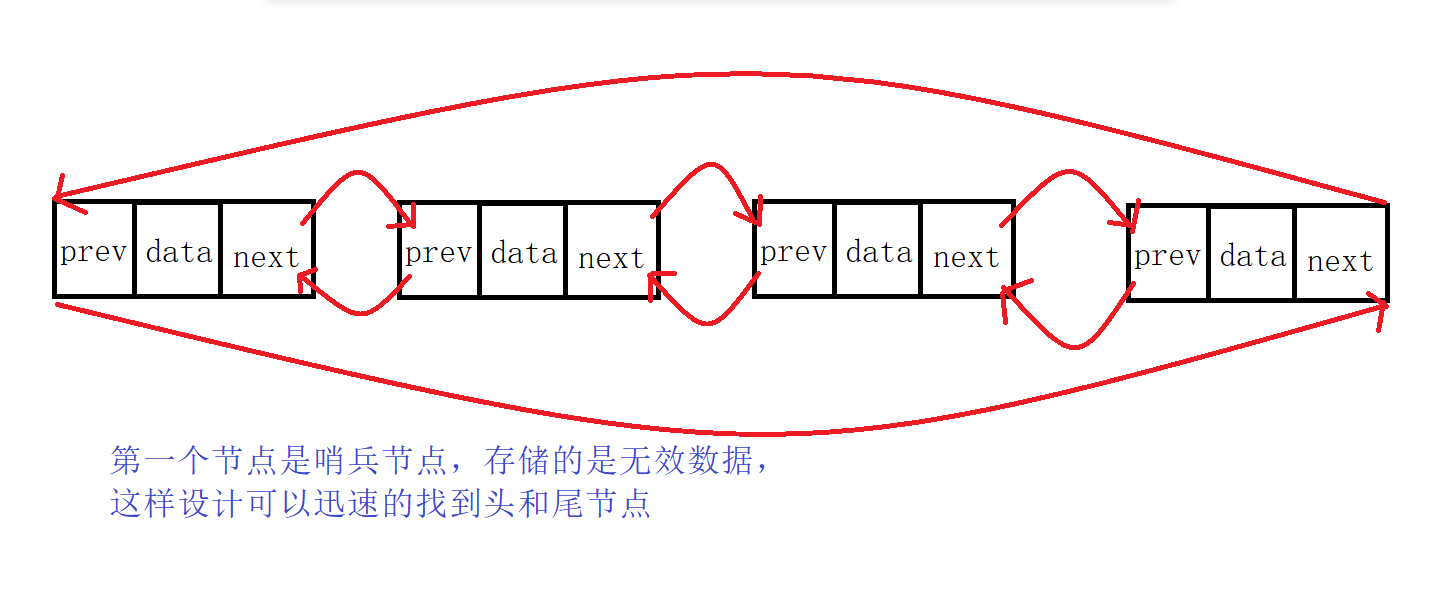
C++：list使用以及模拟实现

list使用以及模拟实现 list介绍list常用接口1.构造2.迭代器3.容量4.访问数据5.增删查改6.迭代器失效 list模拟实现1.迭代器的实现2.完整代码 list介绍 list是一个类模板，加<类型>实例化才是具体的类。list是可以在任意位置进行插入和删除的序列式容器。list的…...

编程日记 2023/8/23 7:32:29

深度学习基础知识-pytorch数据基本操作

1.深度学习基础知识 1.1 数据操作 1.1.1 数据结构机器学习和神经网络的主要数据结构，例如 0维：叫标量，代表一个类别，如1.0 1维：代表一个特征向量。如 [1.0，2,7，3.4] 2维：就是矩…...

编程日记 2023/8/23 7:31:27

Springboot使用QueryDsl实现融合数据查询

SpringbootQueryDsl技术 1、添加依赖  <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-jpa</artifactId> </dependency>  <dependenc…...

编程日记 2023/8/23 7:30:26

解决方案 | 电子签打通消费电子行业数智化经营通路

技术迭代不断驱动产业快速增长，从PC电脑到手机平板、再到可穿戴设备的兴起，每一次设备的迭代都代表着技术为产品注入了新的发展动能。与此同时，消费电子设备迭代更新周期的不断缩短，市场增长疲缓等因素，也对行业的流转…...

编程日记 2023/8/23 7:29:25

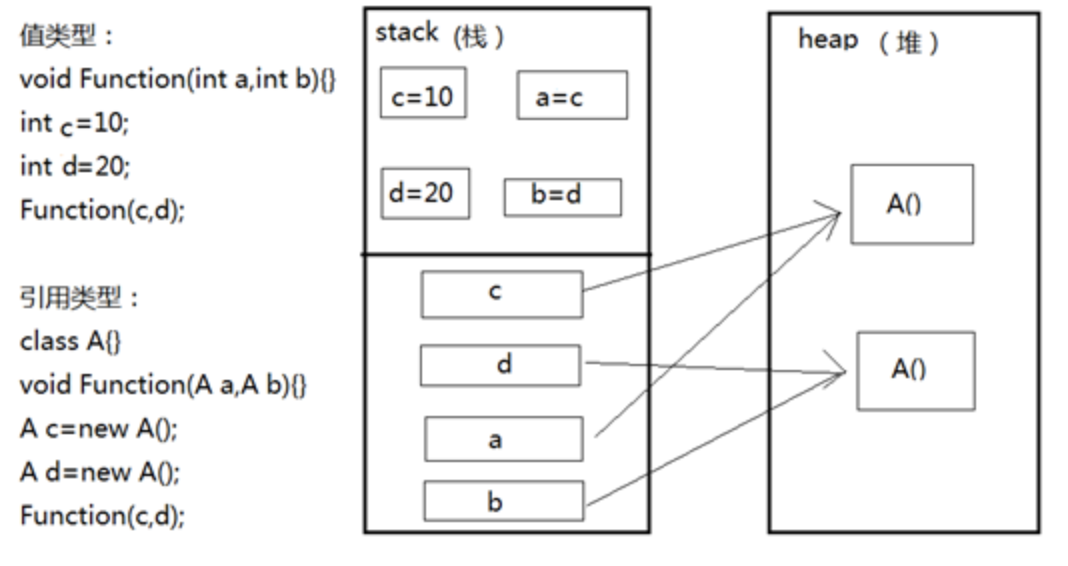
JVM理论知识

一、JVM内存结构 java的内存模型主要分为5个部分，分别是：JVM堆、JVM栈、本地栈、方法区还有程序计数器，他们的用途分别是： JVM堆：新建的对象都会放在这里，他是JVM中所占内存最大的区域。他又分为新生区还…...

编程日记 2023/8/23 7:28:22

idea - 报错 Mybatis提示Tag name expected的问题＜小于号无法识别

问题：Mybatis提示Tag name expected 原因： 当我们在mapper中编写sql语句的时候会发现使用"<“符号会提示一个Tag name expected。这是因为xml文件中不识别”<"符号和“&”符号。防止与xml本身的元素命名混淆，导致无法解…...

编程日记 2023/8/23 7:27:21

合宙Air724UG LuatOS-Air LVGL API--对象

对象概念在 LVGL 中，用户界面的基本构建块是对象。例如，按钮，标签，图像，列表，图表或文本区域。属性基本属性所有对象类型都共享一些基本属性： Position (位置) Size (尺寸) Parent (父母…...

编程日记 2023/8/23 7:26:18

Java将PDF文件转为Word文档

Java将PDF文件转为Word文档一、创建Springboot Maven项目二、导入依赖信息 <repositories><repository><id>com.e-iceblue</id><url>https://repo.e-iceblue.cn/repository/maven-public/</url></repository></repositories&g…...

编程日记 2023/8/23 7:25:17

vite创建项目命令

1.第一步运行创建命令（npm） npm create vitelatest也可以使用yarn yarn create vite还可以 pnpm create vite注意的地方：首次创建的时候会出现这个 Need to install the following packages:create-vitelatest Ok to proceed? (y) 直接y就…...

编程日记 2023/8/23 7:24:15

解决Pandas KeyError: “None of [Index([...])] are in the [columns]“问题

🌷🍁 博主猫头虎带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》文章图文并茂🦕生动形象🦖简单易学！欢迎大家来踩踩~🌺 &a…...

编程日记 2023/8/23 7:23:14

前端加springboot实现Web Socket连接通讯以及测试流程（包括后端实现心跳检测）

【2023】前端加springboot实现Web Socket连接通讯（包括后端实现心跳检测） 一级目录二级目录三级目录前言一、Web Socket 简绍1 为什么用 websocket？ 二、代码实现1、前端（html）1.1、无前端向后端发送消息1.2、有前端向…...

编程日记 2023/8/23 7:22:13

node使用高版本的oracledb导致连接oracle的Error: NJS-138异常

异常信息如下 Error: NJS-138: connections to this database server version are not supported by node-oracledb in Thin mode 我的oracle版本是11g，之前的使用正常，今天却报错了，显示不支持thin模式，后面回退版本就可以了。...

编程日记 2023/8/23 7:21:12

RabbitMQ手动签收消息

RabbitMQ手动签收消息这里讲解SpringBoot使用RabbitMQ进行有回调的用法和消费者端手动签收消息的用法。 1、pom依赖 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"h…...

编程日记 2023/8/23 7:20:08

不考虑性能很简陋的一个功能，主要是用于角色渲染的观察用，比simplecontroller要好用一点 using System; using UnityEngine;public class CharacterViewer : MonoBehaviour {public Transform target; // 人物模型的Transformpublic float rotationSpee…...

编程日记 2023/8/23 7:19:07

Spring Boot 将 Word 转换为 PDF

首先，确保项目中添加了对Apache POI和Apache PDFBox的依赖。可以在你的 pom.xml 文件中添加以下依赖： <dependencies><dependency><groupId>org.apache.poi</groupId><artifactId>poi</arti…...

编程日记 2023/8/23 7:18:05

【PHP面试题82】system和exec是用来做什么的？有什么区别

文章目录 🚀一、前言，PHP中system和exec命令的作用🚀二、system()函数🚀三、exec()函数🚀四、区别和应用场景🔎4.1 使用system()函数的应用场景🔎4.2 使用exec()函数的应用场景🔎4.3…...

编程日记 2023/8/23 7:17:04

网站主体证件/免费b2b平台推广

《PHP实例：php中getservbyport与getservbyname函数用法实例》要点：本文介绍了PHP实例：php中getservbyport与getservbyname函数用法实例，希望对您有用。如果有疑问，可以联系我们。代码如下:string getservbyport ( int …...

编程日记 2024/11/25 9:37:26

给传销做网站/网络营销的好处和优势

在 Android 所有的控件和 Layout 都有着一个父类 View 。Anroid 通过继承的方式，对父类控件进行继承，由此来在父类基础上创造新的控件。View我们先看看 View 这个父类Paste_Image.png可以看到间接继承的有100多个子类，不得不说 View 这个爹很…...

编程日记 2024/11/25 7:24:45

做名片赞机器人电脑网站是多少钱/关键词的作用

1、运行 npm i sass-loader node-sass -D 2、配置webpack.config.js文件 const path require(path);const HtmlWebpackPlugin require(html-webpack-plugin); //创建插件的实例对象 const htmlPlugin new HtmlWebpackPlugin({//指定要用到的模板template:./src/index.htm…...

编程日记 2024/11/25 6:59:22