概率论与数理统计:第七章:参数估计 第八章:假设检验
文章目录
- Ch7. 参数估计
- 7.1 点估计
- 1.矩估计
- 2.最大似然估计
- (1)离散型
- (2)连续型
- 7.2 评价估计量优良性的标准
- (1)无偏性 (无偏估计)
- (2)有效性
- (3)一致性
- 7.3 区间估计
- 1.置信区间、置信度
- 2.求μ的置信区间
- Ch8. 假设检验
- 1.拒绝域α、接受域1-α、H₀原假设、H₁备择假设
- 2.双边检验、单边检验
- 3.第一类错误、第二类错误
Ch7. 参数估计
7.1 点估计
1.矩估计
p i ( θ ) p_i(θ) pi(θ)、 f ( x i , θ ) f(x_i,θ) f(xi,θ),用矩估计法来估计未知参数θ
{ X ˉ = E ( X ) 1 n ∑ i = 1 n X i 2 = E ( X 2 ) \left\{\begin{aligned} \bar{X} = & E(X) \\ \dfrac{1}{n}\sum\limits_{i=1}^nX_i^2 = & E(X^2) \end{aligned}\right. ⎩ ⎨ ⎧Xˉ=n1i=1∑nXi2=E(X)E(X2)
注意:
1.矩估计量:大写
矩估计值:小写
2.离散型和连续型随机变量
求矩估计的区别,只在于求期望的方法不一样。
而求最大似然估计,则是似然函数的求法不一样。
例题1:23李林六套卷(三)22.(2)
若θ为未知参数,利用总体Z的样本值 − 2 , 0 , 0 , 0 , 2 , 2 -2,0,0,0,2,2 −2,0,0,0,2,2求 θ θ θ的矩估计值。且Z的分布律为
| Z Z Z | − 2 -2 −2 | 0 0 0 | 2 2 2 |
|---|---|---|---|
| P k P_k Pk | θ θ θ | 1 − 2 θ 1-2θ 1−2θ | θ θ θ |
答案:

例题2:09年23(1)

分析:
①矩估计,求期望
②最大似然估计,求似然函数L(θ),取对数lnL(θ),令导数为0即令 d l n L ( θ ) d θ = 0 \frac{\rm dlnL(θ)}{\rm dθ}=0 dθdlnL(θ)=0
答案:
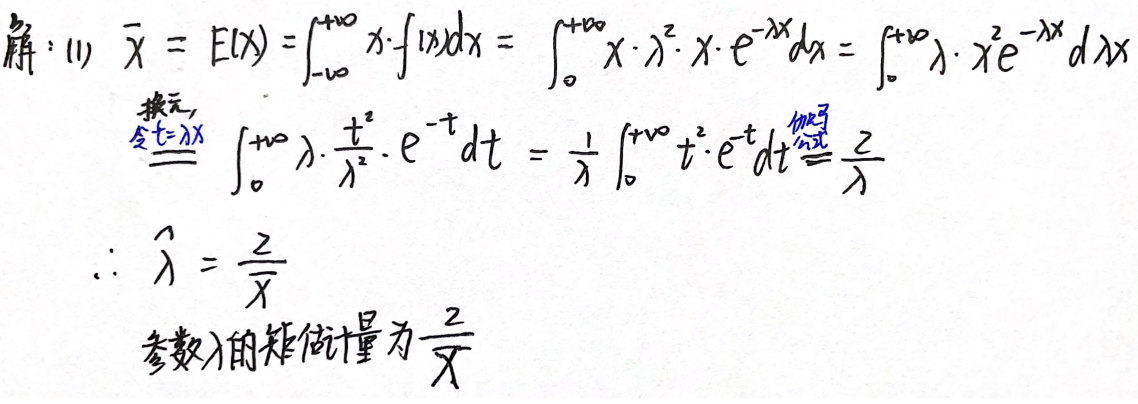
例题3:13年23.(难度:易)

2.最大似然估计
最大似然估计求的是,θ为多少时,使得L(θ)最大
(1)离散型
求离散型随机变量的最大似然估计量:
离散型的似然函数 L ( θ ) = ∏ i = 1 n p ( x i , θ ) L(θ)=\prod\limits_{i=1}^n{p(x_i,θ)} L(θ)=i=1∏np(xi,θ) = p ( x 1 , θ ) ⋅ p ( x 2 , θ ) ⋅ . . . ⋅ p ( x n , θ ) =p(x_1,θ)·p(x_2,θ)·...·p(x_n,θ) =p(x1,θ)⋅p(x2,θ)⋅...⋅p(xn,θ)
x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn为离散型样本值,根据样本来确定是哪些概率相乘。
(2)连续型
求连续型随机变量的最大似然估计量,连续型的似然函数L(θ)
L ( θ ) = L ( x 1 , x 2 , . . . , x n ; θ ) = ∏ i = 1 n f ( x i ; θ ) ( x i > 0 , i = 1 , 2 , . . . n ) L(θ) = L(x_1,x_2,...,x_n;θ) = \prod_{i=1}^n f(x_i;θ) \qquad (x_i>0,i=1,2,...n) L(θ)=L(x1,x2,...,xn;θ)=i=1∏nf(xi;θ)(xi>0,i=1,2,...n)
求最大似然估计量/值
①求似然函数 L(θ) (xi>0/θ,i=1,2,…n)
②取对数,求 lnL(θ)
③令 d l n L ( θ ) d θ = 0 \frac{\rm d lnL(θ)}{\rm dθ} = 0 dθdlnL(θ)=0,求出 θ ^ \hat{θ} θ^
④最大似然估计值为xi,最大似然估计量为Xi
若 d l n L ( θ ) d θ ≠ 0 \frac{\rm d lnL(θ)}{\rm dθ} ≠ 0 dθdlnL(θ)=0
有的题,在③这一步发现 d l n L ( θ ) d θ ≠ 0 \frac{\rm d lnL(θ)}{\rm dθ} ≠ 0 dθdlnL(θ)=0,为>0就说明 L(θ)为增函数。见2000年21.
例题1:2002年20. 离散型的参数估计
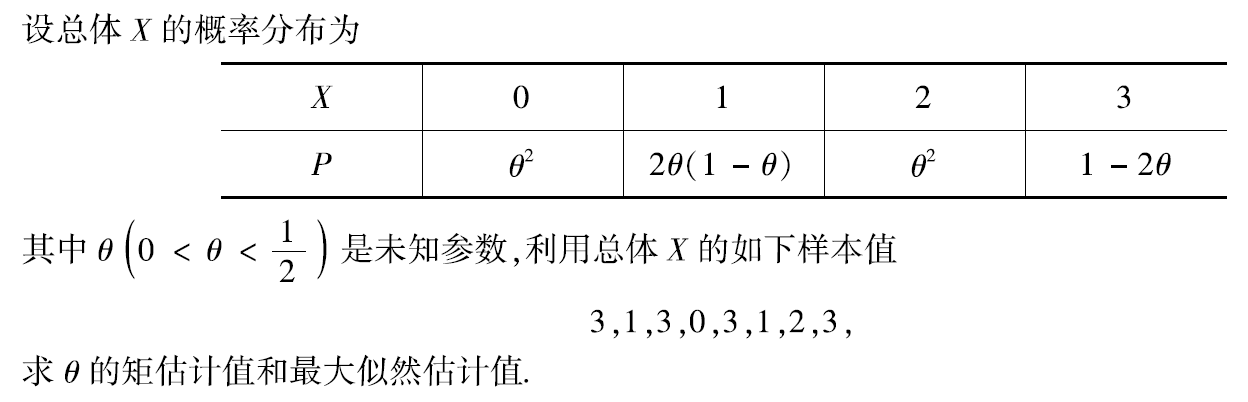
答案:

例题2:19年23(2)

分析:
求σ2的最大似然函数:
①求似然函数L(σ2)
②取对数,lnL(σ2)
③令 d l n L ( σ 2 ) d σ 2 = 0 \frac{\rm d lnL(σ^2)}{\rm dσ^2} = 0 dσ2dlnL(σ2)=0
答案:
σ2的最大似然估计值为 σ ^ 2 = 1 n ∑ i = 1 n ( x i − μ ) 2 \hat{σ}^2=\dfrac{1}{n}\sum\limits_{i=1}^n(x_i-μ)^2 σ^2=n1i=1∑n(xi−μ)2
σ2的最大似然估计量为 σ ^ 2 = 1 n ∑ i = 1 n ( X i − μ ) 2 \hat{σ}^2=\dfrac{1}{n}\sum\limits_{i=1}^n(X_i-μ)^2 σ^2=n1i=1∑n(Xi−μ)2
例题3:18年23(2)
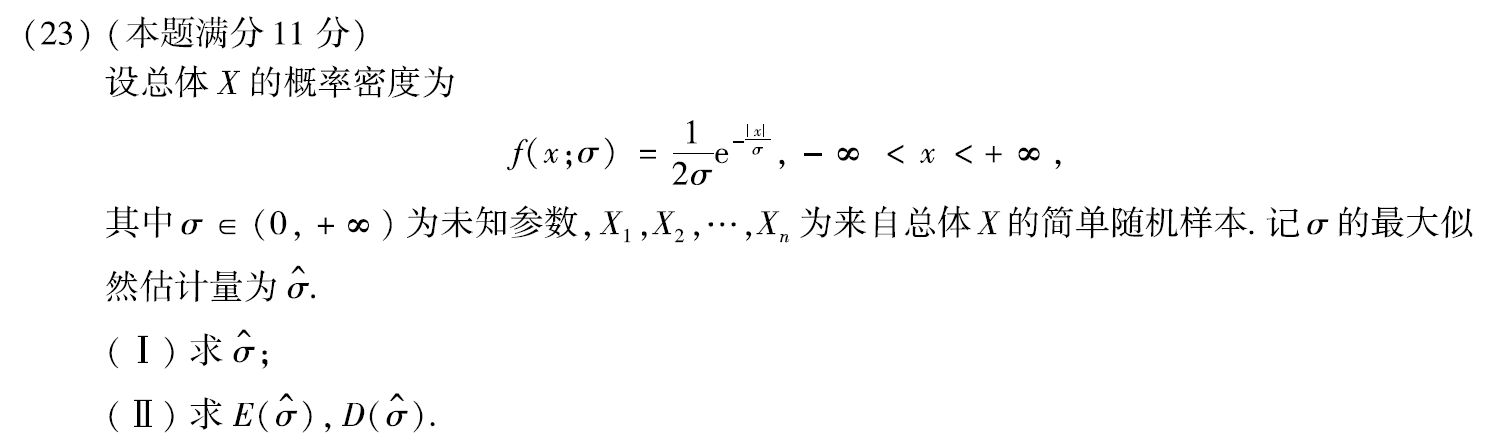
例题4:2000年21.
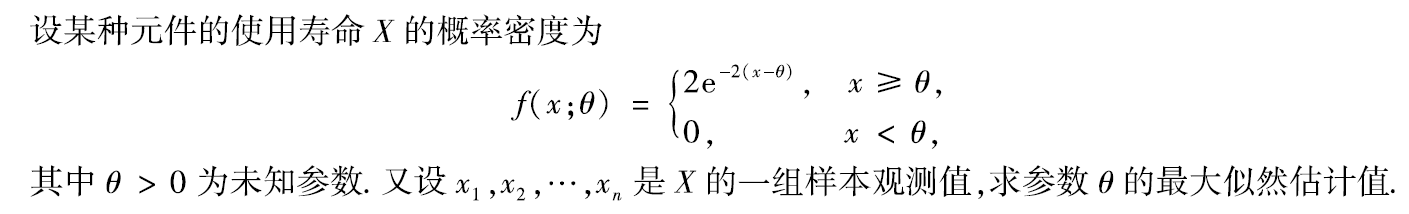
分析: d l n L ( θ ) d θ = 2 n > 0 \frac{\rm d lnL(θ)}{\rm dθ} =2n >0 dθdlnL(θ)=2n>0,∴lnL(θ)为关于θ的增函数
∴θ的最大似然估计值为 θ ^ \hat{θ} θ^=min1≤i≤n{xi}
例题5:09年23(2)
习题1:23李林四(三)16.
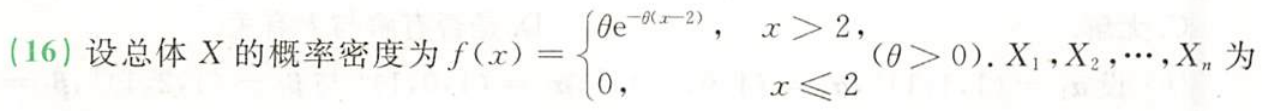
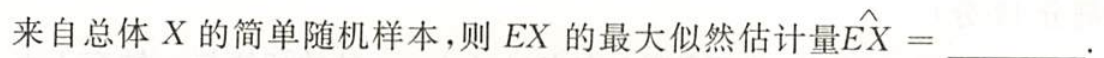
分析:
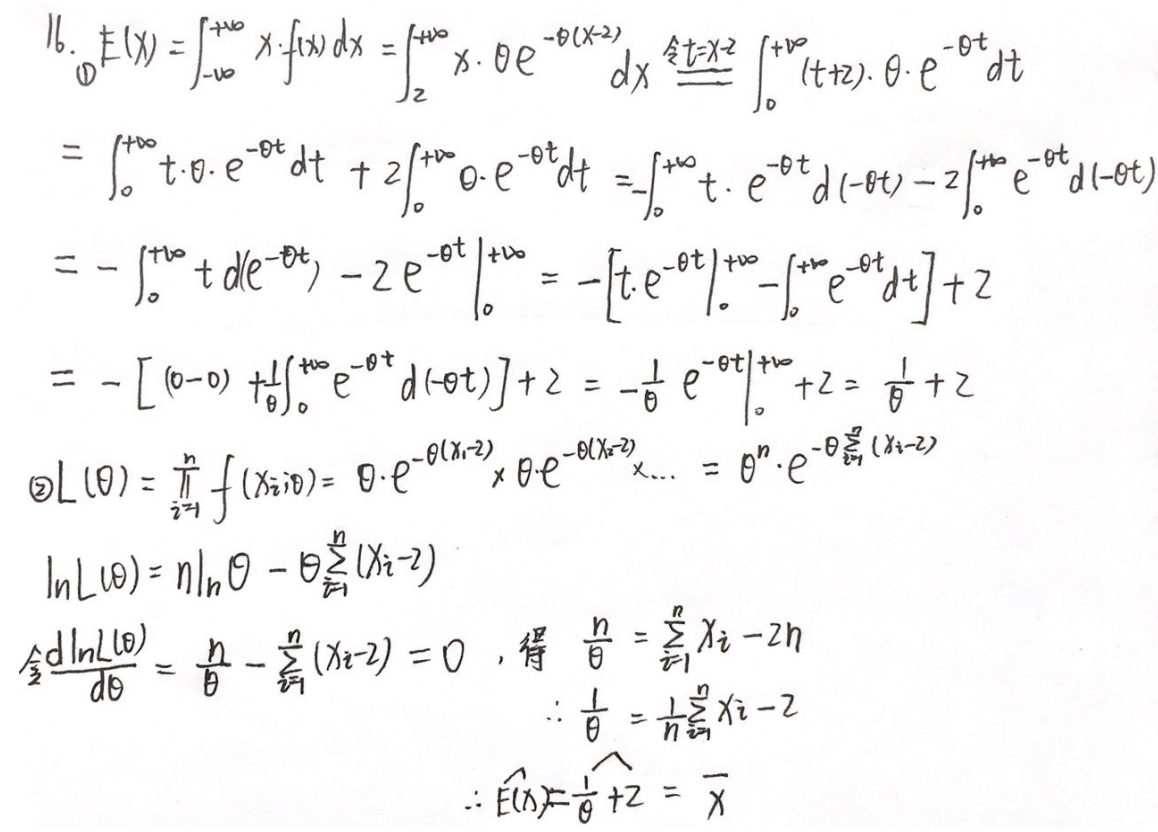
答案: X ˉ \bar{X} Xˉ
习题2:23李林四(二)16.
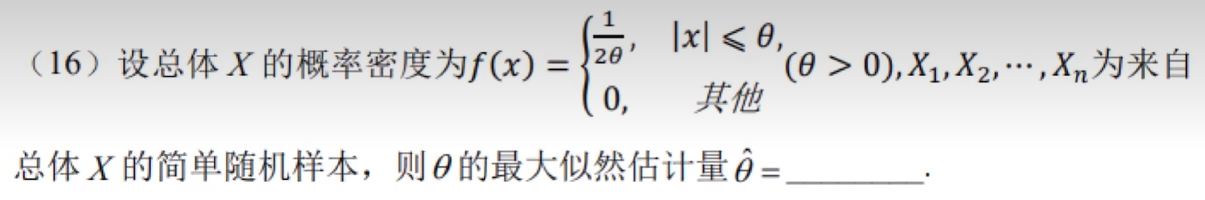
分析:∵|x|≤θ ∴θ的最大似然估计量为 θ ^ \hat{θ} θ^=max{|X₁|,|X₂|,…,|Xn|}
答案:max{|X₁|,|X₂|,…,|Xn|}
习题3:23李林六套卷(六)16. 二维随机变量求θ的最大似然估计

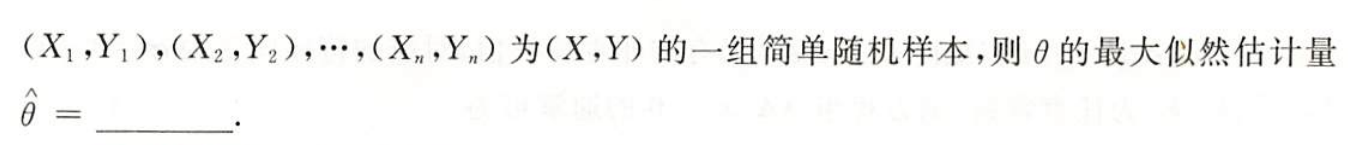
分析:

答案: 1 2 n ∑ i = 1 n ( X i + Y i ) \dfrac{1}{2n}\sum\limits_{i=1}^n(X_i+Y_i) 2n1i=1∑n(Xi+Yi)
习题4:22年22. 两个随机变量,求最大似然估计量

答案:

7.2 评价估计量优良性的标准
(1)无偏性 (无偏估计)
若参数θ的估计量 θ ^ = θ ^ ( X 1 , X 2 , . . . , X n ) \hat{θ}=\hat{θ}(X_1,X_2,...,X_n) θ^=θ^(X1,X2,...,Xn)对一切n及θ∈I,有 E ( θ ^ ) = θ E(\hat{θ})=θ E(θ^)=θ,则称 θ ^ \hat{θ} θ^为 θ θ θ的无偏估计量
即若 θ ^ \hat{θ} θ^是θ的无偏估计量,则 E ( θ ^ ) = θ E(\hat{θ})=θ E(θ^)=θ
E ( X ˉ ) = μ = E ( X ) , E ( S 2 ) = σ 2 = D ( X ) E(\bar X)=μ=E(X),E(S^2)=σ²=D(X) E(Xˉ)=μ=E(X),E(S2)=σ2=D(X)
(2)有效性
有效性(最小方差性):都是无偏估计量的情况下,方差小的更有效

(3)一致性
一致性(相合性): θ ^ → P θ \hat{θ}\xrightarrow{P}θ θ^Pθ,依概率收敛

例题1:14年14.

分析:
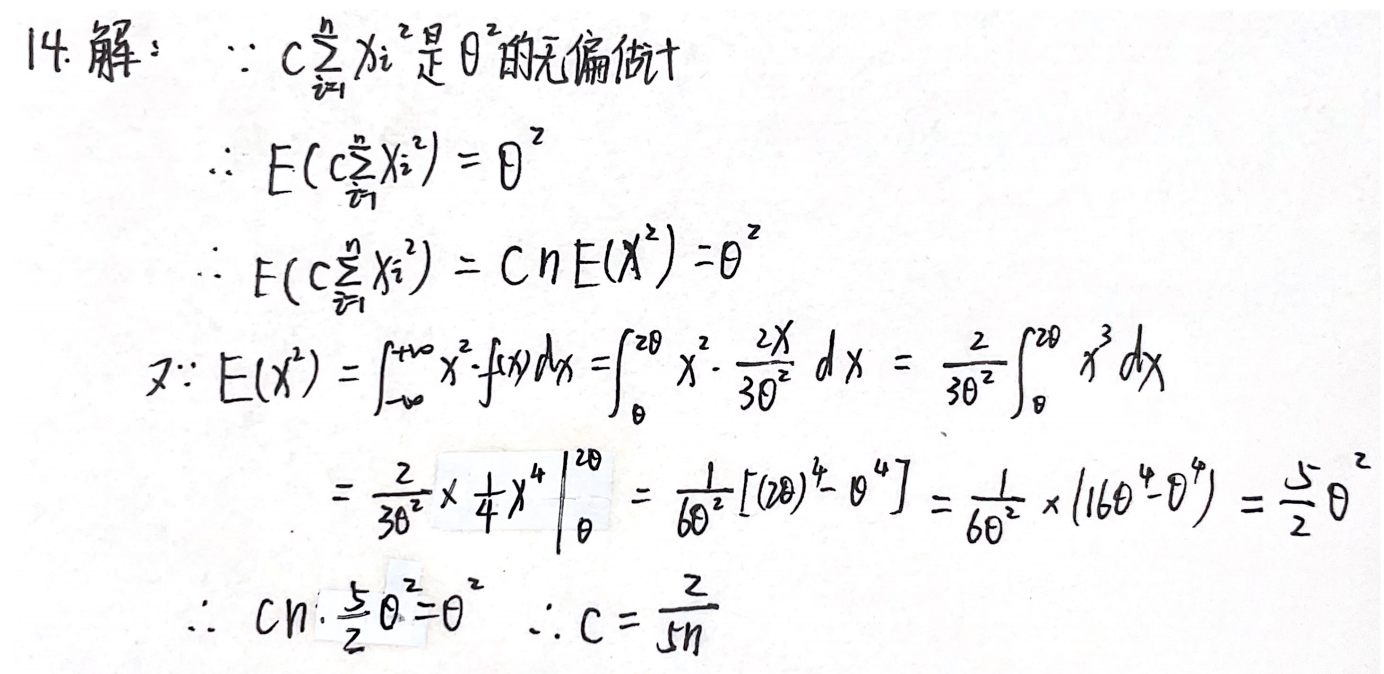
答案: 2 5 n \dfrac{2}{5n} 5n2
例题2:09年14. 无偏估计、二项分布的数字特征
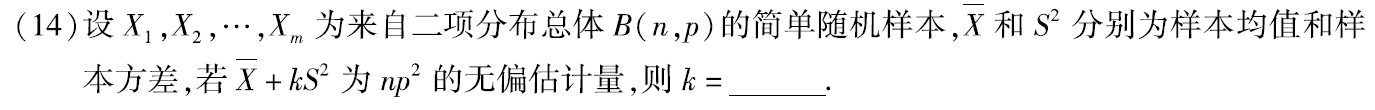
分析: θ ^ \hat{θ} θ^是θ的无偏估计量: E ( θ ^ ) = θ E(\hat{θ})=θ E(θ^)=θ。 E ( X ˉ ) = μ = E ( X ) , E ( S 2 ) = σ 2 = D ( X ) E(\bar X)=μ=E(X),E(S^2)=σ²=D(X) E(Xˉ)=μ=E(X),E(S2)=σ2=D(X)
则 E ( X ˉ + k S 2 ) = n p 2 E(\bar X+kS^2)=np^2 E(Xˉ+kS2)=np2,即 E ( X ˉ ) + k E ( S 2 ) = n p + k n p ( 1 − p ) = n p 2 E(\bar X)+kE(S^2)=np+knp(1-p)=np^2 E(Xˉ)+kE(S2)=np+knp(1−p)=np2,化简得 k=-1
答案:-1
例题3:16年23(2)
例题4:12年23(3)
7.3 区间估计
1.置信区间、置信度
P { θ 1 < θ < θ 2 } = 1 − α P\{θ_1<θ<θ_2\}=1-α P{θ1<θ<θ2}=1−α
1 − α 1-α 1−α称为置信度(置信水平), α α α称为显著性水平
区间 ( θ 1 , θ 2 ) (θ_1,θ_2) (θ1,θ2)称为参数θ的置信度为1-α的置信区间。 θ 1 θ₁ θ1和 θ 2 θ₂ θ2分别称为置信度为 1 − α 1-α 1−α的置信区间的置信下限和置信上限;
2.求μ的置信区间
正态总体均值μ的置信区间(置信水平为1-α)
| 待估参数 | 其他参数 | 枢轴量的分布 | 置信区间 |
|---|---|---|---|
| μ | σ²已知 | Z = X ‾ − μ σ / n ∼ N ( 0 , 1 ) Z=\dfrac{\overline{X}-μ}{σ/\sqrt{n}}\sim N(0,1) Z=σ/nX−μ∼N(0,1) | ( X ‾ − Z α 2 σ n , X ‾ + Z α 2 σ n ) (\overline{X}-Z_{\frac{α}{2}}\dfrac{σ}{\sqrt{n}},\overline{X}+Z_{\frac{α}{2}}\dfrac{σ}{\sqrt{n}}) (X−Z2αnσ,X+Z2αnσ) |
| μ | σ²未知 | t = X ‾ − μ S / n ∼ t ( n − 1 ) t=\dfrac{\overline{X}-μ}{S/\sqrt{n}}\sim t(n-1) t=S/nX−μ∼t(n−1) | ( X ‾ − t α 2 ( n − 1 ) S n , X ‾ + t α 2 ( n − 1 ) S n ) (\overline{X}-t_{\frac{α}{2}}(n-1)\dfrac{S}{\sqrt{n}},\overline{X}+t_{\frac{α}{2}}(n-1)\dfrac{S}{\sqrt{n}}) (X−t2α(n−1)nS,X+t2α(n−1)nS) |
例题1:16年14. 置信区间、置信上限

分析:置信区间是以 X ˉ \bar{X} Xˉ为中心对称的
X ˉ = 9.5 \bar{X}=9.5 Xˉ=9.5, X ˉ \bar{X} Xˉ到置信下限是1.3,则 X ˉ \bar{X} Xˉ到置信上限也是1.3
答案: ( 8.2 , 10.8 ) (8.2,10.8) (8.2,10.8)
例题2:03年6.

分析:
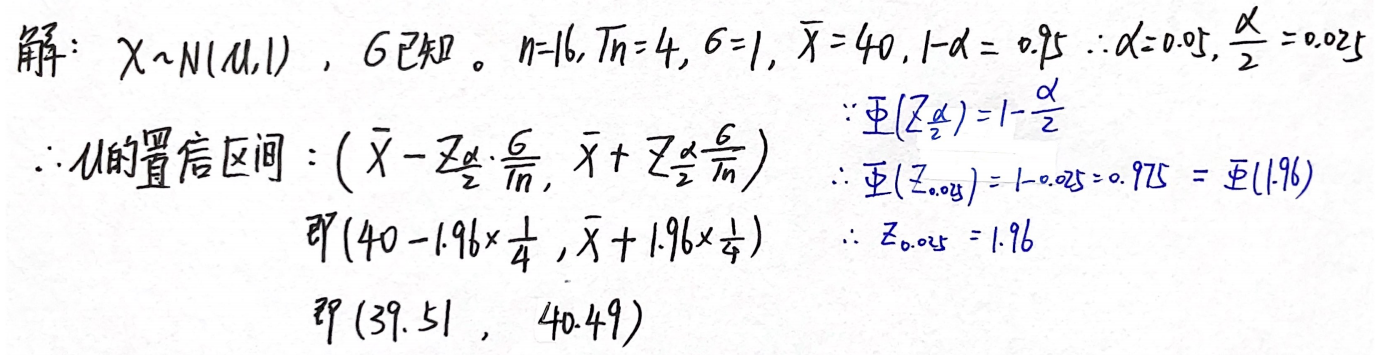
答案: ( 39.51 , 40.49 ) (39.51,40.49) (39.51,40.49)
Ch8. 假设检验
1.拒绝域α、接受域1-α、H₀原假设、H₁备择假设
检验水平(显著性水平)α,即为拒绝域面积。α越小,接受域越大。
例题1:18年8. 假设检验

分析:α为拒绝域。若拒绝,说明落在α内。若接受,说明落在α外。
答案:D
2.双边检验、单边检验
①接受域看H₀,拒绝域看H₁
②易错点:求未知数时,要代入原假设H₀中μ的值 μ 0 μ_0 μ0
(1)双边检验:
①H₀:μ=μ₀,H₁:μ≠μ₀
②α/2
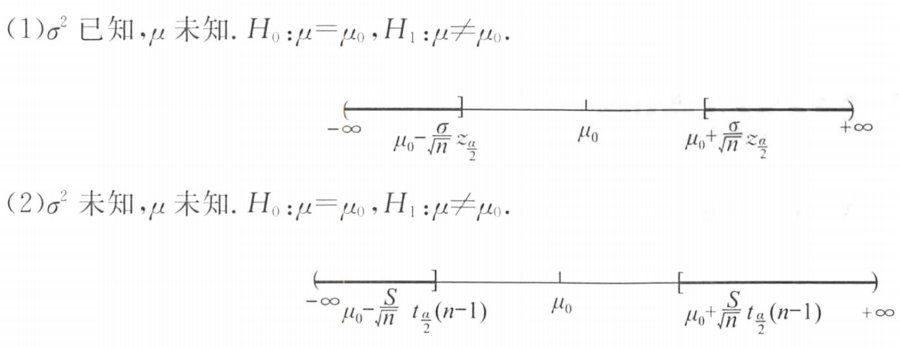
(2)单边检验:
①H₀:μ≥或≤μ₀,H₁:μ>或<μ₀
②α

例题1:

分析:

答案:求出拒绝域,得 x ˉ = 10 \bar{x}=10 xˉ=10落入拒绝域,拒绝原假设H₀
3.第一类错误、第二类错误
1.犯第一类错误(弃真):H₀为真的情况下,拒绝了H₀。
犯第一类错误的概率: α = P { 拒绝了 H 0 ∣ H 0 为真 } = P { 落在拒绝域 } α=P\{拒绝了H_0|H_0为真 \}=P\{落在拒绝域\} α=P{拒绝了H0∣H0为真}=P{落在拒绝域}
2.犯第二类错误(取伪):H₀为假的情况下,接受了H₀。
犯第二类错误的概率: β = P { 接受了 H 0 ∣ H 0 为假 } = P { 落在接受域 } β=P\{接受了H_0|H_0为假\}=P\{落在接受域\} β=P{接受了H0∣H0为假}=P{落在接受域}
常用性质:
① P { x > a } = 1 − P { x ≤ a } P\{x>a\}=1-P\{x≤a\} P{x>a}=1−P{x≤a}
② Φ ( − x ) = 1 − Φ ( x ) Φ(-x)=1-Φ(x) Φ(−x)=1−Φ(x)
例题1:23李林六套卷(四)10. 犯第一类错误

分析:

答案:C
例题2:21年10. 犯第二类错误

分析:

答案:B
例题3:


分析:
犯第一类错误的概率α = P{H0为真,落在拒绝域}
犯第二类错误的概率β=P{H1为真,落在接受域}
答案:
相关文章:
概率论与数理统计:第七章:参数估计 第八章:假设检验
文章目录 Ch7. 参数估计7.1 点估计1.矩估计2.最大似然估计(1)离散型(2)连续型 7.2 评价估计量优良性的标准(1)无偏性 (无偏估计)(2)有效性(3)一致性 7.3 区间估计1.置信区间、置信度2.求μ的置信区间 Ch8. 假设检验1.拒绝域α、接受域1-α、H₀原假设、H₁备择假设2.双边检验、…...

【Kubernetes】Kubernetes的监控工具Promethues
Prometheus 一、Prometheus 概念1. Prometheus 概述2. Prometheus 的监控数据3. Prometheus 的特点4. Prometheus 和 zabbix 区别5. Prometheus 的生态组件5.1 Prometheus server5.2 Client Library5.3 Exporters5.4 Service Discovery5.5 Alertmanager5.6 Pushgateway5.7 Graf…...
【linux】2 Linux编译器-gcc/g++和Linux调试器-gdb
文章目录 一、Linux编译器-gcc/g使用1.1 背景知识1.2 gcc如何完成1.3 函数库1.4 gcc选项 二、linux调试器-gdb使用2.1 背景2.2 开始使用 总结 ヾ(๑╹◡╹)ノ" 人总要为过去的懒惰而付出代价ヾ(๑╹◡╹)ノ" 一、Linux编译器-gcc/g使用 1.1 背景…...
【力扣每日一题】2023.8.17 切披萨的方案数
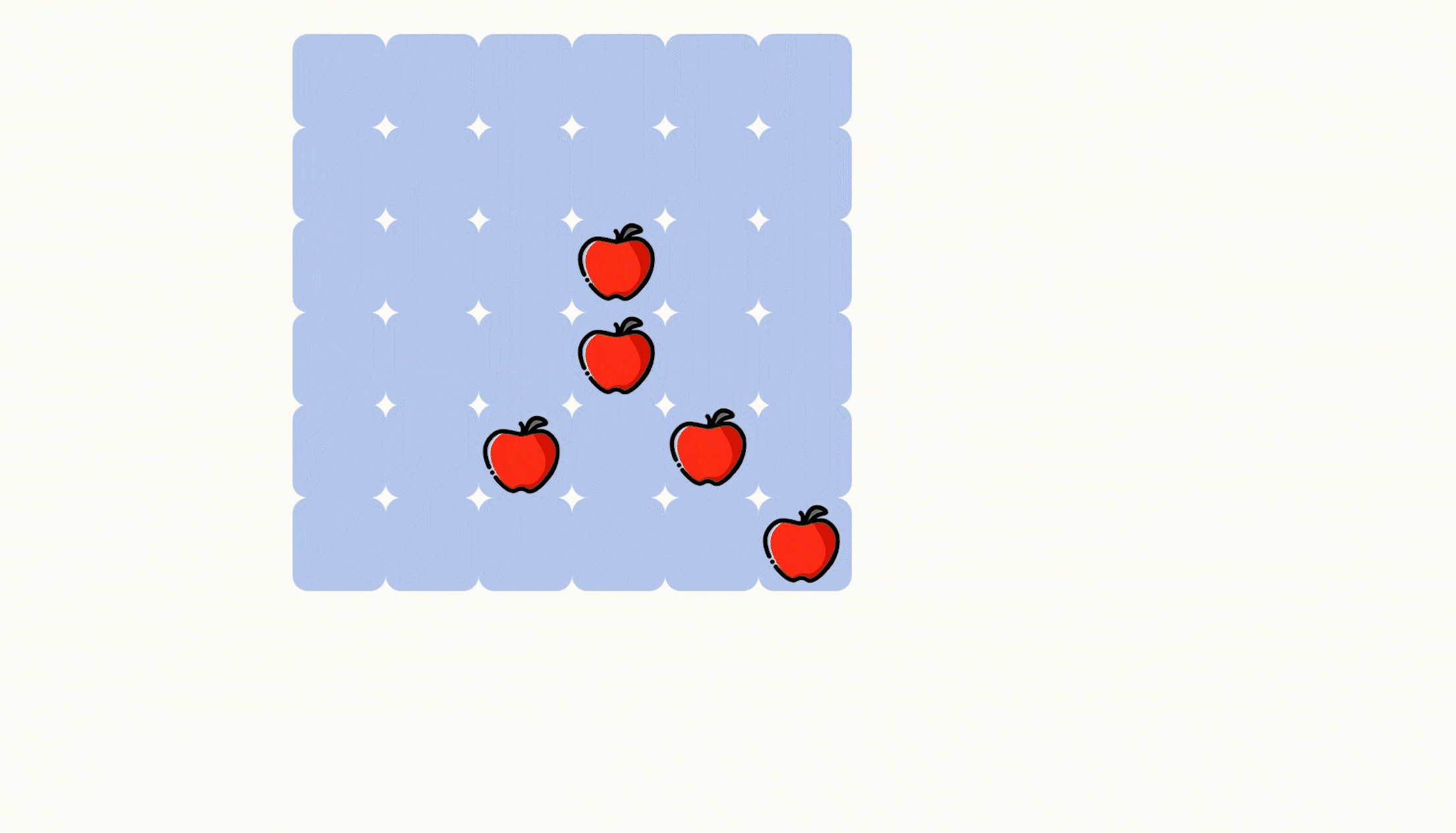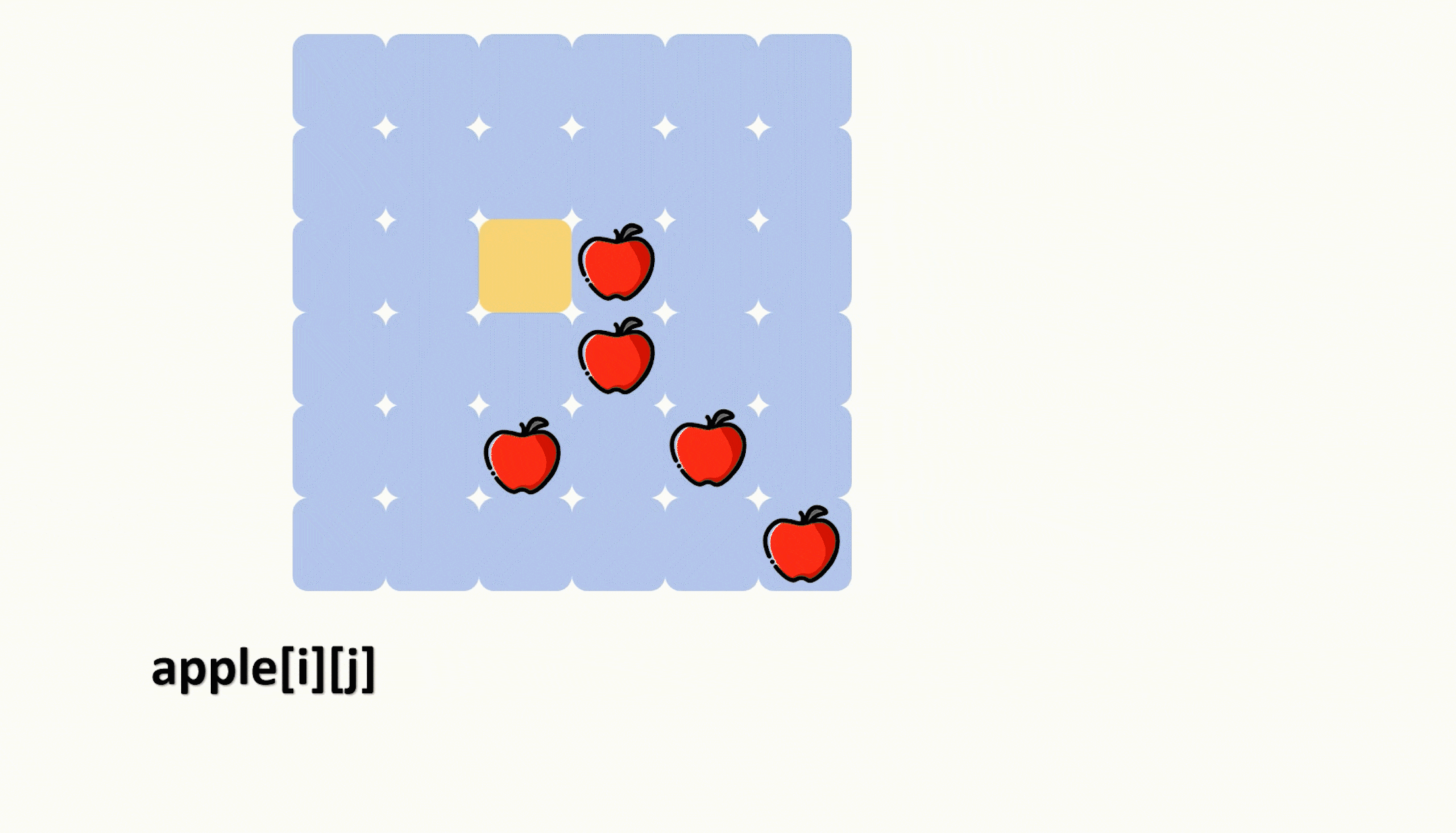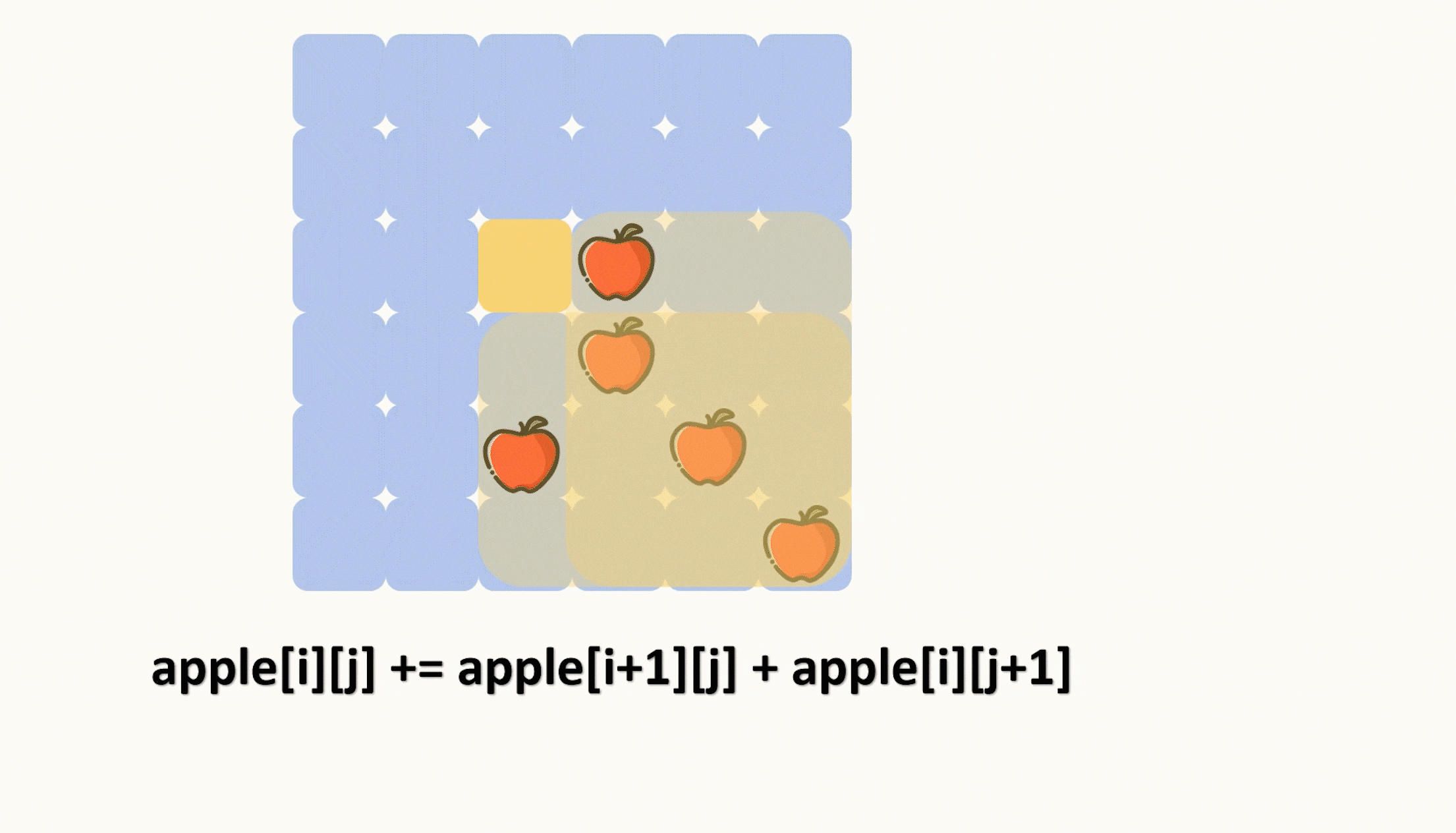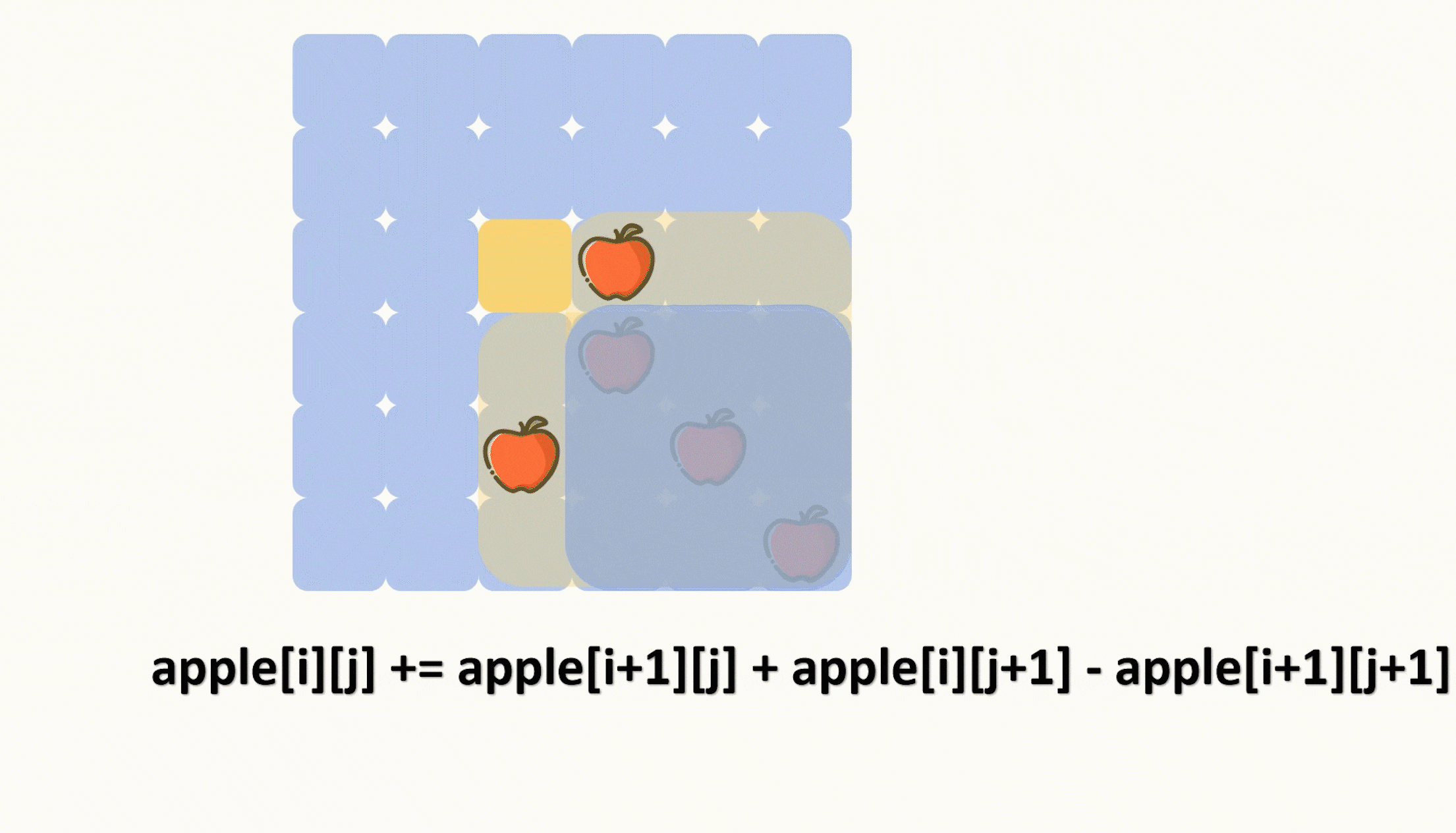
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 题目给我们一个二维数组来表示一个披萨,其中‘A’表示披萨上的苹果。 让我们切k-1刀,把披萨切成 k 份࿰…...

Linux调试器-gdb使用
1. 背景 程序的发布方式有两种, debug 模式和 release 模式 Linux gcc/g 出来的二进制程序,默认是 release 模式 要使用 gdb 调试,必须在源代码生成二进制程序的时候 , 加上 - g 选项 2. 开始使用 gdb binFile 退出: ct…...

linux安装mysql错误处理
linux下mysql的安装与使用 linux安装mysql可有三种方式: 1、yum安装 2、源码安装 3、glibc安装 安装wget yum install -y wget https://blog.csdn.net/darendu/article/details/89874564?utm_sourceapp Linux上error while loading shared libraries问题解决方法…...
Matlab绘制灰度直方图
直方图是根据灰图像绘制的,而不是彩色图像通。查看图像直方图时候,需要先确定图片是否为灰度图,使用MATLAB2019查看图片是否是灰度图片,在读取图片后在MATLAB界面的工作区会显示读取的图像矩阵,如果是,那么…...

http学习笔记1
图解HTTP学习笔记 1.2 HTTP的诞生 CERN(欧洲核子研究组织)的蒂姆 • 伯纳斯 - 李(Tim BernersLee)博士提出了一种能让远隔两地的研究者们共享知识的设想。最初设想的基本理念是:借助多文档之间相互关联形成的超文本&am…...

PDF文件分割合并
PDF文件的分割和合并代码。 from PyPDF2 import PdfFileReader,PdfFileWriterdef pdf_split(filename,outputname)pr PdfFileReader(filename)for page in range(p.getNumPages()):pw PdfFileWriter()pw.addPage(pr.getPage(page))with open(f{outputname}{page}.pdf,wb) as…...

物联网无线通信方式总结
本文主要内容(一些物联网无线通信方式) 本文将介绍一些物联网无线通信方式的技术特点、底层调制方式和主要应用场景物联网无线通信方式是指利用无线技术实现物体之间的信息交换和网络连接的方式物联网无线通信方式的选择需要考虑多种因素,如传输距离、功耗、数据速…...
计算机竞赛 python的搜索引擎系统设计与实现
0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 python的搜索引擎系统设计与实现 🥇学长这里给一个题目综合评分(每项满分5分) 难度系数:3分工作量:5分创新点:3分 该项目较为新颖ÿ…...

ue5 场景搭建和灯光照明参考
https://www.youtube.com/watch?vOCgn40aWVuU https://www.youtube.com/watch?vIGLujClhL5U...

Mycat跨分片Join指南
前言Mycat目前版本支持跨分片的join,主要实现的方式有四种。 全局表 ER分片 HBT ShareJoin ShareJoin在开发版中支持,前面三种方式1.3.0.1支持 2.ShareJoin ShareJoin是一个简单的跨分片Join,基于HBT的方式实现。 目前支持2个表的join,原理就是解析SQL语句,拆分成单表的…...

网络:RIP协议
1. RIP协议原理介绍 RIP是一种比较简单的内部网关协议(IGP协议),RIP基于距离矢量的贝尔曼-福特算法(Bellman - Ford)来计算到达目的网络的最佳路径。最初的RIP协议开发时间较早,所以在带宽、配置和管理方面的要求也较低。 路由器运…...

如何优化因为高亮造成的大文本(大字段)检索缓慢问题
首先还是说一下背景,工作中用到了 elasticsearch 的检索以及高亮展示,但是索引中的content字段是读取的大文本内容,所以后果就是索引的单个字段很大,造成单独检索请求的时候速度还可以,但是加入高亮之后检索请求的耗时…...

HTML <table> 标签
实例 一个简单的 HTML 表格,包含两行两列: <table border="1"><tr><th>Month</th><th>Savings</th></tr><tr><td>January</td><td>$100</td></tr> </table>定义和用法 &l…...
ubuntu pdf阅读器okular
sudo apt-get install okular安装完毕后,使用如下命令浏览pdf文档 okular xxx.pdf...

根据源码,模拟实现 RabbitMQ - 虚拟主机 + Consume设计 (7)
目录 一、虚拟主机 Consume设计 1.1、承接问题 1.2、具体实现 1.2.1、消费者订阅消息实现思路 1.2.2、消费者描述自己执行任务方式实现思路 1.2.3、消息推送给消费者实现思路 1.2.4、消息确认 一、虚拟主机 Consume设计 1.1、承接问题 前面已经实现了虚拟主机大部分功…...

docker中bridge、host、container、none四种网络模式简介
目录 一.bridge模式 1.简介 2.演示 (1)运行两个容器,不指定网络模式情况下默认是bridge模式 (2)在主机中自动生成了两个veth设备 (3)查看两个容器的IP地址 (4)可以…...
排序算法之详解冒泡排序
引入 冒泡排序顾名思义,就是像冒泡一样,泡泡在水里慢慢升上来,由小变大。虽然冒泡排序和冒泡并不完全一样,但却可以帮助我们理解冒泡排序。 思路 一组无序的数组,要求我们从小到大排列 我们可以先将最大的元素放在数组…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...
