牛客复盘] 2023河南萌新联赛第(七)场:信息工程大学 B\I 20230823
牛客复盘] 2023河南萌新联赛第(七)场:信息工程大学 B\I 20230823
- 总结
- B 七夕
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- I 细胞分裂
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 六、参考链接
总结
- 场外OB做了B和I题,只能说这场有点离谱。
- B 并查集缩点+图的直径(max(最短路))
- I 分解质因数贪心(二分也可以)
- 另外据说C题也离谱,出题人拿洛谷第一篇题解造的数据,但那篇题解是错的,评论区有人hack了给出反例。
B 七夕
链接: 七夕
1. 题目描述

2. 思路分析
这题描述挺清晰的,可惜说反了。正确的表述可以看我代码里的注释。
一个错误的思路是直接0-1bfs,但题目没给起始点,起始和结束可以是最坏点,所以不能做。实际题目要求的是最长路(最坏)。
- 先用dsu缩点,如果两个城市可以用城际公交到达,那么这俩可以看做一个城市,没有移动代价。
- 于是很容易想到用并查集把所有城市合并成一个一个城市群,再把城市群作为图里的节点。
- 那么问题就转化成城市群这个图的最长路,这个实际上是图的直径,可以用两次bfs的方法做。
- 结论:从任意一点出发bfs,最远端的点,一定是一条直径的一个端点。
- 那么就可以第一次bfs求一个端点;第二次求直径长度。
- 代码实现时,把节点-1转化成0-indexed。
- 缩点后,用每个家族的代表元参与城市群的建图。
3. 代码实现
PROBLEM = """链接:https://ac.nowcoder.com/acm/contest/63746/B七夕节左近,楚楚想去见女朋友,可是他最近和女朋友吵架了,女朋友躲着他,不知道会出现在哪座城市里。楚楚心知肚明女朋友是在赌气,所以无论自己在哪座城市,女朋友在哪座城市,
他一定要在七夕节见到她。城市之间用铁路或者城际公交中的一种相连通,虽然并不是任意两个城市都直接相连,但是保证可以通过这两种交通方式从任一城市出发到另一任意城市。
由于楚楚的特殊身份,他可以免费乘坐城际公交,那么他最少需要买多少张火车票才能保证见到女朋友呢?
输入描述:
第一行三个整数n,k,m,表示共n个城市,编号从1到n,k条城际,m条铁路。
接下来k行,每行两个整数u、v,表示城市u、v之间有城际。
再接下来m行,每行两个整数u、v,表示城市u、v之间有铁路。输出描述:
一个整数表示还需要的票数。
输入
6 3 4
1 2
2 3
4 5
1 3
3 4
4 6
5 6输出
2
"""# ms
def solve():n, k, m = RI()fa = list(range(n))def find(x):t = xwhile x != fa[x]:x = fa[x]while t != x:t, fa[t] = fa[t], xreturn xfor _ in range(k): # 读k个城际,缩点u, v = RI()u, v = find(u - 1), find(v - 1)fa[u] = vg = [[] for _ in range(n)]for _ in range(m): # 读m个铁道,给代表元建图;重边和自环都不管,直接建u, v = RI()u, v = find(u - 1), find(v - 1)g[u].append(v)g[v].append(u)def bfs(st): # 层序遍历q = [st]vis = [0] * nvis[st] = 1step = 0while q:nq = []step += 1for u in q:for v in g[u]:if not vis[v]:vis[v] = 1nq.append(v)q = nqreturn u, step - 1 # 两次bfs求图的直径,就是max(最短路)st, _ = bfs(find(0)) # 第一次bfs求直径的一段_, ans = bfs(st) # 第二次bfs求直径长度print(ans)
I 细胞分裂
链接: 细胞分裂
1. 题目描述
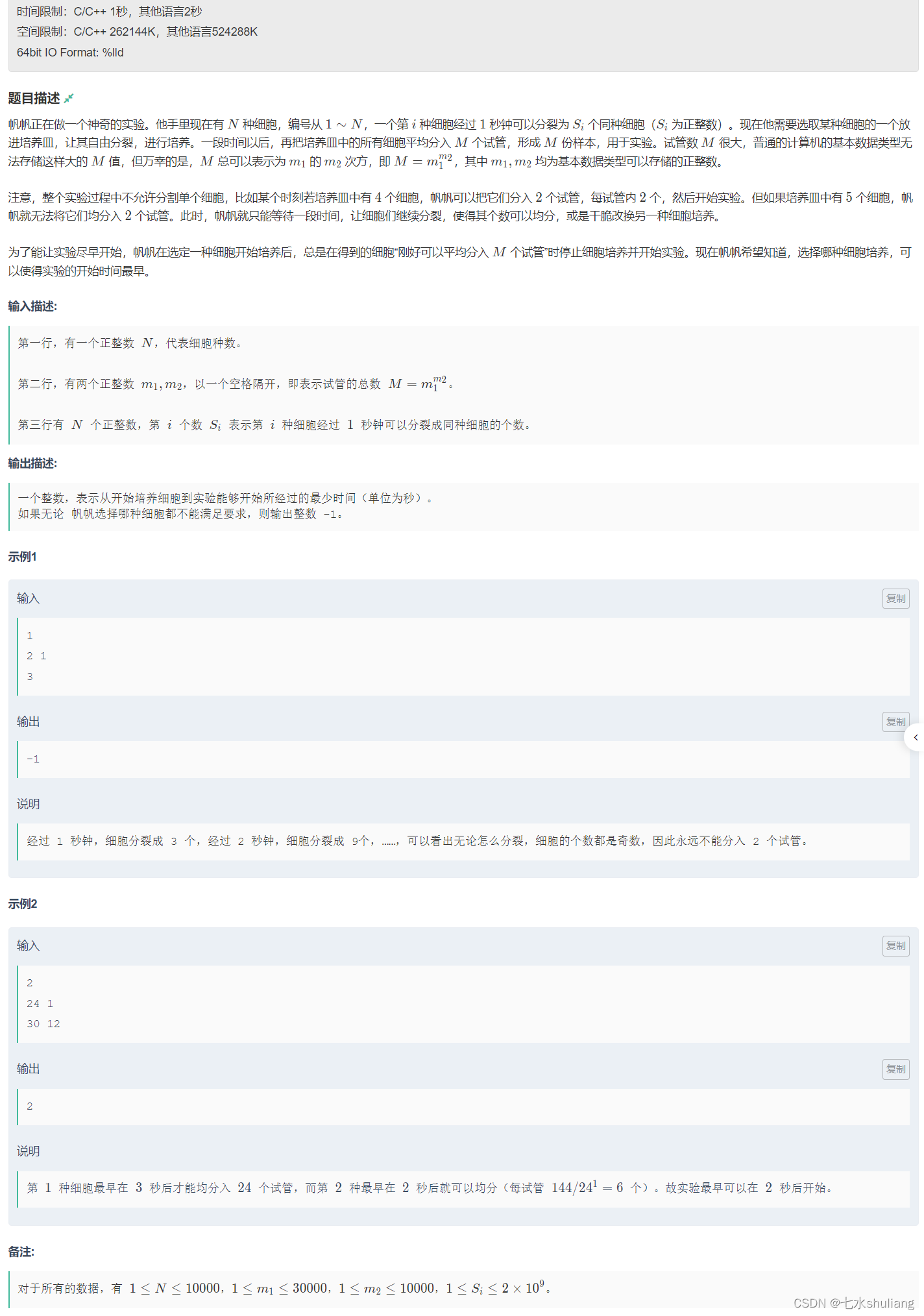
2. 思路分析
一眼贪心,然而提交wa。
赛中一众大佬都过不了,赛后看ac的代码,全都长得一样而且相当复杂,连注释都没改,经神秘群友调查,发现出自隔壁一篇csdn。
另外由于这是一道原题,在洛谷和其他oj网站上提交自己代码都能过,就牛客过不了。
赛后有群友爆出了wa的数据,经人工验证(或者用大数代码验证),那篇复杂代码的解是错的。
输入
1
39102 255398
657695640
正确输出
255398
错误ac代码输出
85133print((657695640**85133) % (39102**255398) == 0) # False
3. 代码实现
def solve():n, = RI()m1, m2 = RI()a = RILST()cnt = [(p, v * m2) for p, v in pt.prime_factorization(m1)] # 对m1分解质因数计数if m1 == 1:return print(0)ans = inffor s in a:p = 0for k, v in cnt: # s要包含m1的每个质因数,且要扩展次数达到目标次,向上取整c = 0while s % k == 0:s //= kc += 1if c == 0: # 不含breakp = max(p, (v + c - 1) // c) # 向上取整else:ans = min(ans, p) # 没有不含的才能用print([ans, -1][ans == inf])
六、参考链接
- 无
相关文章:

牛客复盘] 2023河南萌新联赛第(七)场:信息工程大学 B\I 20230823
牛客复盘] 2023河南萌新联赛第(七)场:信息工程大学 B\I 20230823 总结B 七夕1. 题目描述2. 思路分析3. 代码实现 I 细胞分裂1. 题目描述2. 思路分析3. 代码实现 六、参考链接 总结 场外OB做了B和I题,只能说这场有点离谱。B 并查…...

使用PyMuPDF添加PDF水印
使用Python添加PDF水印的博客文章。 C:\pythoncode\new\pdfwatermark.py 使用Python在PDF中添加水印 在日常工作中,我们经常需要对PDF文件进行处理。其中一项常见的需求是向PDF文件添加水印,以保护文件的版权或标识文件的来源。本文将介绍如何使用Py…...
window如何实时刷新日志文件
1 安装windows git 下载地址:Git - Downloading Package (git-scm.com) 2 打开git bash 输入tail.exe -f 日志文件路径...
-Demo)
动态代理的两个使用方式(手动实现+SpringAOP实现)-Demo
一、手动实现 1、具体代码 package com.xch.proxy;/*** 具体业务接口** author XuChenghe* date 2023/8/18 15:09*/ public interface Star {/*** 唱歌方法** param name* return*/String sing(String name);/*** 跳舞方法*/void dance();} package com.xch.proxy;/*** 具体…...
)
面试话术(MQ+mybatis+nginx+redis+ssm+mysql+linux)
面试话术 RabbitMq1、介绍一下rabbitmq2、如何保证消息确定消息发送成功,并且被消费成功,有什么保障措施3、如何保证消息不被重复消费4、RabbitMQ 宕机了怎么处理 授权话术1、你给我说一下授权认证(登陆注册)的逻辑2、说一下jwt3、…...

JSON的理解
文章目录 1、什么是JSON2、为什么要用JSON3、JSON的格式规定3.1 对象(0bject):对应着JS中的对象3.2 数组(Array):对应着JS中的数组形式3.3 简单形式:对应着JS中的基础数据类型 4、JSON和Js的转换5、JSON对象…...

面试热题(二叉树的最大路径)
路径 被定义为一条从树中任意节点出发,沿父节点-子节点连接,达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。 路径和 是路径中各节点值的总和。 给定一个二叉树的根节点 root…...

C#设计模式之--六大原则 开闭原则
设计模式六大原则是单一职责原则、里氏替换原则、依赖倒置原则、接口隔离原则、迪米特法则、开闭原则。它们不是要我们刻板的遵守,而是根据实际需要灵活运用。只要对它们的遵守程度在一个合理的范围内,努为做到一个良好的设计。本文主要介绍一下.NET(C#)…...
编写Dockerfile制作自己的镜像并推送到私有仓库
说明:我将用到的私有仓库是Harbor,安装教程参考我的这一篇文章: 安装搭建私有仓库Harbor_Word_Smith_的博客-CSDN博客 一、案例1 1、要求 编写Dockerfile制作Web应用系统nginx镜像,生成镜像nginx:v1.1,并推送其到私…...

华为OD-分积木/分苹果
题目描述 哥哥弟弟分一堆积木,每块积木重量不同。弟弟要求平分两组,每组数量可以不同但总重量必须相等。 然而弟弟只会二进制并且加法不进位。例如三块积木 3,5,6 分成两组 [3] 和 [5,6] 弟弟认为 5(二进制1001)加上6(…...

Mysql的引擎有哪些?支持事物么?DB储存引擎有哪些?
Mysql的引擎有哪些?支持事物么?DB储存引擎有哪些? MySQL有多种存储引擎,每种存储引擎有各自的优缺点,可以择优选择使用: MyISAM、InnoDB、MERGE、MEMORY(HEAP)、BDB(BerkeleyDB)、EXAMPLE、FEDERATED、ARCH…...

【懒加载】js实现懒加载、vue实现图片懒加载指令
懒加载 延迟加载,对于一个很长的页面,优先加载可视区域的内容,其他部分等进入可视区域时再加载 懒加载作用 是一种网页性能优化的方式,它能极大的提升用户体验。比如一个页面中有很多图片,但是首屏只出现几张&#…...
)
微信小程序教学系列(7)
第七章:小程序安全和权限管理 第一节:小程序安全性保障 在开发小程序时,我们要时刻牢记小程序的安全性。毕竟,我们可不希望我们的小程序被黑客入侵或者用户的隐私被泄露。所以,让我们一起来了解一下如何保障小程序的…...

Android 9.0 kenel和frameworks中修改ram运行内存的功能实现
1.前言 在9.0的系统rom产品开发定制中,在对一些产品开发中的配置需求方面,在产品后续订单中,在某些机型中需要升级下系统内核配置,项目时间比较仓促,所以 来不及对硬件重新定制,就需要软件方面在ram运行内存的容量大小方面作假,修改ram真实的大小容量,所以就需要在ken…...

PHP实践:获取网络上图片的长宽以及图片类型
🏆作者简介,黑夜开发者,全栈领域新星创作者✌,CSDN博客专家,阿里云社区专家博主,2023年6月CSDN上海赛道top4。 🏆数年电商行业从业经验,历任核心研发工程师,项目技术负责…...

使用 DPO 微调 Llama 2
简介 基于人类反馈的强化学习 (Reinforcement Learning from Human Feedback,RLHF) 事实上已成为 GPT-4 或 Claude 等 LLM 训练的最后一步,它可以确保语言模型的输出符合人类在闲聊或安全性等方面的期望。然而,它也给 NLP 引入了一些 RL 相关…...
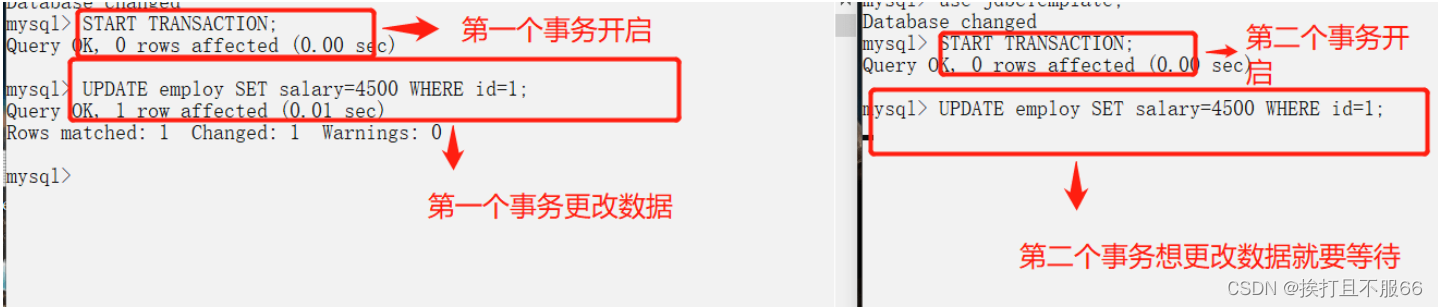
数据库——事务,事务隔离级别
文章目录 什么是事务?事务的特性(ACID)并发事务带来的问题事务隔离级别实际情况演示脏读(读未提交)避免脏读(读已提交)不可重复读可重复读防止幻读(可串行化) 什么是事务? 事务是逻辑上的一组操作,要么都执行,要么都不执行。 事务最经典也经常被拿出…...
对《VB.NET通过VB6 ActiveX DLL调用PowerBasic及FreeBasic动态库》的改进
《VB.NET通过VB6 ActiveX DLL调用PowerBasic及FreeBasic动态库》使用的Activex DLL公共对象是需要先注册的。https://blog.csdn.net/weixin_45707491/article/details/132437502?spm1001.2014.3001.5501 Activex DLL事前注册,一次多用说起来也不是啥大问题&#x…...

【PHP】数据类型运算符位运算
文章目录 数据类型简单(基本)数据类型:4个小类复合数据类型:2个小类特殊数据类型:2个小类类型转换类型判断整数类型浮点类型布尔类型 运算符赋值运算符算术运算符比较运算符逻辑运算符连接运算符错误抑制符三目运算符自…...

使用 Nacos 作为 Spring Boot 配置中心
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...
