[Go版]算法通关村第十三关黄金——数字数学问题之数论问题(最大公约数、素数、埃氏筛、丑数)
目录
- 题目:辗转相除法(求最大公约数)
- 思路分析:辗转相除法(也叫欧几里得算法)`gcd(a,b) = gcd(b,a mod b)`
- 复杂度:时间复杂度 O ( n + l o g ( m a x ) ) O(n+log(max)) O(n+log(max))、空间复杂度 O ( 1 ) O(1) O(1)
- Go代码
- 题目:判断是否是素数
- 思路分析:判断n是否是素数只需测试 2 到 sqrtN 的所有可能因子 + "6K +1/-1" 规则
- 复杂度:时间复杂度 O ( s q r t ( n ) ) O(sqrt(n)) O(sqrt(n))、空间复杂度 O ( 1 ) O(1) O(1)
- Go代码
- 题目:埃氏筛
- 思路分析:埃氏筛法思想,逐步排除掉不是质数的数
- 复杂度:时间复杂度 O ( n l o g l o g n ) O(n log log n) O(nloglogn)、空间复杂度 O ( n ) O(n) O(n)
- Go代码
- 题目:判断是不是丑数
- 思路分析:循环除2 3 5 判断最后值是否==1
- 复杂度:时间复杂度 O ( l o g n ) O(log n) O(logn)、空间复杂度 O ( 1 ) O(1) O(1)
- Go代码
题目:辗转相除法(求最大公约数)
题目链接:LeetCode-1979. 找出数组的最大公约数

思路分析:辗转相除法(也叫欧几里得算法)gcd(a,b) = gcd(b,a mod b)
辗转相除法其核心部分为:若r 是a ÷ b的余数,则 gcd(a, b)=gcd(b, r)
复杂度:时间复杂度 O ( n + l o g ( m a x ) ) O(n+log(max)) O(n+log(max))、空间复杂度 O ( 1 ) O(1) O(1)
Go代码
func findGCD(nums []int) int {max, min := getMaxMin(nums)return getGcd(max, min)
}
// gcd求最大公约数
func getGcd(a int, b int) int {yu := 0for b != 0 {yu = a % b //得到余数a = b //根据辗转相除法,把被除数赋给除数b = yu //余数赋给被除数}return a //返回除数
}
func getMaxMin(nums []int) (max int, min int) {max, min = nums[0], nums[0]length := len(nums)for i:=1; i<length; i++ {if nums[i] > max {max = nums[i]}if nums[i] < min {min = nums[i]}}return
}
题目:判断是否是素数
思路分析:判断n是否是素数只需测试 2 到 sqrtN 的所有可能因子 + “6K +1/-1” 规则
复杂度:时间复杂度 O ( s q r t ( n ) ) O(sqrt(n)) O(sqrt(n))、空间复杂度 O ( 1 ) O(1) O(1)
Go代码
func isPrimes(n int) bool {if n <= 1 {return false}if n <= 3 {return true}if n%2==0 || n%3==0 {return false}// 判断n是否是素数时,只需要测试 2 到 sqrtN 的所有可能因子// max := int(math.Pow(float64(n), 0.5))max := int(math.Sqrt(float64(n)))// 根据 "6K +1/-1" 规则for i:=5; i<=max; i+=6 {// i+2 正好是 "6K +1/-1" 中的一个值if n % i == 0 || n%(i+2) == 0 {return false}}return true
}
题目:埃氏筛
题目链接:LeetCode-204. 计数质数

思路分析:埃氏筛法思想,逐步排除掉不是质数的数
如果 x 是质数,那么大于 x 的 x 的倍数 2x,3x,… 一定不是质数。
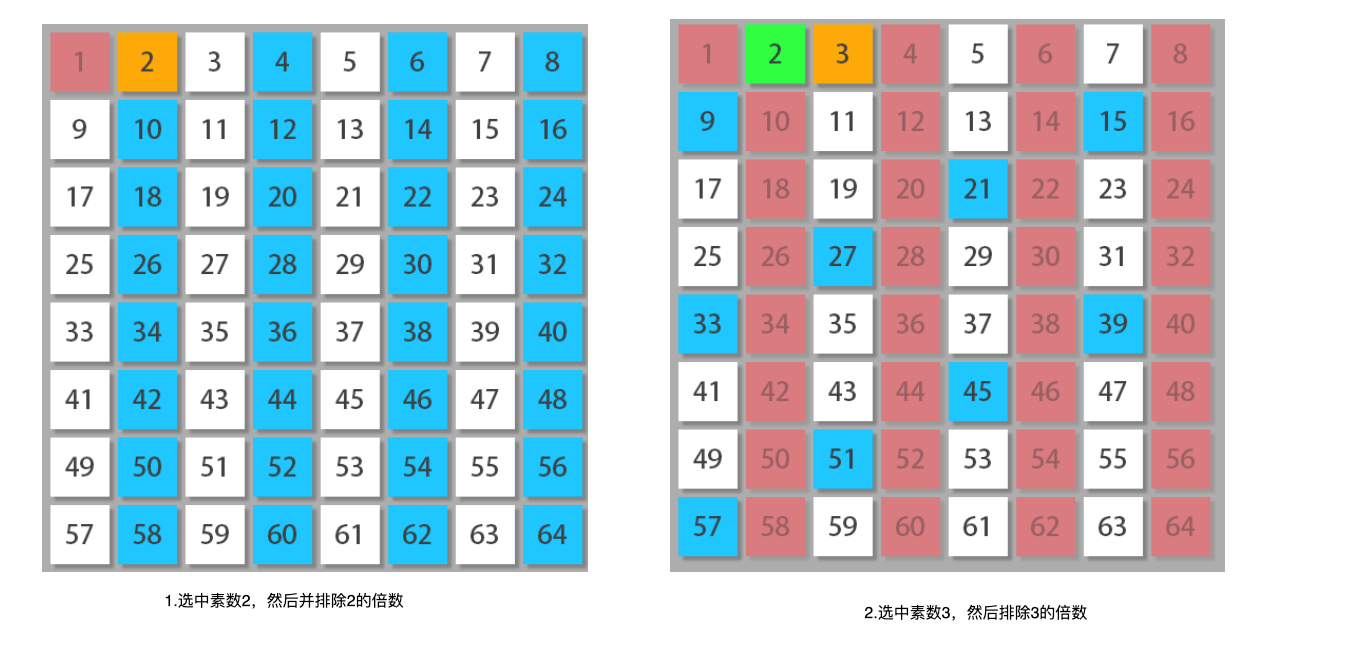
复杂度:时间复杂度 O ( n l o g l o g n ) O(n log log n) O(nloglogn)、空间复杂度 O ( n ) O(n) O(n)
- 时间复杂度分析:
- 外层循环的迭代次数是 n-2,即 O ( n ) O(n) O(n) 次。
- 内层循环的迭代次数是在素数的情况下,从 i*i 开始,每次递增 i,直到 n。这是因为小于 i 的倍数在之前已经被标记为非质数。内层循环迭代次数约为 n/i,其中 i 为质数。因此,总的迭代次数为 n/2 + n/3 + n/5 + …,这个和式是 O ( n l o g l o g n ) O(n log log n) O(nloglogn)的。
Go代码
func countPrimes(n int) int {count := 0isNotPrimes := make([]bool, n)for i:=2; i<n; i++ {if !isNotPrimes[i] {count++for j:=i*i; j<n; j+=i {isNotPrimes[j] = true}}}return count
}
或者 下面这个语言更清晰,不过多了 O ( n ) O(n) O(n)的时间复杂度
func countPrimes(n int) (count int) {isPrimies := make([]bool, n)for i, _ := range isPrimies {isPrimies[i] = true}for i:=2; i<n; i++ {// 从2开始已经把2的所有倍数标记为false,3也是,所以剩下的未标记的都是质数if isPrimies[i] {count++// 直接从i*i开始标记,因为2i,3i...这些数一定在i之前就被其他数的倍数标记过了,例如2的所有倍数,3的所有倍数等for j:=i*i; j<n; j+=i {isPrimies[j] = false}}}return
}
题目:判断是不是丑数
题目链接:LeetCode-263. 丑数

思路分析:循环除2 3 5 判断最后值是否==1
复杂度:时间复杂度 O ( l o g n ) O(log n) O(logn)、空间复杂度 O ( 1 ) O(1) O(1)
- 时间复杂度:取决于对n除以2 3 5的次数,由于每次至少将n除以2,所以除法运算的次数不会超过 O ( l o g n ) O(log n) O(logn)
Go代码
func isUgly(n int) bool {if n < 1 {return false}if n == 1 {return true}arr := [3]int{2,3,5}for _, v := range arr {for n%v == 0 {n = n/v}}return n == 1
}
相关文章:

[Go版]算法通关村第十三关黄金——数字数学问题之数论问题(最大公约数、素数、埃氏筛、丑数)
目录 题目:辗转相除法(求最大公约数)思路分析:辗转相除法(也叫欧几里得算法)gcd(a,b) gcd(b,a mod b)复杂度:时间复杂度 O ( n l o g ( m a x ) ) O(nlog(max)) O(nlog(max))、空间复杂度 O (…...
Qt双击某一文件通过自己实现的程序打开,并加载文件显示
双击启动 简述方法一方法二注意 简述 在Windows系统中,双击某类扩展名的文件,通过自己实现的程序打开文件,并正确加载及显示文件。有两种方式可以到达这个目的。 对于系统不知道的扩展名的文件,第一次打开时,需要自行…...

硬件产品的量产问题------硬件工程师在产线关注什么
前言: 产品开发测试无误,但量产缺遇到很多不良甚至DOA问题。 硬件开发过程中如何确保产线的治具、生产及硬件工程师在产线需要关注一些什么。 坚信:好的产品是要可以做出来的。 1、禁忌: 禁忌热插拔;禁忌测试不防呆…...
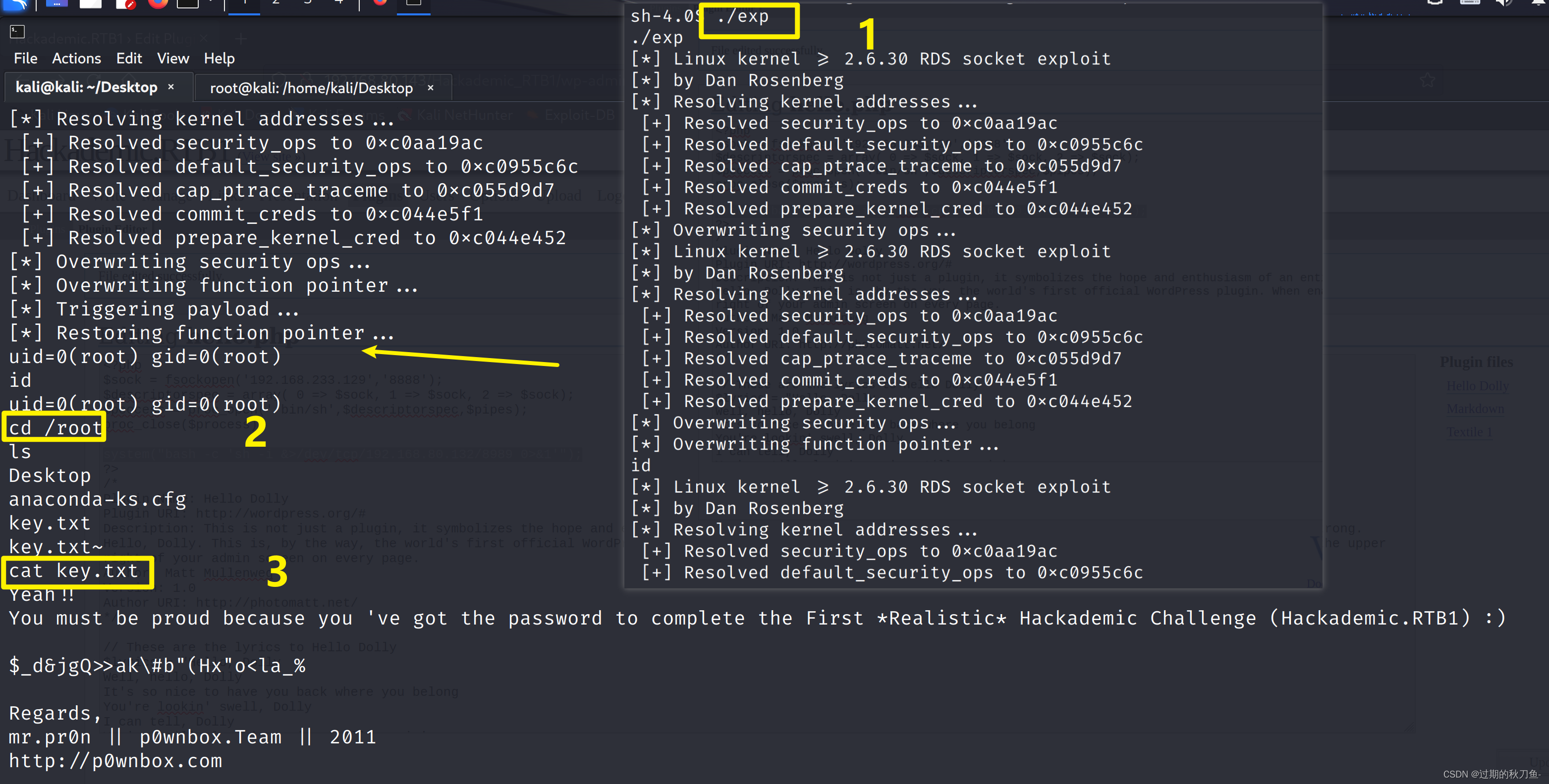
Vulnhub系列靶机--- Hackadmeic.RTB1
系列:Hackademic(此系列共2台) 难度:初级 信息收集 主机发现 netdiscover -r 192.168.80.0/24端口扫描 nmap -A -p- 192.168.80.143访问80端口 使用指纹识别插件查看是WordPress 根据首页显示的内容,点击target 点击…...
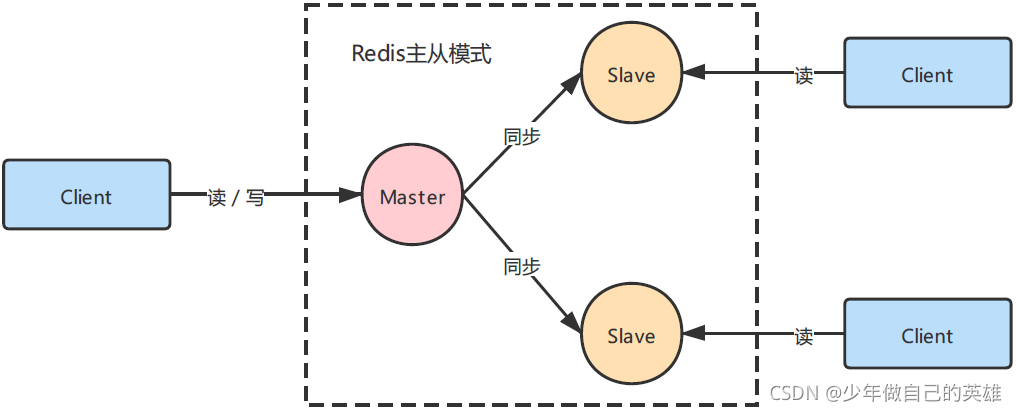
redis高级----------主从复制
redis的四种模式:单例模式;主从模式;哨兵模式,集群模式 一、主从模式 单例模式虽然操作简单,但是不具备高可用 缺点: 单点的宕机引来的服务的灾难、数据丢失单点服务器内存瓶颈,无法无限纵向扩…...

posgresql通过PL/pgSQL脚本统一修改某字段大小写
项目在做postgresql数据库适配时遇到了某些问题,需要统一将某个模式含id字段的全部表,将id字段由小写转换为大写,可以通过PL/pgSQL脚本实现。 先确保当前用户有足够的权限 DO $$ DECLARE current_table text;current_column text; BEGIN --…...

iPhone卫星通信SOS功能如何在灾难中拯救生命
iPhone上的卫星紧急求救信号功能在从毛伊岛野火中拯救一家人方面发挥了至关重要的作用。这是越来越多的事件的一部分,在这些事件中,iPhone正在帮助人们摆脱危及生命的情况。 卫星提供商国际通信卫星组织负责移动的高级副总裁Mark Rasmussen在接受Lifewir…...

NOIP真题答案 过河 数的划分
过河 题目描述 在河上有一座独木桥,一只青蛙想沿着独木桥从河的一侧跳到另一侧。在桥上有一些石子,青蛙很讨厌踩在这些石子上。由于桥的长度和青蛙一次跳过的距离都是正整数,我们可以把独木桥上青蛙可能到达的点看成数轴上的一串整点…...
图为科技-边缘计算在智慧医疗领域的作用
边缘计算在智慧医疗领域的作用 随着科技的进步,智慧医疗已成为医疗行业的重要发展趋势。边缘计算作为新兴技术,在智慧医疗领域发挥着越来越重要的作用。本文将介绍边缘计算在智慧医疗领域的应用及其优势,并探讨未来发展方向。 一、边缘计算…...
Linux配置nginx反向代理
在云服务器上部署高并发的服务,使用Nginx作为反向代理是一种常见的做法,可以实现流量分发、负载均衡,同时提升系统的可靠性和性能。 步骤概览: 安装Nginx: 确保服务器已安装Nginx。若未安装,可使用适用于你…...

随便记录记录
统一整理一下各种 pandas读csv import pandas as pd ## 默认会将第一行作为列 df pd.read_csv(path_to_your_file.csv) ## 传递 headerNone 参数来告诉 Pandas 不要将第一行 df pd.read_csv(path_to_your_file.csv, headerNone) ## 使用多种选项来处理数据,如指…...

UbuntuDDE 23.04发布,体验DeepinV23的一个新选择
UbuntuDDE 23.04发布,体验DeepinV23的一个新选择 昨晚网上搜索了一圈,无意看到邮箱一条新闻,UbuntuDDE 23.04发布了 因为前几天刚用虚拟机安装过,所以麻溜的从网站下载了ISO文件,安装上看看。本来没多想,…...
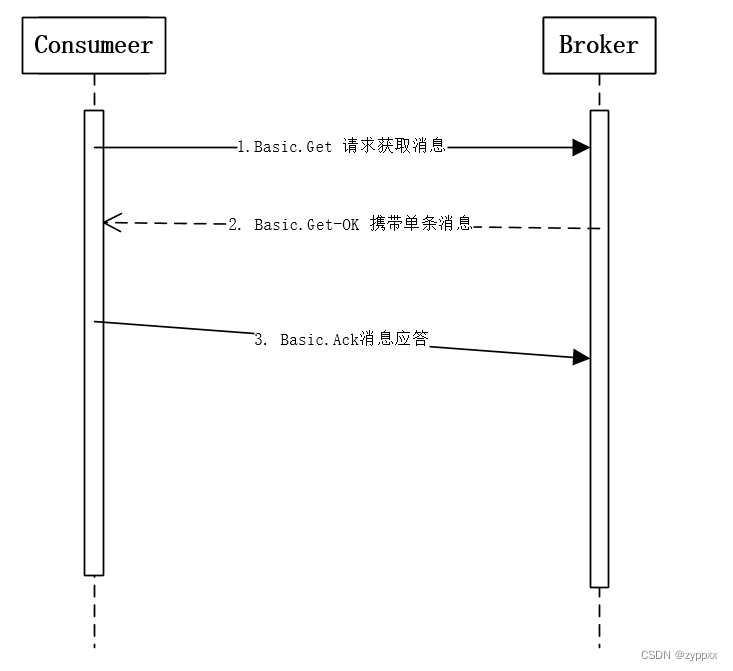
RabbitMQ 消费者
RabbitMQ的消费模式分两种:推模式和拉模式,推模式采用Basic.Consume进行消费,拉模式则是调用Basic.Get进行消费。 消费者通过订阅队列从RabbitMQ中获取消息进行消费,为避免消息丢失可采用消费确认机制 消费者 拉模式拉模式的实…...

软件测试面试真题 | 什么是PO设计模式?
面试官问:UI自动化测试中有使用过设计模式吗?了解什么是PO设计模式吗? 考察点 《page object 设计模式》:PageObject设计模式的设计思想、设计原则 《web自动化测试实战》:结合PageObject在真实项目中的实践与应用情…...

GB2312转UTF-8部分中文乱码
现象 最近写了个txt导入,客户反馈有时候导入的数据,会出现个别中文乱码的现象,但是我之前已经做过编码转换处理了,统一转成了UTF-8。 比如“鞠婧祎”,导入进来是这样: 排查思路 首先看了一下这个文本的编码格式&am…...
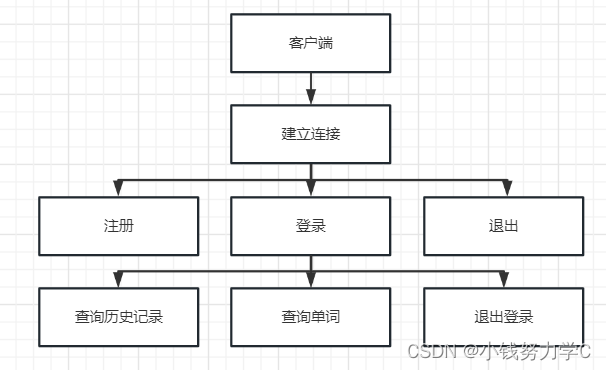
项目——电子词典(客户端、服务器交互,字典导入,单词查询)
一、项目要求 登录注册功能,不能重复登录,重复注册单词查询功能历史记录功能,存储单词,意思,以及查询时间基于TCP,支持多客户端连接采用数据库保存用户信息与历史记录将dict.txt的数据导入到数据库中保存。…...
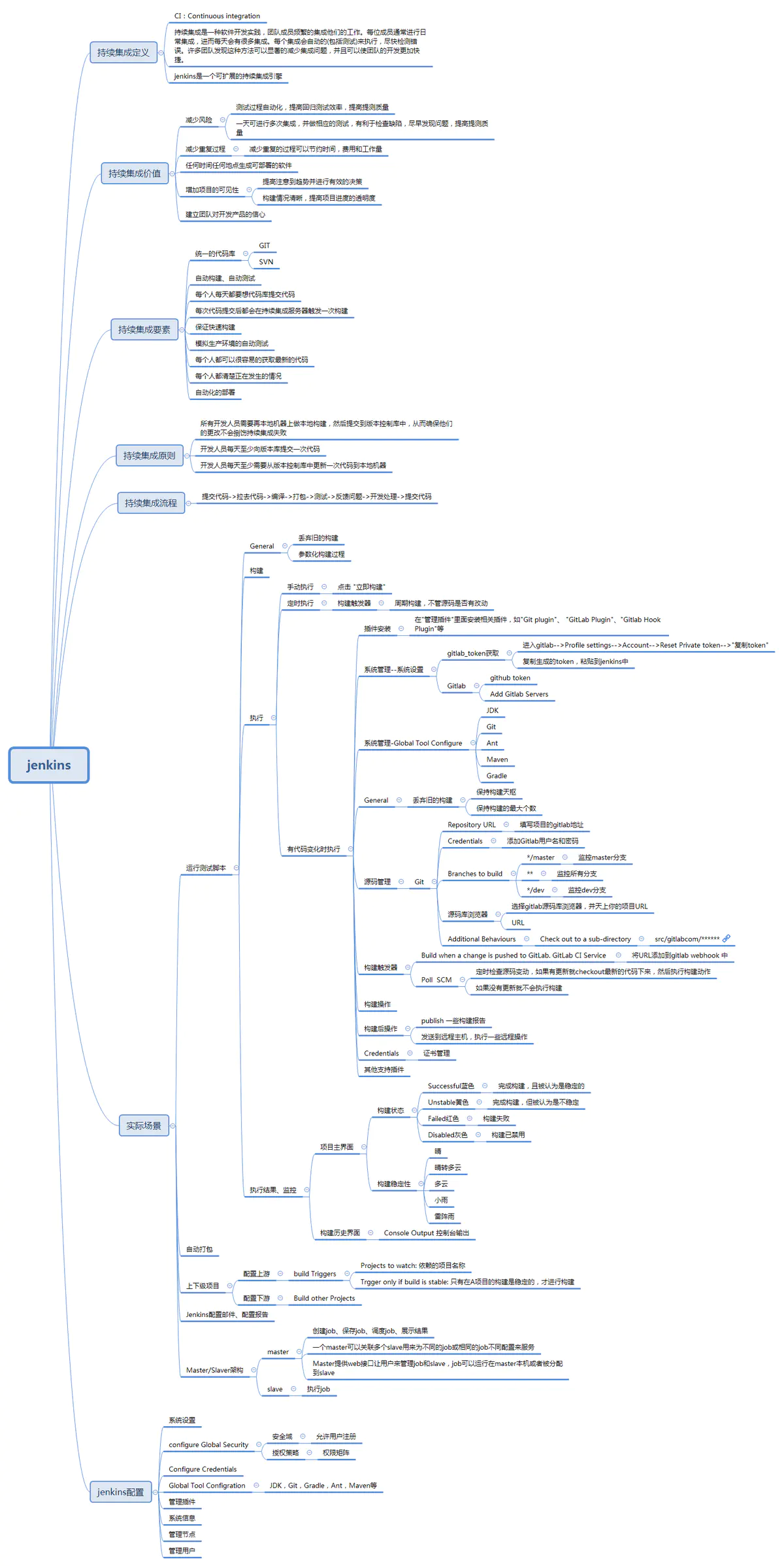
jenkins 是什么?
一、jenkins 是什么? Jenkins是一个开源的、提供友好操作界面的持续集成(CI)工具,起源于Hudson,主要用于持续、自动的构建/测试软件项目、监控外部任务的运行。Jenkins用Java语言编写,可在Tomcat等流行的servlet容器中运行&#…...

无涯教程-PHP - sql_regcase()函数
sql_regcase() - 语法 string sql_regcase (string string) 可以将sql_regcase()函数视为实用程序函数,它将输入参数字符串中的每个字符转换为包含两个字符的带括号的表达式。 sql_regcase() - 返回值 返回带括号的表达式字符串以及转换后的字符。 sql_regcase…...

cesium 实现鼠标中键拖动地图
cesium默认左键拖动地图,中键旋转,再绘图时带来诸多不便。所以改成鼠标中键按下拖动地图,鼠标左键选点。代码如下:【感谢chatGPT】 //改为中建拖动// 假设 viewer 是你的 Cesium Viewer 实例const cameraController viewer.scene…...

低压风机单片机方案
低压风机通常由电机、转子、机壳、进气管、出气管、齿轮和减速机等组成。电机带动转子旋转,旋转的转子带动齿轮和减速机转动,进而形成空气被吸入转子内部,通过旋转而产生的离心力把气体压缩,并将气体排出。 低压风机方案的主控型…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...
