二叉树、红黑树、B树、B+树
二叉树
一棵二叉树是结点的一个有限集合,该集合或者为空,或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
二叉树的特点:
- 每个结点最多有两棵子树,即二叉树不存在度大于2的结点。
- 二叉树的子树有左右之分,其子树的次序不能颠倒。
满二叉树
满二叉树:二叉树的所有叶子节点都在最后一层且总数n=2^(n-1)。

完全二叉树
完全二叉树:数据从上到下,从左到右依次进行平铺。
有序二叉树
有序二叉树:左子树上的值小于根节点的值,右子树上的值大于根节点的值。
有序二叉树的遍历:
深度优先遍历:
1、先序/前序遍历:根节点----》左子树-----》右子树
2、中序遍历:左子树----》根节点-----》右子树
3、后序遍历:左子树----》右子树-----》根节点
有序二叉树不稳定:O(logn) - O(n)
有序二叉树不稳定是因为没有任何限制,以至于在某些特殊的情况下会形成链表。
平衡二叉树
平衡二叉树是在有序二叉树的基础之上而来的,就是为了解决有序二叉树不稳定的问题。要求:一个节点的左右子树高度差的绝对值不能超过1,可以等于1。
如果插入的数据之后使得一个节点的左右子树高度差的绝对值超过了1,就要通过LL、RR、LR、RL四种旋转策略来保证平衡二叉树。
四种旋转策略
LL旋转策略:

实例:

RR旋转策略:

实例:

LR旋转策略:

实例:

RL旋转策略:

实例:
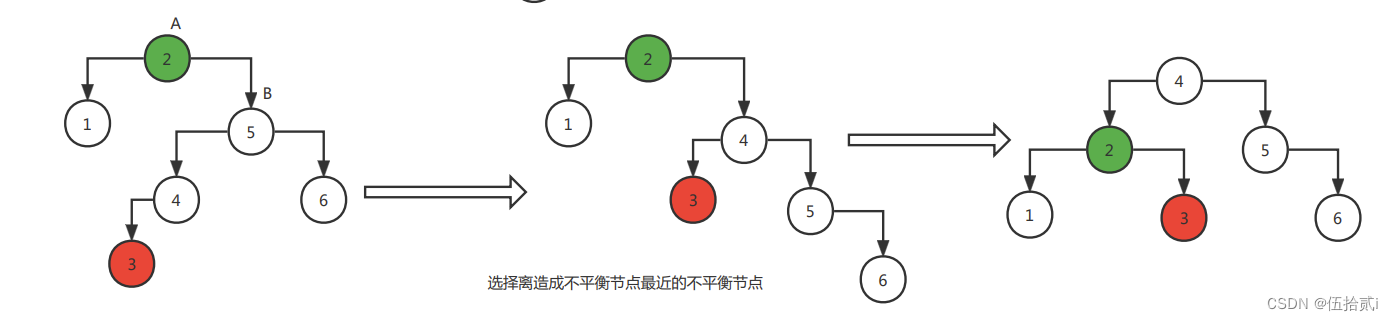
在实行旋转策略是,选择距离造成不平衡节点最近的不平衡节点作为要操作节点。
平衡二叉树特别稳定,但每次进行调整都会耗费计算机性能。
我们想既要时间复杂度在O(logn),又要十分稳定,还要不耗费计算机性能,这时,推出了红黑树。
红黑树(基于2-3-4树)
2-3-4树是从下向上构建的。节点内升序,每个节点最多有3个值,当插入第4个值时,需要在这四个之中选中间值进行升元。
实例:

然后通过2-3-4树转换 形成红黑树
转换规则如下图:

将刚刚的2-3-4树转换为红黑树:

红黑树的特点:
1、红黑树中每一个节点不是红色节点就是黑色节点。
2、红黑树当中根节点一定是黑色的。———>在转化的过程中2-3-4节点都是以黑色节点开头的
3、每一个叶子节点都是黑色的。
4、从根节点到任意一个叶子节点的路径上所走过的黑色节点的数量相同
5、如果一个节点是红色的,那么他的子节点一定是黑色
4、5条特点会导致最长的路径绝对不会超过最短路径的2倍。例如最长路径为黑红黑红黑红,最短路径为黑黑黑。
为什么红黑树是O(logn)?
2-3-4树是多叉树,如果数据相等,它的时间复杂度小于传统二叉树,2-3-4树的时间复杂度
红黑树最复杂的时候也就是变为2倍,变为2logn。这是依旧可以看成是logn。
B树
多叉树以B树为最基本点。2-3-4树来源于B树。
B树特点:
1、B树的数据存储是 key-value类型的。
2、B树有几个叉:并不确定,要看具体实现。
3、M阶B树
3.1、每个节点上最多有 M-1 个值,并且以升序排列。3阶B树每个节点最多有两个值。.....(2-3-4树属于4阶B树)
红黑树和B树如果都在内存中,内存向cpu提供数据的时间相等,由于红黑树对比次数相对较少,所以红黑树是内存最优二叉树。
为什么要有B树:
红黑树和B树如果都在磁盘中--------》数据寻址浪费时间--------》磁头移动的物理时间+平均盘面旋转半圈
B树多用于磁盘,原因是分出多个叉,降低树的高度,降低寻址次数和时间。
B树优胜于寻址,但是数据进行对比还是要在内存中。
B+树
在B树基础上改造出现的B+树,但和传统B树又不太一样。B+树是mysql数据库专用底层数据结构。
B+树的特点:
1、非叶子节点仅具有索引功能,也就是说非叶子节点只能存储key值,不能存储value值。
2、B+树的所有叶子节点会构成一个有序的链表,这样就可以根据key值遍历数据。
之所以有这两个特点就是为数据库的功能服务
B+树的构建

插入 3 ,4

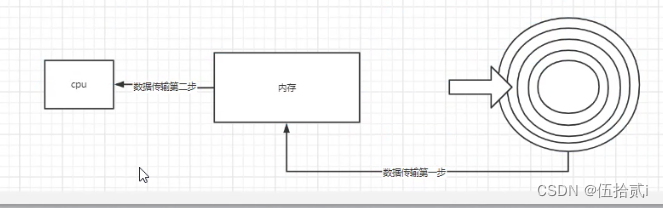
磁盘向cpu推送数据:每次需要推送一页(4kb)的数据,如两个文件 2kb+3kb,只能先推送2kb,再推送3kb。
B+树的优点:
1、非叶子节点不包含数据,只能放索引,这样每次就可以向内存当中传输更多的key值,在内存当中进行数据比对,在磁盘当中进行数据查询。
2、叶子节点是链接在一起的,这样有利于区间查询。
相关文章:

二叉树、红黑树、B树、B+树
二叉树 一棵二叉树是结点的一个有限集合,该集合或者为空,或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。 二叉树的特点: 每个结点最多有两棵子树,即二叉树不存在度大于2的结点。二叉树的子树有左右之分…...

12,【设计模式】工厂
设计模式工厂 通过工程来构建任意参数对象&&std::forwardstd::move 在C中,“工厂”(Factory)是一种设计模式,它提供了一种创建对象的方式,将对象的创建和使用代码分离开来,提高了代码的可扩展性和可…...
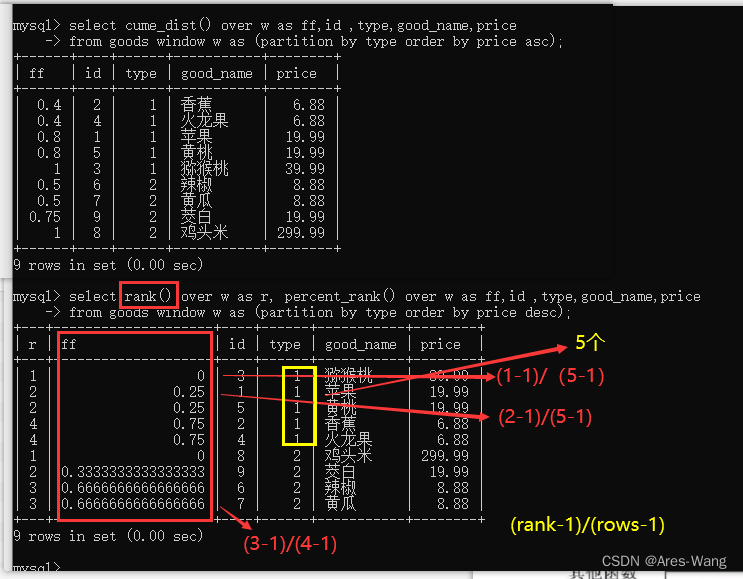
mysql 8.0 窗口函数 之 分布函数 与 sql server (2017以后支持) 分布函数 一样
mysql 分布函数 percent_rank() :等级值 百分比cume_dist() :累积分布值 percent_rank() 计算方式 (rank-1)/(rows-1), 其中 rank 的值为使用RANK()函数产生的序号,rows 的值为当前…...

Python Opencv实践 - 图像直方图自适应均衡化
import cv2 as cv import numpy as np import matplotlib.pyplot as pltimg cv.imread("../SampleImages/cat.jpg", cv.IMREAD_GRAYSCALE) print(img.shape)#整幅图像做普通的直方图均衡化 img_hist_equalized cv.equalizeHist(img)#图像直方图自适应均衡化 #1. 创…...

Linux编程:在程序中异步的调用其他程序
Linux编程:execv在程序中同步调用其他程序_风静如云的博客-CSDN博客 介绍了同步的调用其他程序的方法。 有的时候我们需要异步的调用其他程序,也就是不用等待其他程序的执行结果,尤其是如果其他程序是作为守护进程运行的,也无法等待其运行的结果。 //ssss程序 #include …...

04有监督算法——支持向量机
1.支持向量机 1.1 定义 支持向量机( Support Vector Machine )要解决的问题 什么样的法策边界才是最好的呢? 特征数据本身如果就很难分,怎么办呢? 计算复杂度怎么样?能实际应用吗? 支持向量机( Support Vector Machine , SVM)是一类按监督学习( s…...
)
macos 使用vscode 开发python 爬虫(安装一)
使用VS Code进行Python爬虫开发是一种常见的选择,下面是一些步骤和建议: 安装VS Code:首先,确保你已经在你的macOS上安装了VS Code。你可以从官方网站(https://code.visualstudio.com/)下载并安装最新版本…...

专有网络VPC私网/公网类产品选择
私网类产品选择 VPC互连:云企业网,对等连接 VPC与本地IDC互连:VPN网关,高速通道,云企业网,智能接入网关 VPC与多站点连接:VPN网关,智能接入网关,VPN网关高速通道 远程接…...
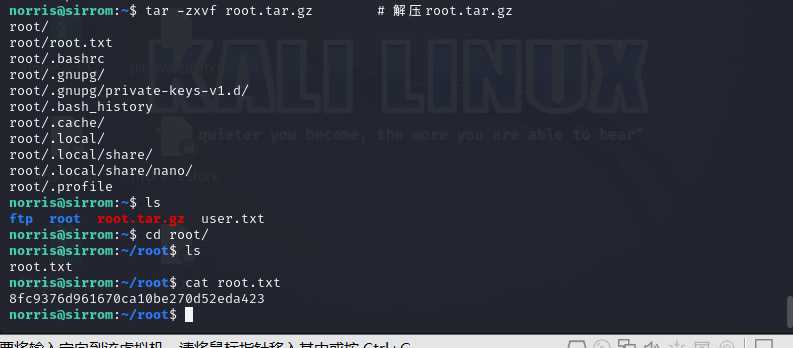
Connect-The-Dots靶场
靶场下载 https://www.vulnhub.com/entry/connect-the-dots-1,384/ 一、信息收集 探测存活主机 netdiscover -r 192.168.16.161/24nmap -sP 192.168.16.161/24端口操作系统扫描 nmap -sV -sC -A -p 1-65535 192.168.16.159扫描发现开放端口有 21 ftp 80 http 20…...

Linux解决RocketMQ中NameServer启动问题
启动步骤可以查看官网,https://github.com/apache/rocketmq 一下说明遇到的问题。 1:ROCKETMQ_HOME问题 根据官网提示进入mq/bin目录下,可以使用./mqnamesrv进行NameServer启动,但是会遇到第一个问题,首次下载Rocket…...
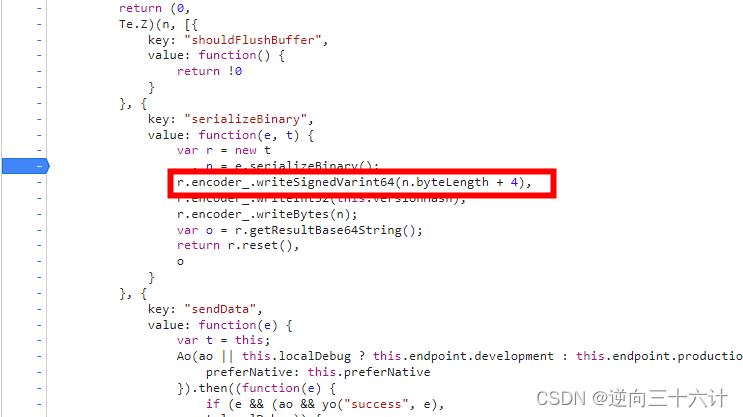
js逆向实战之某书protobuf反序列化
什么是Protobuf? \qquad Protobuf(Protocol Buffer)是 Google 开发的一套数据存储传输协议,作用就是将数据进行序列化后再传输,Protobuf 编码是二进制的,它不是可读的,也不容易手动修改…...
cpolar+JuiceSSH实现手机端远程连接Linux服务器
文章目录 1. Linux安装cpolar2. 创建公网SSH连接地址3. JuiceSSH公网远程连接4. 固定连接SSH公网地址5. SSH固定地址连接测试 处于内网的虚拟机如何被外网访问呢?如何手机就能访问虚拟机呢? cpolarJuiceSSH 实现手机端远程连接Linux虚拟机(内网穿透,手机端连接Linux虚拟机) …...
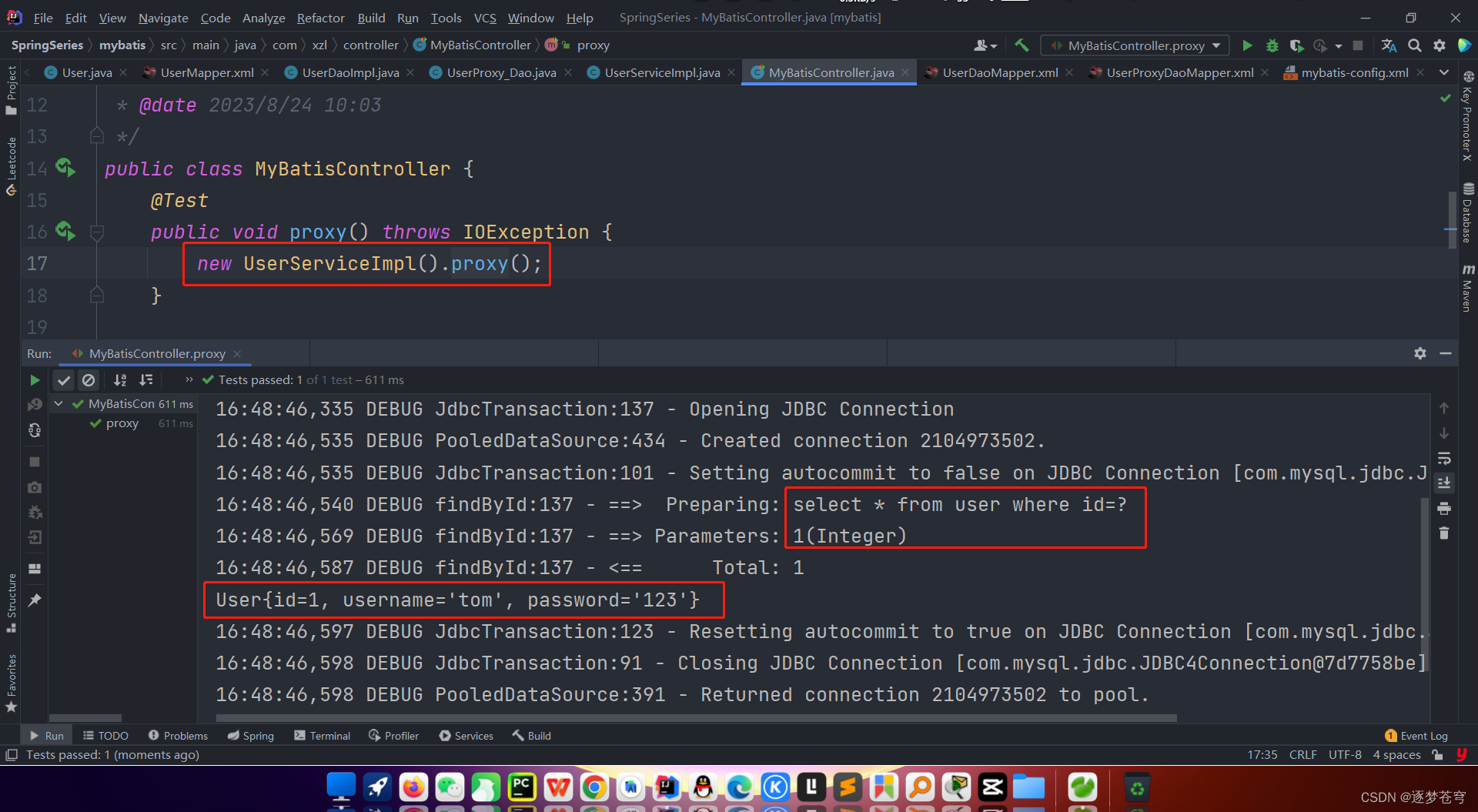
[MyBatis系列②]Dao层开发的两种方式
目录 1、传统开发 1.1、代码 1.2、存在的问题 2、代理开发 2.1、开发规范 2.2、代码 ⭐mybatis系列①:增删改查 1、传统开发 传统的mybatis开发中,是在数据访问层实现相应的接口,在实现类中用"命名空间.id"的形式找到对应的映…...

言语理解-中心理解之主题词及行文脉络
例题 例题 例题 例题 例题 例题...

LeetCode 面试题 01.05. 一次编辑
文章目录 一、题目二、C# 题解法一:从第一个不同位置处判断后续相同子串法二:前后序遍历判断第一个不同字符的位置关系 优化法一法二 一、题目 字符串有三种编辑操作:插入一个英文字符、删除一个英文字符或者替换一个英文字符。 给定两个字符串ÿ…...

Mybatis查询in的字段过多不走索引
mybatis查询in的字段有索引,比如说是主键查询, 但是in的字段过多导致索引失效, 这个时候可以考虑将in的数量变少, 200以内都可以, 在数据库方面采用 foreach unionall 的方式将数据集合查询出来 Service层: List<…...
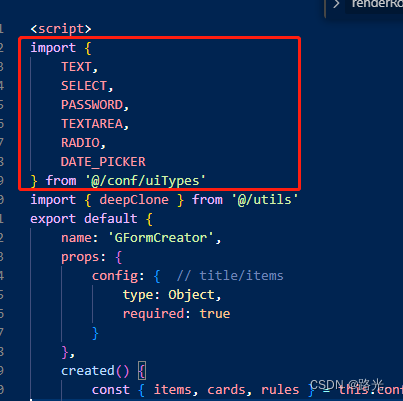
封装公共el-form表单(记录)
1.公共表单组件 //commonForm.vue <script> import {TEXT,SELECT,PASSWORD,TEXTAREA,RADIO,DATE_PICKER } from /conf/uiTypes import { deepClone } from /utils export default {name: GFormCreator,props: {config: { // title/itemstype: Object,required: true}}…...

List 分批处理
1.Google Guava <dependency><groupId>com.google.guava</groupId><artifactId>guava</artifactId><version>31.0.1-jre</version></dependency>List<String> tempList Arrays.asList("水星","金星&qu…...

SpringSession
Spring Session 是 Spring 的项目之一。Spring Session 提供了一套创建和管理 Servlet HttpSession 的方案,默认采用外置的 Redis 来存储 Session 数据,以此来解决 Session 共享的 问题。(springsession储存session数据的方式有很多,我们常…...

Python Web 开发之 JWT 简介
在之前的课程中,介绍过 Flask-Login 框架,它是基于 Session 和 Cookie 技术来实现用户授权和验证的,不过 Session 有很多的局限性,这一节介绍一种基于 token 的验证方式 —— JWT (JSON Web Token),除了对 JWT 的概念讲解之外&…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
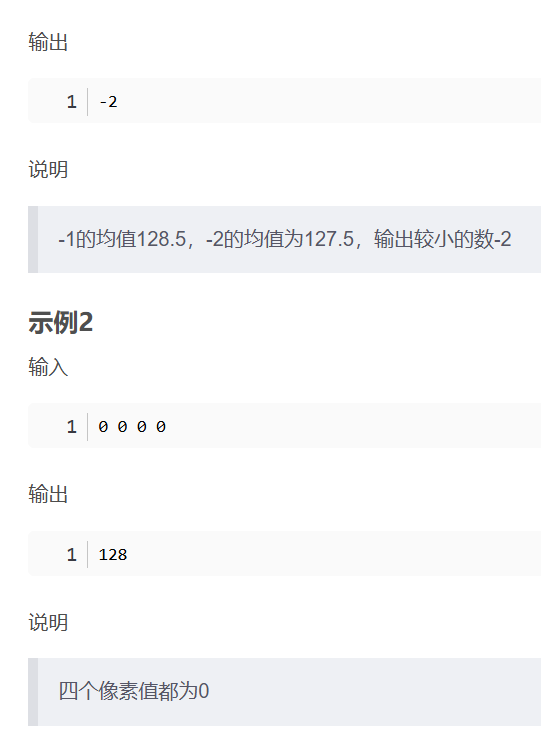
华为OD机考- 简单的自动曝光/平均像素
import java.util.Arrays; import java.util.Scanner;public class DemoTest4 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint[] arr Array…...
