Dynaminc Programming相关
目录
3.1 最长回文子串(中等):标志位
3.2 最大子数组和(中等):动态规划
3.3 爬楼梯(简单):动态规划
3.4 买卖股票的最佳时机(简单):动态规划
3.5 买卖股票的最佳时机Ⅱ(中等):动态规划
3.6 生成括号(中等):递归
3.7 打家劫舍(中等):动态规划
3.8 跳跃游戏(中等):贪心算法
3.9 最长递增子序列(中等):动态规划
3.10 不同路径(中等):动态规划
3.11 零钱兑换(中等):动态规划
3.12 最小路径和(中等):动态规划
3.13 动态规划总结!!!
3.1 最长回文子串(中等):标志位
题目:给你一个字符串 s,找到 s 中最长的回文子串。如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。
思想:假设回文子串的左右边界开始为0,长度为1(已经对s=0或者s=1进行了判断),创建一个二维boolean数组,长度为均s的长度,分别从s的左右边界遍历,当值相等时判断此时的左右边界内部:
-
若内部只有一个元素,此时就是一个回文子串,然后将这部分字符串设置为true
-
若内部也是一个回文字符串,则左右边界和内部共同为一个字符串
-
设置为true后计算此时的回文子串长度是否大于开始设定的回文子串长度1,若大于就修改回文子串长度
-
返回s的
substring即可
-
总结:利用巧妙的标志位来处理回文子串的内部情况
代码:
class Solution {
public String longestPalindrome(String s) {if (s == null || s.length() < 2) {return s;}int strLen = s.length();int maxStart = 0; //最长回文串的起点int maxEnd = 0; //最长回文串的终点int maxLen = 1; //最长回文串的长度
boolean[][] dp = new boolean[strLen][strLen];
for (int r = 1; r < strLen; r++) {for (int l = 0; l < r; l++) {if (s.charAt(l) == s.charAt(r) && (r - l <= 2 || dp[l + 1][r - 1])) {dp[l][r] = true;if (r - l + 1 > maxLen) {maxLen = r - l + 1;maxStart = l;maxEnd = r;}}}}return s.substring(maxStart, maxEnd + 1);}
}3.2 最大子数组和(中等):动态规划
题目:给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。子数组 是数组中的一个连续部分。
思想:设f(i)表示第i位的最大连续子数组,将f(i)存入F,则我们只需要将F中最大的f(i)取出即可
-
f(i)的值和f(i-1)有关,若f(i-1)+ 当前nums[i]值还小于f(i),则说明nums[i]就是当前最大的连续子数组f(i)-
即:
f(i) = max{f(i - 1) + nums[i], nums[i]}
-
总结:用一个prev每次存储f(i)的值,然后和之前的最大子数组和相比较
代码:
class Solution {public int maxSubArray(int[] nums) {//设置一个prev,用来记录f(i-1)int prev = 0;//最大连续子数组,第一个f(i)就是数组的第一个值int maxArray = nums[0];
//遍历数组for(int curr : nums){//求出当前的f(i),当前的f(i)就是下一次遍历的f(i - 1)prev = Math.max(prev + curr, curr);
//求f(i) 和 f(i - 1)中较大的一个maxArray = Math.max(maxArray, prev);}
return maxArray;}
}3.3 爬楼梯(简单):动态规划
题目:假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
思想:对于爬楼梯问题而言,如果:
-
第一节楼梯
f(1),只有一种方法 -
第二节楼梯
f(2),只有两种方法 -
更高阶楼梯
f(n),-
只有从
n-1上爬一阶(这是第一种方案),方案数一共为f(n-1) -
或者从
n-2上爬两阶(这是第二种方案),方案数一共为f(n-2)-
总的方案数
f(n)= 第一种方案数f(n-1)+ 第二种方案数f(n-2)
-
-
总结:利用斐波那契数列解决该问题即可;数列的定义可以表示为:F(0) = 0,F(1) = 1,F(n) = F(n-1) + F(n-2),其中 n 表示数列的索引。
代码:
class Solution {public int climbStairs(int n) {if(n < 2){return n;}int[] res = new int[n];//爬一节楼梯只有一种方法res[0] = 1;//爬两阶楼梯有两种方法res[1] = 2;//之后的每阶楼梯总的方案数f(n) = 第一种方案数 f(n-1)+ 第二种方案数f(n-2)for(int i = 2; i < n; i++){res[i] = res[i - 1] + res[i - 2];}return res[n - 1];}
}3.4 买卖股票的最佳时机(简单):动态规划
题目:给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
思想:先遍历一次数组,找到最小值prices[min],这就是股票买入的最低值,我们只需得到从该最低值min索引之后,股票差价prices[i] - preices[min] 最大的那天i,然后输出最大利润即可
总结:先找到最低股票价格(可以先设置一个minprice,因为后面会有交换操作,因此一开始给minprice赋值为正无穷),然后遍历求出股票差价,返回最大的股票差价
代码:
class Solution {public int maxProfit(int[] prices) {//设置股票最低价格和最大利润int minprice = Integer.MAX_VALUE;int maxprofit = 0;//遍历数组,求出最低价格和最大利润for(int i = 0; i < prices.length; i++){//求出最低价格if(prices[i] < minprice){minprice = prices[i];}//求出最大利润else if(prices[i] - minprice > maxprofit){maxprofit = prices[i] - minprice;}}return maxprofit;}
}3.5 买卖股票的最佳时机Ⅱ(中等):动态规划
题目:给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。返回 你能获得的 最大 利润 。
思想:
-
由于不限制是否能够在每一天都买入/卖出股票,因此我们能够获得的最大利润就是每次卖出都能获得利润的和
-
因此需要先比较卖出价值是否大于买入价值,大于就将其累加,遍历完
prices数组得到的累加值就是最大利润
-
总结:先找到最低股票价格(可以先设置一个minprice,因为后面会有交换操作,因此一开始给minprice赋值为正无穷),然后遍历求出股票差价,返回最大的股票差价
代码:
class Solution {public int maxProfit(int[] prices) {//特殊情况if(prices == null || prices.length <= 1){return 0;}
//获得利润:就必须卖出比买入大//获得的最大利润:每一次卖出都比买入大int maxprofit = 0;for(int i = 1; i < prices.length; i++){if(prices[i] > prices[i - 1]){maxprofit += prices[i] - prices[i - 1];}}return maxprofit;}
}3.6 生成括号(中等):递归
题目:数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合
思想:
-
生成所有可能的括号序列:使用递归实现:长度为
n的序列,就是在长度为n-1的序列前加了一个(或者) -
保证括号序列有效:遍历这个序列,使用变量
balance表示左括号减去右括号的数量:-
遍历过程中
balance小于0,说明)出现在(之前,此时不是有效括号 -
遍历结束时不为零,说明
(与)的个数不相等,也不是有效括号
-
总结:先找到最低股票价格(可以先设置一个minprice,因为后面会有交换操作,因此一开始给minprice赋值为正无穷),然后遍历求出股票差价,返回最大的股票差价
代码:
class Solution {public List<String> generateParenthesis(int n) {//存储括号组合的数组List<String> res = new ArrayList<>();
//调用方法:该方法能够生成所有可能的括号组合,并将其保存到res中generateAll(res, new char[2 * n], 0);return res;}
//生成所有可能的括号组合public void generateAll(List<String> res, char[] curr, int pos){if(pos == curr.length){if(isValid(curr)){res.add(new String(curr));}}else{curr[pos] = '(';generateAll(res,curr,pos + 1);curr[pos] = ')';generateAll(res,curr,pos + 1);}}
//判断是否为有效括号组合:根据balance判断,若为'('则balance + 1;若为')'则balance - 1//上式只能判断 '(' 与 ')'个数是否相等,无法判断是否有效//先对'('进行balance++,记录'('的个数,倘若balance < 0,则说明 ')' 出现在 '('之前,此时不是有效括号public boolean isValid(char[] curr){//记录左右括号之差的变量int balance = 0;
for(char c : curr){if(c == '('){balance++;}else{balance--;}if(balance < 0){return false;}}return balance == 0;}
}3.7 打家劫舍(中等):动态规划
题目:你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
思想:
-
没有房屋:偷窃最高金额为0
-
只有一间房屋:偷窃最高金额就是数组值(当前房屋值)
-
只有两间房屋:偷窃最高金额是这两件房屋中金额较多的一个
-
房屋数
k > 2时,偷窃最高金额有两种选择:-
若偷窃第
k家,则f(k) = num[k] + f(k - 2)(偷窃第 k间房屋,那么就不能偷窃第 k−1 间房屋,偷窃总金额为前 k−2 间房屋的最高总金额与第 k的金额之和) -
若不偷窃第
k家,则f(k) = f(k - 1)(不偷窃第 k间房屋,偷窃总金额为前 k−1间房屋的最高总金额)
-
总结:先找到最低股票价格(可以先设置一个minprice,因为后面会有交换操作,因此一开始给minprice赋值为正无穷),然后遍历求出股票差价,返回最大的股票差价
代码:
class Solution {public int rob(int[] nums) {int len = nums.length;
//没有房屋返回0if(nums == null || len == 0){return 0;}//只有一间房屋返回当前值else if(len == 1){return nums[0];}//两间房比较大小返回较大的一个else if(len == 2){return Math.max(nums[0], nums[1]);}//超过三间房返回两者中较大的一个int[] maxRob = new int[len];maxRob[0] = nums[0];maxRob[1] = Math.max(nums[0],nums[1]);for(int i = 2; i < len; i++){maxRob[i] = Math.max(nums[i] + maxRob[i-2], maxRob[i-1]);}return maxRob[len - 1];}
}3.8 跳跃游戏(中等):贪心算法
题目:给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。
思想:对于任意一个索引位置y,可达它的条件是当前位置x加上最大可达位置之和大于等于y;最大可达位置是每次的当前位置x+当前元素nums[x];我们只记录一个最大可达位置,如果进行跳跃时到达了下一个下标,该下标的最大可达位置小于之前的最大可达位置,则不更新最大可达位置
总结:需要先找到该问题的核心:如何确定能够到达最后一个下标?因此引入了最大可达位置变量,遍历数组:若可达,则判断是否需要更新最大可达位置的值,若不可达最后一个索引位置,则返回false
代码:
class Solution {public boolean canJump(int[] nums) {int len = nums.length;//设置最大可达位置int maxReachPosition = 0;
//遍历数组;当数组的索引值小于等于最大可达位置,就说明当前位置可达;//到达当前索引位置,判断是否需要更新最大可达位置for(int i = 0; i < len; i++){if(maxReachPosition >= i){maxReachPosition = Math.max(maxReachPosition, i + nums[i]);//判断最大可达位置是否大于等于最后一个索引位置,只要成立就结束方法返回trueif(maxReachPosition >= len - 1){return true;}}}return false;}
}3.9 最长递增子序列(中等):动态规划
题目:给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
思想:设置dp[i]用来表示到第i个元素时的最长递增子序列,则dp[0,...i-1]就是在dp[i]之前已经计算出的最长递增子序列:则
-
dp[i] =max(dp[j] + 1 , dp[i]), j < i && nums[j] < nums[i];因为j并不一定是i - 1,最终最长的递增子序列就是
dp[i]的最大值
总结:需要先找到该问题的核心:如何确定能够到达最后一个下标?因此引入了最大可达位置变量,遍历数组:若可达,则判断是否需要更新最大可达位置的值,若不可达最后一个索引位置,则返回false
代码:
class Solution {public int lengthOfLIS(int[] nums) {if(nums == null || nums.length == 0){return 0;}//设置数组存储每个dp[i]的最长递增子序列int[] dp = new int[nums.length];
//只有一个元素,最长递增子序列就是1dp[0] = 1;int result = 1;//dp[i] = max(dp[j]+1 , dp[i]) , j < i && nums[j] < nums[i]for(int i = 1; i < nums.length; i++){dp[i] = 1;for(int j = 0; j < i; j++){if(nums[j] < nums[i]){dp[i] = Math.max(dp[j] + 1, dp[i]);}}result = Math.max(dp[i],result);}return result;}
}3.10 不同路径(中等):动态规划
题目:一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。问总共有多少条不同的路径?
思想:设f(i,j)表示为到达(i,j)的路径数量,为了到达(i,j),可能的路径方案有两种:
-
从
(i-1,j)位置向下走一步,到达(i,j),此时的方法数为f(i-1,j) -
从
(i,j-1)位置向右走一步,到达(i,j),此时的方法数为f(i,j-1) -
故:
f(i,j) = f(i-1,j) + f(i,j-1) -
边界条件:
f(0,0)=f(0,j)=f(i,0)=1,只有一个点、只有一行、只有一列的情况路径数都只有一个
总结:需要先找到该问题的核心:如何确定能够到达最后一个下标?因此引入了最大可达位置变量,遍历数组:若可达,则判断是否需要更新最大可达位置的值,若不可达最后一个索引位置,则返回false
代码:
class Solution {public int uniquePaths(int m, int n) {//f(i,j)表示到达(i,j)的路径数,i < m, j < nint[][] res = new int[m][n];
//只有一行:路径数为1for(int i = 0; i < m; i++){res[i][0] = 1;}
//只有一列:路径数为1for(int j = 0; j < n; j++){res[0][j] = 1;}
//否则:f(i,j) = f(i-1,j) + f(i,j-1)for(int i = 1; i < m; i++){for(int j = 1; j < n; j++){res[i][j] = res[i - 1][j] + res[i][j-1];}}
//返回res到达(m,n)的值return res[m-1][n-1];}
}3.11 零钱兑换(中等):动态规划
题目:给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。你可以认为每种硬币的数量是无限的。
思想:将凑成总金额i的最少硬币数量设为f(i),假设f(0)、f(1)、f(i-1)已知,则f(i)=min(f(i-coints[j])) + 1;j为组成f(i)的最后一枚金币的面值,j可能是数组coins的任意一个值
总结:将凑成总金额i的最少硬币数量设为f(i),假设f(0)、f(1)、f(i-1)已知,则f(i)=min(f(i-coints[j])) + 1;j为组成f(i)的最后一枚金币的面值
代码:
class Solution {public int coinChange(int[] coins, int amount) {//创建一个amount + 1 的数组(因为还需要包含dp[0])int[] dp = new int[amount + 1];
//补充1:为dp[i]赋初值方便min()比较// int top = amount + 1;int top = amount + 1;//补充2:为dp[i]赋初值方便min()比较Arrays.fill(dp,top);dp[0] = 0;
//循环为dp[]赋值,一致赋到dp[amount]for(int i = 1; i <= amount; i++){//f(i) = min(f(i - conins[j]) + 1);i为总金额数for(int j = 0; j < coins.length; j++){//当conins[j] <= i时才相加(如果conins[j] > i,说明conins[j]是无法凑成金额i的,这样可以减少运算量)if(coins[j] <= i){//此时为了进行min()比较,可以为dp[i]都附上初始值,初始值可以选用大于amount的任意值;见补充1、2//注意初始值不可以选用Integer.MAX_VALUE;否则不满足条件时最终判断就是Math.min(MAX_VALUE+1,MAX_VALUE);dp[i] = Math.min(dp[i - coins[j]] + 1,dp[i]);}}}//如果最终的dp[i]还大于amount,说明没有能够组成总金额的硬币,返回-1return dp[amount] > amount ? -1 : dp[amount];}
}3.12 最小路径和(中等):动态规划
题目:给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。说明:每次只能向下或者向右移动一步。
思想:将凑成总金额i的最少硬币数量设为f(i),假设f(0)、f(1)、f(i-1)已知,则f(i)=min(f(i-coints[j])) + 1;j为组成f(i)的最后一枚金币的面值,j可能是数组coins的任意一个值
总结:元素对应的最小路径和与其相邻元素的最小路径和有关,因此可以采用动态规划,具体是:
-
元素对应的最小路径和 = min(上方相邻元素对应的最小路径和,左方相邻元素对应的最小路径和) + 当前元素值
-
设
dp[i][j]表示从左上角出发到[i][j]的最小路径和:有:dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + grid[i][j]
-
-
特殊情况:
-
只有一个点:
dp[0][0] = grid[0][0];第一个数的最小路径和为该数的值 -
只有一行:
i=0,dp[0][j] = dp[0][j-1] + grid[0][j] -
只有一列:
j=0,dp[i][0] = dp[i-1][0] + grid[i][0]
-
代码:
class Solution {public int minPathSum(int[][] grid) {//grid[][]为空、行数为0、列数为0返回0if(grid == null || grid.length == 0 || grid[0].length == 0){return 0;}
//拿到行数int row = grid.length;//拿到列数int column = grid[0].length;
//记dp[i][j]为到达(i,j)时的最小路径和int[][] dp = new int[row][column];
//只有一个点的情况dp[0][0] = grid[0][0];
//只有一行: i = 0for(int j = 1; j < column; j++){dp[0][j] = dp[0][j - 1] + grid[0][j];}
//只有一列:j = 0for(int i = 1; i < row; i++){dp[i][0] = dp[i - 1][0] + grid[i][0];}
//dp[i][j] = min{dp[i-1][j],dp[i][j-1]} + grid[i][j]for(int i = 1; i < row; i++){for(int j = 1; j < column; j++){dp[i][j] = Math.min(dp[i][j-1], dp[i-1][j]) + grid[i][j];}}
return dp[row-1][column-1];}
}3.13 动态规划总结!!!
-
动态:往往这类问题 某一状态的解 是与 该状态的前一个状态有关系;即通过 当前状态的前一状态 能够推出 当前状态
-
规划:在利用 当前状态的前一状态 推出 当前状态 的过程中,可能会出现种种边界情况,在规划时必须将这些边界情况先单独拎出讨论,然后在使用通用方法解决
相关文章:

Dynaminc Programming相关
目录 3.1 最长回文子串(中等):标志位 3.2 最大子数组和(中等):动态规划 3.3 爬楼梯(简单):动态规划 3.4 买卖股票的最佳时机(简单)࿱…...
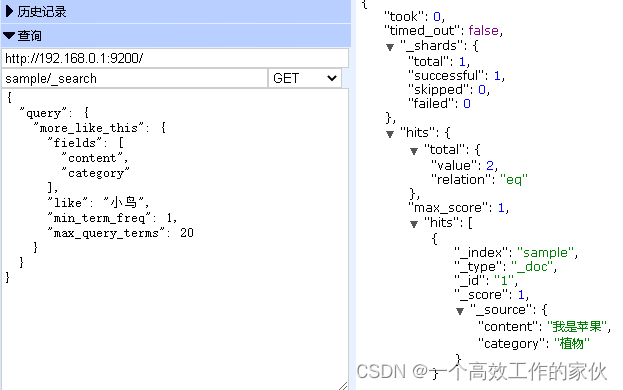
使用 Elasticsearch 轻松进行中文文本分类
本文记录下使用 Elasticsearch 进行文本分类,当我第一次偶然发现 Elasticsearch 时,就被它的易用性、速度和配置选项所吸引。每次使用 Elasticsearch,我都能找到一种更为简单的方法来解决我一贯通过传统的自然语言处理 (NLP) 工具和技术来解决…...

MNN学习笔记(八):使用MNN推理Mediapipe模型
1.项目说明 最近需要用到一些mediapipe中的模型功能,于是尝试对mediapipe中的一些模型进行转换,并使用MNN进行推理;主要模型包括:图像分类、人脸检测及人脸关键点mesh、手掌检测及手势关键点、人体检测及人体关键点、图像嵌入特征…...

主力吸筹指标及其分析和使用说明
文章目录 主力吸筹指标指标代码分析使用说明使用配图主力吸筹指标 VAR1:=REF(LOW,1); VAR2:=SMA(MAX(LOW-VAR1,0),3,1)/SMA(ABS(LOW-VAR1),3,1)*100; VAR3:=EMA(VAR2,3); VAR4:=LLV(LOW,34); VAR5:=HHV(VAR3,34); VAR7:=EMA(IF(LOW<=VAR4,(VAR3+VAR5*2)/2,0),3); /*底线:0,…...
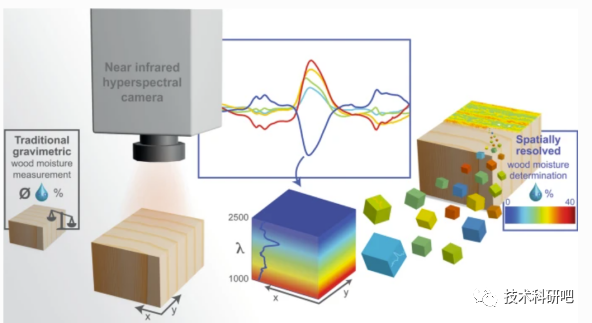
Python高光谱遥感数据处理与高光谱遥感机器学习方法教程
详情点击链接:Python高光谱遥感数据处理与高光谱遥感机器学习方法教程 第一:高光谱基础 一:高光谱遥感基本 01)高光谱遥感 02)光的波长 03)光谱分辨率 04)高光谱遥感的历史和发展 二:高光谱传感器与数据获取 01)高光谱遥感…...
【洛谷】P1678 烦恼的高考志愿
原题链接:https://www.luogu.com.cn/problem/P1678 目录 1. 题目描述 2. 思路分析 3. 代码实现 1. 题目描述 2. 思路分析 将每个学校的分数线用sort()升序排序,再二分查找每个学校的分数线,通过二分找到每个同学估分附近的分数线。 最后…...

开机自启CPU设置定频
sudo apt-get install expect sudo apt-get install cpufrequtils具体步骤如下: 安装 cpufrequtils 工具 ⚫ sudo apt-get install cpufrequtils ⚫ 需要联网下载修改配置文件 ⚫ sudo vi /etc/init.d/cpufrequtils ⚫ 将 GOVERNOR“ondemand” 改为: &g…...
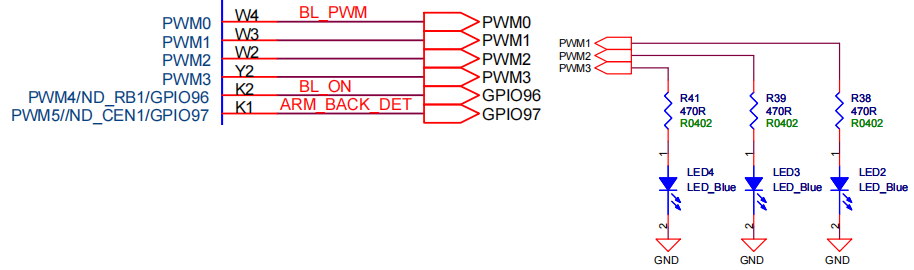
嵌入式Linux开发实操(十二):PWM接口开发
# 前言 使用pwm实现LED点灯,可以说是嵌入式系统的一个基本案例。那么嵌入式linux系统下又如何实现pwm点led灯呢? # PWM在嵌入式linux下的操作指令 实际使用效果如下,可以通过shell指令将开发板对应的LED灯点亮。 点亮3个LED,则分别使用pwm1、pwm2和pwm3。 # PWM引脚的硬…...

消息中间件介绍
消息队列已经逐渐成为企业IT系统内部通信的核心手段。它具有低耦合、可靠投递、广播、流量控制、最终一致性等一系列功能,成为异步RPC的主要手段之一。当今市面上有很多主流的消息中间件,如ActiveMQ、RabbitMQ,Kafka,还有阿里巴巴…...

[Unity] 基础的编程思想, 组件式开发
熟悉 C# 开发的朋友, 在刚进入 Unity 开发时, 不可避免的会有一些迷惑, 例如不清楚 Unity 自己的思想, 如何设计与架构一个应用程序之类的. 本篇文章简要的介绍一下 Unity 的基础编程思想. 独立 Unity 很少使用 C# 的标准库, 例如 C# 的网络, 事件驱动, 对象模型, 这些概念在 …...
SVN 项目管理笔记
SVN 项目管理笔记 主要是介绍 SVN 管理项目的常用操作,方便以后查阅!!! 一、本地项目提交到SVN流程 在SVN仓库下创建和项目名同样的文件夹目录;选中本地项目文件,选择SVN->checkout,第一个是远程仓库项…...

Android获取手机已安装应用列表JAVA实现
最终效果: 设计 实现java代码: //获取包列表private List<String> getPkgList() {List<String> packages new ArrayList<String>();try {//使用命令行方式获取包列表Process p Runtime.getRuntime().exec("pm list packages");//取得命令行输出…...

【校招VIP】有一个比赛获奖项目和参与的开源小项目,秋招项目竞争力够不够?三个标准,自己都可以估算
有个24届的学生问我:现在没有实习,能不能参与大厂秋招?手里有两个项目,一个是比赛的获奖项目,一个是CSDN上博主做的开源小项目,这两个项目竞争力够不够? 其实项目这块,无非就是三个…...

量化开发学习入门-概念篇
1.网格交易法 网格交易法(Grid Trading)是一种基于价格波动和区间震荡的交易策略。它适用于市场处于横盘或震荡的情况下。 网格交易法的基本思想是在设定的价格区间内均匀地建立多个买入和卖出水平(网格),并在价格上…...
以及向量处理)
【草稿】关于文本句子分割(中文+英文)以及向量处理
获取文本 主函数 Main # -*- encoding: utf-8 -*- # Author: SWHL # Contact: liekkaskono163.com from pathlib import Path from typing import Dict, List, Unionimport filetypefrom ..utils import logger from .image_loader import ImageLoader from .office_loader i…...
【瑞吉外卖】所遇问题及解决方法
太菜了实习之余瑞吉外卖补充一下基础知识(,不然真啥也不会了。 请输入正确的手机号! 是因为我测试了我的手机号,爆红,以为方法有错。但其实是前端代码检查手机号是否符合规范的语句有点()啊啊…...

【Hugo入门】基础用法
检查Hugo是否安装 hugo version显示所有可用命令 hugo help显示指定命令的可用子命令,例如查询server的所有子命令 hugo server --help建立你的网站,cd进入你的项目根目录运行 hugo默认发布内容到自动创建的public文件夹。 覆盖hugo或hugo server的默…...

Java实现一个简单的图书管理系统(内有源码)
简介 哈喽哈喽大家好啊,之前作者也是讲了Java不少的知识点了,为了巩固之前的知识点再为了让我们深入Java面向对象这一基本特性,就让我们完成一个图书管理系统的小项目吧。 项目简介:通过管理员和普通用户的两种操作界面࿰…...
网络安全等级保护2.0
等保介绍 信息系统运维安全管理规定(范文)| 资料 等保测评是为了符合国家法律发挥的需求,而不是安全认证(ISO) 一般情况没有高危安全风险一般可以通过,但若发现高位安全风险则一票否决 二级两年一次 三…...
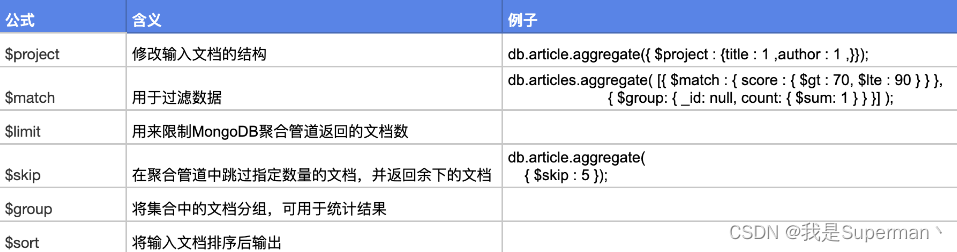
【sql】MongoDB 增删改查 高级用法
【sql】MongoDB 增删改查 高级用法 相关使用文档 MongoDB Query API — MongoDB Manual https://www.mongodb.com/docs/manual/reference/sql-comparison //增 //新增数据2种方式 db.msg.save({"name":"springboot😀"}); db.msg.insert({&qu…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...
